非参数回归的贝叶斯估计

苏雅玲,何幼桦

(上海大学理学院,上海200444)

在回归分析中,相对于回归函数形式已知的参数回归,非参数回归的函数形式自由,受约束少,回归模型完全由数据驱动.对于非参数回归问题,已经有很多学者进行了研究,目前回归函数的非参数估计主要集中在核估计、局部多项式估计、样条函数以及小波估计.如Devroye[1]证明了回归函数核估计的强相合性.Greblicki等[2]和Devroye[3]在不同条件下证明了回归函数核估计的逐点相合性.Fan[4]引入局部线性回归估计并阐述其优越性,给出了估计量的均方误差(mean-square error,MSE)和积分均方误差(mean integrated square error,MISE),并研究了估计量的最大最小效.Antoniadis等[5]引入回归函数的小波估计,并证明了估计量的相合性和渐进正态性.上述方法单纯从数据本身出发,没有充分利用数据以外的信息,虽然能够达到较好的拟合效果,但是外推效果较差.

在参数估计问题中,贝叶斯方法已经得到广泛的应用,而在非参数估计问题中,贝叶斯方法是从Ferguson[6]在1973年发表了论文A Bayesian Analysis of Some Nonparametric Problems[6]后才开始受到关注.Ferguson给出了当总体X 的分布函数F(x)的先验为Dirichlet过程时,F(x)的非参数贝叶斯估计为F(x)先验分布与经验分布的加权平均.此外,Jayaram[7]提出了拓展的Dirichlet过程先验.在此基础上姚宗静[8]给出简单Dirichlet过程的构造性定义,讨论了其性质和支撑问题,求出在该先验下后验分布的具体表达形式.也有学者将非参数贝叶斯方法应用到回归函数的估计中,如龙杏芬等[9]在局部线性估计中窗宽h的先验分布为Gamma分布的条件下,基于贝叶斯方法构造了回归函数的局部线性估计,并给出窗宽和回归函数的后验分布和抽样方法,通过数值模拟验证了贝叶斯局部线性估计方法的可行性.卢一强等[10]对广义非参数模型B样条贝叶斯估计进行了研究,给出了回归函数B样条贝叶斯估计的马尔科夫链蒙特卡洛(Markov chain Monte Carlo,MCMC)模拟计算方法.

本工作针对非参数回归模型,在Ferguson给出的总体分布函数的贝叶斯估计基础上,进一步得到一个光滑的条件分布估计.基于该分布最终构造出回归函数的贝叶斯估计,并研究该估计的收敛性质,给出该估计中超参数的合理表达式.最后,通过实证分析将非参数贝叶斯方法与局部线性回归进行了比较.

1 非参数回归的贝叶斯估计

文献[6]给出了总体X的分布函数F(x)的非参数贝叶斯估计,在该估计中取F(x)的先验分布服从Dirichlet过程.Dirichlet过程定义如下.

定义1 设X为一样本空间,A是X的子集构成的σ代数,α＞0,P0为(X,A)上的有限非零测度.如果对 X 的任意可测分割 A1,A2,···,Am,p=(P(A1),P(A2),···,P(Am))服从参数为α =(αP0(A1),αP0(A2),···,αP0(Am)) 的 Dirichlet分布,则称p是(X,A)上参数为 α,基测度为P0的Dirichlet过程,记为p～DP(α,P0).

文献[6]中的Dirichlet过程即为DP(α,P0),α为正实数,记F0(x)=P0{X ≤x}是先验过程的期望(均值函数).则在样本为x1,x2,···,xn时,F(x)的贝叶斯估计为

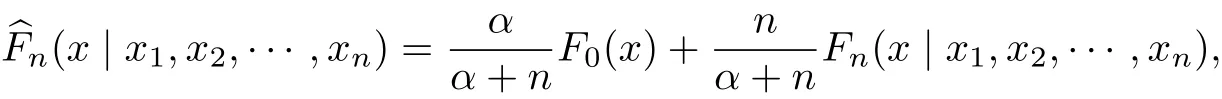
该估计是先验过程的期望分布F0(x)和经验分布估计Fn(x|x1,x2,···,xn)的加权平均.由于经验分布函数是阶梯函数,为得到一个光滑的分布估计,用核估计代替经验分布函数Fn(x|x1,x2,···,xn),则总体的密度估计为

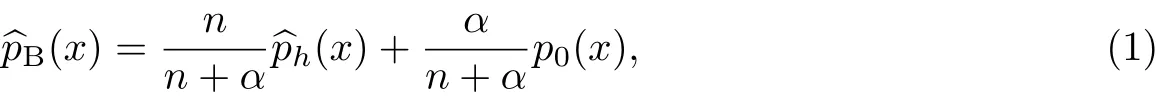
现考虑Y∈R1对X=(X1,X2,···,Xd)∈Rd的多元非参数回归模型

其中m(X)是未知回归函数,ε是均值为0方差为σ2的误差项.设(x,y)是变量(X,Y)的某个具体取值,{(Xi,Yi),i=1,2,···,n}为样本数据.在多维情况下,式(1)可表示成如下形式:

Y的条件分布的贝叶斯估计为

在二次损失下,回归函数m(x)的贝叶斯估计为

式中,m0(x)为m(x)基于p0(x,y)的先验回归函数Nadaraya-Watson核回归估计,即零阶局部多项式回归.考虑一阶局部多项式回归(局部线性回归)将会减少边界偏倚,而不增加方差[11],因此在计算中可以将式(3)中的多元Nadaraya-Watson核回归估计 ^mH(x)替换成多元局部线性回归估计

另一方面,m(x)的贝叶斯估计式(3)中,α反映 ^mB(x)对先验m0(x)的依赖程度,如果这种依赖随x的变化而有所不同,则式(3)可写成

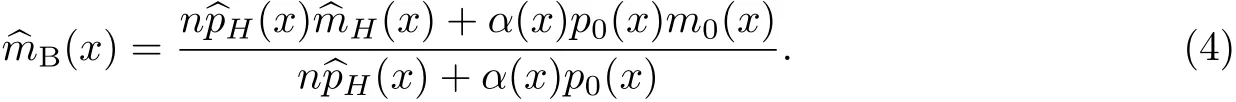
1.1 估计的均方收敛性

文献[12]给出了多元局部线性回归估计 ^mH(x)的方差和偏差.

引理 1 对于样本模型Yi=m(Xi)+εi,i=1,2,···,n.^mH(x)为m(x)具有带宽矩阵H的局部线性估计,并满足文献[13]中的正则条件.设x为一个非边界点,则在给定X1,X2,···,Xn下^mH的偏倚为

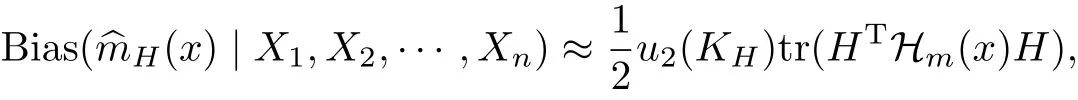
这里Hm(x)为m(x)的Hessian矩阵,而u2(KH)是核函数KH的二阶矩.^mH的方差为

记Var(^mH(x))=Vn(x),Bias(^mH(x))=E(^mH(x))-m(x)=Bn(x),则m(x)核估计^mH(x)的均方误差为

定理1 在^mH(x)满足引理1的条件下,m(x)的贝叶斯估计的均方误差为

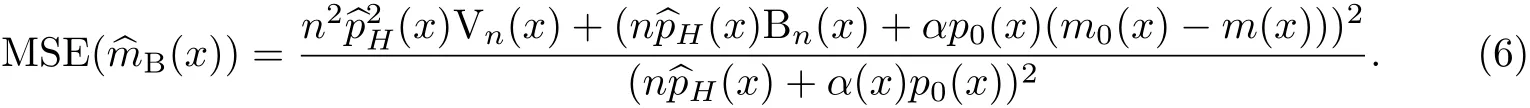
注意到,当m0(x)=m(x)时,

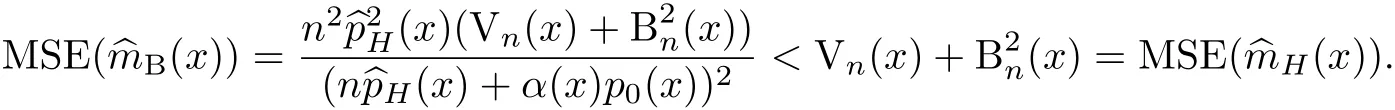
由此可知,当m(x)先验选择接近m(x)时,m(x)的非参数贝叶斯估计的均方误差将小于其局部线性回归估计的均方误差.

1.2 超参数α(x)的确定

式(4)中的超参数α(x)反映了分布估计对先验分布的依赖程度,α(x)越大则这种依赖越强.在实际计算时,需要对超参数α(x)进行合理地确定.

定理2 以MSE达到最小的α(x)可以表示为

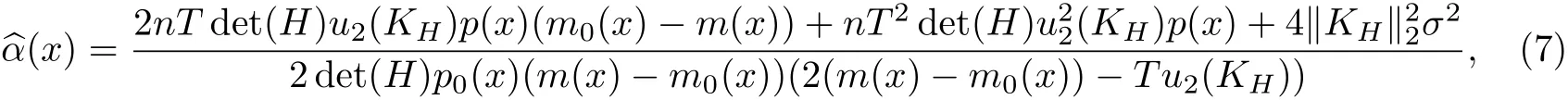
其中T=tr(HTHm(x)H).

证明

其中

上述约等式中是用p(x)代替了核估计^pH(x).

MSE(^mB(x))关于α(x)的一阶偏导数为

得式(7)的结果.又因α(x)为式(7)时

所以当α(x)取式(7)时,MSE(^mB(x))取得极小值.

在定理2中,当m(x)对每个分量的二阶偏导接近0,即T≈0时,则可取

根据式(8)可知,当先验回归函数的选取和真实的回归函数接近时,(m(x)-m0(x))2较小,^α(x)较大,回归函数的非参数贝叶斯估计结果对先验分布依赖度高.反之,当先验回归函数的选取和真实的回归函数相差较大时,^α(x)较小,则估计结果对先验分布依赖度较低.由于m(x)是未知的,先验m0(x)的选取具有主观性,因此可以限定(m(x)-m0(x))2≤M,M为正实数.式(8)中α(x)的确定还依赖方差σ2,其估计可采用文献[11]中的方法.

2 实证分析

为了检验所提出算法的有效性,本工作以人口预测问题作为实证分析,样本选取1990—2005年的中国人口数据,建立人口数量对时间的回归模型,运用非参数贝叶斯方法对模型进行估计,最后以2006—2010年的数据检验模型,并将结果与局部线性回归进行对比分析.

2.1 人口模型的估计

基于1990—2005年的中国人口样本建立一元非参数回归模型:

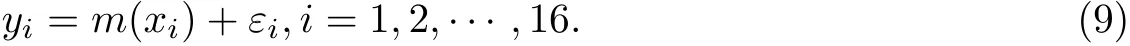
选取Logistics人口模型[14]作为先验:

表1 1990—2005年中国人口数量估计结果Table 1 Estimation of China's population in 1990—2005 万人

表2 拟合均方误差MSETable 2 Fitting mean square error MSE万人

由表2可以看出,非参数贝叶斯估计与局部线性回归方法相比较,均方误差要小得多,拟合效果较好.

2.2 人口模型的预测

由2.1节得到人口数量的非参数贝叶斯估计结果,预测2006—2010年中国人口数量如表3所示.表4为预测均方误差.表4表明在对中国人口数量进行预测时,非参数贝叶斯估计与局部线性回归相比较,均方误差较小,在一定程度上克服了局部线性回归方法在预测外推方面效果较差的问题.

表3 2006—2010年中国人口数量预测结果Table 3 China's population forcast results from 2006 to 2010 万人

表4 预测均方误差MSETable 4 Prediction mean square error MSE 万人

3 结束语

本工作利用Y对X的条件分布的非参数贝叶斯估计来构造回归函数的非参数贝叶斯估计,在此过程中,用分布估计的核估计替代Ferguson估计的经验分布函数,用较高阶的局部多项式回归替代原构造中的Nadaraya-Watson回归估计,获得了较为理想的估计效果,同时还给出了估计的均方误差及其均方收敛性.实证结果表明,对于非参数贝叶斯估计,当先验分布选择较合适时,在数据拟合和预测方面均表现出了较好的效果.