尖底摆动从动件圆盘凸轮的设计及特性值分析

黄小平，郑梅生

(南京林业大学 机械电子工程学院，江苏 南京 210037)

0 引言

为了满足实际应用的某些特定要求和具备优良性能，同时考虑到便于加工和检测、提高制造和测量的精度、减少成本、避免依赖高档高精度加工设备等方面，工程中广泛采用一类廓线形状简单的平面盘形凸轮(以下简称为简单廓线凸轮)，其廓线是圆弧、直线、渐开线、椭圆、阿基米德螺线、对数螺旋等曲线或它们的组合[1～11]。其中，圆盘凸轮(又称单圆弧盘形凸轮[12])的廓线是圆，形状最简单，制造和测量最容易。充分研究简单廓线凸轮机构的运动和动力特性，确定其适用场合，促进其更多应用，具有显著的学术意义和经济价值。

众所周知，从动件的运动规律与凸轮的理论廓线(以下简称为凸轮廓线)相对应。凸轮廓线种类不同，则从动件运动规律种类不同，从动件的速度最值、加速度最值、跃度最值和作用于凸轮上的阻力矩最值等随之不同，从而凸轮机构的工作性能不同。这些最值若以无量纲形式表示，即为从动件运动规律的特性值[13-14](以下简称为特性值)。这些特性值从不同角度反映从动件运动规律(凸轮廓线种类)对机构动力学性能的影响，和压力角、机械效率一起，构成机构动力学性能的多种评价指标，其数值大小是确定各种运动规律(凸轮廓线)适用于什么工作场合(低、中、高速度，轻、中、重载荷)的主要依据[13-15]。文献[13-15]给出了常用运动规律，例如等速、等加速、等减速、简谐等运动规律的特性值。而简单廓线凸轮的特性值研究，经国内外资料检索，几乎还未开展，仅见有文献[12]针对对心直动从动件圆盘凸轮的涉及从动件位移1、2阶导数的近似分析和近似数据，因而这一大类凸轮机构还没像人们所熟知的采用各种常用运动规律的一大类凸轮机构那样，能从特性值方面进行动力学性能的评判，而确定其最适用场合。此外在现有文献中，有关圆盘凸轮机构设计方法的内容也很少见到，这将影响该种机构的良好设计和应用。

作为改变此现状的初步探索，本文研究尖底(或滚子)摆动从动件圆盘凸轮的运动学、压力角、上述4个主要特性值以及设计方法，为丰富其设计校核和性能评价提供理论依据。

将滚子从动件的滚子中心视为尖底从动件的尖底，则滚子从动件的凸轮机构即成为尖底从动件的凸轮机构，因此文中仅研究后者。

1 机构的构形、坐标系及参数定义

将不同的圆盘凸轮转向(顺时针或反时针方向)与尖底摆动从动件相对于圆盘凸轮的不同初始位置进行组合，可形成该机构的多种情况。通过将机构整体在其所在平面内转动某一角度、绕水平轴或竖直轴作180翻转等变换，总可归结为凸轮顺时针转动且从动件初始位置A0B0在机架OA0的上方(图1(a))或下方(图1(b))这两种情形。

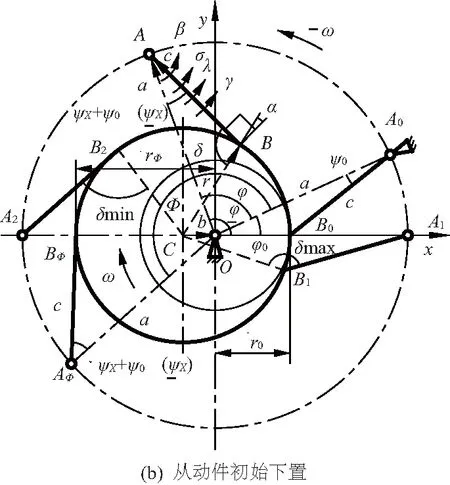
图1 尖底摆动从动件圆盘凸轮

图1中建立固联于圆盘凸轮的右手直角坐标系Oxy，取原点O在凸轮轴心处，坐标轴x通过点O和凸轮圆心C，点C到O的方向为轴x的正向，轴x绕点O反时针转过90得坐标轴y。

设凸轮是原动件，顺时针转动，转角为φ，推程开始时φ= 0，角速度ω为常数，其廓线半径、偏心距(点C和O的距离)为r、b，廓线的最小向径(即基圆半径)、最大向径为r0、rΦ，推程运动角、回程运动角为Φ、Φ'，廓线上的任意点B的直角坐标为(x, y)。

设从动件的长度、转角、初位角、角行程为c、ψ、ψ0、ψx(即ψ的最大值ψmax)，角速度、角加速度、角跃度、角跳度为γ、λ、σ、β。

设机架的长度、初位角为a、φ0。

采用反转法研究机构运动，即给整个机构一个绕点O且角速度为(-ω)的反转运动，于是凸轮固定不动，从动件AB在跟随机架OA反转(这时机架相对凸轮转过的角度即为原来凸轮相对机架转过的角度φ)的同时，还相对机架以原来运动规律ψ= ψ(φ)运动。

简记角φ的三角函数sinφ、cosφ为sφ、cφ(其他角的三角函数也这样简记)，反三角函数arccos、arctan为c-1、t-1。

对φ的1、2、3、4阶导数d/dφ、d2/dφ2、d3/dφ3、d4/dφ4简记为上标9、、、。

2 尺寸常数

由图1的△OA0B0、△OAΦBΦ和余弦定理有：

(1)

其中：b>0，a>0，c>0，r>0。

众所周知，机构各构件转角之间关系只取决于各构件相对长度。引入长度比例系数mb(称为凸轮偏心率)、ma和mc：

(2)

则：

(3)

其中：mb>0，ma>0，mc>0。

显然，机构全部尺寸常数中4个独立(例如r、b、a、c)，已知任意4个尺寸常数，可由式(1)-式(3)求出其他尺寸常数。

3 凸轮廓线方程

记φ= φ-φ0(图1(a))，φ=φ+φ0(图1(b))，ψ= ψ+ ψ0(图1)，则：

φ=φ∓φ0ψ=ψ+ψ0φ′=1ψ′=ψ′(ψ∓φ)′=ψ′∓1

(4)

式(4)中的第1和第5式的“∓”号，其上方符号对应图1(a)机构、下方符号对应图1(b)机构，下同，不再赘述，但特别指出的除外。

在图1四边形OABC中，矢量a、c与x轴正向的夹角为φ、φ-ψ(图1(a))或φ+ψ(图1(b))。将矢量OB= a- c在x、y轴上投影，有x= acφ- ccφ±ψ，y= asφ- csφ±ψ，注意到φ∓ψ=∓(ψ∓φ)，得凸轮廓线方程：

(5)

4 行程速比系数和从动件运动规律

显然，圆盘凸轮机构中从动件运动为“升-降”型，无休止(停留)阶段。

凸轮是原动件，故机构的行程速比系数K=从动件慢行程凸轮运动角/从动件快行程凸轮运动角。因Φ9= 2π- Φ，故若Φ<180，则从动件的推程是快行程，回程是慢行程，K= Φ9 /Φ= 2π/Φ- 1；若Φ>180，则从动件的推程是慢行程，回程是快行程，K=Φ/Φ9=1/(2π/Φ-1)。

将图1的四边形OABC中的矢量等式r= b+ a- c的两边作自身的点积(数量积)有：rr= bb+ aa+ cc+ 2(ba- bc- ac)，即r2= b2+ a2+ c2+ 2(bacφ- bccφ∓ψ- accψ)，[(b2+ a2+ c2- r2)/ 2+ bacφ] /c= acψ+ bcψ∓φ，

[(mb2+ ma2+ mc2- 1)/2+ mbmacφ]/mc= macψ+mbcψ∓φ= macψ+ mb(cφcψsφsψ)

(a)

记：

(6)

则：

Dsψ+ Ecψ= F，

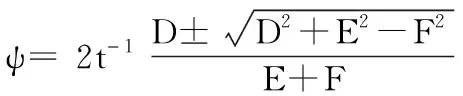
(7)

从文献[13-14]知：

(8)

记P= sψ/mb，Q= sψ∓φ/ma，R= sφ/mc，则：

P9= cψψ9/mb，P"= (cψψ- sψψ92)/mb，P= (cψψ- 3sψψ9ψ- cψψ93)/mb，

Q9= cψ∓φ(ψ9∓1)/ma，Q"= [cψ∓φψ"- sψ∓φ(ψ9∓1)2]/ma，Q= [cψ∓φψ- 3sψ∓φ(ψ9∓1)ψ- cψ∓φ(ψ9∓1)3]/ma，

R9= cφ/mc，R"= - sφ/mc，R= - cφ/mc。

由式(a)有cψ/mb+ cψ∓φ/ma= [(mb2+ ma2+ mc2- 1)/(2mbma)+ cφ]/mc，对φ求导得sψψ9/mb+ sψ∓φ(ψ9∓1)/ma= sφ/mc。

即(sψ/mb+ sψ∓φ/ma)ψ9=sψ∓φ/ma+ sφ/mc，(P+ Q)ψ9=Q+ R，该式对φ求1、2、3阶导数得：

其中：

- 2[cψψ9/mb+ cψ∓φ(ψ9∓1)/ma]ψ- (cψψ- sψψ92)ψ9/mb- [cψ∓φψ- sψ∓φ(ψ9∓1)2](ψ9∓1)/ma=

- (3cψψ- sψψ92)ψ9/mb- [3cψ∓φψ- sψ∓φ(ψ9∓1)2](ψ9∓1)/ma，

- 3[cψψ9/mb+ cψ∓φ(ψ9∓1)/ma]ψ- 3{(cψψ- sψψ92)/mb+ [cψ∓φψ- sψ∓φ(ψ9∓1)2]/ma}ψ- (cψψ- 3sψψ9ψ- cψψ93)ψ9/mb-[cψ∓φψ- 3sψ∓φ(ψ9∓1)ψ- cψ∓φ(ψ9∓1)3](ψ9∓1)/ma=

- (4cψψ9ψ+ 3cψψ2- 6sψψ92ψ- cψψ94)/mb- [4cψ∓φ(ψ9∓1)ψ+ 3cψ∓φψ2- 6sψ∓φ(ψ9∓1)2ψ- cψ∓φ(ψ9∓1)4]/ma

故得：

(9)

式(6)、式(7)、式(9)即为从动件运动规律。另外简记：

(10)

从式(2)-式(4)、式(6)、式(7)、式(9)、式(10)知ψ、ψ9、ψ、ψ、ψ、μ、μ9由常数mb、ma、mc和变量φ决定，都无量纲。

5 压力角

压力角是机构传动质量的重要指标，在设计中必不可少，下面研究图1机构的压力角α。

5.1 压力角计算式

(11)

5.2 压力角最大值及出现位置

由式(11)第2式知，α的最大值αmax=max{90- δmin，δmax- 90}，其中δmin、δmax是δ的最小值、最大值。若简记

α1=δmax-90° α2=90°-δminφ1=±φ0φ2=180°±φ0

(12)

则：

αmax=max{α1，α2}

(13)

由式(4)第1式、式(11)、式(12)、以及图1的△OA1B1、△OA2B2知，当φ为φ1、φ2时，φ为0、180，δ为δmax、δmin，α为α1、α2，注意到式(13)即知φ1、φ2是αmax可能出现位置。

由式(12)、式(11)有：

(14)

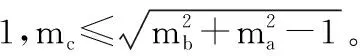
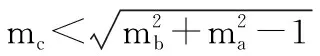
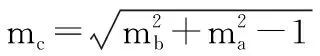
φ1、φ2由式(12)第3、4式和式(12)第1式确定，α1、α2由式(14)确定。

5.3 压力角约束

保证机构良好传动需满足的条件为：

αmax≤[α]

(15)

其中[α]是许用压力角。δmax、δmin的最大可取值区间是[0,180]，由式(12)前2式知α1、α2的最大可取值区间是[-90,90]，由式(13)、式(15)有

sαmax=max{sα1，sα2}≤s[α]，即sα1≤s[α]和sα2≤s[α]

(16)

式(14)第1式代入sα1≤s[α]有(ma+ mb)2≤mc2+ 2mcs[α]+ 1；式(14)第2式代入sα2≤s[α]有(ma- mb)2≥mc2- 2mcs[α]+ 1。于是得：

(ma+ mb)2- (mc+ s[α])2≤c[α]2≤(ma- mb)2- (mc- s[α])2

(17)

式(17)即是图1机构压力角约束的表达式。

6 特性值

文献[13-14]指出：直动从动件凸轮机构在一个行程(推程或回程)中的无量纲速度、无量纲加速度、无量纲跃度、无量纲转矩的计算式依次为s9Θ /h、sΘ2/h、sΘ3/h、s9sΘ3/h2，这里的s9、s、s为从动件的类速度、类加速度、类跃度，Θ、h为凸轮运动角、从动件行程；这4个无量纲物理量分别正比于从动件系统的动量、惯性力、惯性力的变化率、凸轮上平衡从动件系统的惯性力所需输入转矩；称这些物理量各自的最小值和最大值，以及各自绝对值的最大值(分别称为最大无量纲速度、最大无量纲加速度、最大无量纲跃度、最大无量纲转矩)为特性值；特性值是评价从动件运动规律的优劣和适用场合的动力学特性指标，其绝对值都越小越好。对摆动从动件，上面的线量要换成角量。

圆盘凸轮机构的一个运动循环由首尾相接的一个推程和一个回程所组成。在图1所示机构的推程和回程，从动件角行程ψx相等但凸轮运动角不等(Φ≠Φ9)，故其无量纲角速度Γ、无量纲角加速度Λ、无量纲角跃度Σ、无量纲转矩T的公式要按推程和回程分别写出，为:

(18)

由节2和节4易知Γ、Λ、Σ、T由常量mb、ma、mc和变量φ决定。Φ、Φ9、ψx都为正值，而ψ9、ψ、ψ、μ在一个运动循环中都既有正值也有负值(参见图2)，再从式(18)知Γ、Λ、Σ、T在一个运动循环中的最小值为负、最大值为正。

(19)

7 解析法设计计算流程

首先给定r、mb、Φ、ψx、[α]值，其次按以下公式和顺序作设计计算：

1) 在满足ma>0、mc>0、(ma+ mb)2- (mc+ s[α])2≤c[α]2≤(ma- mb)2-(mc- s[α])2等约束下，联立式(3)的4个等式即

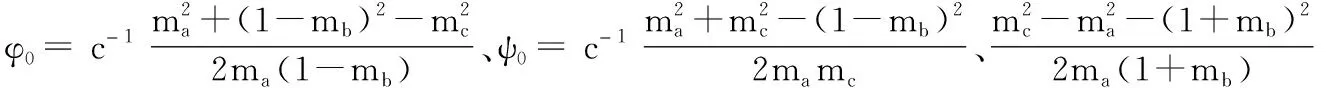
(例如，设mb= 0.3，Φ= 175，ψx= 15，[α]= 40，利用软件Excel的规划求解功能，可这样求得ma= 2.508，mc= 2.194，φ0= 56.0，ψ0= 15.3。

2) 计算b= mbr，a= mar，c= mcr。以φ为自变量，按式(6)和式(7)计算D、E、F、ψ，按式(5)计算x、y，按式(9)和式(10)计算ψ9、ψ、ψ、ψ、μ、μ9，按式(11)计算δ、α，按节6末尾所述方法计算Γm、Λm、Σm、Tm等。

8 计算实例

为验证本文导出公式的正确性并获得有设计指导意义的结论，取若干组mb和ma值，按节7的步骤做计算绘图，得从动件运动线图(见图2，其中ψ的单位为弧度，ψ9、ψ、ψ、ψ、μ、μ9均无量纲)以及图1所示机构的特性值(见表1，其中Γm、Λm、Σ：m、Tm均无量纲)。

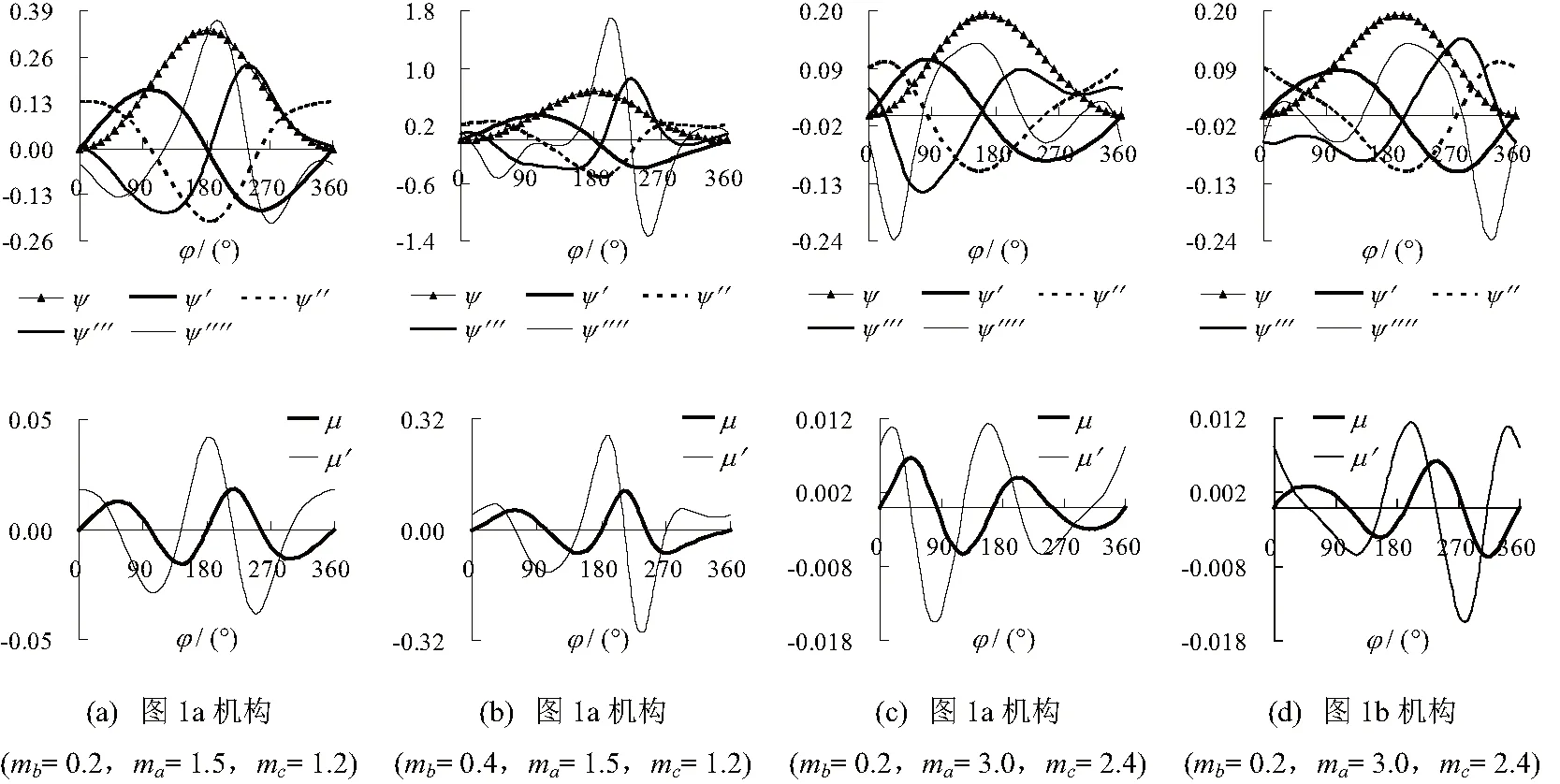
图2 从动件运动线图

长度比例系数特性值mbmamcΓmΛmΣmTm0.11.51.21.585.5217.24.300.21.51.21.626.1621.44.960.31.51.21.686.7328.15.960.13.02.41.605.5417.24.120.23.02.41.636.2418.74.420.33.02.41.637.0829.35.15

9 结论分析

1) 与采用各种常用运动规律的凸轮机构的设计不同，尖底摆动从动件圆盘凸轮机构的一些未知参数需要在满足尺寸参数和压力角的约束下通过求解非线性方程组来确定(见节7的步骤1))。

2) αmax、Γm、Λm、Σm、Tm等这些表征机构动力学性能的指标，仅由机构长度尺寸的相对值(本文中为mb、ma、mc)决定(节5.2和节6)。

3) 凸轮偏心率mb越大，则ψ、ψ、ψ、μ的最大绝对值越大(图2和表1)，γ、λ、σ、β的最大绝对值越大(式(8)和式(18))，Γm、Λm、Σm、Tm的值越大(式(19))，从而机构动力学性能越差。因此mb值不宜过大。

4) 在相同尺寸情况下，图1(a)、图1(b)两机构的运动线图之间具有对称性(见图2(c)和图2(d))：ψ对φ的偶数阶导数ψ、ψ、ψ曲线以及μ曲线都对称于竖直线φ=180，奇数阶导数ψ、ψ曲线以及μ曲线都对称于φ轴上的点φ=180。利用这些对称性，若已知其中一机构的运动线图，极易得到另一机构的运动线图。

5) 由于圆盘凸轮的廓线是完整的单一圆周，故从动件转角ψ对凸轮转角φ的任意阶导数的曲线均连续且光滑(参见图2)，即机构无任意阶导数不连续而发生的冲击，性能上必优于大多数的从动件常用运动规律，例如等加速等减速、负等跃度、正等跃度、摆线等运动规律(因从动件位移对凸轮位移的某低阶或高阶导数不连续而存在冲击)。再由圆盘凸轮的廓线极易制造和检测的特点即知，在从动件运动是“升-降”型、对从动件运动规律无特别要求、考虑制造和动力学两方面的综合表现的情况下，圆盘凸轮机构是最好的凸轮机构，可用于高速场合，值得重视和尽量采用。

10 结语

相对现有文献，本文的主要特点是：1) 首次研究了偏置直动从动件圆盘凸轮的特性值问题，为其他简单廓线凸轮机构的特性值研究提供了借鉴；2) 运用恰当的方法和表达技巧，推导出该机构从动件位移的0-4阶导数的精确且简洁的公式，解决了确定该凸轮机构特性值需要从动件位移的3、4阶高阶导数公式的关键难题；3) 给出该机构4个主要特性值的公式。据其数值计算结果，可判断该机构与特性值有关的动力学性能的优劣和适用场合；4) 得出该机构特性值只和各构件的相对长度有关，以及该机构可用于高速的结论；5) 详细研究了机构压力角，给出在满足压力角和尺寸的约束下通过求解非线性方程组来确定机构尺寸的一种方法和实例。