基于刚柔耦合的无油涡旋压缩机小曲拐动力特性分析
彭斌,方圆力,朱永军
(兰州理工大学 机电工程学院,甘肃 兰州 730050)
0 引言
无油涡旋压缩机作为最新一代的容积式压缩机,具有可靠性高、结构简单、噪声小、振动低、效率高的特点。传统多体系统动力学的研究主要局限于刚体领域,随着现代机械向高精度、高速度以及高效率的方向发展,纯刚性假设已很难满足某些条件下的精度要求。因此系统自身的刚性运动与系统自身的变形耦合产生的弹性力学问题逐渐成为当代研究的热点。无油涡旋压缩机是一种高速运转的机械,仅仅依靠纯刚体系统无法完全体现涡旋压缩机准确的运动状况。作用在动盘上的切向力会使动盘产生绕主轴偏心线转动的自转力矩,使动、静盘不能正常啮合,在设计中往往需要采用防自转机构来限制此自转力矩。无油涡旋压缩机采用小曲拐作为防自转机构,其动力特性将直接关系到防自转机构能否很好地平衡自转力矩[1-2]。
余洋通过模拟仿真得出了运动间隙对动态特性的影响[3];张春、黄华军等人建立了刚柔耦合仿真模型,对转子系统轴承进行了力学分析[4];邵兵通过对涡旋压缩机整机的仿真分析,得出了气体力对整机泄漏的影响[5]。彭斌等对无油涡旋压缩机的前景进行了展望[6],王志军利用三维软件对实际运动进行了仿真,并对实际运动与理论运动进行了比对分析[7]。
因此,小曲拐作为涡旋压缩机高速运转的零件,其动力特性的研究具有重要的意义。本文通过Ansys与Adams的联合仿真,建立了涡旋压缩机小曲拐的刚柔耦合模型,并对其进行了仿真分析,得到的结果将对小曲拐的优化提供重要的依据。
1 小曲拐的机构模型
图1所示为小曲拐装配图。3个小曲拐两端的轴颈分别插在动盘与机架中。
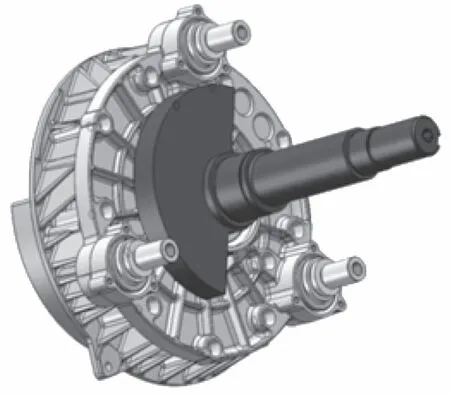
图1 小曲拐装配图
图2所示为小曲拐四杆机构模型,其中1为连接电动机的偏心主轴,3、4、5为3个小曲拐,6为机架,2为连接偏心主轴与小曲拐的动盘。机构有5个活动构件,8个旋转副,其中有2个虚约束,则需要去掉虚约束,由此得到的机构的自由度计算公式为:
F=3n-(2p1+Ph)=3×3-(2×4+0)=1
(1)
其自由度为1,保证了小曲拐的正常运动,从小曲拐四杆机构可以看出3个小曲拐的运动规律一致,且与偏心主轴的运动一致,使得动盘公转运动而不发生自转,因此满足涡旋压缩机防自转的要求。
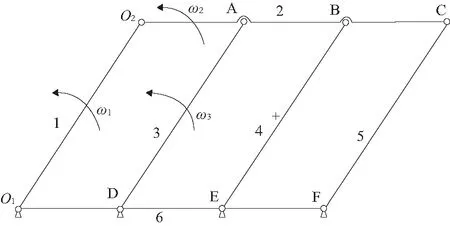
图2 小曲拐四杆机构模型
2 柔性化理论
Adams柔性体所用的理论为柔性化理论,柔性体的坐标系如图3所示,包括动坐标系ed以及惯性坐标系er。动坐标系是为了研究柔性体而建立的坐标系。惯性坐标系相当于大地坐标系,它不会随时间的变化而变化,而动坐标系可以相对于惯性坐标系在一定范围内移动与转动,动坐标系在惯性坐标系中的坐标则被称为参考坐标系[8]。

图3 柔性体节点坐标
对于柔性体上的任意一点p,其位置向量为:
(2)

柔性体中的任一节点采用模态(模态为一个构件的固有属性)坐标的方式来表示变形:
(3)
式中:φp为p点的里兹基向量变形的模态矩阵;qf为广义坐标系。
3 刚柔耦合模型的建立
3.1 MNF文件的建立
利用SolidWorks建立小曲拐的三维模型,通过parasolid通用格式导入到Ansys中建立涡旋压缩机的虚拟样机模型,建立的虚拟样机模型如图4所示。

图4 虚拟样机模型
定义小曲拐的材料属性,弹性模量为210GPa,泊松比0.3,密度7.8×103kg/m3,定义单元类型为solid187格式,最后进行网格的划分。由于小曲拐前后轴颈都插在轴承中,因此,在小轴的轴颈部分建立刚性区域,建立的有限元模型如图5所示,最后将生成的MNF文件导出,模型节点数为14 791,单元数为77 850。

图5 小曲拐有限元模型
3.2 约束与驱动的添加
Bushing轴套力是通过一种数学模型的方式,利用软件设置弹性和阻尼来模拟几个零件之间的连接关系,通过设置Bushing径向刚度、轴向刚度和角刚度的数值来模拟轴承。由于轴承的阻尼很小,因此在本章中忽略不计。根据轴承类型选取位移刚度数值为Kx=1.84e5、Ky=1.84e5、Kz=2.6e5,选取的角度刚度数值为Kxx=1.4e5、Kyy=1.4e5、Kzz=0[9]。
在涡旋压缩机虚拟样机模型建立之后,通过各零件之间关系对涡旋压缩机各个零件添加约束关系及驱动,按电动机的额定转速设置主轴的转速为1 440r/min。各个零件之间的约束如表1所示[10]。
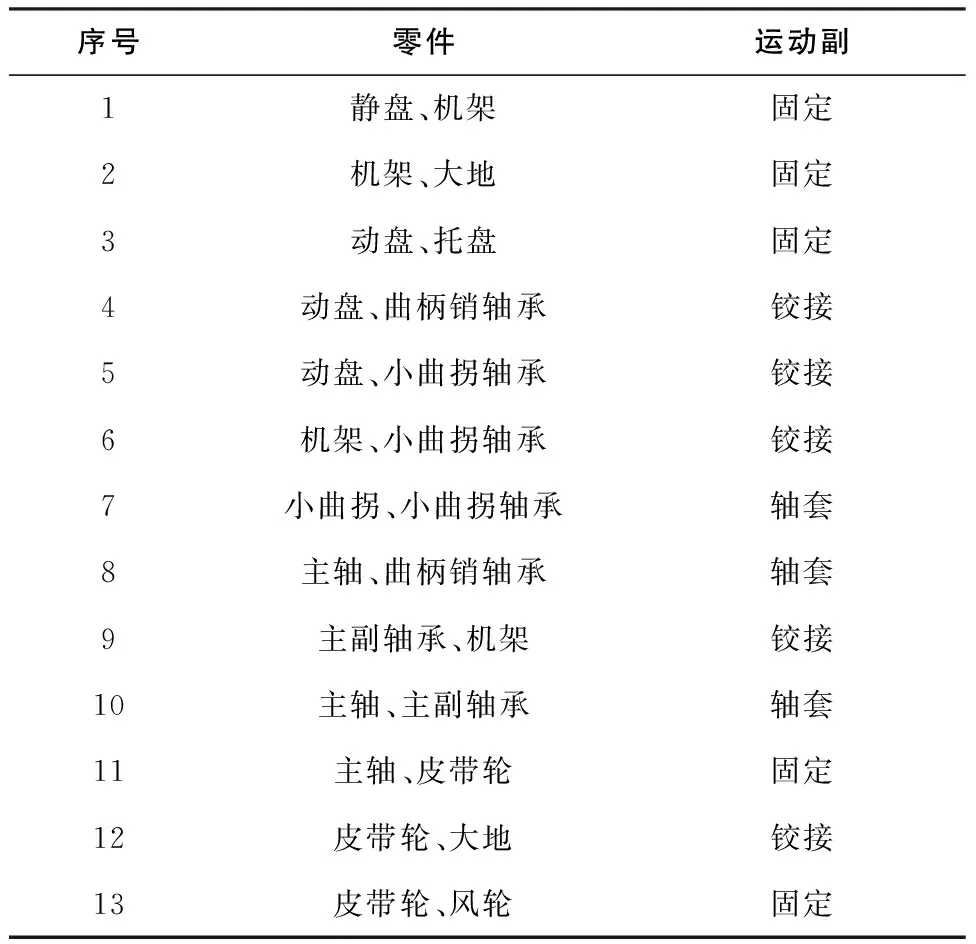
表1 涡旋压缩机刚柔耦合模型各零件间关系
3.3 虚拟样机的装配
在Adams中,根据上面的各零件之间的关系进行涡旋压缩机的刚柔耦合模型的虚拟装配,导入MNF文件进行柔性体的替换。图6为柔性体替换示意图。
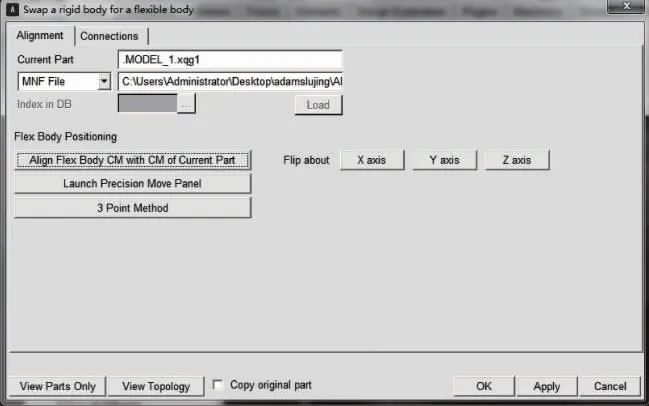
图6 柔性体替换示意图
4 刚柔耦合仿真分析
在Adams中添加Adams/Durability模块,在此模块中可以分析得出柔性体任意时刻的动态特性,也可查看柔性体上任意一个节点的应力应变随主轴转角的变化趋势。
如图7-图9所示的是涡旋压缩机3个小曲拐在主轴旋转一周的工作状况下,10个最大节点的应力值。由图中看出,最大的应力前7个节点是相同的,由此可知,涡旋压缩机3个小曲拐的受力情况、运动状态基本相同,符合小曲拐平面四杆机构的运动规律。

图7 小曲拐1 10个最大应力点
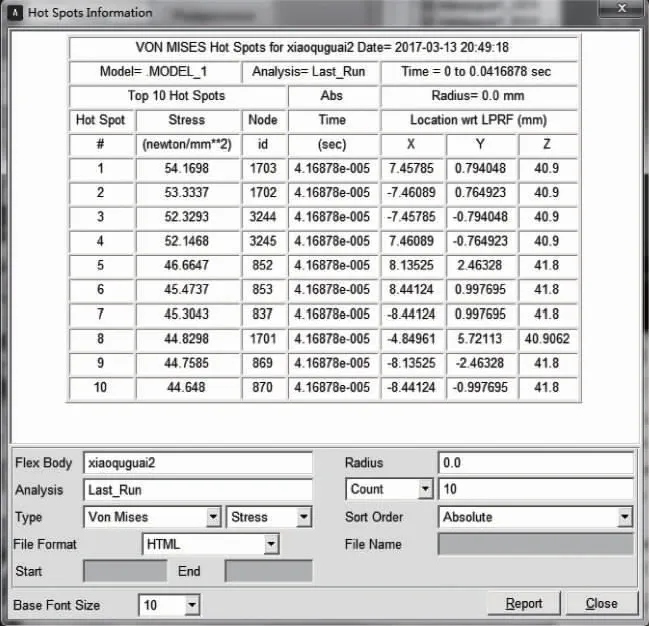
图8 小曲拐2 10个最大应力点

图9 小曲拐3 10个最大应力点
图10-图12所示为3个小曲拐应力应变的等值云图。小曲拐两端的轴颈插在轴承之中,因此,小曲拐两端轴颈的应力应变很小。从图中可以看出小曲拐的发生最大应力、应变的位置在小曲拐退刀槽附近,两端的轴颈应力应变很小,符合之前小曲拐刚性区域的建立。

图10 小曲拐1应力与应变等值云图
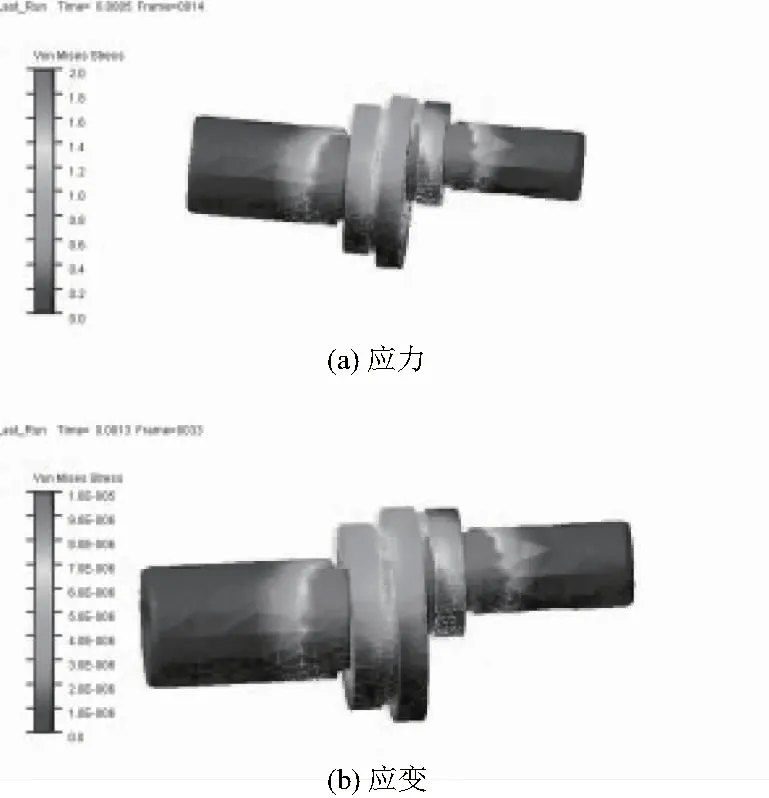
图11 小曲拐2应力与应变等值云图
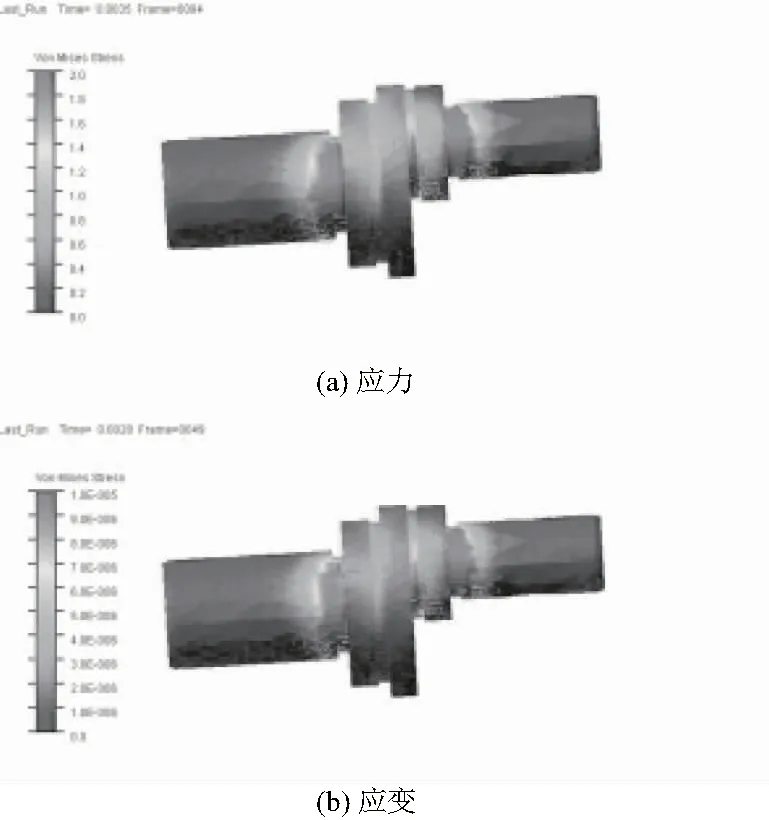
图12 小曲拐3应力与应变等值云图
图13-图15所示的是小曲拐应力、应变最大的节点1 703(从图7-图9可以看出3个小曲拐的发生最大应力、应变的节点编号均为1 703)的应力、应变随主轴转动一周的变化情况。由图中可以看出,3个小曲拐应力应变的变化规律基本一致,进一步说明了涡旋压缩机3个小曲拐受力情况与运动规律基本相同,符合小曲拐平面四杆机构的运动规律。由于涡旋压缩机电动机刚开始驱动,因此图中刚开始会出现一个突变状况,由图中看出3个小曲拐的最大应力约为11N/mm2,而最大应变约为7×10-5mm。由此可见,小曲拐的变形还很小的,因此选择的小曲拐符合涡旋压缩机防自转的要求,并为小曲拐的进一步优化设计提供重要的参考。
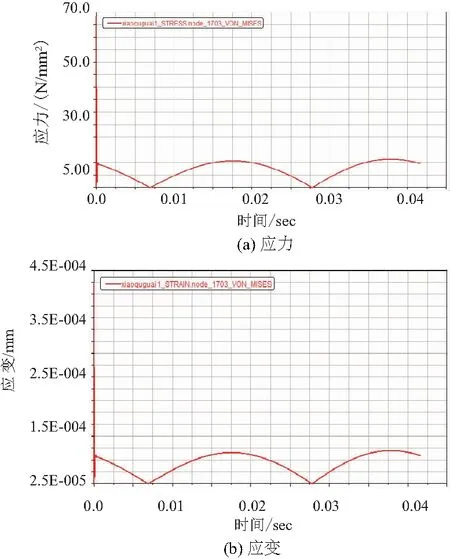
图13 小曲拐1最大应力点应力与应变
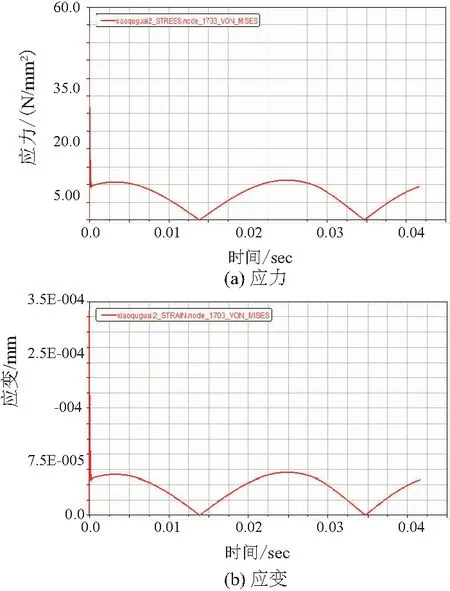
图14 小曲拐2最大应力点应力与应变


图15 小曲拐3最大应力点应力与应变
5 结语
1) 利用Ansys与Adams联合仿真,建立了涡旋压缩机的刚柔耦合模型。
2) 通过小曲拐应力最大的10个节点可以看出:3个小曲拐应力最大的前7个节点是相同的。
3) 通过应力应变等值云图中可以看出小曲拐最大变形位置在退刀槽附近。
4) 通过小曲拐最大节点应力应变的变化趋势得知3个小曲拐有相似的运动规律与受力状况。符合小曲拐平面四杆机构的运动规律,为小曲拐进一步的优化提供重要的参考。

