γ型斯特林热机无益容积比的影响分析

曲家闯，许国太，张学林，张 安

（兰州空间技术物理研究所 真空技术与物理重点实验室，兰州 730000）

0 引言

热气机主要可以分为三类：开式循环热气机、外部燃烧开式循环热气机和外部燃烧闭式热气机[1]，而斯特林热机则属于外部燃烧闭式热气机，根据基本构型不同可以分α型（双活塞式）、β型（配气活塞式）、γ型（双缸配气活塞式），其理论循环效率可以达到同等温度下的卡诺循环效率，在影响循环效率、输出功率的参数选取时，要选择恰当的运行参数，使各参数间有良好的匹配性[2]，而无益容积比则是设计中最难选择的一个参数[3]。无益容积指的是活塞未扫到的容积，包括气缸余隙、加热器、冷却器、回热器的流通容积及其连接管道、孔口的内部容积[4]；无益容积比则为无益容积与膨胀腔活塞扫气容积的比值。无益容积比过大时，表明各换热器中的换热面积较大，换热效果较好，但由于无益容积过大，系统的压比急剧降低，造成输出功率和效率都下降；无益容积过小时，由于换热不充分，造成热端与冷端温差降低，不利于提高输出功率与效率。因此，通过建立等温模型及换热器（加热器、冷却器）模型对γ型斯特林热机进行无益容积比影响分析。

1 γ型斯特林热气机基本结构

γ型斯特林热气机又叫双缸配气活塞式热气机，基本结构如图1所示，两个活塞分别安装在两个气缸中，靠近加热器一侧的活塞为配气活塞，另一个活塞称为动力活塞。配气活塞与气缸组成的腔室叫膨胀腔（热腔），配气活塞与动力活塞所组成的腔室叫压缩腔（冷腔），动力活塞与缸体形成的腔室叫背压腔，而加热器、回热器、冷却器串联一起处在配气活塞外侧与气缸内侧的环形区域中。

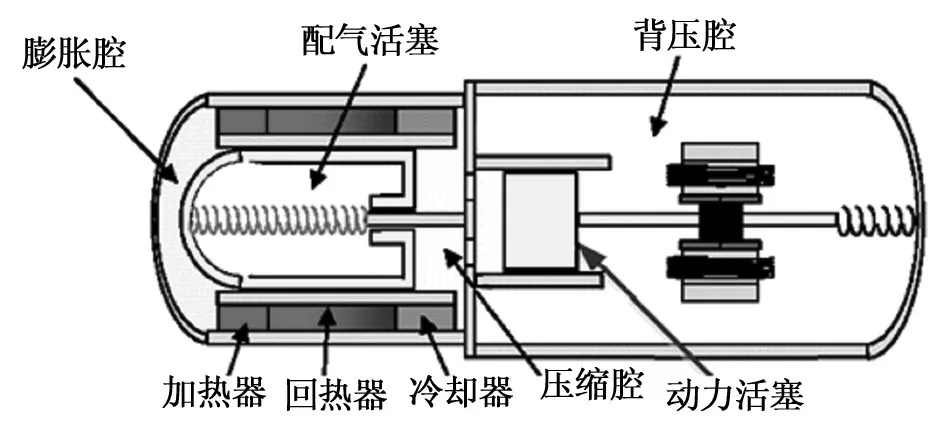
2 γ型斯特林热气机的模型建立

2.1 等温模型建立

采用等温分析模型，在建模过程中，假定以下条件：

（1）压缩腔和膨胀腔中进行的是等温过程，即等温压缩过程和等温膨胀过程；

（2）压缩腔和膨胀腔的容积按正弦规律变化；

（3）工质符合理想气体方程，即pV=MRT；

（4）回热过程是理想的，不存在不可逆损失；

（5）整个系统的瞬时压力相同，即工质流经加热器、回热器、冷却器等无压力损失；

（6）各工作腔内的温度均匀一致。

根据以上假设，得出瞬时热腔容积：

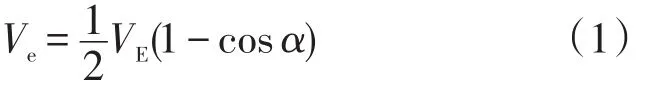
瞬时冷腔容积：

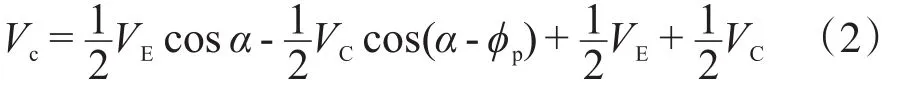
总无益容积：

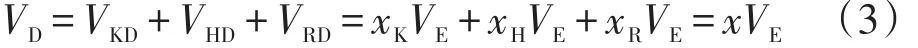
其中，冷却器无益容积：VKD=xKVE；加热器无益容积：VHD=xHVE；回热器无益容积：VRD=xRVE。

总容积VS为：

式中：Ve为瞬时热腔容积；α=ωt，ω为运行的角速度；t为图1中配气活塞从最左侧开始算起的时间；VE为配气活塞最大行程容积；Vc为瞬时冷腔容积；VC为动力活塞最大行程容积；φp为配气活塞领先与动力活塞运行的活塞领先角（活塞相位角）；VD为总无益容积；x为无益容积比；xK为冷却器无益容积比；xH为加热器无益容积比；xR为回热器无益容积比。

因为循环过程中工质总物质的量M保持不变，且认为内部各处压力相等可有：

式中：me为热腔工质物质的量；mc为冷腔工质物质的量；mk为冷却器工质物质的量；mr为回热器工质物质的量；mh为加热器工质物质的量；TE为膨胀腔工质温度；TH为加热器中工质温度，一般TE=THΔTHE，ΔTHE在60～100 ℃之间[2]，取ΔTHE为80 ℃；TC为压缩腔工质温度；TK为冷却器中工质温度，TC=TK+ΔTKC，ΔTKC在20～50 ℃[2]，取ΔTKC为20 ℃；TR回热器平均温度

其中：

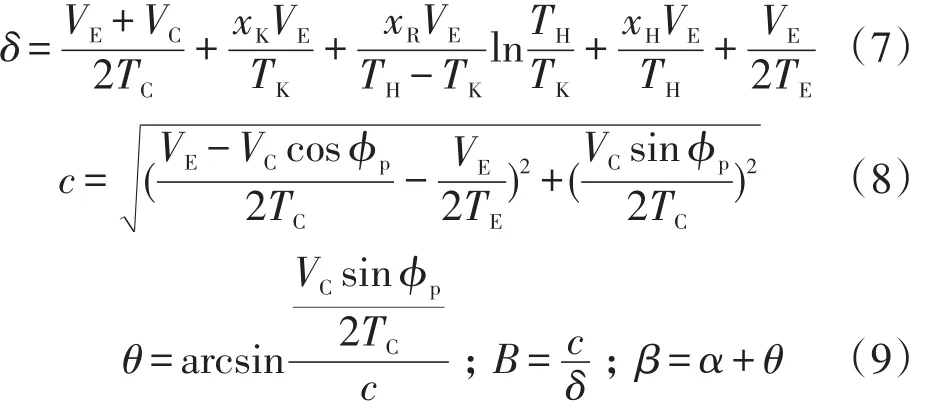
可求得瞬时压力p为：

等温压缩功WC等于冷却器带走的热量Q2，则：

其中φp为活塞相位角。

循环功为：

等温膨胀功WE等于外源供给系统的热量Q1，则：

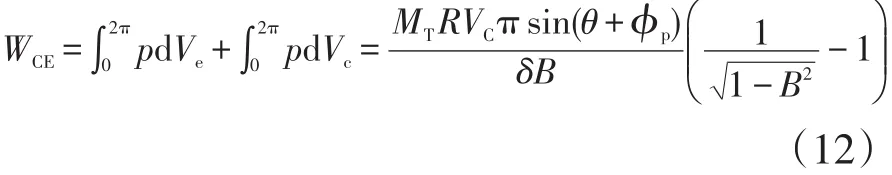
则系统输出功率为：

式中：f为运行频率。

2.2 加热器、冷却器换热模型建立

加热器、冷却器是斯特林热机的关键部件，是影响发动机性能最主要的部件。通常斯特林热机中的工质处于加压状态，密度较大，流速较高，工质大多采用氢气和氦气。加热器一般选用导热性能良好的金属材料，因此加热器与内部工质的换热能力是足够的，对加热器而言，受制约的传热过程一般是外部热源对加热器的传热，故加热器一般为外部翅片式，结构如图2所示。冷却器中冷却工质一般为低温水，换热系数远大于内部工质与冷却器的换热系数，故冷却器一般采用内部翅片式结构，结构如图3所示。

图2 加热器结构示意图Fig.2 Schematic diagram of heater

图3 冷却器结构示意图Fig.3 Schematic diagram of cooler

对加热器与冷却器建模作如下假设：

（1）加热器、冷却器分别为热源与冷源，计算时只考虑内壁或内翅片的对流换热；

（2）假设加热器及冷却器表面温度恒定且各处温度均匀一致。

则加热器、冷却器表面温度及内部工质温度关系可由牛顿冷却公式给出：

此处对流传热关联式采用经典的管内强制对流换热式Dittus-Boelter公式[5]：

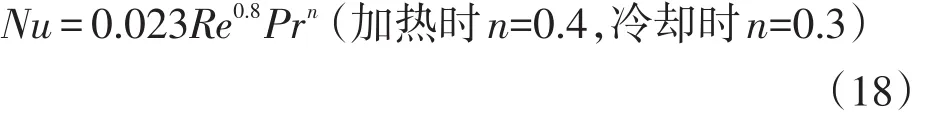
式中：Q1为加热器向内部工质输入的热量；Q2为冷却器从内部工质带走的的热量；Tw1为加热器壁面温度；Tw2为冷却器壁面温度；h1为加热器壁面与内部工质的对流换热系数；h2为冷却器壁面与内部工质的对流换热系数；Nu为努赛尔数；Re为雷诺数；Pr为普朗特数。

3 仿真计算及结果分析

在MATLAB中根据建立的计算模型编制m文件，对加热器和冷却器进行仿真计算时需要使用氦气的物性参数，通过直接在MATLAB中调用Refprop软件提供的m文件实现氦气物性参数的计算。计算时先通过等温模型算出系统输出功率Wnet、等温膨胀功WE以及等温压缩功WC，再通过加热器、冷却器模型计算出此时加热器、冷却器的本体温度，计算初始参数如表1所列。

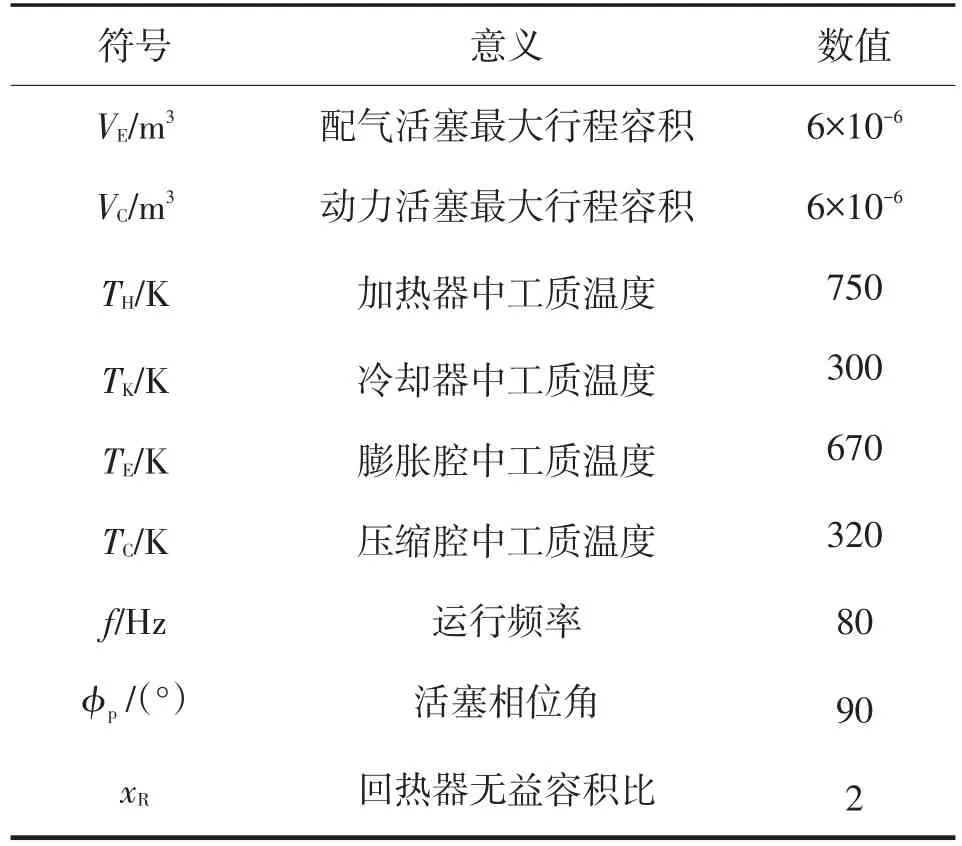
表1 计算初始参数Table1 Parameter table

3.1 加热器无益容积对系统影响

在保持冷却器无益容积比、回热器无益容积比、加热器、冷却器中工质温度不变的情况下，改变加热器无益容积比，观察加热器本体温度与内部工质温差ΔTH、系统输出功率随加热器无益容积比的变化如图4所示。可以看出，在随着加热器无益容积比的增大，加热器本体温度与内部工质温差ΔTH逐渐减小，且减小趋势越来越弱，由于加热器无益容积比的增大，内部工质与加热器的换热面积越大，换热能力越强，所需维持内部工质温度的加热器温度就越低，在加热器无益容积比分别为0.37、1.48时，二者温差分别为342 K、82 K，可见增大加热器无益容积比，对提高换热能力成效显著；系统的输出功率则随着加热器无益容积比增大而减小，且减小幅度越来越明显，这是由于加热器无益容积比增大，系统死容积增大，压缩比较小，导致输出功率减小。

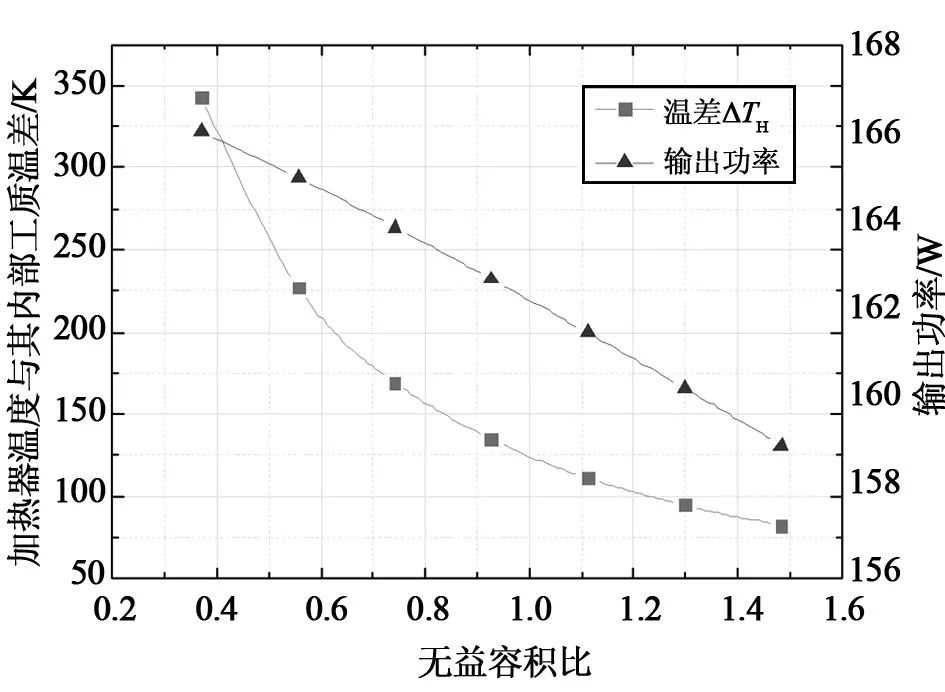
图4 系统参数随加热器无益容积比变化曲线Fig.4 Variation of system parameter with unhelpful volume radio of heater

3.2 冷却器无益容积对系统影响

在保持加热器无益容积比、回热器无益容积比、加热器、冷却器中工质温度不变的情况下，改变冷却器无益容积比，观察冷却器内部工质温度与冷却器之间温差ΔTK、系统输出功率随冷却器无益容积比的变化如图5所示。可以看出，随着冷却器无益容积比的增大，冷却器内部工质温度与冷却器之间温差ΔTK逐渐减小且减小趋势越来越弱，由于冷却器无益容积比的增大，内部工质与冷却器的换热面积越大，换热能力越强，在同等换热量下所需温差就小；系统的输出功率则随着冷却器无益容积比增大而减小，与加热器无益容积比增大导致输出功较小的原因一致，都是由于冷却器无益容积比增大，系统死容积增大，压缩比较小，导致输出功较小，但随着冷却器无益容积比增大，系统输出功减小幅度则与加热器不同，减小的幅度越来越小。

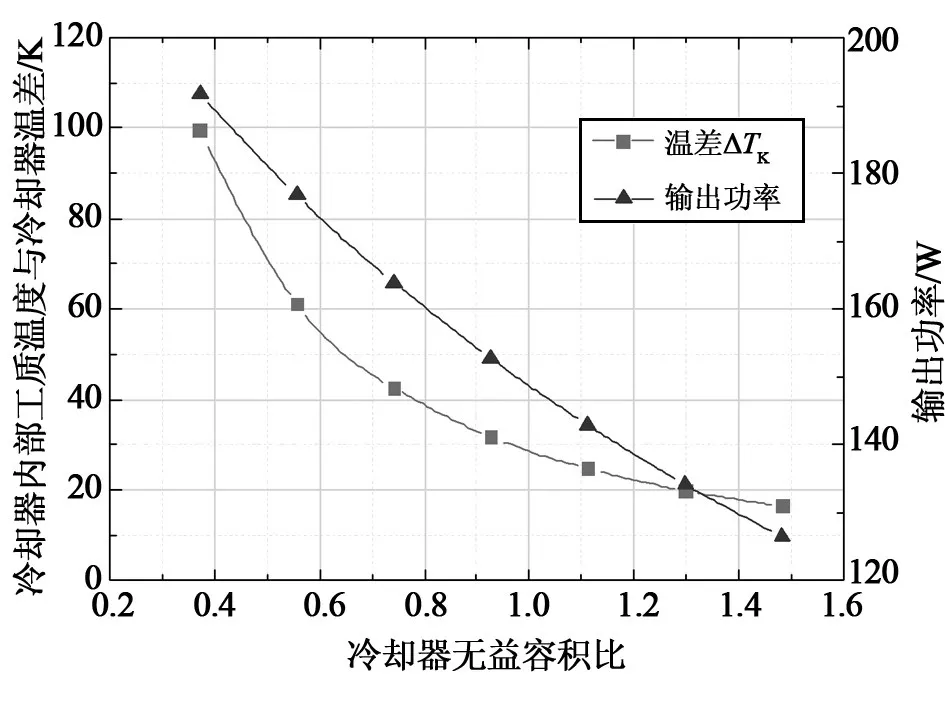
图5 系统参数随冷却器无益容积比变化曲线Fig.5 Variation of system parameter with unhelpful volume radio of cooler

3.3 总无益容积比不变时加热器无益容积比对系统的影响

相对卡诺循环效率是工作温度相同的实际循环的效率与可逆卡诺循环效率的比值，反应了实际循环效率接近卡诺循环的程度，相对卡诺循环效率越大则技术经济性越好。保持加热器与冷却器总的无益容积比不变，改变加热器无益容积比，观察相对卡诺循环效率随加热器无益容积比的变化如图6所示。

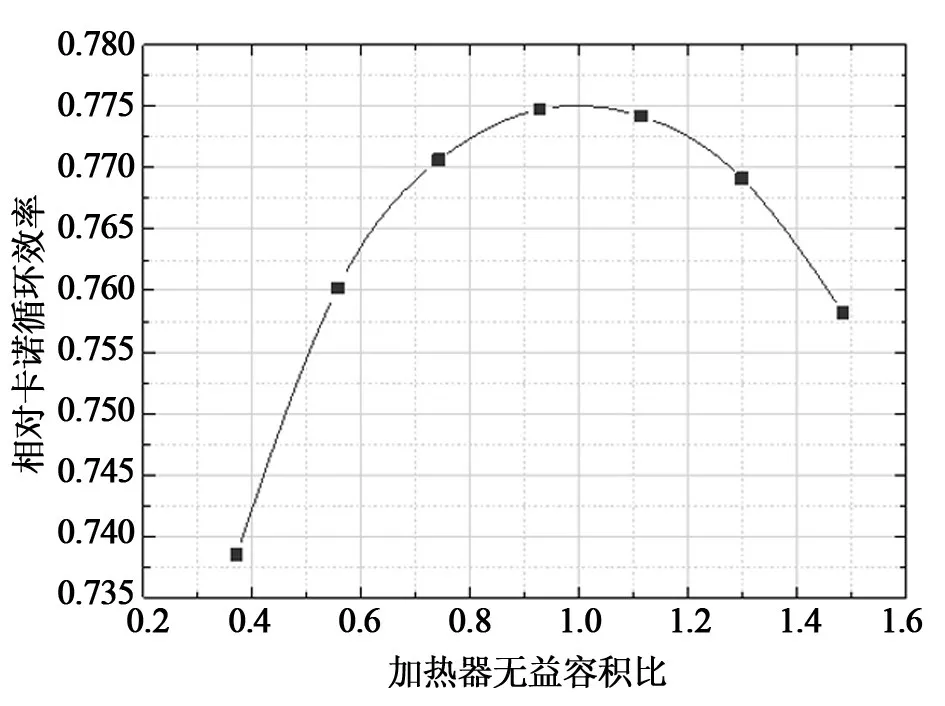
图6 相对卡诺循环效率随加热器无益容积比变化曲线Fig.6 Variation of relative Carnot cycle efficiency with unhelpful volume radio of heater

在加热器、冷却器总无益容积不变时，系统的相对卡诺循环效率随着加热器无益容积比的增大先增大再减小，在本模型中加热器无益容积比为1左右时相对卡诺循环效率取得最大值，这说明在加热器、冷却器总体积不变的情况，存在一个最佳点使得系统的相对卡诺循环效率最大。

3.4 加热器与冷却器无益容积比对输出功率的影响对比

将3.1、3.2节中，分别保持冷却器、加热器无益容积比不变，输出功率随加热器、冷却器无益容积比变化的数据进行对比，观察二者对系统输出功率的影响大小，如图7所示。可以看出，加热器无益容积比从0.4增加到1.4时，系统输出功率减少了约6 W，而冷却器无益容积比从0.4增加到1.4时，系统输出功减少了约为60 W左右，说明加热器无益容积比对系统的输出功率影响相对于冷却器无益容积比的影响小很多，因此设法减小冷却器的无益容积比对提高系统输出功率有着显著的效果。

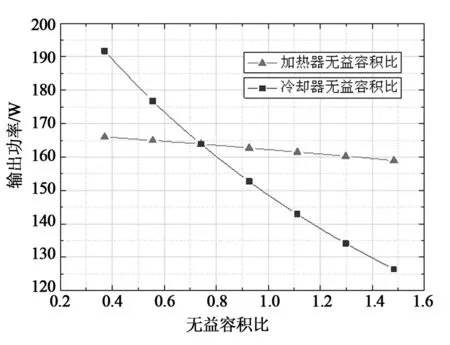
图7 加热器、冷却器无益容积比对系统输出功率的影响曲线Fig.7 Variation of system output power with unhelpful volume radio

4 结论

通过建立γ型斯特林热机的等温模型，对系统循环进行了仿真，并建立了加热器、冷却器换热计算模型，对加热器无益容积比、冷却器无益容积比对系统的输出功率、相对卡诺循环效率、加热器及冷却器本体温度的影响进行了分析，得出结论：

（1）在冷却器无益容积比不变时，随着加热器无益容积比逐渐变大，系统输出功率减小且减小趋势越来越大，加热器本体温度与内部工质温差ΔTH逐渐减小；

（2）在加热器无益容积比不变时，随着冷却器无益容积比逐渐变大，系统输出功率减小且减小趋势越来越小，冷却器内部工质温度与冷却器之间温差ΔTK逐渐减小；

（3）在加热器、冷却器总无益容积不变时，加热器无益容积比、冷却器无益容积比存在一个最佳点使得系统的相对卡诺循环效率最高；

（4）对比加热器无益容积比、冷却器无益容积比对系统输出功率的影响，冷却器无益容积比影响更大，说明设法减小冷却器无益容积比可以显著的提高系统输出功率。