铯原子钟优化算法中微波幅度控制方法的研究

马 沛，陈 江，董鹏玲，王 骥，崔敬忠

（兰州空间技术物理研究所 真空技术与物理重点实验室，兰州 730000）

0 引言

原子钟是高精度时间频率系统的核心。铯原子钟具有频率准确度高、稳定度好、漂移率低的特点，成为国际一级时间频率标准。分布在全球的数百台商品铯钟配合部分氢钟和极少量高精度基准钟共同构成了国际原子时守时系统。作为守时钟使用时，铯钟一般放置于温度、湿度严格受控的专用屏蔽实验室内，工作环境相对简单。

近年时频体系建设发展迅速，除了传统的地面守时、授时应用领域，在天基守时、导航卫星、军用时统、民用通信等领域越来越多的需要应用商品铯钟[1]。应用领域的扩展要求铯钟能够在温湿度变化较大，电磁环境较差的环境中长期稳定运行。国产磁选态铯钟原型机工作在精确控温控湿的专用守时实验室环境中，长期稳定度指标10万秒处为6.0E-14，普通无控温实验室环境测试时，长期稳定度指标在10万秒处为1.3E-13，复杂环境下，稳定度指标显著恶化。

针对国产铯钟对环境变化敏感的问题，分析了磁选态铯原子钟中影响频率准确度和长期稳定度的因素。通过研究微波幅度对整钟频率影响及其与原子跃迁几率关系，由于铯束管内存在Rabi牵引、Ramsey牵引、微波腔牵引，钟的输出频率对微波幅度敏感[4-5]，是影响整机长期稳定度指标的一个重要原因。为了有效的抑制某些动态影响因素和硬件电路本身存在的参数衰减造成的微波幅值变化，提出一种采用软件算法结合硬件电路对微波幅度进行实时控制的方法，与使用固定微波幅度参数的办法相比，提高了整钟长期稳定度指标，取得了较好的结果。

1 环境温度变化对频率影响的机理分析

磁选态铯钟在测试中发现其频率稳定度对环境温度变化较为敏感，影响了整机在温度变化环境中的长期稳定度指标。经过分析，由于整机微波链路放大器件存在温度系数，造成微波幅度存在波动，另外温度变化引起微波谐振腔形变，造成腔体失谐。由于存在Rabi牵引、Ramsey牵引和腔体失谐效应，微波幅值和谐振腔形变两个因素会造成整机输出频率漂移[9]，下面逐一进行分析。

1.1 Rabi牵引效应造成的整机频率漂移

Rabi牵引的大小与微波幅度和原子速率分布紧密相关，在微波谐振腔调谐良好的情况下，Rabi牵引是将微波幅度变化转化为钟频率变化的主要耦合因素[4，8]。Rabi牵引造成的相对频率偏移跟原子飞行速度、原子跃迁线幅度、跃迁线频率差相关，正比于1/L2l2，l为振荡场区长度，L为两个振荡场之间的间隔[9]。原子飞行速度，原子跃迁线幅度和跃迁线频率差与环境温度不相关，仅考察温度对谐振腔的影响。

微波腔由无氧铜制作，振荡区长度l的典型值为1 cm，L的典型值为17 cm。一般铯束管内部Rabi牵引造成的频率偏移在10-15量级。无氧铜线膨胀系数18.6×10-8℃-1，温度波动50℃时，相对频率偏差变化为3.74×10-5，对整机频率偏差的影响在10-20量级，对整机频率稳定度指标的影响可忽略不计。

1.2 Ramsey牵引效应造成的整机频率漂移

当激励跃迁的微波辐射场存在垂直于C场的分量时，在中心跃迁频率附近就会产生σ跃迁，虽然相对于π跃迁的幅度，σ跃迁的幅度很小（图1中中心跃迁谱线两侧凹坑内的干扰波形），难以观测到，但与中心跃迁的距离更近，只有相邻π跃迁的一半，因而对中心跃迁频率的牵引（即Ramsey牵引）仍然存在。Ramsey牵引引起的频率偏移正比于l/L，正比于H2，H为微波辐射场强度[9]

因此，Ramsey牵引引起的频率偏移与微波辐射场幅度以及腔体尺寸有关。由于频率偏移正比于l/L微波谐振腔线膨胀抵消。一般铯束管内部Ramsey牵引造成的频率偏移在10-16量级。由于Ramsey牵引效应的存在，当温度波动引起微波场幅度波动，会造成整机频率偏移量的波动，影响整机稳定度指标。

1.3 腔体牵引效应造成的整机频率偏移

当微波腔未准确调谐到原子中心跃迁频率上时，会对中心跃迁频率产生牵引，其相对值为[7]：

式中：υ0为原子跃迁中心频率；ΔυC为微波腔失谐频率；为频率的相对变化；T为微波腔响应时C间；Ti为原子在两个振荡场间飞行的时间特征参数。

一般来说，的值与的值大致相当，Q为C微波腔的有载Q值，Ql为Ramsey线形的Q值。当采用慢方波频率调制时，ΔC与微波幅度和频率调制深度相关。当微波腔失谐0.1 MHz时，腔体频率牵引可能达到10-13量级，如果微波功率变化1 dB，则频率牵引可能达到2.3×10-13[3，7]。

另外，当外界环境温度变化时，原本已经调谐到原子跃迁中心频率的微波腔有可能由于腔体膨胀或缩小而失谐，影响施加给原子的有效幅度，频率的相对偏移与温度变化的关系为[7]：

式中：α为微波腔材料的线性膨胀系数；ΔT为温度变化。温度变化1 K，α=1.6×10-5K-1时，频率牵引同样可能达到10-13量级[7]。

2 改善整机温度系数的方法

要满足铯钟使用范围扩展的实际需求，必须解决整机温度系数问题，由于温度变化环境客观存在，微波谐振腔的形变无法避免，因此必须控制微波幅值进行补偿。

研究微波幅度与跃迁几率的关系，在分离振荡场铯束管内，原子的跃迁几率取决于微波场幅度和原子速率分布函数。原子从m态跃迁到n态的几率为[9]

式中：Δω=ω0-ω，ω0为原子平均跃迁频率，ω为微波辐射场频率；τ=l/v为原子与单个振荡场（微波场）的作用时间，v为原子飞行速度。T=L/v为原子在C场中的飞行时间。cosθ=（ω0-ω）/a，sinθ=-2b/a，a=[（ω0-ω）2+（2b）2]1/2，2b正比于微波场强度。

对于不同速率的原子，跃迁几率：

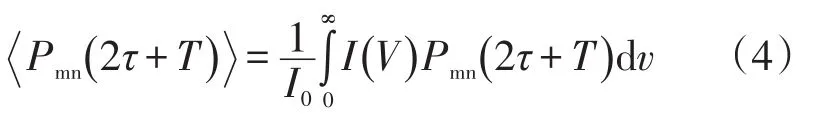
速率在v至dv内的束强为：

式中：I0为总束强；α为容器内原子的最大几率速率。当微波辐射场幅度H1相对于最佳微波辐射场幅度H0变化时[10]，相对微波辐射场幅度（单位dB）：

根据式（3）～（6）对微波幅度与原子跃迁几率进行仿真结果如图1所示，可以看到，存在一个使跃迁几率最大的微波幅度最佳值H0；当微波幅度偏离最佳值时，无论幅度增加还是减小都会降低跃迁几率。在微波幅度最佳值（H1=H0）附近，跃迁几率相对于微波幅度的变化率达到最小值。

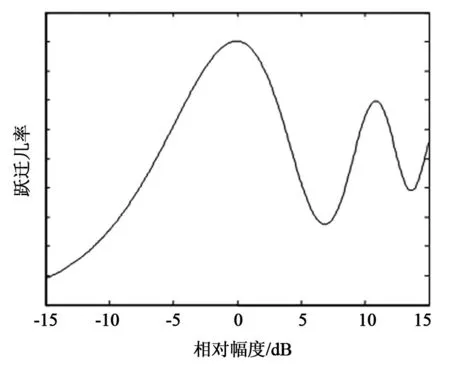
图1 微波幅度与跃迁几率的关系仿真结果曲线Fig.1 Simulation of transition probability vs.microwave amplitude

3 微波幅度的控制方法

Rabi牵引、Ramsey牵引、微波腔牵引等因素会造成频率偏移对微波幅度敏感，虽然可以通过更加精细的束光学、偏转磁场和C场线圈的设计与加工使Rabi牵引和Ramsey牵引得到改善[2]，通过谨慎选择C场值减小频率对微波幅度的敏感程度[4]，但是试验表明这些措施难以得到理想的结果，上述因素对长期频率稳定度的影响难以彻底消除；温度的变化仍然会产生微波腔失谐，降低作用于原子的微波磁场幅度，温度变化对电子线路的影响会使微波幅度难以稳定。因此，为了达到频率准确度和稳定度的高指标要求，采用软件算法结合硬件电路对微波幅度进行控制，并取得了较好效果。

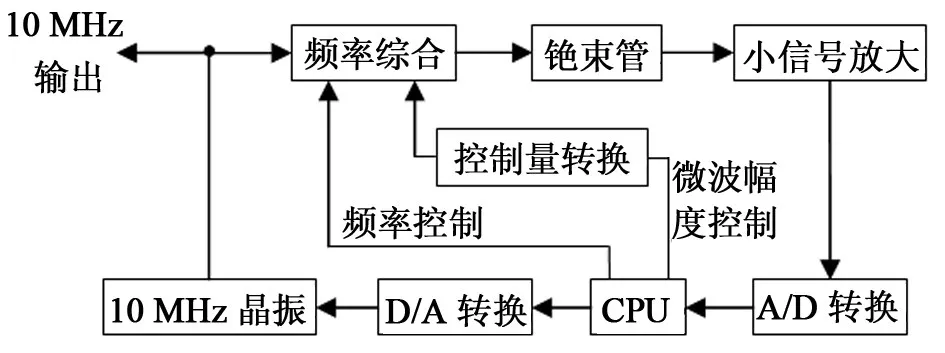
频率综合电路以10 MHz信号作为参考信号合成中心频率位于9.19×104MHz附近的微波信号，用来激励铯束管内的原子跃迁；跃迁后的原子经过一系列的物理过程后转化为电流小信号从铯束管输出；小信号经放大、A/D转换后进行采样；当频率综合电路采用慢方波调频的方式对微波信号进行调制时，CPU可根据不同频率调制点上的采样值计算出微波频率的偏离量[2]，然后根据频率偏离量来调节10 MHz压控晶振的输出频率。铯束管输出小信号的幅度在其他参数恒定时正比于原子跃迁几率，因此，可以根据微波幅度与跃迁几率的关系对微波幅度进行控制，控制方法原理如图2所示。

微波幅度与跃迁几率的关系如图1所示，当微波幅度达到某个值时，原子跃迁的几率达到最大值。在最大值处，曲线的斜率为零，即d（Pmn）/d∏=0，微波幅度的微小波动对跃迁几率的影响达到最小，此时Rabi牵引、Ramsey牵引和腔体失谐等因素对频率的影响最小。跃迁几率的最大值处即为软件控制算法对微波幅度进行控制的目标位置。

铯钟伺服系统中，CPU输出的数字信号经D/A转换和V/I转换后变为控制电流输送给混频器的IF端，LO端接9.2 GHz微波信号，RF端输出经过幅度控制的微波信号。采用单平衡二极管混频器作为幅度调制器，未采用常用的PIN管，原因是PIN管热瞬变可能导致相位瞬变，从而引起频率误差[11]；单平衡二极管混频器可以较好地避免这一问题。微波幅度控制部分的原理如图3所示。

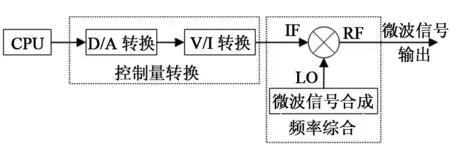
4 试验验证

采用上述方法对微波幅度进行控制后，频率稳定度测试结果如图4所示，通过与不进行幅度控制的测试结果（其他测试条件相同）对比表明：两个测试在短稳部分的曲线基本重叠，从4 000 s开始，两条曲线走势发生分化，有幅度控制的测试曲线基本按相同的斜率变化，而无幅度控制的测试曲线逐渐趋平。有幅度控制时的频率准确度为8.58×10-13，高于无幅度控制的7.08×10-12。

图4 频率稳定度测试结果对比图Fig.4 Results of Frequency stability contrast test

5 结论

从微波幅度对钟频率影响的机理入手，分析得到了铯束管内Rabi牵引、Ramsey牵引和腔体牵引等因素的影响导致频率偏移值对微波幅度敏感的结论；从机理分析中还得知，Rabi牵引和腔体牵引对频率偏移的影响较大，Ramsey牵引的影响相对较小。在铯原子钟系统中，由于铯束管输出小信号的幅度是控制回路唯一的判据，并且在电子倍增器增益不变（控制环路足够快，在控制周期内可以认为倍增器增益恒定）时小信号幅度正比于原子跃迁几率，因此有必要对微波幅度与跃迁几率之间的关系进行分析。对微波幅度与跃迁几率的理论仿真分析表明，每支铯束管都存在一个微波幅度最佳值，在该值附近微波幅度的变化对（4，0）↔（3，0）跃迁的影响最小。基于上述分析，提出一种软件算法结合硬件电路将微波幅度控制到跃迁几率曲线的最大值附近的控制方法。对比试验结果表明这种方法能够明显地减小微波幅度对频率偏移的影响，从而有效地改善铯原子钟的频率准确度和长期稳定度。