基于非线性模式分解的旋转机械复合故障特征提取方法
杨 宇 李 鑫 潘海洋 程军圣
湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082
0 引言
对旋转机械进行故障诊断对保障机械设备的安全和稳定运行具有十分重要的意义。大量工程实践表明,机械设备中的故障往往不是单一故障,而是复合故障。当发生复合故障时,多种故障特征之间会相互干扰、相互耦合[1];此外,在强大背景噪声下,旋转机械的微弱故障特征很容易被噪声淹没,这都给复合故障的诊断带来了巨大的挑战。传统的时域或频域分析方法只适用于线性平稳信号,而复合故障的振动信号多为非线性、非平稳信号,仅仅使用时域或频域分析方法往往不能有效提取出故障特征[2]。时频分析方法由于实现了信号时频域的联合显示,在旋转机械故障诊断中的应用越来越广泛。
加窗傅里叶变换(windowed fourier transform,WFT)和小波变换(wavelet transform,WT)是信号处理中常用的时频分析方法,在时间域和频率域上都具有表征信号局部特征的能力,特别适用于非线性、非平稳信号的处理[3-4]。根据Heisenberg测不准原理,对于任何一种时频变换,频率分辨率和时间分辨率不能同时达到最优。WT的频率分辨率随着频率的增加而降低,而其时间分辨率提高,由此可以用WFT来获得高时间分辨率;而WFT频率分辨率不变,由此可以用WFT获得高频率分辨率。
经验模态分解(empirical mode decomposition, EMD)是HUANG等[5]提出的一种自适应的非线性信号处理方法,具有较强的信噪比,已被广泛应用于旋转机械的故障诊断中[6-7]。在EMD的基础上,WU等[8]又提出了对信号加入白噪声的集合经验模态分解(ensemble empirical mode decomposition,EEMD)方法。EMD和EEMD的基本思想都是根据信号本身的尺度特征,将信号分解成多个固有模态函数(intrinsic mode function,IMF)分量,但这两种方法分解产生的分量并不总是具有物理意义,易形成伪分量;同一激励源产生的非正弦复杂分量将分解成多个简单分量,使分量数量增加。此外,它们对噪声都很敏感,噪声鲁棒性不理想。
上述缺点极大限制了EMD和EEMD在实际中的应用,鉴于此,IATSENKO等[9]提出了一种新的时频分析方法——非线性模式分解(nonlinear mode decomposition,NMD)方法。该方法将非线性、非平稳信号分解为一系列非线性模态(nonlinear mode,NM)分量。在分解过程中融合了WFT和WT的优势,提高了信号分解和重构精度;利用谐波辨识既减少了所得分量的个数,又保证了每个分量都具有实际物理意义;采用基于傅里叶变换的替代数据方法进行噪声检测,提高了噪声鲁棒性。
本文通过仿真信号分析,结果表明NMD相比于EEMD具有显著的优越性。然后将该方法应用于旋转机械复合故障诊断中,对齿轮—轴承复合故障振动信号进行NMD分解,得到若干个NM分量,再对分量进行包络谱分析,根据提取的故障特征进行诊断。
1 NMD分解原理
在非线性系统的某一激励下,把系统的响应称为一个NM分量。设信号由一系列NM分量和噪声组成:
(1)
其中,η(t)为噪声,ci(t)为NM分量,每个ci(t)可表示成一系列调幅调频谐波叠加:
(2)
rh=Ahcosφh
(3)
其中,v(φ(t))为周期为2π的周期函数,rh(t)表示ci(t)的第h个谐波,r1(t)为此分量的主谐波,rh(t)(h=2,3,…)为次谐波。

(1)对原始信号进行小波变换。给定信号s(t),其WT可表示为
(4)

(5)
其中,Gs(w,t)为式(4)所代表的公式;wp(tn)为t=tn时脊线wp的表达形式;tn表示第n个峰值;〈f(t)〉和std[f(t)]分别为f(t)的平均值和标准偏差。

(6)

(4)选择最优的时频变换。为了提高分解精度,融合WT和WFT两种时频变换的优点,使NMD分解根据经验公式自适应地选择时频变换类型,经验公式可表示为
K=(1+V[∂tv(t),v(t)])-1+
(1+V[∂tA(t),v(t)])-1
(7)
若K>1,则继续选用WT;反之,则选用WFT。
(5)确定重构方法。为了使重构的谐波更加准确,结合脊线法和直接法两种重构方法的优点[10],确定谐波重构的最终方法。
①如果WFT为最优时频变换,则需要对原始信号s(t)进行WFT:

(8)
其中,g(t)表示高斯窗函数。再根据式(4)提取脊线,对于WFT,脊线的提取只需要将式中对数频率尺度lnwp改为wp,然后用直接法和脊线法分别重构参数A(d,r)(t)、φ(d,r)(t)、v(d,r)(t)(r表示脊线法,d表示直接法):
(9)
(10)
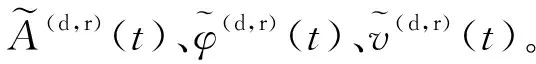
对于各谐波参数,选择不一致系数大的重构方法,谐波参数的不一致系数可表示为
(11)

②如果根据式(11),WT是最优的,则再用直接法重构谐波参数:
(12)
同理,利用式(11)选择最优参数重构参数。
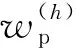
(7)谐波的辨识。提取次谐波rh(t)后,通过时移替代数据检验主谐波r1(t)和次谐波rh(t)零假设的独立性来辨别谐波真伪[11]。对于主谐波r1(t),其替代参数可表示为
(13)
其中,N为采样长度;fs为采样频率;d为替代数据的时移点数;M为替代数据的最大时移。
对于次谐波rh(t),替代参数的产生过程如下:
①将时频信号在时域上前移ΔTd/2,即G(w,τ+ΔTd/2)或W(w,τ+ΔTd/2)。
(14)
(15)
(16)
总体一致性系数可表示为
(17)

⑤为了避免谐波之间的干扰造成误判,谐波辨识时要将前一个真谐波从原始信号中减去(在对次谐波r2(t)辨识时,也要将主谐波r1(t)从原始信号中减去)。
(8)噪声检验。将提取出的所有真谐波相加得到一个NM分量ci(t),然后将ci(t)从原始信号中移除,并对剩余信号重复执行上述过程,直到剩余信号只含有噪声。使用基于傅里叶变换的替代数据[12]方法检验剩余信号是否只含噪声,替代数据的统计特征D取为
(18)

(1)提取出ci(t)的主谐波r1(t),并计算其统计特征D0(αA,αv)。
(2)产生Ns个傅里叶变换替代数据,计算各自的统计特征Ds=1,2,…,Ns(αA,αv)。

NMD流程见图1。

图1 NMD流程图 Fig.1 Flow chart of NMD method
2 仿真信号分析
为了说明NMD时频分析的性能,将其与EMD或EEMD进行对比。相比EMD,EEMD通过在原始信号中添加白噪声并对其进行EMD分解,在一定程度上解决了EMD频率混叠问题,增强了噪声鲁棒性。鉴于EEMD的优势,同时为了节省篇幅,本文只与EEMD进行对比。
为不失一般性,本文选择一个调幅调频信号、一个正弦信号和一个高斯白噪声信号之和进行仿真分析,仿真信号和各分量如下:
(19)
其中,η(t)为N[0,1]均布高斯白噪声,采样频率为1 024 Hz,采样时间为1 s。仿真信号及各分量的时域波形见图2。

图2 仿真信号及两个分量时域波形Fig.2 Time domain waveform of simulation signal and two components
对仿真信号分别进行EEMD和NMD分解,EEMD分解时加入高斯白噪声振幅系数K=0.25,总体平均次数为100。NMD分解过程中各参数自适应选择结果见表1,噪声检测预设置信水平ls=95%,谐波辨识时预设置信水平l=95%。EEMD和NMD的分解结果见图3和图4。

表1 NMD中参数自适应选择
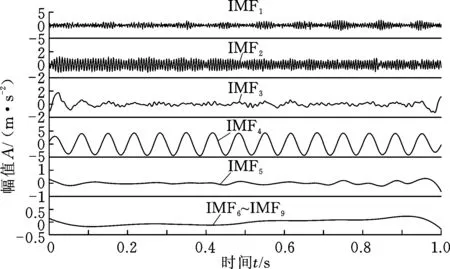
图3 EEMD信号分解结果Fig.3 EEMD decomposition results

图4 NMD信号分解结果Fig.4 NMD decomposition results
从分解结果可以看出:EEMD分解出9个IMF分量,仿真信号中复杂分量x2(t)被分解成多个简单分量,使IMF分量变多,其中一些IMF分量根本没有物理意义,如IMF5~IMF9。同时由于受到噪声的影响,有些IMF分量中存在一定程度的模态混叠现象,如IMF1、IMF2;而NMD只分解出了2个NM分量,没有提取出多余的分量,NM1分量对应仿真信号分量x1(t),NM2分量对应分量x2(t),且各NM分量与各仿真信号分量基本一致,各分量的误差曲线见图5。
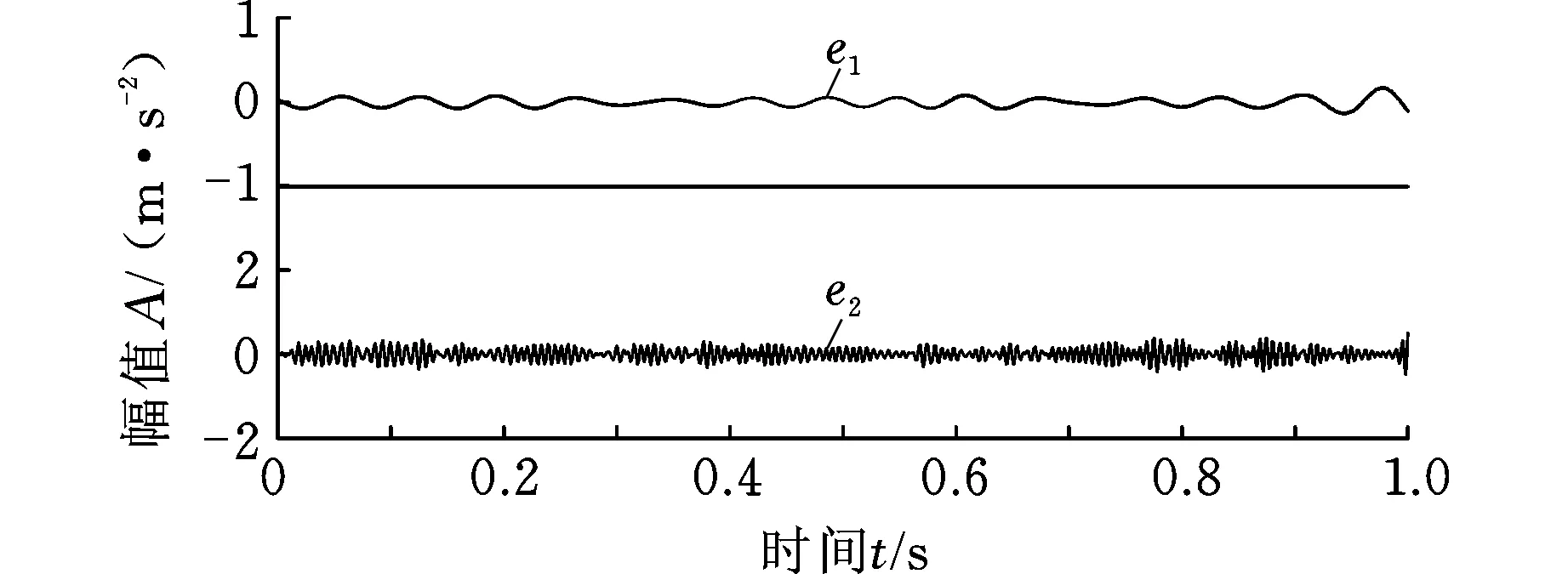
图5 NMD信号分解结果各分量误差曲线Fig.5 The error curves for each components
对仿真信号各分量及EEMD、NMD分解得到的分量求基于Hilbert变换的时频谱,见图6~图8。时频谱以三维灰度图的形式对各分量的瞬时频率和瞬时幅值均进行了刻画,振幅以灰度级表示,点越亮,振幅越大。由IMF分量的时频谱中可以看出,IMF分量在15 Hz附近能量比较集中,而在150~200 Hz能量分散,即EEMD只能分解出仿真信号的第一个分量。由NM分量的时频谱可以看出,NM分量与仿真信号分量的时频谱几乎一样。因此,与EEMD相比,NMD确实有一定的优越性。

图6 仿真信号各分量的时频谱Fig.6 Time-frequency spectrum of simulation signal components

图7 IMF分量的时频谱Fig.7 Time-frequency spectrum of IMF components

图8 NM分量的时频谱Fig.8 Time-frequency spectrum of NM components
3 齿轮箱复合故障诊断实验分析
为了验证NMD在实际应用中的可行性,将该方法用于实际旋转机械复合故障诊断中。通过激光切割的方式在齿轮和轴承上设置混合故障。滚动轴承的型号为SKF6307-2RS,在轴承的外圈上切割宽0.15 mm、深0.2 mm的槽来模拟轴承故障。齿轮的齿数为37,在齿轮上切掉一个齿来模拟断齿故障。实验中通过加速度传感器采集振动信号,采样频率fs=8192 Hz,采样时间为1 s。轴的转速为600 r/min,即转频fr=10 Hz,经计算滚动轴承外圈故障特征频率fo=31 Hz。
将采集到的故障信号(图9)进行包络谱分析,得到的结果见图10,从其包络谱可以看出,复合故障信号中的轴承外圈故障特征明显,但是齿轮故障特征被其他信号所淹没,无法判断齿轮是否发生故障。对复合故障信号进行NMD分解,得到3个NM分量(NM1、NM2和NM3),其时域波形见图11。对这3个分量进行包络谱分析,得到其谱图,见图12。
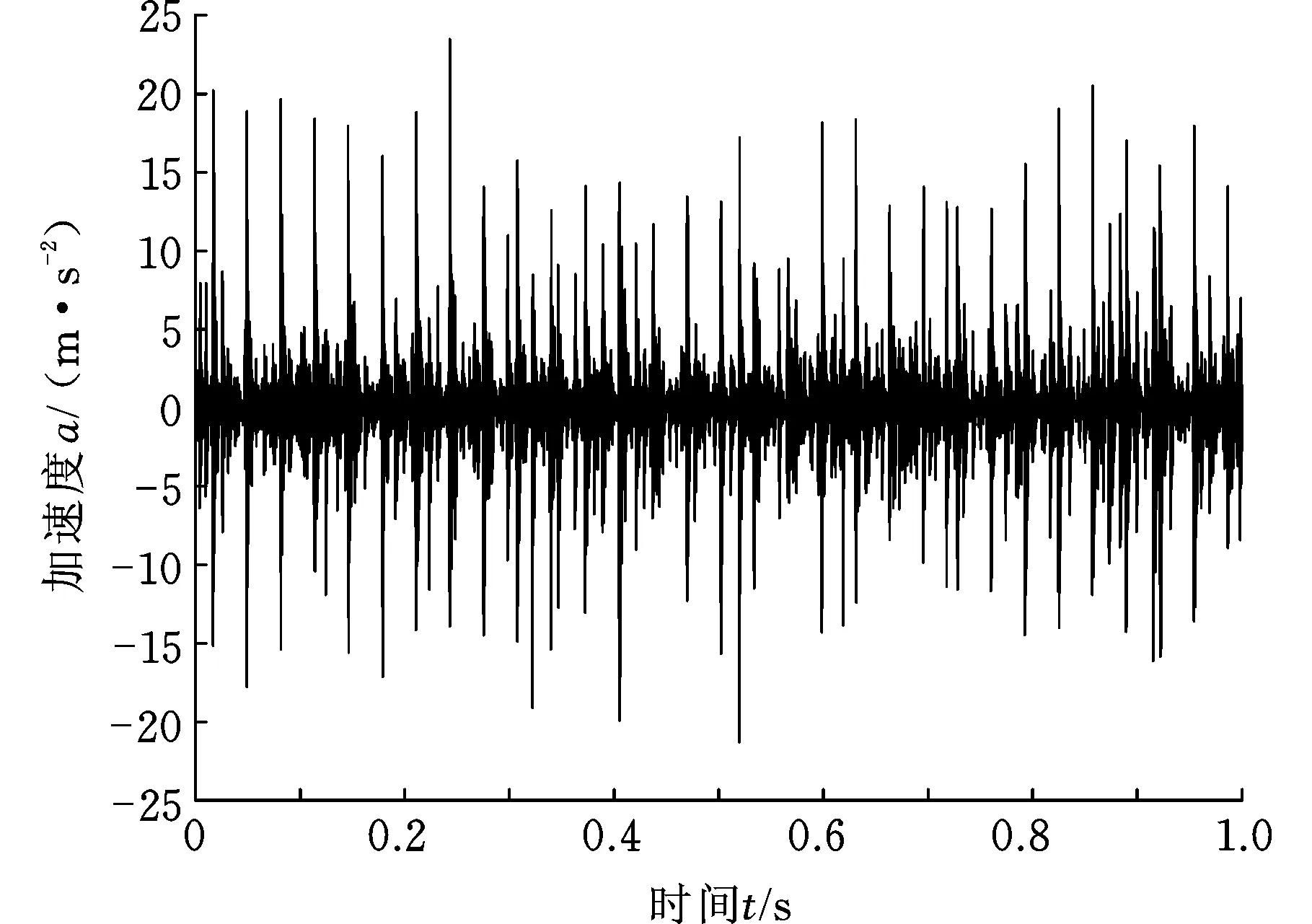
图9 复合故障信号时域波形Fig.9 Time domain waveform of composite faults signal

图10 复合故障信号包络谱Fig.10 Envelop spectrum of composite faults signal

图11 NM分量的时域波形图Fig.11 Time domain waveforms of NM components
由图12可以看出,NM1分量经过包络解调后,在转频fr及其倍频处谱线清晰可见,这与齿轮故障特征相吻合。在NM2分量的包络谱中存在一条很明显的谱线,且频率正好是外圈故障特征频率fo,NM3分量的包络谱在fo及其倍频处也存在明显的谱线,由此可以说明,该方法既可以把复合故障信号中的轴承故障特征提取出来,也可以将低频的齿轮故障特征提取出来,这就为NMD方法用于旋转机械复合故障诊断提供了有效依据。

图12 NM分量的包络谱Fig.12 Envelop spectrums of NM components
4 结语
针对旋转机械复合故障难以全面诊断的问题,本文提出了基于NMD的复合故障诊断特征提取方法。运用仿真信号将NMD与EEMD进行对比分析,结果表明,NMD既保证了所得分量都具有实际物理意义,又减少了所得分量的个数,同时还具有极强的噪声鲁棒性。对齿轮-轴承复合故障实测信号分结果析表明,基于NMD的特征提取方法能有效分离齿轮裂纹和轴承故障特征,证明了该方法的有效性和可行性。

