基于扩展G′/G-展开法的两个非线性拟抛物型方程的精确解

范 凯 ， 刘 斌， 宋叔尼， 范圆圆

(1. 太原科技大学 应用科学学院, 山西 太原 030024； 2. 东北大学 理学院， 辽宁 沈阳 110819)

拟抛物型方程是一类含时间和空间的混合偏导数的高阶偏微分方程， 出现在数学和物理的许多领域， 比如， 流体穿过缝隙岩石的渗透理论、 粘土的加固理论、 二阶流体的剪切变流、 热力学和小振幅的长波传播[1-4]. 广义的Benjamin-Bona-Mahony-Burgers(BBMB)方程

ut-uxxt-αuxx+γux+f(u)x=0,(1)

就是一个重要的拟抛物型方程， 其中，α>0，γ∈R,u=u(x,t)表示流体在水平方向x上的速度，f(u)∈C2-非线性泛函. 若在方程(1)中取f(u)x=θuux+βuxxx， 就可以得到了一个广义的Benjamin-Bona-Mahony-Peregrine-Burgers(BBMPB)方程

ut-uxxt-αuxx+γux+θuux+βuxxx=0,(2)

在方程(2)中取α=β=0， 就可以得到广义的Benjamin-Bona-Mahoney(BBM)方程

ut-uxxt+γux+θuux=0,(3)

式中：γ,θ为常数， 且θ≠0， 这就是众所周知的非线性色散系统长波传播的模型方程. 方程(2)包括几种类型的BBM方程， 方程(3)行波解的获得方法可参看文献[5-7]. 本文使用扩展G′/G-展开法研究BBMPB方程， 获得一些新的精确行波解， 延伸前人的工作.

在方程(2)取β=0， 得到一个广义的 Oskolkov-Benjamin-Bona-Mahony-Burgers(OBBMB)方程

ut-uxxt-αuxx+γux+θuux=0.(4)

方程(4)这个非线性拟抛物方程描述沿x轴传播的表面波， 其中，θuux表示粘性项[8-9]. 精确行波解的获得有助于更好地理解非线性偏微分方程所描述物理现象. 随着基于计算机代数系统的非线性科学的快速发展， 许多有效寻找非线性偏微分方程精确行波解的方法被提出， 例如齐次平衡法[10]、 sine-cosine方法[11]、 tanh函数法[12]、 扩展的tanh函数法[13-15]、 Exp-函数展开法[16]、(G′/G)-函数展开法[17-18]等. 本文使用简洁的扩展G′/G-展开法[19-20]获得方程(4)的新行波精确解.

1 扩展的G′/G-函数展开法

考虑一个以u(x,t)为未知函数的一般形式的非线性偏微分方程

P(u,ut,ux,utt,uxt,uxx,…)=0.(5)

下标t和x表示u(x,t)对t和x的偏导数.

扩展的G′/G-函数展开法求解非线性偏微分方程的步骤如下：

1) 做行波变化u(x,t)=U(ξ),ξ=x-vt， 把偏微分方程P(u,ut,ux,utt,uxt,uxx,…)=0转化为常微分方程

P(U,-vU′,U′,v2U″,-vU″,U″,…)=0.(6)

如果得到的方程(6)每一项都含有ξ的导数， 则可把这个方程先关于ξ积分， 令积分常数为零得到一个更为简单的方程.

2)假设方程(6)的行波解可拟设为如下形式:

(7)

式中：ai(i=0,1,…,m)和bi(i=1,2,…,m)都是待定常数. 参数m一般都为正整数， 平衡方程(6)中的最高阶导数项和最高阶非线性项的幂次可以确定m的值.G=G(ξ)满足如下常微分方程

G″+λG′+μG=0,(8)

式中：λ和μ是将被确定的常数.

3) 把式(7)代入式(6)， 收集(G′/G)各幂次的系数并令为0， 得到ai,bi,λ,μ,v的一个超定代数方程组.

4) 使用maple17求解这个超定代数方程组， 把ai,bi,λ,μ,v和G′/G的结果代入式(7)， 得到拟设形式的行波解.

二阶常微分方程(8)的通解形式(第一形式)整理如下

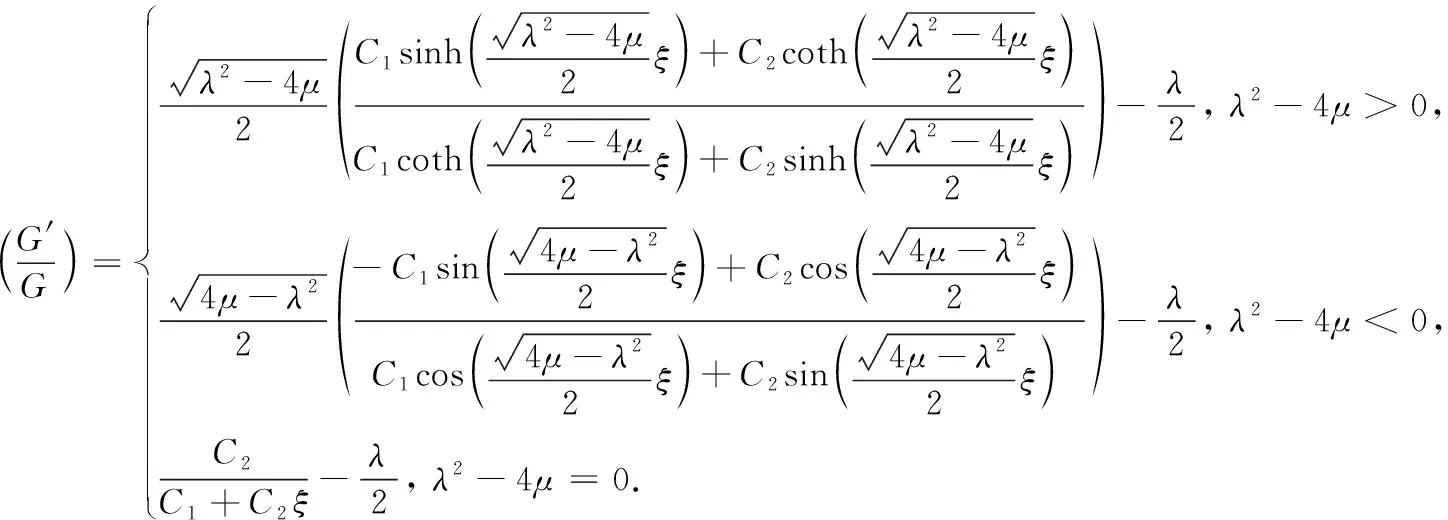
如果C1,C2满足相应的比例关系， 这些解可以化为更简便的形式(第二形式)如下

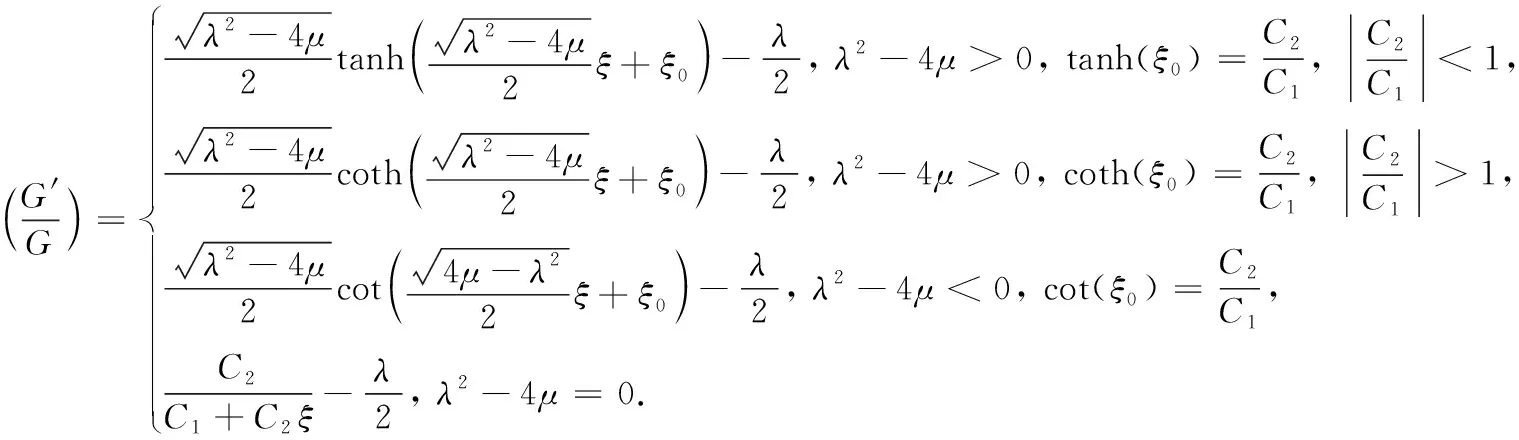
2 扩展的G′/G-函数展开法求解OBBMB和BBMPB方程

2.1 Oskolkov-Benjamin-Bona-Mahony-Burgers方程

OBBMB方程如下

ut-uxxt-αuxx+γux+θuux=0,(11)

式中：α为一个正数；θ为非零实数. 应用变换U(t,x)=U(z),z=x-vt， 把方程(11)转化为如下常微分方程

(12)

用平衡原理， 平衡U″和U2， 得到m=2， 所以方程(12)的解可拟设为

(13)

把式(13)代入式(12)， 收集G′/G各幂次的系数， 并都令为0， 得到一个超定代数方程组

用maple17求解这个超定代数方程组， 得到

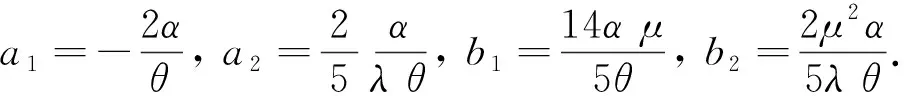
把式(14)的结果和二阶常微分方程(8)的解(第一形式)代入式(13)， 得到3种行波解,

1) 当λ2-4μ>0时， 得到双曲行波解

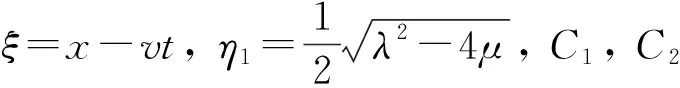
使用二阶常微分方程(8)的解(第二形式)， 双曲行波解U1(ξ)变为如下形式

当|C2/C1|<1,ξ0=tanh-1(C2/C1).

当|C2/C1|>1,ξ0=coth-1(C2/C1).

2) 当λ2-4μ<0时， 得到三角函数解

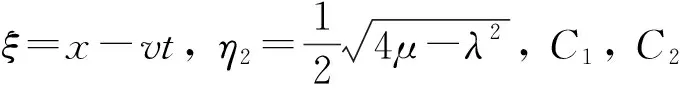
3) 当λ2-4μ=0时， 得到有理函数解

其中，ξ=x-vt，C1,C2是任意常数.

2.2 Benjamin-Bona-Mahony-Peregrine-Burgers方程

BBMPB方程如下

ut-uxxt-αuxx+γux+θuux+βuxxx=0,(15)

式中：α是一个正数；θ,β为非零实数. 应用变换U(t,x)=U(z),z=x-vt， 把方程(15)转化为如下常微分方程

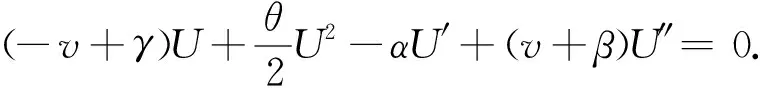
用平衡原理， 平衡U″和U2， 得到m=2， 所以方程(16)的解可拟设为

(17)

类似OBBMB方程的求解， 使用Maple17， 得到

把式(18)的结果和二阶常微分方程(8)的解(第一形式)代入式(17)得到3种行波解

1) 当λ2-4μ>0时， 得到双曲行波解

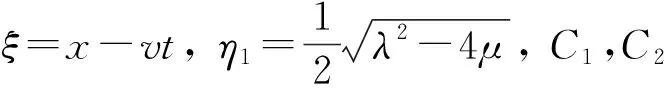
2) 当λ2-4μ<0时， 得到三角函数解

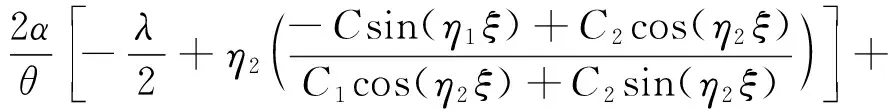
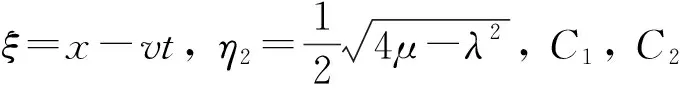
3) 当λ2-4μ=0时， 得到有理函数解

其中，ξ=x-vt，C1,C2是任意常数. 容易发现， 如果令BBMPB方程的精确解中的参数β为0， 这些解就变成了OBBMB方程的解， 这也佐证了本文解得正确性.

3 精确解的物理结果

本节对参数赋值， 给出了非线性拟抛物方程部分精确解的图示. 非线性拟抛物方程精确解的获得， 不仅有其物理意义， 也有助于这类方程数值解准确性的核对和稳定性的分析.

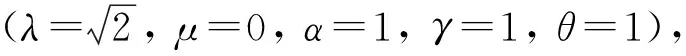
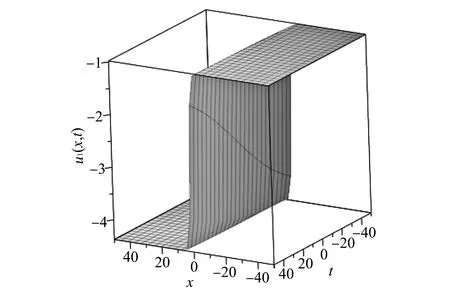
图 1 当时，OBBMB方程解 u1(x,t)的三维图Fig.1 3D plot of OBBMB equation u1(x,t) when

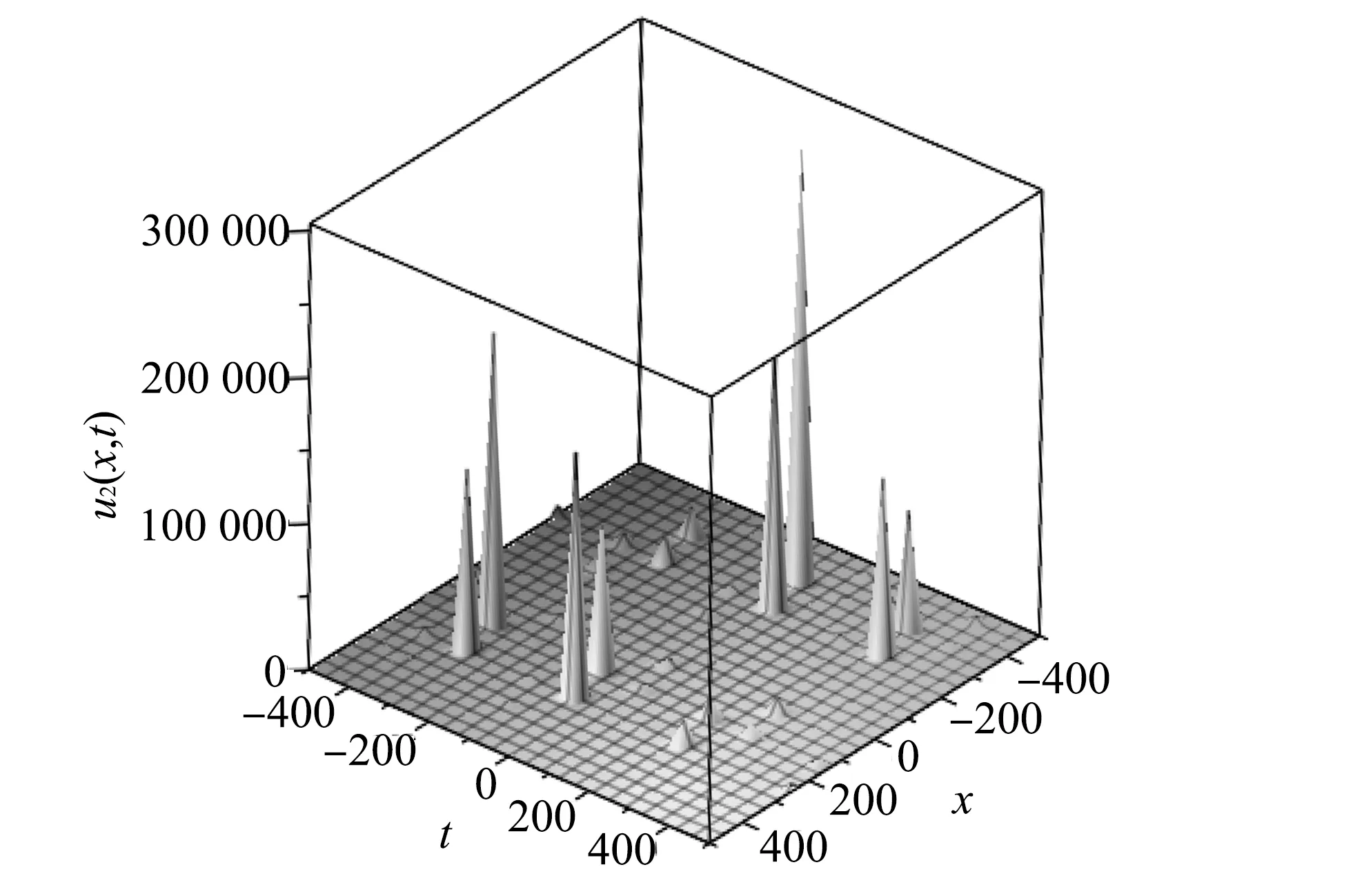
图 2 当时，OBBMB方程解 u2(x,t)的三维图Fig.2 3D plot of OBBMB equation u2(x,t) when

4 结 论

本文应用扩展的G′/G-函数展开法求解OBBMB和BBMPB方程， 分别得到它们含两个参数的3种类型的精确行波解， 通过对比两个方程和它们解， 验证了它们的正确性， 其中双曲函数类型的行波解在文献[15]中有类似的结果， 但三角函数类和有理函数类行波解是本文用扩展的G′/G-函数展开法求所得到的新类型的解， 并对部分解做三维图示， 简单解析了它们的物理结果. 本文所给的方法， 在maple的帮助下， 求解过程简单、 直接. OBBMB和BBMPB方程精确解的获得， 为该类型方程数值解的研究提供了一定的参考. 所满足的常微分方程还可以进一步优化， 以便我们得到更多的新的精确解， 有关这方面的研究结果， 我们将在其它文章中给出.