基于深度强化学习的追逃博弈算法*
谭 浪 巩庆海 王会霞
1.北京航天自动控制研究所,北京100854 2.宇航智能控制技术国家级重点实验室,北京 100854
远距离非接触式的精确打击已成为现代军事作战的主要手段,为提高导弹作战效能,导弹攻防对抗已成为现代军事研究的主要问题。在导弹攻防对抗中,进攻弹和拦截器具有相反的作战目的:进攻弹为逃逸者,为达成作战目的需要尽量躲避拦截器,而拦截器为追捕者,需要使目标处于杀伤或捕获范围之内,双方构成追逃博弈[1]。
目前,导弹攻防对抗的大多研究都是从经典控制方法出发,通过建立攻防双方微分对策模型,设计制导律来提高导弹武器的作战效能。例如,文献[2]通过对比例导引进行改进,使用卡尔曼滤波算法估计地方飞行信息,并使用姿态搜索算法以确定弹头的机动方向;文献[3]通过建立追逃对策模型,使用配点法对其进行求解,得到机动策略。文献[4]将导弹抽象为智能体,从多智能体系统的角度研究攻防对抗问题,但仅用以解决仿真中时空不一致的问题,并没有从智能算法的角度研究导弹攻防对抗过程。
随着人工智能技术的飞速发展,各国正致力于研究智能化程度更高的导弹和武器系统来替代现有的设计方案[5]。当AlphaGo在围棋领域击败人类顶尖选手时,深度强化学习已经成为备受学者们关注的研究热点[6-7]。深度强化学习技术被认为是最有可能实现通用人工智能计算的重要途径之一,具有很强的通用性。目前深度强化学习在经典控制领域的应用是OpenAI公司使用深度Q网络(Deep Q Network, DQN)算法在模拟环境gym下对倒立摆进行了稳定控制[8]。此外,在真实场景下的应用是使用近端策略优化(Proximal Policy Optimization, PPO)算法对机械臂控制,使其完成抓取木块的操作[9]。
用三维空间中的导弹攻防问题抽象为二维平面中智能小车的追逃问题,在DDPG算法[10]的基础上提出一种追逃博弈算法。该算法的回报函数采用PID控制的思想进行设计,并在Epuck小型移动机器人上进行了追逃博弈实验验证。算法以定位系统获得的位置信息作为输入,通过对神经网络进行训练,输出追捕者的控制指令,控制其最终成功地完成追捕任务。
1 追逃博弈模型
一对一追逃博弈场景分为一个逃跑者和一个追捕者,它们具有相反的目的:逃跑者要躲避追踪,而追捕者要捕获逃跑者。
一对一追逃博弈模型如图1所示:
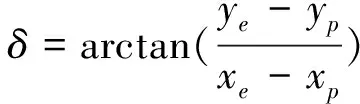
追捕者与逃跑者的运动学模型为:
(1)
式中:i是指追捕者P和逃跑者E;(xi,yi)是智能小车的位置;θi是方向;ui是转向角,ui∈[-uimax,uimax];vi是由转向角控制的智能小车的速度;φi表示速度方向与视线角的偏差。
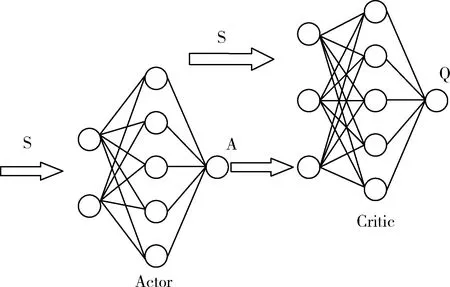
在图1所示的追逃博弈模型中,设定追捕者应快于逃跑者,即vpmax>vemax,但同时追捕者的机动能力比逃跑者差,即upmax 马尔科夫决策过程(Markov Decision Process , MDP)由一个五元组(S,A,T,R,γ)描述[11],其中:S为有限的状态空间;A为有限的行为空间;T为状态转移函数;R为回报函数;γ为折扣因子。转移函数表示在给定当前状态和行为下,转移到下一状态的概率分布: (2) 式中:s′表示下一时刻的可能状态。 回报函数表示给定当前行为和状态下,在下一状态得到的回报。马尔科夫决策过程具有如下的马尔科夫特性:智能体的下一时刻的状态和回报仅取决于智能体在当前时刻的状态和行为。 在任一马尔科夫决策过程中,智能体都存在一个确定的最优策略,强化学习的目标就是寻找给定的马尔科夫决策过程中的最优策略。 强化学习是智能体自主探索环境状态,采取行为作用于环境并从环境中获得回报的过程。一般而言,强化学习问题是建立在马尔科夫决策过程模型的基础上。 图2 强化学习框架 强化学习框架如图2所示。智能体在当前状态s下,采取行为a,根据状态转移函数T,环境会转移到下一状态s′,同时环境会对智能体反馈一个奖励信号,即回报r。智能体在下一状态按照上述过程依次进行。智能体的目标是通过不断地训练,获得最大化的长期回报。为评估智能体策略,定义状态值函数Vπ(s)为:当智能体从状态s开始并随后执行策略π时,在该策略下状态的值。因此: (3) 式中:T为最终时刻;t为当前时刻;rt+1为在t+1时刻得到的回报。 由图2可知,环境反馈给智能体的回报r与状态s和动作a有关,可用价值函数来描述之间的关系。定义行为值函数Qπ(s,a)为:当智能体从状态s选择特定行为a并随后执行策略π而得到的预期回报。一个最优策略π*将使得智能体在所有状态下可获得最大化的折扣未来回报。则在最优策略下的行为值函数Q*(s,a)可重写为一个贝尔曼最优方程: (4) 对于图1所示的智能小车追逃博弈场景而言,环境的状态及智能体的动作都是连续量。因此,使用深度学习中的神经网络构造函数逼近器,得到近似的行为值函数。Q值神经网络定义为: Q(s,a)≈f(s,a,w) (5) 式中:w是指神经网络的参数。 以深度强化学习中的DDPG算法为基础,定义MDP状态空间与行为空间,设计回报函数,从而实现智能小车的控制算法,用以对追捕者进行导航与控制,使其尽可能快地追上逃跑者。 通过使用定位系统实时获得各智能小车的位置信息,以此为基础构造输入神经网络的状态量。对于图1所示的追逃博弈场景,本文算法的目的是最小化追捕者和逃跑者之间的相对距离。因此,给出MDP状态空间如下: S=[L,δ]T (6) 在本文第1节所设定的追逃博弈场景中,逃跑者的状态可以是静止、匀速直线运动或带有机动的运动(即角速度不为0)。追捕者的策略是由神经网络的输出给定。因此,给出MDP动作空间为up。更近一步,由式(1)可知,追捕者转向角影响的是追捕者的角速度,因此,动作空间为: (7) 对于追逃博弈场景而言,MDP转移函数即为各智能小车的运动学方程,即式(1)。 追捕者的目的是成功捕获逃跑者,由于实验场地的限制,追捕者不能越过边界,否则认为追捕任务失败。因此,在最终时刻,如果追捕任务成功,则给予一个较大的正回报,否则给予一个较大的负回报。对于在追捕任务过程中的回报函数的设计,借鉴PID控制思想,即:如果追捕者的速度方向与视线相同,则追捕者一定能成功追捕逃跑者(因为追捕者速度大于逃跑者)。因此,追捕任务过程中的回报定义为:kφp。综上所述,MDP回报函数设计如下: (8) 式中:k是比例因子。 本文采取强化学习中的异策略(off-policy)学习方法,神经网络的架构采用AC(Actor-Critic Algorithm)的方法,即使用Actor网络得到行为策略,使用Critic网络得到评估策略。Actor-Critic 网络结构如图3所示。 由于定位系统得到的智能小车的位置信息是一个在时间上连续的序列,因此由状态构成的样本之间并不具备独立性。为解决这个问题,本文算法使用了经验回放和独立的目标网络。经验回放即将样本存储在经验池中,并在经验池达到一定程度后随机从中选取若干样本进行训练。使用独立的目标网络即再使用一个与策略网络结构一样的AC网络。 图3 Actor-Critic网络结构 神经网络的训练过程实质上是通过构造一个代价函数,对其进行梯度下降,从而可得到最优的神经网络参数。Actor网络输出的是智能体的行为策略,Critic网络输出该行为的评估。因此,Critic网络的代价函数如下: Li=E[(yi-Q(si,ai|θQ))2] (9) 式中:yi=E[ri+γQ′(si+1,μ′(si+1|θμ′)|θQ′)]。 Actor网络的策略梯度为: (10) 目标网络采用延迟更新的方式,即一定时间后将目标网络参数替换为策略网络的参数。 智能小车追逃博弈算法如表1所示。 本文采用的智能小车是由瑞士联合科技院研制的Epuck小型移动机器人,具体构造如图4所示。Epuck智能小车由DSPIC处理器驱动,车身一周覆盖有8个红外距离传感器,可测量传感器前方6cm的物体,并且集成了VGA彩色摄像头和8个LED。此外,智能小车可配备扩展板,通过WiFi与计算机和其他智能小车间通讯。本文对于智能小车的具体型号并不做严格要求,其仅作为本文算法验证的执行机构。 表1 追逃博弈算法 图4 Epuck移动机器人 小车的室内定位系统采用的是运动捕捉系统,定位精度不低于1mm。定位系统实时获取智能小车的位置并传输到上位机,上位机通过计算得到状态量,并将其输入到神经网络,经训练得到追捕者小车的控制策略,然后将指令通过无线传输到追捕者小车以控制其进行追捕任务。 本文算法程序基于Python语言进行编程,以深度学习框架TensorFlow为基础,算法中的神经网络均采用全连接网络的架构,网络采用2个隐含层,分别有150和50个节点,训练算法的minibach设置为16,经验池大小为10000,学习率为0.0001,折扣因子为0.9,回报函数中的比例因子设置为2。其它实验参数如表2所示: 表2 实验参数 训练时,逃跑者做匀速直线运动,算法训练500次,记录每次的累积回报,结果如图5所示。由图5可知算法在训练约100次时开始收敛。图6分别显示了两智能小车在训练前和算法收敛时的运行轨迹图,可以看出训练前追捕者小车处于没有策略的运动状态,最终超出边界而导致任务失败;当算法收敛后,追捕者小车能够做出正确的决策,最终成功地捕获逃跑者。 图5 算法收敛趋势 图6 智能小车运行轨迹 为了验证本文算法的适应性,在评估时将小车的初始位姿进行修改,使其在一定的范围内随机分布,并进行100次测试评估。图7(a)显示了这100次评估对的累积回报值,图7(b)显示了最后一次的智能小车运行轨迹。由图7(a)可以看出,这100次评估实验中,追捕者小车均能成功捕获逃跑者小车。 此外,将逃跑者的运动状态分别更改为静止和随机运动,再次对算法进行评估,实验结果分别如图8和9所示。在这2种状态的评估实验中,追捕者小车均能成功完成任务,表明本文算法具有较强的适应性。 图7 算法评估结果 图8 逃跑者静止时小车运行轨迹 图9 逃跑者随机机动时小车运行轨迹 使用训练好的模型对追捕者小车进行控制,在室内场地进行实验,实验中分别将逃跑者小车的状态设置为静止、匀速直线运动和随机运动,模型输入追捕者小车的状态,输出控制指令,经WiFi传输给追捕者,控制追捕者运动。在这3种状态的Epuck小车追逃博弈实验中,追捕者均能够成功地捕获逃跑者,与上文对算法评估中的3种仿真实验结果一致,表明算法能够实际地用在对智能小车的导航控制中。 立足于三维空间中导弹的攻防对抗问题,将其抽象成二维平面的小车追逃博弈,提出了基于深度强化学习的追逃博弈算法。算法以DDPG算法为原型,设计针对智能体追逃的马尔科夫决策过程中的状态空间、动作空间和回报函数,并对算法进行训练,收敛后的模型在数学仿真和实物实验中均成功地实现追捕任务。实验结果表明本文所提出的深度强化学习算法可以有效地实现对智能小车的导航与控制,具有较强的适应性。后续,可将智能小车的运动模型替换为导弹的运动学和动力学模型,用以研究和仿真三维空间的导弹攻防对抗过程。2 马尔科夫决策过程与强化学习
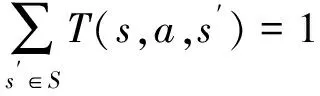

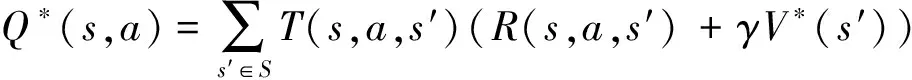
3 追逃博弈算法设计
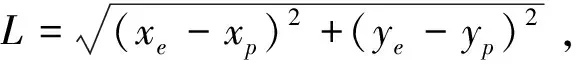

4 实验验证
4.1 实验平台


4.2 实验参数设置

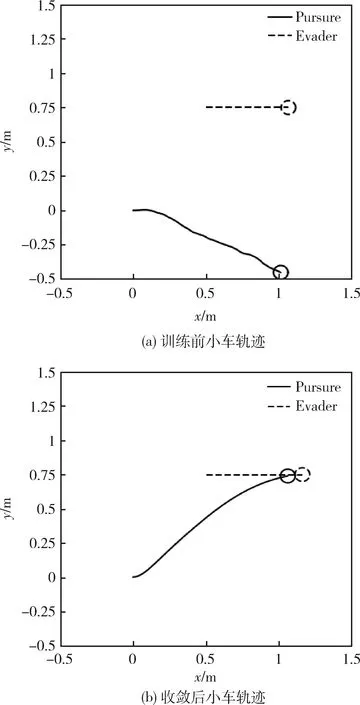
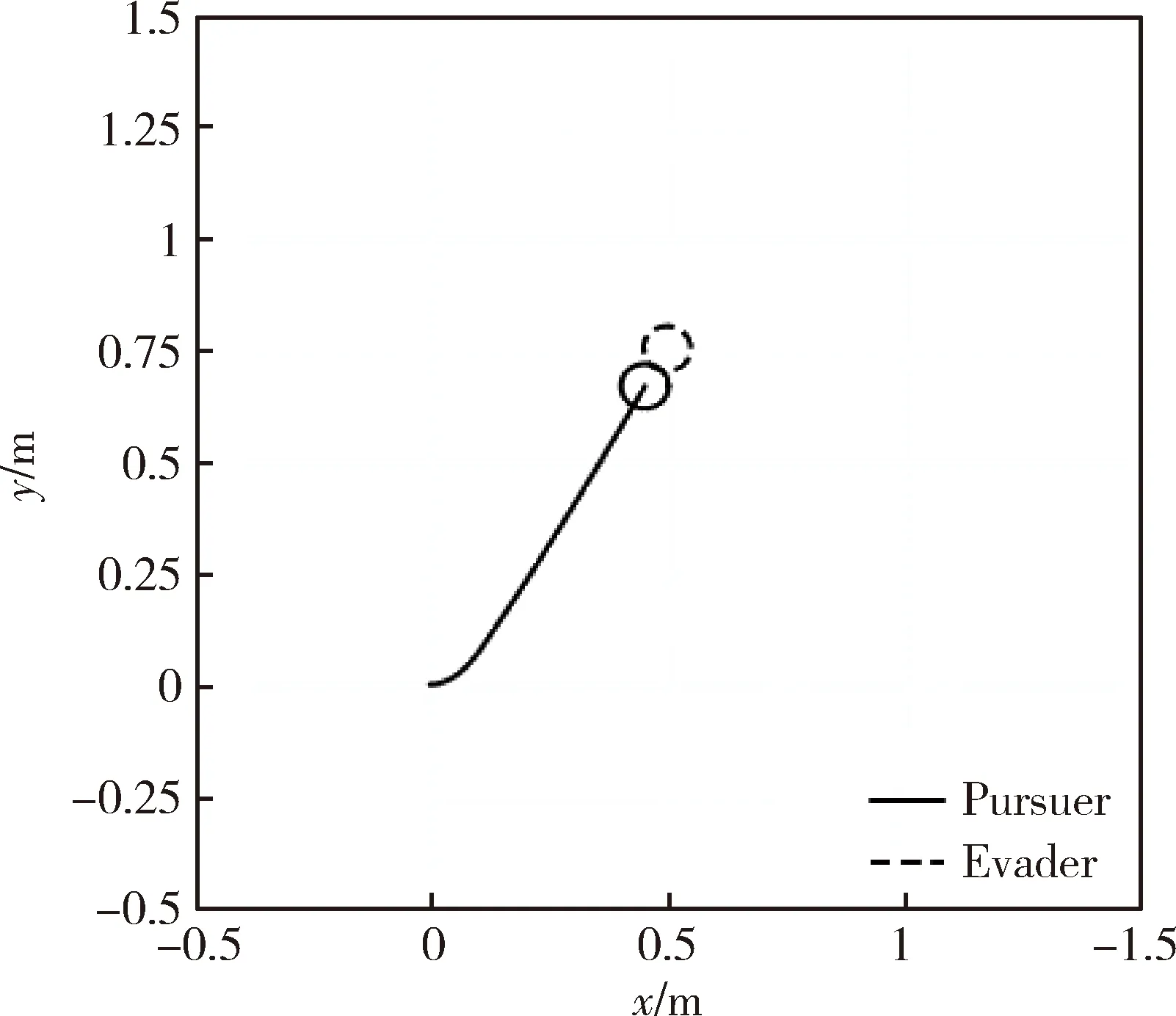
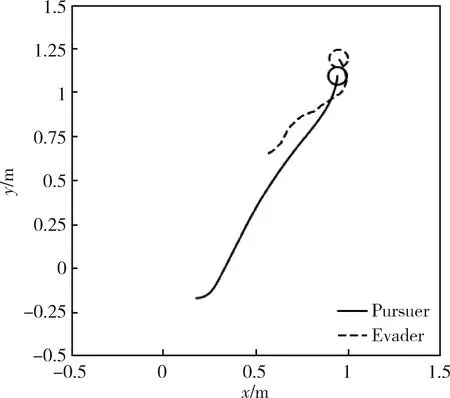
4.3 实验结果分析


5 结论

