考虑终端姿态约束的自适应迭代制导方法
郝钏钏 司 成 周曼娟
上海宇航系统工程研究所,上海 201109
随着现代计算机技术和最优控制理论的发展,也为了适应空间发射任务多样化、复杂化的现实需求,迭代制导方法在运载火箭上得到越来越广泛的应用。美国的“土星”火箭和欧空局的“阿里安”火箭以及我国新一代运载火箭均采用了迭代制导技术[1-3]。
迭代制导技术通过调整火箭飞行姿态控制其质心运动,为克服飞行过程中各种干扰的影响,会造成主动段终端姿态散布较大,姿态偏差指标设计值可能会超过20[2]。由于有效载荷对入轨姿态精度要求较高,对于没有配备姿控发动机系统的火箭,迭代制导会带来较大的入轨姿态偏差;对于配备姿控发动机系统的火箭,迭代制导引起的主动段终端姿态偏差需要额外的星箭分离前姿态调整时间来克服,而这往往需要进行飞行弹道调整以满足本就比较紧张的“星箭分离后卫星有效测控时间”需求,这也必然会导致一定的运载能力损失。
为了同时满足轨道参数约束和终端姿态约束,文献[4]提出一种在线轨迹预测制导方法,以不考虑终端姿态约束的迭代制导姿态最优解为初值,根据数值积分预测的火箭运动轨迹对最优姿态进行反馈迭代优化;但该方法的复杂度和计算量远大于经典迭代制导方法。文献[5]提出一种基于联立框架的直接法在线轨迹规划方法,利用有限元正交配置进行低阶逼近和联立求解,能同时满足入轨精度和终端大姿态约束,但方法亚秒级的求解时间限制了其应用。
受文献[6]提出的一种通过在线估计火箭实际入轨点的纬度幅角进行制导目标点调整以精确控制近地点幅角的改进迭代制导方法的启发,同时借鉴嫦娥三号着陆器动力下降段的制导控制方法[7],本文提出一种考虑终端姿态约束的自适应迭代制导方法,在确保有效载荷精确入轨的同时满足主动段终端姿态约束。并通过某型三级火箭的仿真分析证明了方法的有效性。
1 迭代制导的基本原理
迭代制导算法以终端坐标系OE-XTYTZT为基本参考系,以地心OE为原点,OEYT轴指向预估实际关机点,OEZT轴垂直于轨道面并指向轨道动量矩方向,OEXT轴与OEYT轴和OEZT轴构成右手坐标系。
在真空段忽略滚动角时运载火箭的运动方程如式(1)所示
(1)
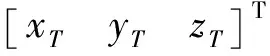
迭代制导方法以运载火箭瞬时状态为初值,以终端目标状态为终端约束,以火箭的一组姿态角为控制变量,以最短飞行时间为性能指标,构造汉密尔顿两点边值优化问题。在发动机推力平稳、地球引力场采用平均引力场近似等条件下,文献[8]给出了该最优控制问题的最优姿态如式(2)所示
(2)
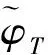
2 目标点自适应迭代制导方法
为了解决迭代制导引起的主动段终端姿态散布较大的问题,本文将火箭末级主动段按先后顺序分为迭代制导段和姿态快速调整段;在末级主动段结束前停止迭代制导进入姿态快速调整段,利用主发动机将火箭姿态调整至期望终端姿态;在迭代制导段的制导计算中,根据对姿态快速调整段影响的实时估计,自适应确定迭代制导段终端的目标状态。
2.1 迭代制导段终端目标状态自适应确定


(3)

2.2 迭代制导段终端姿态估计
迭代制导段的终端目标状态确定后,可以按照文献[8]中给出的经典迭代制导算法进行制导计算,计算迭代制导段的剩余飞行时间tk和如式(2)所示的解析形式的最优姿态角。
在工程实施上迭代制导往往采用分级制导方案,当剩余飞行时间小于某一数值tzp时,取消终端目标位置约束;当剩余飞行时间小于某一数值tzv(0 当tk>tzp时, (4) 运载火箭制导控制的基本坐标系为发射惯性系,它在火箭起飞瞬时与发射系重合。发射系以发射点为原点,OXa轴在当地水平面内并指向发射方向,OYa轴沿发射点重力反方向,OZa轴与OXa轴和OYa轴构成右手坐标系。 (5) 其中,β为如图1所示的预估主动段终端与理论主动段终端之间的地心角。 图1 预估主动段终端与理论主动段终端间的地心角示意图 参考经典迭代制导中β的计算方法[8],考虑本文算法中到主动段终端的剩余飞行时间(包括迭代制导段的剩余飞行时间tk和姿态快速调整段的飞行时间ttz),因此本文算法中β的计算方法如式(6)所示。 (6) 考虑到迭代制导段预估的剩余飞行时间是在对火箭运动方程作了简化处理后的计算结果,并且姿态快速调整段的开环飞行过程中会受到各种干扰的影响,为了确保实际飞行中主动段终端的姿态调整到并稳定在期望姿态,将姿态快速调整段的姿态变化规律设计成如式(7)所示。 (7) 其中,t*为相对姿态快速调整段开始时刻的时间,ttz1(ttz1 由于液体火箭发动机推力相对稳定、火箭质量变化缓慢连续,因此推力视加速度变化缓慢连续。考虑到姿态快速调整段的时间比较短,因此可以近似认为“整个姿态快速调整段的推力视加速度为固定值,数值上等于姿态快速调整段中间时刻的推力视加速度值”,见式(8) (8) 结合姿态快速调整段的姿态调整规律设计,姿态快速调整段的推力视速度增量计算如式(9)所示。 (9) 姿态快速调整段的推力视位置增量的精确计算公式比较复杂。考虑到位置动态相对于速度动态为慢动态,以及轨道参数对位置偏差的敏感度较低。因此姿态快速调整段的推力视位置增量可以用式(10)进行简化计算而不会对最终入轨精度产生太大影响。 (10) 由于迭代制导段的终端姿态估计会影响迭代制导段终端目标状态的确定,而迭代制导段终端目标状态又会影响迭代制导段的终端姿态估计,因此需要对迭代制导段的终端姿态估计值进行迭代计算。选择主动段终端的期望姿态作为其实际终端姿态的初始估计,考虑终端姿态约束的自适应迭代制导算法的计算流程为: 1)初始化:设置β=0,φTy(k)=φGs+90°,ψTy(k)=ψGs; 2)计算终端坐标系下的期望终端姿态:φTs=φGs+(90-β),ψTs=ψGs; 4)自适应确定迭代制导段终端目标状态; 5)用经典迭代制导计算迭代制导段的剩余飞行时间tk及实际终端姿态角φTy(k+1)和ψTy(k+1)估计值; 6)若迭代制导段的终端姿态估计值收敛:|φTy(k+1)-φTy(k)|≤ε,且|ψTy(k+1)-ψTy(k)|≤ε,则迭代结束;否则,返回步骤2)。 以某型三级液体运载火箭为例,对经典迭代制导算法和本文提出的考虑终端姿态约束的自适应迭代制导算法的制导控制效果进行仿真分析。二级飞行段均采用经典迭代制导算法,三级飞行段分别使用经典迭代制导算法和本文的迭代制导算法。选择三级关机点的期望终端姿态为:俯仰角为-41.267°,偏航角为-2.5°。 由经验和仿真结果可知,三级发动机秒耗量偏差对主动段终端姿态影响最大。在三级发动机秒耗量下降30%的情况下,2种迭代制导方案的仿真结果如表1所示。 表1 两种迭代制导方案在“三级秒耗量下降30%”时的结果 由表1可知,与经典迭代制导方案相比: 1)从入轨精度上看,采用本文的迭代制导方案时,半长轴偏差略大,但偏心率偏差和倾角偏差略小; 2)从三级发动机关机点的姿态偏差上看,采用本文的迭代制导方案时的姿态偏差为0°,而采用经典迭代制导方案时的俯仰角偏差达到11.120°,偏航角偏差为2.255°; 3)从三级关机时间偏差看,采用本文的迭代制导方案时,三级飞行段多飞行35ms,多消耗推进剂约1.2kg。 表明在“三级发动机秒耗量下降30%”的情况下,本文的迭代制导方案在略微增加推进剂消耗的情况下能很好地满足终端姿态约束,并且入轨精度与常规迭代制导方案基本相当。 2种迭代制导方案的三级飞行段俯仰、偏航姿态角对比分别如图2和3所示。2种迭代制导方案的三级飞行段中的迭代制导段的姿态角偏差曲线如图4所示。 图2 两种迭代制导方案的三级飞行段俯仰姿态角对比 图3 两种迭代制导方案的三级飞行段偏航姿态角对比 图4 两种迭代制导方案中迭代制导段的姿态角偏差 2种迭代制导方案的制导误差综合结果对比如表2所示。 由表2可知,采用本文的迭代制导方案时的入轨偏差与采用经典迭代制导方案时基本一致,但三级关机点的姿态偏差为0°。采用经典迭代制导方案时,三级关机点的俯仰姿态偏差达7.344°、偏航姿态偏差为1.432°。 提出一种考虑终端姿态约束的自适应迭代制导方法。将末级主动段分为迭代制导段和姿态快速调整段。通过在线估计姿态快速调整段的影响,自适应确定迭代制导段的终端目标状态;并在姿态快速调整段将姿态调整至期望值。该方法能同时满足轨道参数和终端姿态约束,仅增加少量推进剂消耗,有很强的工程实用价值。
2.3 终端坐标系下的期望终端姿态角计算

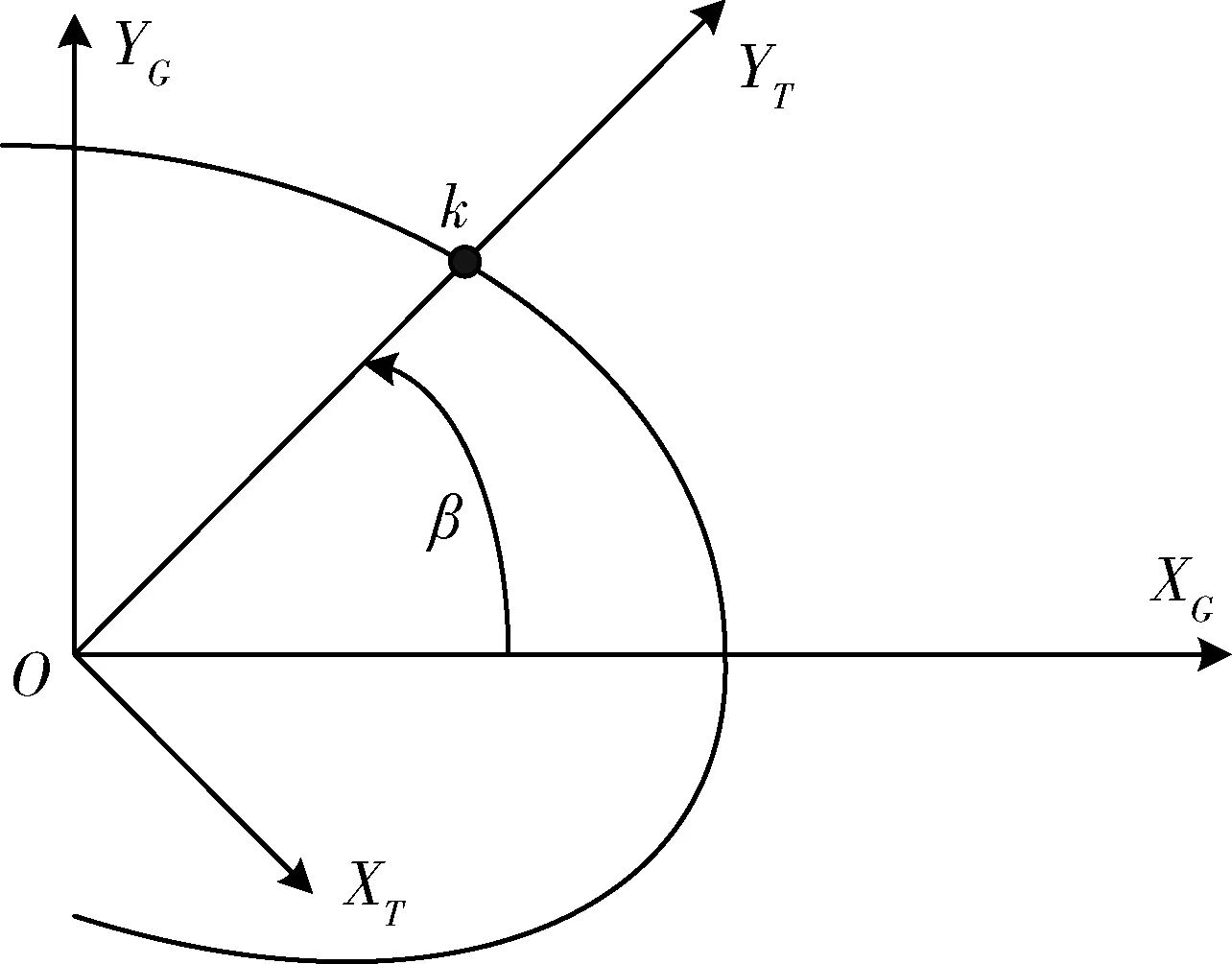
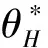
2.4 姿态快速调整段的姿态调整规律设计

2.5 姿态快速调整段推力视加速度影响估计
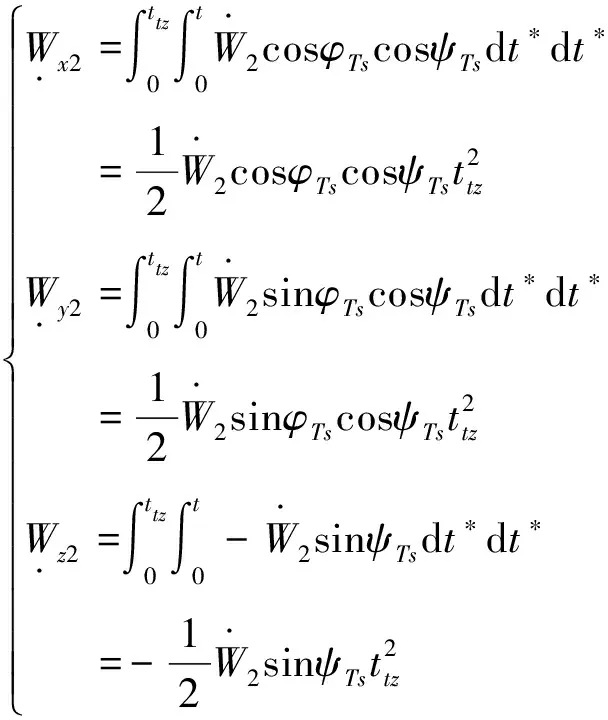
2.6 自适应迭代制导算法的计算流程

3 仿真分析




4 结论

