初等数论在数学竞赛及密码学中的应用
张本慧,崇金凤,卓泽朋
(淮北师范大学 数学科学学院,安徽 淮北 235000)
1 引言
《初等数论》[1-3]课程主要研究整数的运算规律.熟练掌握初等数论的基本内容(如整除理论、同余知识、不定方程、素数分布、数论函数等)、基本思想与基本方法,可以促进学生对整数性质的深入理解,强化分析问题、解决问题的能力,扩充知识的广度,培养发散思维,为学生学习《离散数学》和《近世代数》等课程奠定必要的基础.本课程是数学中最古老的分支之一,也是师范院校数学类各专业的一门专业选修课,它对于提高师范专业学生的教师素质具有十分重要的意义.
《初等数论》课程与中小学的数学竞赛紧密相连,如数学家罗曼在1959年发起的国际数学奥林匹克竞赛,经过五十多年的发展,它已经成为规模最大、类型多样、层次较高的一项学科竞赛.根据对奥林匹克数学竞赛题的统计,能直接利用数论知识解决的题目大约有30%,这还不包括那些解题过程与数论相关的题目.与数论相关的世界数学难题也有很多,如费马猜想[4]、哥德巴赫猜想[5]等.哥德巴赫猜想至今仍未完全解决,一批又一批的数学家们还在不断努力,这足以看出数论在数学领域的重要地位.《初等数论》课程并不是孤立的,它与其它学科也密切相关,如计算机科学、密码学等.本文结合笔者多年的教学经验和研究方向(密码学),谈谈数论在数学竞赛及密码学中的相关应用.
2 初等数论在数学竞赛中的应用
2.1 整除理论在数学竞赛中的应用
整除理论是初等数论的基础,它对中小学学过的整数运算规律进行了抽象系统的归纳总结,主要包括最大公约数理论和算术基本定理.在各类数学竞赛中,与整除理论有关的题目占有相当大的比例,下面通过具体的例子来说明如何借助整除理论解决数学竞赛题.
例1[6](第3届“希望杯”初一二试题)设a,b,c是三个两两互素的自然数,其中任意两个之和都能被第三个整除,求a3+b3+c3的值.
解不妨假设 a>b>c,则,又 b|(a+c),则 b|(b+c+c)⇒b|(b+2c)⇒b|2c,而 b,c 互素,故 b|2,又 b>c,从而 b=2,c=1,a=3,所以 a3+b3+c3=36.
例2[7](第4届奥数题)求满足下列性质的最小自然数n,其十进制表示法中以6结尾,如果把最后的6去掉并放在最前面所得到的数是n的4倍.
解n以6结尾,根据带余数除法有n=10m+6,其中m是正整数,设m的位数为l,根据题意有
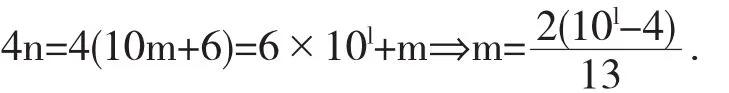
又m为正整数,则13|2(10l-4)⇒13|10l-4.要求最小的n,问题转化为求最小的正整数l,使得13|10l-4.取l=1,2,…,,逐个验证求得满足条件的最小的l=5,从而m=15384,于是所求的最小自然数n=15384.
例3[8](2006年全国初中数学联赛试题)已知0<a<1 且满足

求[10a]的值.
解由于等于 0 或 1,由题意知,这其中有18个等于1,从而
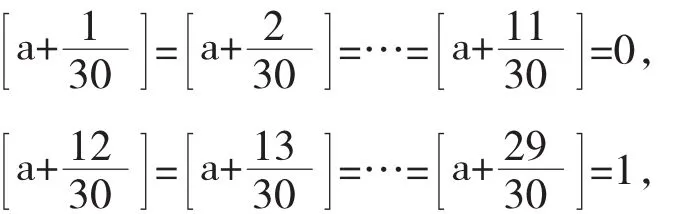
2.2 同余理论在数学竞赛中的应用
首先看这样一个问题(Q):假设今天是星期一,那么从今天起再过101010天是星期几?
这个问题看似很复杂,但是如果从同余的角度来解决这个问题就非常简单.同余是数论中的一个基本概念,它是研究整数问题的重要工具,在各类数学竞赛中也有广泛的应用.
定义1[1]设m是正整数,如果m|(a-b),则称a同余于 b 模 m,记作 a≡b(modm),如果 m■(a-b),则称a不同余于b模b,记作a≢b(modm).
可以这样回答问题(Q):106≡1(mod7),1010≡(-2)10≡322≡22≡4(mod6),假设 1010=4+6k,其中 k为正整数,则101010=104+6k≡104≡4(mod7),所以再过101010
天是星期五.
例4[8](2012年数学周报杯全国初中数学联赛试题) 假设n是整数且1≤n≤2012,求满足(n2-n+3)(n2+n+3)能被5整除的所有n的个数.
解首先,(n2-n+3)(n2+n+3)=(n2+3)2-n2=n4+5n2+9,又 5|(n2-n+3)(n2+n+3),故 5|(n4+9),从而 n4≡1(mod5),于是5不能整除n,又2012÷5=402余2,2012-402=1610,即满足条件的n共有1610个.
例5[7](第六届奥数题)1)求能使2n-1被7整除的所有正整数n;2)证明:对任意正整数n来说,2n+1都不能被7整除.
解对任意正整数n,根据带余数除法,存在整数q,r使得n=6q+r,其中0≤r≤5,从而根据费马小定理有,2n±1=26q+r±1=(26)q·2r±1≡2r±1(mod7),r取0,1,2,3,4,5.
1)当 r=0.3 时,即 n=6q 或 n=6q+3,此时 2n-1≡2r-1≡0(mod7),也就是说,当且仅当3|n时有7|(2n-1).
2)不论r取0,1,2,3,4,5中的哪一个,都有2n+1≡2r+1≢0(mod7),也就是说,对任意正整数 n,2n+1都不能被7整除.
2.3 数学竞赛中的不定方程
未知数的个数多于方程个数,且未知数取整数的方程称为不定方程.在各类数学竞赛中不定方程的问题经常出现.
定义2[1]称a1x1+…+akxk=c为k元一次不定方程,这里整数 k≥2,c,a1,…,ak是整数且 a1,…,ak非零.
例6[8](2012年全国初中数学联赛试题)求各边长为整数且周长为60的直角三角形的外接圆面积.
解设三条边长分别为a,b,c,不妨设a≤b<c,由于周长为 60且 a+b>c,则

又 a2+b2=c2,将 c=60-a-b 代入,得
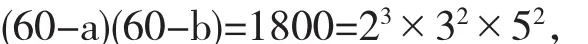
由于 a≤b<c<30,
故 30<60-a<60,30<60-b<60,60-b≤60-a,从而
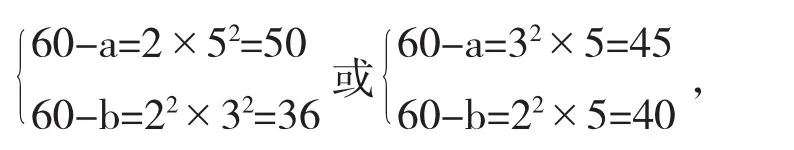
3 初等数论在密码学中的应用
密码学的基本目的是使得两个在不安全信道中通信的人,以一种使他们的敌人不能明白和理解通信内容的方式进行通信.很多密码协议的设计都是以数论知识为基础,如移位密码、RSA密码协议等.
3.1 移位密码
移位密码[9]是古典密码中的一种,其理论基础是数论中的模运算.

表1 移位密码
建立26个英文字母和模26剩余之间的一一对应关系,如a↔0,b↔1,…,z↔25,然后利用移位密码就可以加密英文句子,下面介绍例7.
例7设移位密码的密钥为K=11,明文为wewillmeetatmidnight
写出明文中的字母对应的整数,得:22/4/22/8/11/11/12/4/4/19/0/19/12/8/3/13/8/6/7/19
将每个整数与11相加并作模26运算,得:7/15/7/19/22/22/23/15/15/4/11/4/23/19/14/24/19/17/18/4
写出每个整数对应的字母,得到密文为:hphtwwxppelextoytrse
要对密文解密,只需执行逆过程.
3.2 RSA密码协议
1977 年,Rivest、Shamir和 Adleman 设计了著名的RSA密码协议[9],其理论基础是欧拉定理.
欧拉定理[1]设(a,n)=1,那么 aø(n)≡1(modn),其中ø(n)表示1,2,…,n中与n互素的整数个数.

表2 RSA密码协议
例8假定Bob选取p=101,q=113,从而n=101×113=11413,ø(n)=100×112=11200,假定 Bob选取加密指数b=3533,那么解密指数a=b-1mod11200=6597.Bob在目录中发布n=11413和b=3533.现在,假设Alice想加密明文9726,她计算97263533mod11413=5761,然后将密文5761发送给Bob.当Bob收到密文5761,他通过计算57616597mod 11413=9726即可恢复明文9726.
4 结束语
《初等数论》课程的内容丰富多彩,它的基础知识可能并不难学,其难点是如何利用这些知识解决一些实际问题.在实际的教学过程中,大学老师切勿照本宣科,纯粹地把概念和定理传递给学生,而是应在适当的章节引入适当的竞赛题,并教会学生如何应用数论知识去解决这些问题,一方面提高学生的解题能力和逻辑思维能力,另一方面促使学生特别是师范生以较高的观点去看待中小学数学知识,为今后更好地从事中小学的数学教学和竞赛辅导打下良好的基础.适时地将《初等数论》课程与密码学联系在一起,丰富教学内容,激发学生的学习兴趣,培养学生从事科学研究的良好习惯,为今后毕业论文的撰写和进一步深造打下坚实基础.

