地铁列车动载作用下盾构隧道底部溶洞对管片动力性能的影响*

史海欧 翟利华 陈晓丹 陈俊生 高锐斌

( 1.广州地铁设计研究院有限公司，510010，广州; 2.华南理工大学土木与交通学院，510640，广州；3.华南理工大学亚热带建筑科学国家重点实验室，510640，广州//第一作者，教授级高级工程师)

0 引 言

我国岩溶地质分布广泛，许多已建乃至待建的盾构隧道项目都无法避开岩溶发育区。以广州市地铁线路为例，其拟建线路上普遍存在大量的岩溶地质。其中,地铁9号线全线溶洞见洞率约50%，部分工点甚至高达70%。

文献[2]以广州北站—花城路站区间为例，通过FLAC 3D软件研究了盾构穿越岩溶填充区施工过程中管片和围岩的变形；文献[3]采用MIDAS-GTS软件研究了广州地铁岩溶区盾构隧道周边不同形态的溶洞对隧道施工安全性的影响；文献[4]以深圳轨道交通3号线区间为工程背景，利用MIDAS-GTS软件研究了地铁盾构施工过程中围岩稳定性受周边溶洞方位和大小影响的变化规律；文献[5]以长沙轨道交通2号线为依托，结合FLAC 3D有限差分软件对盾构隧道穿越岩溶填充区进行了分析，结果表明，盾构隧道周边隐伏溶土洞极大地削弱了衬砌对地层的约束作用，且在其影响下，围岩和隧道结构的变形和应力水平显著增大。然而，上述研究讨论的主要是岩溶对隧道施工稳定性的影响，而针对隐伏型岩溶盾构隧道在运营期的动力响应及寿命评估的研究则相对缺乏。根据广州地铁9号线最新岩溶土洞的处理原则[6]，在地铁隧道施工前，仅对隧道一定范围内的溶洞进行处理，对于施工影响范围以外的溶洞，则采用双液浆封边后不再进行处理。考虑到该处理范围仅仅基于施工阶段的安全考虑，未作处理的溶洞在地铁长期振动荷载作用下仍有可能会影响到盾构隧道管片的疲劳寿命，一旦盾构隧道管片受未处理溶洞的影响而提前在地铁运营设计期限内产生疲劳破坏，势必造成隧道失圆，严重威胁盾构隧道的运营安全。

本文以广州地铁9号线复杂的岩溶地质条件为例，采用数值模拟手段，制定了盾构隧道底部存在溶洞时的数值试验方案。当盾构隧道底部隐伏溶洞大小及溶洞顶板厚度等因素变化时，对盾构管片在运营期地铁列车动载作用下的动力响应进行了分析，并结合经验公式对管片结构的疲劳寿命进行了研究。其研究思路与方法可对岩溶地区盾构隧道周边溶洞的处理提供参考和借鉴。

1 数值计算方法

1.1 动力理论及列车荷载

借鉴车路体系振动方程建立了盾构隧道-地层振动体系模型。该模型分别将地铁列车及隧道地层系统视为两个子系统，并通过轮轨间的几何相容及力学平衡条件来实现车隧之间的耦合效应，然后将由此得到的运行列车轮轨作用力以外荷载的形式输入到盾构隧道-地层动力子系统中，从而进行振动响应分析。

根据文献 [7-9]中已有的试验数据和研究成果得到荷载模拟方法，该方法通过采用一个激振力函数来模拟列车产生的动荷载F(t)。

(1)

式中：

k1——考虑线路方向上多组车轮之间的叠加系数[10-11]，通常取1.2～1.7；

k2——轨枕对单个轮载力的分散系数[10-11]，通常取0.6～0.9；

P0——车轮的静重；

Pi——分别为与轨道几何不平顺性相关的振动荷载[12]，i=1,2,3；

M0——地铁列车的轮下质量；

ωi——地铁列车振动的圆频率，i=1,2,3；

v——地铁列车的行驶速度；

ai——不平顺控制条件下的几何不平顺矢高，i=1,2,3；

Li——几何不平顺曲线的波长，i=1,2,3；

t——时间。

其中，ai与Li的取值如表1所示。

表1 英国铁路中心轨道几何不平顺控制值

本文k1取1.5，k2取0.8，P0取8.0×103kg[13]，M0取750 kg，v取108 km/h。L1取10 m时，a1取3.5 mm；L2取2 m时，a2取0.4 mm；L3取0.5 m时，a3取0.08 mm。地铁列车长度取132.6 m[14]，因此列车荷载作用时间为4.42 s。列车振动荷载如图1所示。

图1 列车振动荷载

1.2 动力模型

选取广州地铁9号线某典型岩溶区间盾构隧道断面建立动力分析模型。各岩土层及隧道结构力学参数如表2所示。

为了消除应力波在截断边界上的反射，本文参考文献[15]，计算时采用粘弹性动力边界模拟边界上的应力条件，即分别在边界的法线方向和切线方向设置弹性弹簧和粘性阻尼器来传递和吸收边界处的应力波，具体计算可采用弹簧-阻尼单元来模拟。法向边界及切向边界的阻尼系数和弹簧刚度为：

(2)

(3)

式中：

KBN，KBT——分别为弹簧法向刚度和切向刚度；

αN——法向粘弹性边界系数，取0.8～1.2；

αT——切向粘弹性边界系数，取0.35～0.65；

CBN,CBT——分别为法向阻尼系数和切向阻尼系数；

cP，cT——分别为介质纵波波速和横波波速；

G——介质剪切模量；

R——振动波源至人工边界处的距离；

ρ——介质质量密度。

表2 广州地铁9号线某典型岩溶区间各岩土层及隧道结构力学参数表

弹簧-阻尼单元如图2所示。其中，C表示阻尼器单元，K表示弹簧单元，i、j分别代表单元的两个节点。

图2 两节点的弹簧-阻尼单元

动力有限元模型的离散参数需要根据相应地层的剪切波波速及激励的频率范围来确定[16]。为了简化模型，同时又能反映地层的动力特性，根据地层剪切波速的变化范围，将复杂的真实地层简化为5层水平构造，每层代表一个主要的剪切波速域[17]。剪切波速cs的计算公式[18]为：

(4)

式中：

E——弹性模量；

υ——泊松比。

动力分析中，模型的截断边界距离振源应不小于介质的最大半波长。

(5)

式中:

L——模型截断边界离振源的距离;

λjd——介质的最大半波长;

fmin——最小振动频率。

文献[19]显示，当模型的水平范围为8～10倍隧道直径时，即可获得较高的计算精度。本文建立了二维弹塑性动力有限元模型，模型水平方向为80 m，竖直方向为60 m，盾构隧道直径为6 m。

为获得较高的精度，网格划分时单元尺寸Δl不应大于相应土层最小波长的1/6[20]，即：

(6)

式中:

fmax——最大振动频率。

为了简化计算，振源附近以及所关心的识振点范围内的网格，按照式(6)对单元尺寸的要求，取0.5 m；远离振源的单元逐渐放宽单元尺寸要求，本文取1 m。

本文建立的二维精细化盾构隧道-地层模型中，地层、管片和道床采用平面应变单元模拟，管片接缝、管片与地层间的注浆层以及管片与道床间的接缝均采用interface界面单元模拟，其物理力学参数[21]如表3所示。盾构隧道底部存在溶洞的有限元模型如图3所示。

表3 盾构管片各接缝物理力学参数

图3 广州地铁9号线某典型岩溶区间隧道-

为了真实反映隧道-地层模型体系在振动中能量的耗散，在动力时程分析时必须考虑阻尼的影响。本文采用Rayleigh阻尼[22-23]。为了保证足够的精度，MIDAS/NX软件程序规定，隐式积分的时间步长还应满足不大于所考虑的最高阵型周期的1/10[24]，并且分析的时间间隔不能大于输入荷载的时间间隔，本文采用的积分步长Δt=0.01。

1.3 数值试验方案

结合广州地铁9号线最新岩溶土洞的处理原则[6]，考虑施工期已对隧道结构轮廓外放1 m，以及对隧道底板以下2 m范围内的全部岩溶土洞进行处理，溶洞顶板的最小厚度取2 m。

实际工程中，溶洞的形态千差万别，在进行动力学分析时，不可能将其逐一讨论。本文参考文献[25-27]，假定溶洞断面形状为圆形，并将与盾构隧道轴线近似平行的溶洞、隧道和地层简化为平面应变问题来进行分析。详细方案如表4所示。

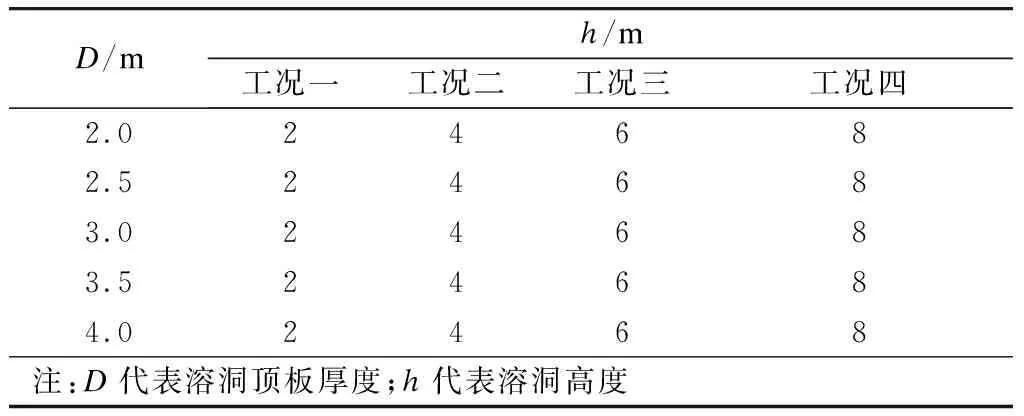
表4 广州地铁9号线典型岩溶区数值模拟试验方案

1.4 管片疲劳计算方法

盾构隧道在运营期能否满足设计使用年限，主要取决于列车在动载作用下盾构隧道管片承受疲劳荷载作用的次数。隧道周边存在溶洞，在一定程度上影响着管片的拉、压应力水平。依据混凝土疲劳寿命的相关理论[28]可知，混凝土管片的拉、压应力水平的变化亦影响着其自身的疲劳寿命。

隧道管片的受力比较接近于单向受力状态，管片的疲劳寿命是由其拉、压状态共同决定的。因此，采用单轴受拉疲劳经验公式(7)[29]来对管片进行受力计算，采用单轴受压疲劳经验公式(8)[30]对管片的疲劳寿命进行验算，其计算公式如下：

logNf=11.24-14.52Smax+2.79Smin

(7)

(8)

式中:

Nf——管片的极限受拉或受压疲劳次数;

Smax——管片的最大拉、压应力水平;

Smin——管片的最小拉、压应力水平。

式(7)～(8)中，管片的应力水平是其拉、压应力分别与混凝土材料的轴心抗拉、抗压强度的比值。管片混凝土的材料参数选取其强度标准值作为应力水平的计算依据。管片混凝土材料的计算参数如表5所示。

表5 管片混凝土材料的计算参数

2 管片应力响应分析

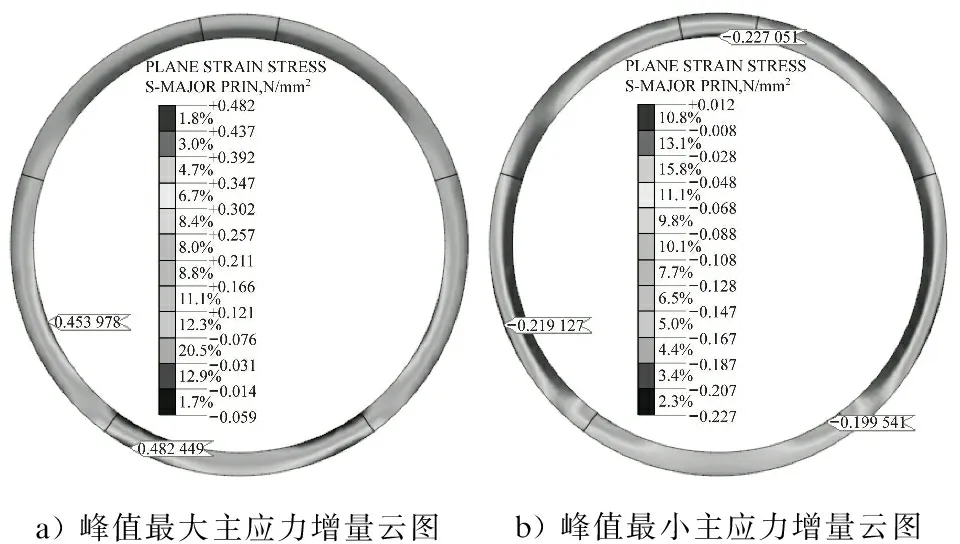
图4～5为自重应力作用下隧道管片主应力云图。图6～7为列车动载作用下隧道管片峰值主应力增量云图。由图4～7可知：

a) 最大主应力云图b) 最小主应力云图

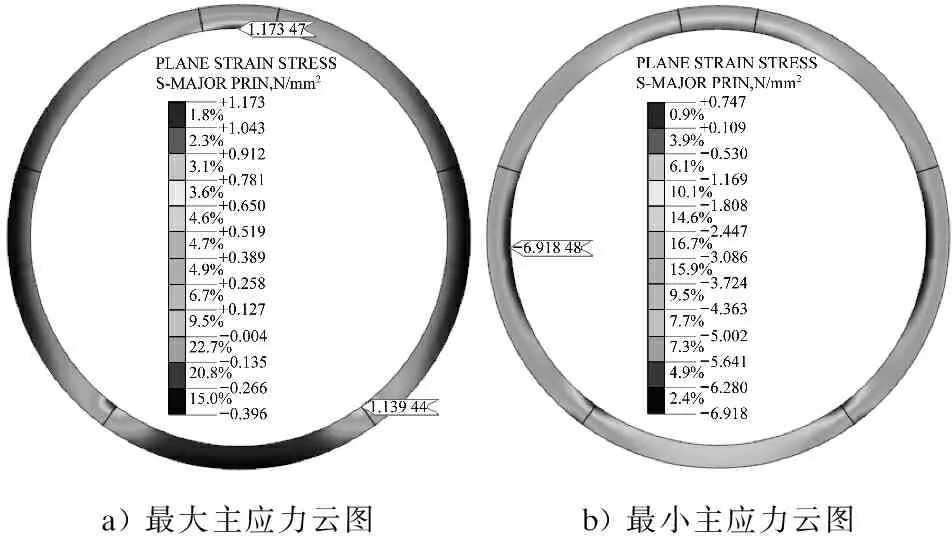
图4 隧道底部无溶洞时管片在自重

图5D=2 m，h=8 m时管片在自重应力作用下的主应力云图

(1)无论溶洞存在与否，管片在自重应力作用下的应力分布以及管片在列车动载作用下的应力增量分布都无明显变化。但溶洞存在时，管片的应力响应会有所增加。

(2)在列车动载作用下，管片会产生一定的拉应力和压应力增量。其中，最大拉应力增量集中在管片标准块拱腰中部内侧和拱底块端部外侧，这些位置在自重应力作用下表现为压应力；最大压应力增量集中在管片标准块拱腰中部外侧、拱底块端部内侧及拱顶封顶块内侧，这些位置在自重应力作用下表现为拉应力。因此，在列车动载作用下，隧道管片断面的拉应力和压应力水平均存在一定程度的降低。

a) 峰值最大主应力增量云图b) 峰值最小主应力增量云图

图6 盾构隧道底部无溶洞时管片在动载作用下的峰值主应力增量云图

a) 峰值最大主应力增量云图b) 峰值最小主应力增量云图

图7D=2 m，h=8 m时管片在列车动载作用下的峰值主应力增量云图

3 管片疲劳寿命预测分析

通过前文对管片的应力响应分析可知，由静力计算可得到管片的最大应力水平，由动力计算可得到管片的最小应力水平。通过式(8)和式(9)可计算出管片的极限拉、压疲劳次数。管片的疲劳寿命计算流程如图8所示。

图8 管片的疲劳寿命计算流程图

以盾构隧道底部无溶洞的情况为例，通过计算可得到管片的极限受拉疲劳次数为1.358×107次，极限受压疲劳次数为3.147×1014次，两者之间相差7个数量级，说明管片的疲劳寿命是由极限受拉疲劳次数决定的。

广州地铁平均每天运营时间为17 h，取相邻两列车平均运行时间间隔为3 min，则每天地铁列车动载作用于管片的次数为340次，每年作用于管片的次数为124 100次。通过上文求得的管片极限受拉疲劳次数除以124 100即可得到管片的疲劳寿命。图9为管片受拉疲劳寿命变化曲线。

图9 管片受拉疲劳寿命变化曲线

由图7可知，在列车动载作用下，管片的疲劳寿命随着盾构隧道底部溶洞高度的增加以及溶洞顶板厚度的减小而降低。通过管片受拉疲劳寿命变化曲线可查得，管片疲劳寿命不满足盾构隧道管片100年运营设计使用年限时溶洞高度与溶洞顶板厚度的组合情况。对于管片疲劳寿命不满足设计使用年限的情况，宜采取适当的措施对溶洞进行处理或对管片进行优化设计。

4 结 论

通过以上盾构隧道管片应力响应及疲劳寿命分析，得出以下结论：

(1)盾构隧道底部溶洞的存在基本不改变管片的拉、压应力分布状态，但应力水平有所增加。

(2)管片的疲劳寿命计算结果显示，管片的疲劳寿命由极限受拉疲劳次数决定。

(3)在地铁列车动载作用下，管片的疲劳寿命随底部溶洞高度的增加或溶洞顶板厚度的减小而降低。