中低速磁浮列车转向架固有特性分析*

夏文韬 王 珍 张志新

(大连大学机械工程学院，116622,大连//第一作者，硕士研究生)

转向架作为磁浮列车的主要受力部件，其动态特性优劣对列车的安全稳定运行影响重大[1]。中低速磁浮列车在唐山试验运行过程中，曾出现列车振动的现象，影响乘车人员的舒适性和安全性。这种振动是由于轨道梁的收缩和徐变以及车辆等负载加载后引起静扰度导致轨道梁不平顺而引起的。列车振动频率与梁跨度和列车速度有关，频率为0～5.8 Hz[2-4]。因轨道不平顺的存在，转向架在运行过程中不但存在左右模块同向和反向的浮沉、俯仰、侧滚运动，同时还存在弹性模态的振动，即结构的弹性振动。当外界激励的频率成分与弹性模态频率相近时，会产生共振。目前，在转向架动态特性分析中，大多将转向架视为刚体，并研究其运动状态。结构内的弹性振动响应一般肉眼难以察觉。结构的内部振动变形是由各阶弹性模态对激励响应的叠加而得到的。当结构振动变形时，转向架受力会发生变化[5]。尤其是当电磁铁梁振动时，悬浮力会出现振荡。当激励频率与转向架固有频率错开时，就不会产生共振。因此,需对转向架的弹性模态参数进行分析，并验证其准确性。其研究结论可为结构优化和悬浮控制参数[6]的改进提供参考。

1 列车振动原因分析

轨道不平顺的空间频率[4]范围为0.055～0.174 m-1时的功率谱密度值较高。中低速磁浮列车一般运行车速为0～120 km/h，对应时间频率范围为0～5.8 Hz。轨道的不平顺会引起悬浮间隙的变化，悬浮间隙的变化会引起电流的变化，电流变化会引起悬浮力的变化。中低速磁浮列车的垂向悬浮力如图1所示。由图1分析得到，小于6 Hz的低频周期脉冲冲击幅值较大，且与轨道不平顺的时间频谱相吻合。

对于磁浮列车振动问题，有研究将转向架等效成质量块,将悬浮力类比成弹簧力，悬浮力在平衡位置处有近似值恒定的刚度值和阻尼值[8]。这种等效方法未考虑到电磁铁梁的弹性振动，当电磁铁梁发生弯曲振动时，会导致悬浮力出现非均匀分布(见图2)。图2中,相对于平衡位置，电磁铁梁两头因间隙减小导致电磁力增大，因中间间隙增大导致电磁力减小，总体上叠加的电磁力呈减小趋势。但电磁铁梁两端涡流间隙传感器反馈的间隙是减小的，这时通过PID(比例-积分-微分)反馈调节会使悬浮力更小，这样使得电磁铁梁总体位置低于平衡位置;但当弯曲振动相位发生180°变化时的情况正好相反。所以电磁铁梁的振动会引起悬浮力振动，从而加剧轨道、转向架及悬浮控制的振动耦合，甚至产生振动发散现象。为避免上述现象的产生,一方面,可以增加间隙传感器的个数，并根据轨道不平顺引起的电磁铁梁的振动变形来改进与增强悬浮控制算法。但由于该振动是由轨道自振、转向架振动及电磁力振荡相互耦合的，需要较为复杂的悬浮算法，因此必然会增加控制系统的风险。另一方面,可从机械结构进行分析和改进，通过分析转向架的固有特性，将转向架的固有频率与激振力的固有频率错开，避免产生共振现象。

图1 中低速磁浮列车的垂向悬浮力

图2 电磁铁梁弯曲振动时受力简图

2 转向架结构的固有特性仿真分析

2.1 模型建立

磁浮列车转向架分为左右两大模块,由主梁、防滚梁和电磁铁梁组成，各部分采用螺柱或焊接连接，有较多的孔和凸台，结构较为复杂。建立转向架模型时，可对其进行适当的简化，如对小孔结构填充、将螺柱连接近似为刚体连接、小凸台切除。转向架模型如图3所示。转向架结构主体采用铝合金。材料性能参数如表1所示。

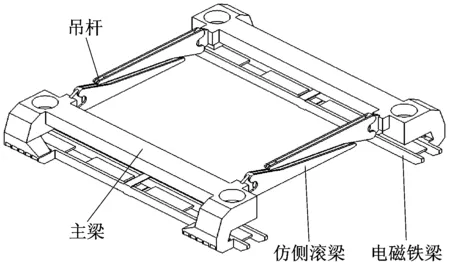
图3 磁浮列车转向架结构简图

名称密度/(kg/m3)泊松比弹性模量/GPa屈服极限/MPa铝合金2 7700.3371280

2.2 仿真模态分析

将在Solidwork模块中建立的转向架模型导入ANSYS中，模型采用六面体单元，共划分了27 894个单元体，节点总数为13 430个。转向架处于悬浮状态时，电磁铁梁受电磁悬浮力支撑，不与轨道接触，电磁约束对刚体模态影响较大，但对弹性模态影响可忽略。对其进行弹性模态分析时，将边界设置为自由边界，提取前6阶弹性模态频率,如表2所示。磁浮列车转向架前6阶模态振型如图4所示。由图4可知，转向架模态振型比较复杂，其振型是多个部件的组合变形，虽能从振型图中观察分析到模型的整体振型，但对某个部件或方向的振型分析比较困难，而磁浮轨道的不平顺主要是垂直方向的不平顺，激励方向主要集中在垂直方向，同样转向架悬浮控制对垂直方向的振动亦比较敏感。所以需要将其模态参数特征降维，通过试验测试方法将模态频率振型分解映射到单方向来进行分析。

表2 磁浮列车转向架前6阶频率统计表

b) 2阶模态

d) 4阶模态

e) 5阶模态

f) 6阶模态

3 固有特性试验测试分析

3.1 试验测试

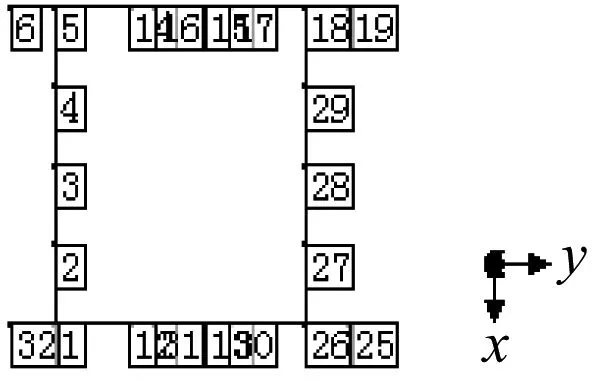
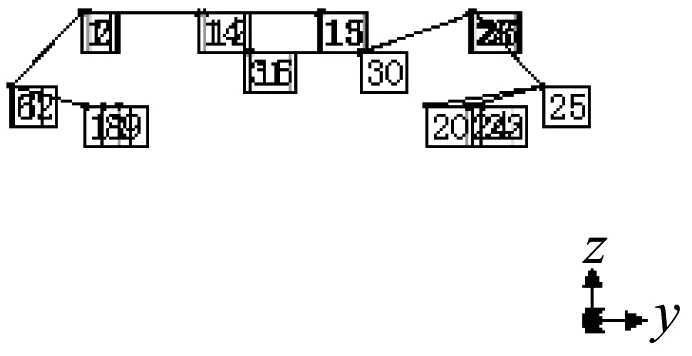
采用锤击法对转向架进行模态测试试验。首先将在转向架上需要安装压电加速度计的点进行标记和处理，骨架模型上的每个点即为测点。转向架骨架模型如图5所示。图5中,X方向与轨道纵向一致，Y方向与轨道横向一致，Z方向为垂直方向。

图5 磁浮列车转向架骨架模型

测点标记完后，用悬浮控制装置驱动电磁铁线圈，产生的磁力可平衡重力和惯性力，使转向架悬浮在试验轨道上，并使其与轨道的悬浮间隙控制在8 mm。试验测试时，分别对转向架单方向的模态进行测试。首先，用力锤沿Z方向锤击驱动测点28，并采集响应点Z方向的振动信号，可得到响应点对驱动测点的频响函数，依次测量转向架上所有测点对驱动测点Z方向的频响函数。然后用力锤沿Y方向锤击驱动测点28，并采集响应点Y方向的振动信号，得到转向架上所有测点对驱动测点Y方向的频响函数。最后,用力锤沿X方向锤击驱动测点28，并采集响应点X方向的振动信号，得到转向架上所有测点对测点X方向的频响函数。为了使数据具有可靠性，每移动一次压电加速度计，应锤击多次，并检查频响函数的相干性，剔除不良数据。

3.2 模态参数的提取

模态参数提取时,首先要对频响函数进行曲线拟合。曲线拟合常用正交多项式法和LCSE最小二乘复指数法。频响函数[9]中包含了模态参数，其表达式为:

(1)

式中：

Hlp(s)——具有N阶自由度的时不变系统中的l、p两点间的频响函数；

Alp,r——Hlp(s)的第r阶模态的留数；

sr——第r阶模态的极点值，包含模态频率和阻尼信息；

其中,sr为:

(2)

式中：

ωr——系统第r阶无阻尼模态频率；

ξr——系统第r阶模态的阻尼比。

采用正交多项式分别对频响函数的分子、分母进行拟合，得到分子、分母系数后，令分母多项式为0，可求得极点s。在已知极点s的情况下,对式(1)两边同乘以(s-sr),可求解留数Alp,r。当l=1，2，…，N时，重复以上计算，可得Ar。将Ar进行归一化，便可得振型系数列阵φr[11]。

φr=Ar

(3)

对各测试点的频响函数进行拟合，通过式(1)、(2)、(3)便可得到各阶模态频率和模态振型。

3.3 试验结果分析

表3、4、5分别为Z、Y、X方向的前3阶模态频率和阻尼统计表，图6、7、8分别为Z、Y、X方向的1阶模态振型。因为模态振型具有较强的方向性，单方向的模态频率、振型与仿真整体模态频率、振型的阶数并不一定相等。

从Z方向进行分析，表2和表3中的1阶固有频率对应仿真中的整体第1阶固有频率。Z方向的1阶模态振型如图6所示。该振型为电磁铁梁Z方向的弯曲变形，电磁铁梁在Z方向相当于一个大跨度简支梁，其在Z方向的刚度比较小，所以1阶频率较低。Z方向的2阶固有频率对应仿真中的整体第3阶固有频率，Z方向的3阶固有频率对应仿真中的整体第4阶固有频率。其中,Z方向的1阶和3阶固有频率数值与对应的仿真固有频率数值吻合较好，误差较小。

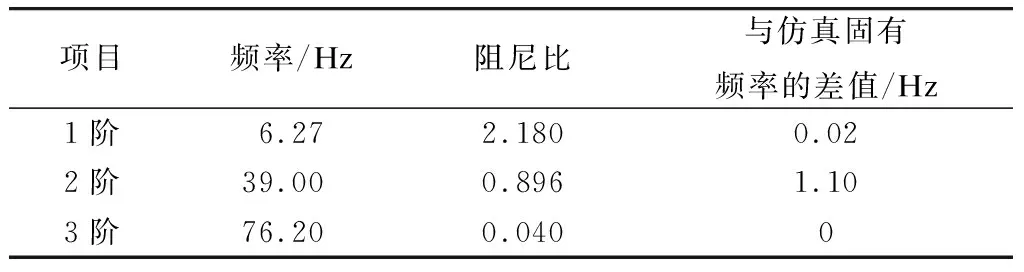
表3 Z方向前3阶固有频率和阻尼比统计表

从Y方向进行分析，表2和表4中的1阶固有频率对应仿真中的整体第3阶固有频率。由图7可知,Y方向的1阶模态振型主要是电磁铁梁沿Y方向产生的弯曲变形。电磁铁梁在Y方向因有电磁铁固定板而增加了Y方向的刚度，所以其Y方向的1阶模态频率比X方向的1阶模态频率高，当轨道出现Y方向的不平顺时，一般不会产生共振。Y方向的2阶固有频率对应仿真中的整体第4阶固有频率，Y方向的3阶固有频率对应仿真中的整体第5阶固有频率。其中，Y方向的2阶和3阶固有频率数值与对应仿真中的固有频率数值吻合较好。

表4 Y方向前3阶固有频率和阻尼比统计表

从X方向进行分析，表2和表5中X方向的1阶固有频率对应仿真中的整体第1阶固有频率。由图8可知,X方向的1阶模态振型主要是防侧滚梁沿X方向的弯曲变形。左右模块的防侧滚梁通过可活动的吊杆连接，该连接属半柔性连接，且为左右模块的悬浮控制提供解耦，而当防侧滚梁出现振动时,左右两模块易出现振动耦合，从而影响两模块的控制解耦性。X方向的第2阶固有频率对应仿真中的整体第2阶固有频率，X方向的第3阶固有频率对应仿真中的整体第5阶固有频率。其中1阶固有频率和3阶固有频率与对应的仿真固有频率吻合较好。

表5 X方向前3阶固有频率和阻尼比统计表

4 转向架结构改进及改进后的转向架实测振动信号分析

原转向架电磁铁梁和防侧滚梁壁厚分别为25 mm、12 mm。为提高1阶固有频率，增加电磁铁梁及防侧滚梁的壁厚至30 mm、15 mm。通过测试得到改进的转向架结构Z方向的1阶固有频率为8.3 Hz，比原转向架提高了32.4%。对改进后中低速磁浮列车转向架的振动信号进行实测分析。在主梁中间位置，即点28处垂直安装压电加速度计,转向架通电后处于悬浮状态，同时转向架以80 km/h的速度沿着试验轨道运行一小段时间，此时采集测点的振动加速度。图9为截取1 s的振动加速度信号。

对测点振动加速响应信号进行时域统计，统计出均方根值、峰值、峰-峰值，如表6所示。

对转向架振动信号进行谱分析，其加速度功率谱密度曲线如图10所示。该响应点的功率谱密度曲线在8 Hz、28 Hz、40 Hz、77 Hz、86 Hz、130 Hz处出现了极值点，由于测量精度和分辨率不够，极值点的频率与模态固有频率存在一定的误差。转向架在运行过程中，悬浮力不仅含有因轨道不平顺引起的低频成分，还有因悬浮控制引起的白噪声激励成分。极值点是转向架各阶固有频率对悬浮力的响应，由于各极值点幅值较小，所以转向架未发生强共振，转向架结构固有频率避开了轨道不平顺频谱段。根据图10可得出其幅值均小于0.001 64(m·s-2)2/Hz,符合GB/T 21563—2008/LEC 61373《轨道交通机车车辆设备冲击和振动试验》的要求。

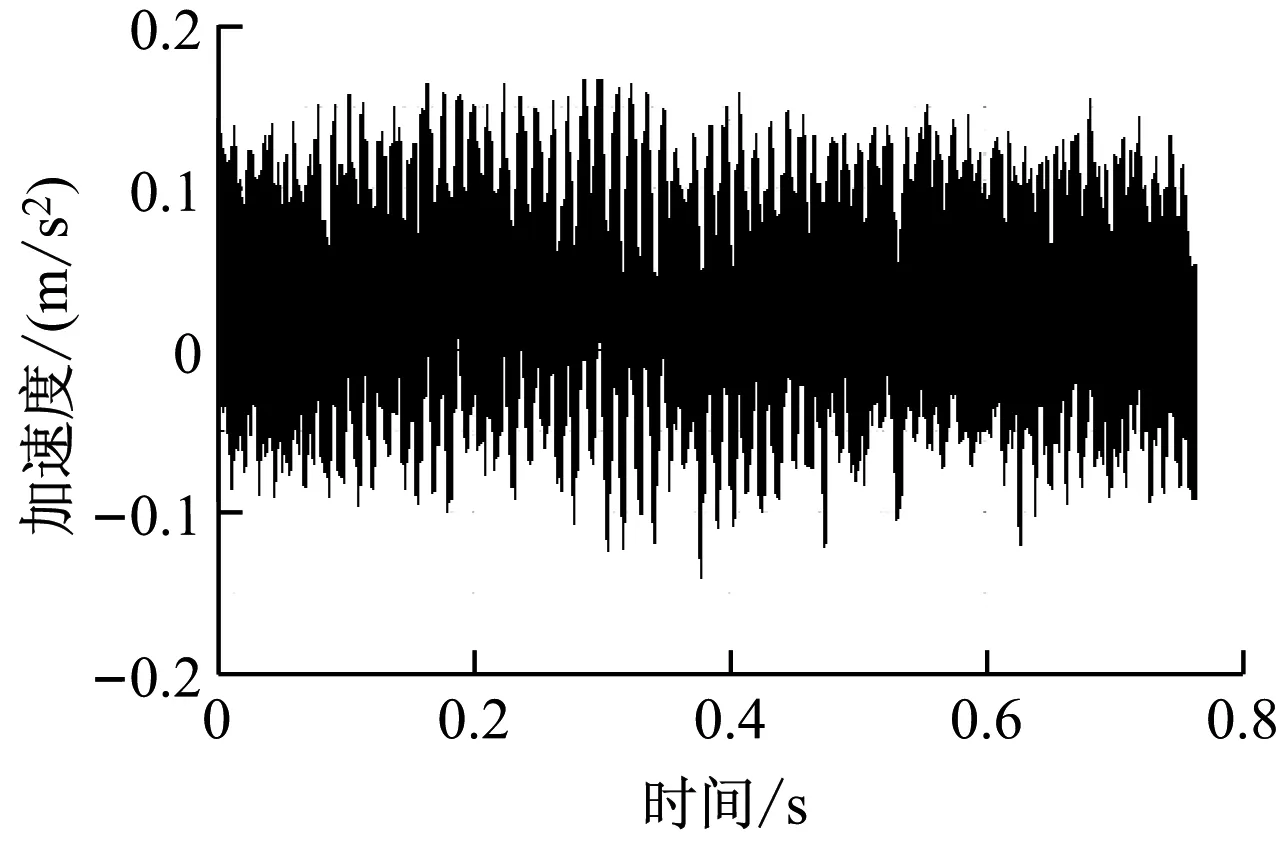
注：采样频率为10 kHz

图9 测点振动加速度信号响应

图10 转向架振动响应点的加速度功率谱密度曲线

5 结论

(1) 提出了转向架结构弹性振动是导致轨道悬浮不平顺的一个重要原因,因此需分析转向架结构的固有特性，来解决列车振动问题。

(2) 仿真计算得到了中低速磁浮列车单转向架的前6阶模态固有频率值。根据测试点建立了磁浮列车转向架骨架模型，通过锤击模态试验获得了一系列频响函数，分析和处理试验数据得出了X、Y、Z方向的前3阶试验模态频率、阻尼和振型。转向架振动时，1阶模态振型占主导，X方向主要为防侧滚梁的弯曲，Y、Z方向主要为电磁铁梁的弯曲;当共振发生时，电磁铁梁弯曲振动变形会导致电磁力大小发生变化，进而加剧振动。悬浮振动和轨道不平顺振动频率最大为5.8 Hz，转向架1阶固有频率为6.23 Hz,当两频率相近会产生共振。为防止电磁铁梁和防滚侧梁由于悬浮振动和轨道不平顺而产生共振，应提高电磁铁梁和防侧滚梁的结构刚度。

(3) 试验与仿真结果相近，验证了结果的可靠性。对比了仿真与试验测试模态之间误差，该误差来源于仿真和试验两个方面：仿真时对模型进行了简化，而试验测试时转向架振动信号存在系统误差和噪声干扰等问题。

(4) 改进后的中低速磁浮列车转向架振动的加速度功率谱密度表明,转向架结构固有频率避开了轨道不平顺谱频段，改善了转向架运行状态，其加速度功率谱密度符合轨道交通相关振动标准的要求。