多元表征完善计算学习的内在结构——以《20以内退位减法》单元教学为例

钟 燕

计算学习是数学学习中学生较早接触的内容，在小学数学课程中占的比重比较大。20以内加减法作为整个计算学习的基础，有着举足轻重的地位。其中20以内的退位减法，是学生在学习过程中遇到的一个难点。如何借助多元表征，帮助学生在理解算理的基础上掌握算法，同时形成有利于后续计算学习的结构特征？我们以整个单元教学为研究内容做了一些新的尝试。

一、合理运用表征，突出“退一当十”的位值概念

我们现在使用的是十进制的计数制，在一年级上学期学生学习了20以内数的认识，知道了一个十等于十个一；学习了20以内的进位加法，对“满十进一”有一定的了解，而20以内退位减法的关键就是理解“退一当十”。

1.提供有结构的材料，迁移同类算理。

基于学生的认知水平，北师大版教材中呈现了很多实物图帮助学生理解退位减法。但是教材的图中，“十”的计数单位不清晰。课堂中我们提供了以10为单位的有结构的材料，如下图：

有结构的图和没有结构的图对于学生学习退位减法的效果是不一样的。没有结构的材料只是让学生根据减法运算的意义求得算式的值，而有结构的材料有助于学生理解退位减法的算理，并且以10为单位的结构有助于后续同类算理的迁移。

2.找准表征的切入点，便于学生运用。

各种表征都需要学生尝试表达，学会运用。对于一年级的学生来说，认识一种新的表征或数学模型需要一个过程。在退位减法单元教学的新授课中，我们以被减数不变，减数变化展开教学。如12-3，12-4，12-5，在表征时都是先表示出12，这样学生更容易找到表达的起点，并摸索到路径先做什么，再做什么。被减数不变，不管是语言表征，还是图形表征、操作表征等，在表征的初始阶段都是一样的。学生熟悉表达以后，方便运用和重复。另外，被减数不变，减数变化，更易于引起学生关注运算的发生。

二、逐级抽象表征，重视刻画算理

在计算学习中，课堂上要完成习题，教师往往更在意学生计算的结果的正确。《数学课程标准（2011版）》把“运算能力”列入十大核心概念，强调了运算能力的重要性。所以初始阶段，我们也需要重视学生对于运算算理的理解，发展学生的计算思维，从而为后续的计算学习打下扎实的基础。

1.强化重点内容。

现行教材更强调算用结合，算用结合的推行也确实有着非常积极的意义，但同时也发现课时容量往往偏大。如北师大版一年级下册第一单元《20以内退位减法》的第一课时“买铅笔”。

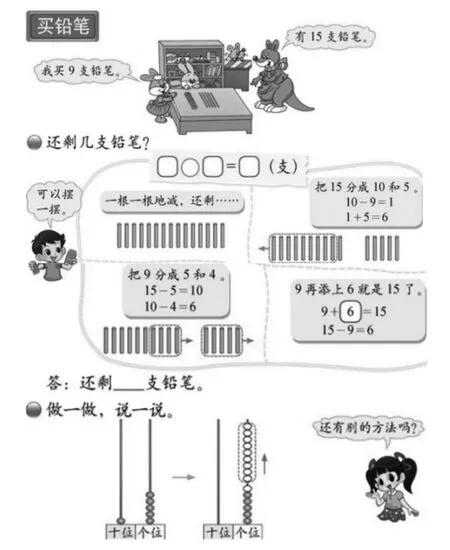
这节课常用的流程是先呈现问题情境，学生解读数学信息并提出数学问题，根据数学问题列出算式15－9＝；再讨论交流15－9的多种算法；然后借助摆小棒、拨计数器等操作模型理解算理。这样一个过程下来，只一道题预计教学时间就会超过20分钟。在前一个环节没有理解巩固的情况下，匆忙进入下一个环节，计算教学容易存在蜻蜓点水走过场的现象。一年级学生本身注意力相对不集中，注意持续时间也相对较短。根据这些现状，在《20以内退位减法》的单元教学中，教师更需要每节课在最佳时间段强化重点学习内容。基于这样的考虑，将单元新授内容重新进行了厘定，如下表：

?

以上每课时的重点内容集中在前20分钟教学，后20分钟进行相应的练习。如此便可以让计算方法交流更充分，学生对于表征的理解更扎实。

2.同种表征适度反复。

在一个课时中，教师常会运用两种或两种以上表征来突显算理。但是因为表征多样以后，受时间和学生接受程度的限制，每一种表征在运用的时候，学生经常性地处于一种模仿的阶段，而缺少内化的过程。这样不利于学生充分掌握表征的运用方法，从而深入理解退位减法的算理。我们在设计单元教学的前面几节课时，每节课都只侧重一种表征方式。教学环节中有相似的流程，每一种方式的学习都主要经历了以下几个阶段：

如下，为计数器模型的教学片断：

师：我们在计算12－3的时候怎么想？先怎么做，再怎么做？

生：先把12拿开，从10里拿出1个。

师：拿出1个之前先怎么样？

生：先从12里减去2，因为要减去3，所以再从10里减去1，结果等于9。

师：非常棒，因为12的个位上是2，所以把3分成2和1，12先减去2等于10，10减1等于9。像这个过程，昨天我们是画图表示的。今天如果是用计数器拨出来的话，大家想先怎么样？再怎么样？

生：12的个位上先减2，十位上还剩1个珠子。

师：这十位上的珠子怎么办？

生：十位上的1个珠子，相当于个位上的10个珠子。

要求：大家自己拨一拨，再同桌一起拨一拨。请一位学生上讲台边讲边拨。

（教师根据学生拨的过程，在图中示范画。之后请学生在练习纸上把拨的过程画一画，再反馈交流）

从上述片断中可以看到，12－3的“平十法”主要借助计数器模型，使得学生在同一水平层次上有一个反复的过程。适度反复能够让学生有重复表达的机会，从而使学生在脑中形成表象，实现面向全体学生的意义理解和思维深度。

3.逐级提高表征的抽象化水平。

在学习20以内退位减法中，运用的表征形式主要有动作表征（摆小棒、圈图形、拨计数器）、表象表征（回忆操作过程，用图式表示）、语义表征（说算理）、符号表征（用分解算式表示）等。从课时来看，每节课中都运用到动作表征、表象表征、语义表征、符号表征。使用顺序上不尽相同，也会有重复，但基本上遵循从简到难的过程。从单元序列来看，小棒、计数器和数线三种主要模型的运用依据由直观逐步走向抽象的顺序。结合使用，逐级提高，丰富并发展了学生对于算理的理解，同时也使得学生的思维更加的多元。

三、贯通多种表征，形成符合学生认知的网状结构

表征素材是决定学生数学学习活动质量、影响课堂学习效率的重要因素，也是贯穿学习活动的线索。但是表征本身作为一种意义理解的辅助形式，并不具备很大的学习意义。本单元贯通多种表征，形成相应的结构特征，使其具有更大的学习价值，并为后续同类知识的学习起强大的支撑作用。

1.思维在前，促进表征的结构化生成。

思维的产生不可能仅仅依赖于表征，所以在每一个具体的表征方式之前，都需要学生有独立的思考。如在单元第一课时探索12-3=9的算理环节：

思考：为什么12－3＝9是对的？是怎么解出来的？

提出操作要求：下面请同学们从学具袋中拿出12根小棒，看哪位同学最快。

师：想一想，12－9你是怎么做的？（先想不动）12根里拿掉3根，你准备怎么拿？

思考在前，学生可以产生各种不同的方法，不受制约。同时，思考后的动手表征可以促进学生对于方法的理解，固化思维方式。动作带动思维，可以让思维更深刻；思维引领操作，可以促进表征的结构化生成。

2.同一种思考方式，纵向联结多种表征。

每一种表征方式虽然有各自的外在表现形式和特点，但多种表征方式之间的内在并不是割裂的。就20以内退位减法而言，如13－5主要有三种思考方式：一是想加算减，想 5+（8）＝13，所以 13－5＝8；二是“平十法”，先把 5 分成 3 和 2，用 13－3＝10，10－2＝8，所以 13－5＝8；三是“破十法”，13 分成 10 和 3，10－5＝5，5+3＝8，所以 13－5＝8。想加算减，更多的依存加减运算的互逆关系。而后两种方式，每一种思考方式都在不同的课时中借助了不同的数学模型和表征方式。同一种方式的不同表征，抽象程度逐级提升，而表征之间其实又有紧密的联系。实现表征之间的内在沟通，可以促进学生认识计算方法的本质。所以在设计单元第五课时的时候，对前面几节课的学习内容进行了梳理，感受用图形、计数器、数线、算式都可以来解决退位减法，并能联系多种表征，沟通20以内退位减法的算理与算法。课堂伊始，抛出一个问题“想一想15－7怎么算，你有什么好办法？”唤醒学生前期积累的活动经验。教师引领学生在自我尝试、集体交流互动中，把多种表征融会贯通，并以直观、排版清晰的板书统领整节课。如下图：

纵向联结多种表征，可以为学生初步建立一个意义丰富的核心知识的认知单元，在这个认知单元的基础上，再学习其他的计算内容可以正向迁移，从而不必再进行认知的重构。对于学生的后续学习具有长期的意义。

计算教学中，多元表征能够帮助学生从具体到抽象地认识运算的本质。学生尝试表征，尝试分享自己的表征信息的同时，也促成了自我反思、自我调整，在互相学习、自我内化的过程中完善自己的内部表征，从而有效地把握计算学习的关系结构模式。多元表征所产生的形象直观的思维方式和简洁有效的思维结构，使得学生在学习新的同类型知识时，能够快速地激活原有的知识块，提高学习效率。