双连杆Acrobot机器臂的最优控制器设计

张志飞 ，章兢 ，曾凡智

（1.佛山科学技术学院自动化学院，广东佛山528000；2湖南大学电气与信息工程学院，湖南长沙4100823.佛山科学技术学院电子与信息工程学院，广东佛山528000）

Acrobot是一种在垂直平面上运动的欠驱动两连杆机器人[1]。这种机器人由于在肘部关节减少了驱动装置，使得系统在重量、成本及能耗等方面具有很大的优势；同时驱动装置的减少也使得机器人的动力学模型受到二阶的非完整条件约束，因此要对其进行控制设计具有很大的难度[2]。

近二十年来，为实现Acrobot在垂直向上平衡点处的稳定控制目标，学者们进行了深入研究，提出了多种控制方法。具有代表性的结果可概括为二类，一类是控制无约束条件下的连续控制律[3-5]，另一类是控制受限下性能指标最优控制律[6-8]。由于Acrobot非线性复杂，构造合适的Lyapunov去寻找合适的控制律没有明确的方法，需要很高的技巧。在控制受限条件下，可以利用极大值原理来求得控制律，但极大值原理所求控制律仅是性能指标最优的必要条件，并不能保证性能指标最优。关于性能指标最优控制，文献中常见的是时间最短MTC（minimum time control)作为性能指标[6-7]，针对其它形式的性能指标的控制律设计鲜有报道，也少见最优性能指标下的控制律的稳定性分析。

取时间与控制能量均衡最小为性能指标，讨论控制律的设计问题。考虑到起始区控制律仅能保证系统收敛至最大不变集，同时考虑在垂直平稳点附近连杆的姿态调整要求，将最优控制律切换至LQR，以确保运动过程平稳性。运用LaSalle′s不变集原理讨论了控制量有无约束二种情形下的最优控制律的系统稳定性，全局稳定性由切换定理保证。

1 Acrobot控制问题描述

Acrobot的模型结构如图1所示。其中mi（i=1，2），表示第i杆的质量，li是第i杆的长度，lci代表从i关节到i杆质心的距离，Ii表示为第i杆相对于质心的惯性，q1表示第一杆相对于垂直向上y轴的角度，q2表示第二杆相对第一杆的角度，τ2是作用在第二连杆上的控制力，g为重力加速度。

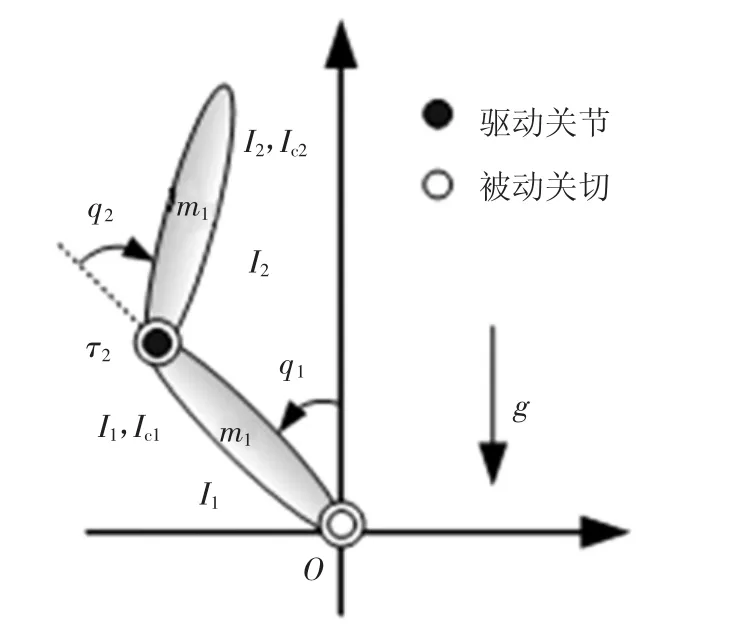
图1 Acrobot的模型结构

令 q=[q1，q2]T，Acrobot的动力学方程满足[1]

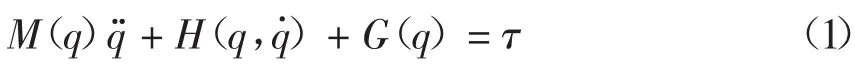
式（2）中，

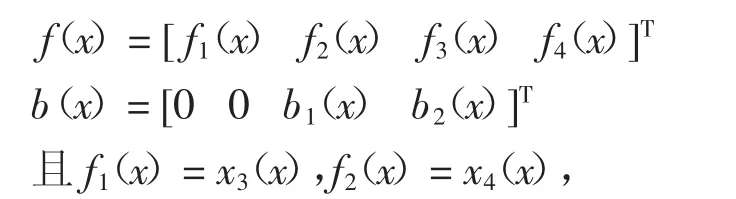
f3（x），f4（x），b1（x），b2（x）为非线性函数，它们分别为

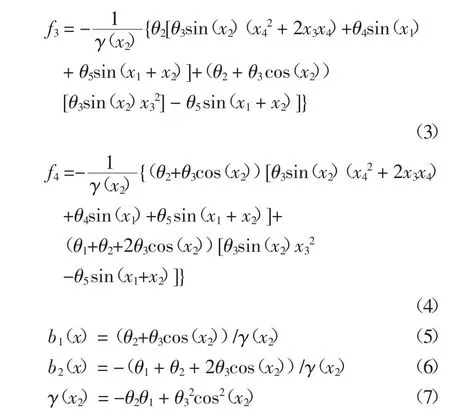
Acrobot的摇起控制目标为：从垂直向下的稳定平衡点 x0=[π，0，0，0]T摇起到垂直向上的不稳定平衡点 xd=[0，0，0，0]T。

2 控制器设计

为实现这一目标，本文采用最优控制的思想来设计来设计控制律。取性能指标为：

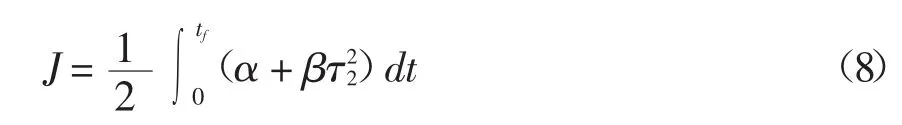
对应的Hamilton函数为

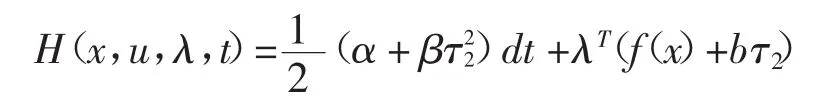
则J取极值的条件为[8]：

正则方程：

控制方程：

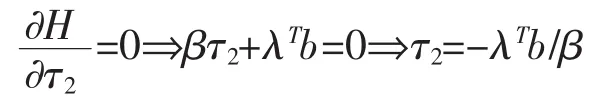
将τ2代入正则方程有

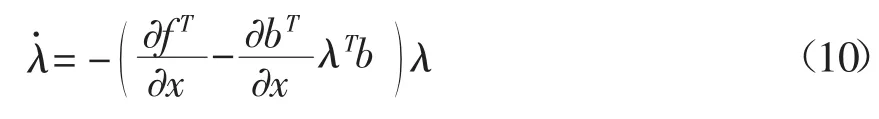
将上述讨论概括为下列定理：

定理1 设控制率无约束，则优化性能指标（8）的控制律为

其中参数λ满足式（9）。

从式（11）容易得到下列结论：

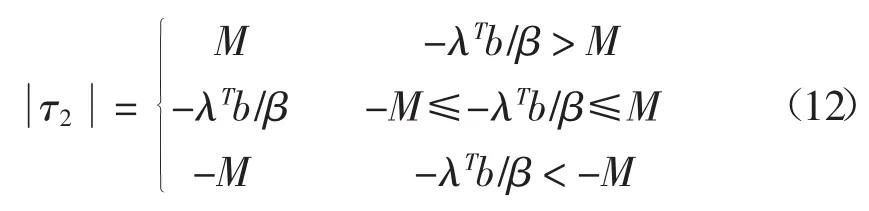
对于时间最短性能指标MTC，即性能指标为

在式（12）中取β→0+，便有下列结论:

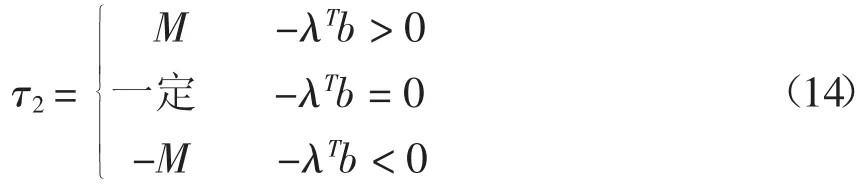
这是众所周知的bang-bang控制。

至此优化控制问题转化为解其初始条件为x（0）=[π000]T，λ（0）（为待定参数），求解微分方程组（2）和（10）的问题。

3 稳定性分析

系统在任一位置的能量

其中：

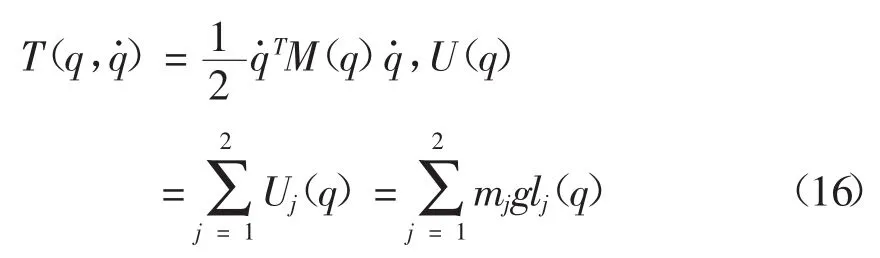
将上式改写为状态空间形式，有

计算E（x）关于时间的全导数，有

构造Lyapunov函数

Ex=E（x）-Ed，Ed为顶点处势能，δ为合适大小的正常数。

由式（18），沿运动轨迹（2）计算 V（x）的关于时间的全导数，利用式（18），有

取τ2=-Msign（Exx4），则有（x）≤0。换言之，存在bang-bang控制律，使V（x）单调不增。由拉萨尔不变集原理[9]可知，系统将收敛到不变集。

下面讨论连续控制律式（11）下的稳定特性。设有某bang-bang控制律τ2使系统收敛到不变集，即（x）=Exx4τ2≤ 0。由式（14）知，-λTb 与 τ2同号，故Exx4τ2≤ 0→λTbExx4≤ 0，此意味式（10）的控制律也能使系统收敛至不变集。

将上述结论概括如下：

定理3 最优化性能指标的控制律确保系统运动至系统的最大不变集。

许多文献的研究表明，一般情况下，系统的不变集包含了垂直顶部不稳定平衡点，但并不能保证系统运动至不稳点，系统将在不变集上做周期运动，这种情况下，须采取另一种控制律打破这种周期运动，这种切换控制的稳定性由开关定律得以保证。一种较为常见的处理方法是，在系统运动至不变集过程中，当系统的状态变量满足线性化条件时，将系统线性化，采用线性系统理论来设计控制器[3][5]。线性系统理论已经成熟，这里不做过多讨论，线性化带来的误差处理方法可参见文献[5]。

4 控制算法和实例

4.1 控制算法

确定控制律的关键是求解正则方程（10），以系统进入吸引区（可线性化区域）为目标，求解微分方程（10）的初值条件λ（0），其算法流程图如图2所示。

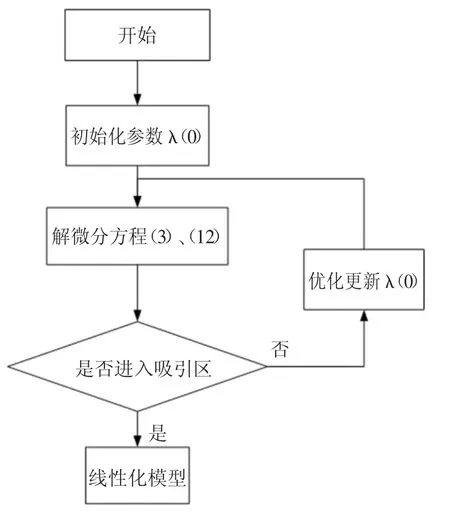
图2 确定λ（0）的算法

4.2 仿真实例[3]

以文献[3]为例，结构参数 θ1=1.333，θ2=1.33，θ3=1，θ4=14.7，θ5=9.8。摇起区采用最优控制律为τ2=-λTb，初始条件 λ（0）=[-9，-10，10，7]T。

线性化系统为[5]

其中

取吸引区性能指标[3]为

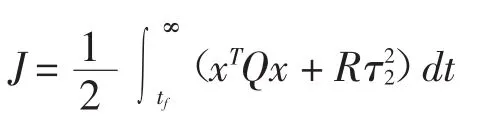
其中Q=I4，R=0.6。控制律取为状态反馈τ2=Kx，控制增益为K=-BTR-1P，其中P是下列Ricatti方程的解。

由此可得

图3 平衡区范围为π/6的仿真结果

为方便比较，列出文[3]的结果如图4所示。

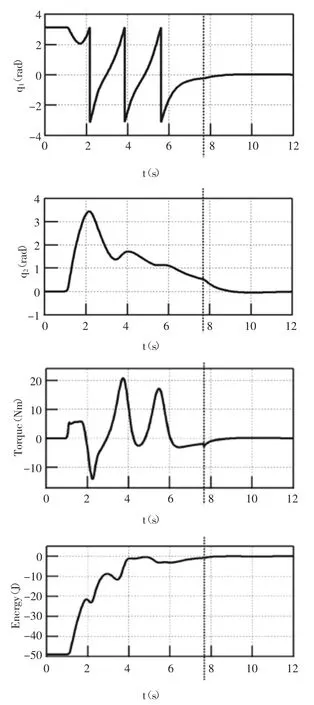
图4 文献[9]仿真结果

本文结果系统在3.25 s处切换，在5 s附近稳定，文献[3]中系统在7.66 s处切换，在9 s处稳定，本文结果优于文献[3]。

5 结论

提出了一种基于性能指标的Acrobot机器臂的控制方法，控制策略是使用最优控制律驱动系统向不变集运动，当系统运动至可线性化区域时，切换控制至LQR，使系统稳定在垂直向上平衡点。讨论了最优控制律下系统的局部稳定性和切换控制的全局稳定性，建立了控制器的算法。值得一提的是，文中控制律可能出现奇异非平凡问题（即某时段内开关函数恒为0）是将来需要进一步解决的问题。