矿用电动轮车变流系统的键合图建模与控制

陈茂林，李毅

（湖南省邮电规划设计院有限公司，湖南长沙410126）

关键字：矿用电动轮车；鲁棒性；键合图；谐振控制器；变流系统

在年开采量千万吨级以上的大型露天矿山的运输设备中，矿用电动轮自卸车已占据2/3的市场，承担着世界上40%的煤、90%的铁矿开采运输量[1]。矿用电动轮自卸车交流传动系统如图1所示，利用车载大功率柴油发动机带动同步发电机发出三相交流电，经过变流系统（包括整流器和逆变器）输出变压变频（VVVF）的三相交流电供给三相异步电机，又将电能转变成机械能输出[2]。电动轮自卸车的电源由车载大功率柴油发电机组提供，容量有限，运行工况恶劣，负荷波动大，对动力系统运行稳定性和鲁棒性要求更高，因此采用键合图建模及控制理论方法对电动轮自卸车变流系统电压和转速的综合协调优化，达到提高系统鲁棒稳定性和整车运行效率的目的。

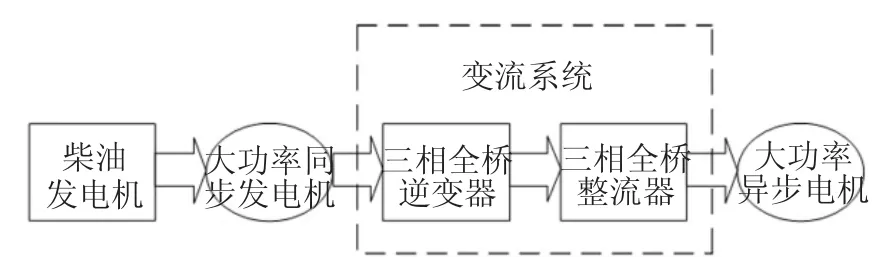
图1 交流传动系统框图

1 变流系统的描述

矿用电动轮自卸车变流系统的电气原理图如图2所示，其中柴油发电机组及同步发电机所产生的电能经过整流后可以视为一个恒定的直流电源us。为了使研究的控制方法更具通用性和鲁棒性，要求负载的变化对控制系统性能的影响不能过大，因此将逆变器和LC滤波网络作为主要的控制对象，而感应电动机则只是作为负载的一种，不同的负载有不同的功率和功率因素的要求。

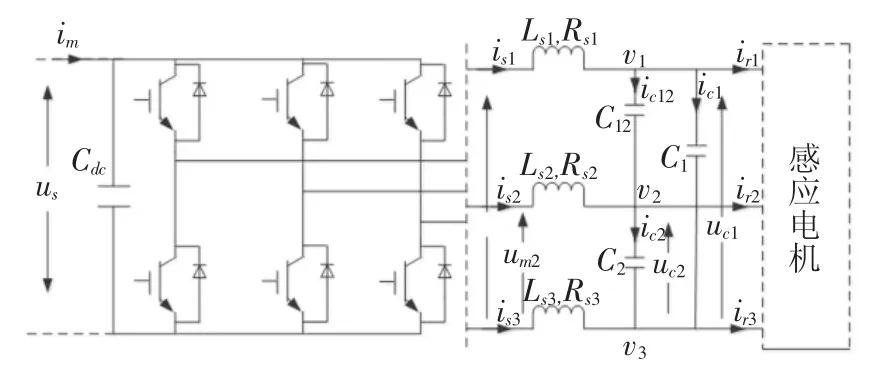
图2 逆变器与LC滤波原理图

LR滤波器是一种常见的基本滤波器，由一个电阻和一个电感串联而成，这种滤波器结构简单，但是对于矿用电动轮自卸车变流系统逆变器与电机之间的滤波，它不利于从稳定性、谐波分析的角度来分析系统的鲁棒性，所以需要一个相对复杂的滤波器，如图2所示，联接一个LC滤波器，由一个电感和电阻与电容并联而成，以其为基础，增加相应元件可以组成更为复杂的滤波器以适应于不同的应用场合，以图2为例，在LC的基础上并联一个电感可组成一个LC滤波器。滤波器的组成主要根据稳定性和谐波分析的要求而确定。

图2中需要控制的量为电感Lf1、Lf2、Lf3的电流分别为if1、if2、if3和电容 C1、C2、C12的电压。通过对这些量的控制使系统相当于一个电压源，与之相比，传统的LR结构则相当于一个电流源。

2 变流系统的键合图建模

将三相逆变器的一相作为参考电压，因此逆变器的模型只需保留两个变换单元。因此，只需对线电压um1和um2进行控制[3]。电流is3与另外两相电流is1和is2线性相关。

考虑逆变器的平均行为，因此只需研究LC滤波器上的平均作用，而不研究开关行为本身[4]。因此定义两个控制信号为：

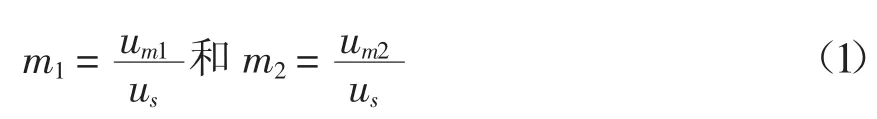
根据键合图建模的方法[5]，将矿用电动轮自卸车变流系统统经过整流器输出的直流电压us当做键合图模型的输入常量势源，三阶的LC滤波器由三个电感及电阻与三个电容器并联组成，结合前面两章键合图建模的理论得到图3的键合图模型。

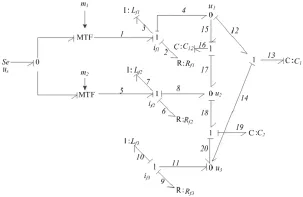
图3 变流系统的键合图模型

图3中，元件I:Lf3和元件C:C12为微分因果关系。键合图模型的键 12、15、17、18、20 和 14 构成一个因果代数环，为了消除这种因果代数环，感性元件的Lf3和容性元件的C12为微分因果关系。由键合图模型知惯性元件和感性元件一共六个，除了元件I:Lf3和元件C:C12为微分因果关系，其它四个为积分因果关系，所该模型的状态方程为四阶模型[5]。图4是包括了滤波器的负载LC的键合图模型，图中包含四个传感器（Df:if1，Df:if2，De:uc1，De:uc2）。

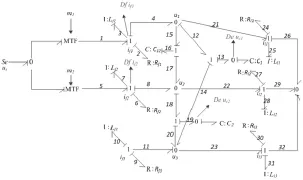
图4 连接负载的键合图模型

3 变流系统的控制

将矿用电动轮自卸车变流系统的整流器输出的电压，作为输入常量势源，三相逆变器的其中一相作为参考，另外两相以可调变换器（MTF）替代，通过对m1和m2的可调控制，达到对电容器提供的电压进行控制，对矿用电动轮自卸车变流系统进行键合图建模符合实际变流系统，并且满足控制的需要。

三相LC滤波器是一个高度耦合四阶复杂系统，但是只有m1和m2两个控制信号。为了使三相LC滤波器相当于一个电压源，必须对电容器提供的电压进行控制，因此，以双向因果键合图为基础，并根据逆键合图（Inverse Bond Graph）进行设计控制器。双向因果键合图由Gawthrop提出[6]，可用于逆系统性质的研究、状态估计和参数估计。

根据逆键合图的构成方法，需要改变键合图中流变量的探测器Df，改变之后为键合图中的源Se0Sf，因为它是势为零而且没有流流向反键合图模型。因此，改变后的键合图模型传播双向因果关系，但是只在其中的一个方向传输功率，而且传播的双向因果关系由源SS提供，双向键合图在反向键合图中变成探测器。

逆变器的键合图模型中存在逆向键合图，所以适合设计开环控制的结构，通过解耦（逆矩阵运算和扰动补偿），并锁定动态误差可以将开环控制结构扩展到闭环控制。

有两种不同的设置控制器参数的方法：

论坛上，中国食品工业协会科技质量部主任杨强对京津冀地区的酒业现状与特色做了介绍。中国质量万里行促进会刘兆彬会长就中国酒行业在2019年的发展机遇做了分析，并对白酒行业的京津冀一体化前景做了深入的解读。

1、假设感性元件I：Lfi的动态响应与容性元件C的动态响应相比较足够快。因此只要控制闭环回路的电容C1和C2的电压，电容C12元素的电压直接与C1和C2的电压相关；

2、另一种方法考虑两个回路级联，一个回路为电感Lfi的电流回路，另一个为电容Ci的电压回路。

第二种方法性能优于第一种，因此选择第二种方法计算来设计控制器，该方法分为两个步骤，首先确定电流参数，然后确定电压参数。

图5所示为系统的逆键合图，根据其可推导出开环电流控制的方法。图中，两个电流传感器通过双因果键进行因果逆转，同时得到两条不相交的双向因果路径，这两条路径分别指向控制信号（m1和m2）对应的所需逆向模型的输出，由此可以证明该模型为可逆模型[7]。

图5所示的键合图模型中可知，所有的感性元件（电感）I都为微分因果关系，根据图5及第二章所介绍的由键合图模型推导数学方程可以得到：

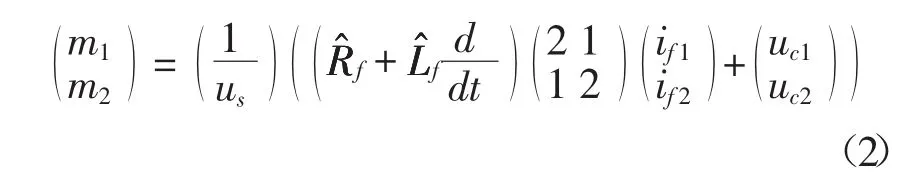
图5 电流控制法的逆向键合图

三相LC滤波器中Rfi和Lfi都为相同的数值，和为实际系统参数的估计值。为了建立闭环控制系统，在表达式（2）中设置一个动态误差ξi=ifrefi-ifi，而且 ξi+kp1ξi=0，kp1为比例增益，其值是固定的，所以式（2）变为：

整理得到：

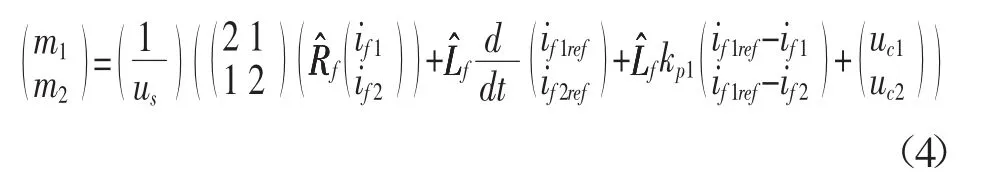
将式（4）做拉普拉斯变换得到：

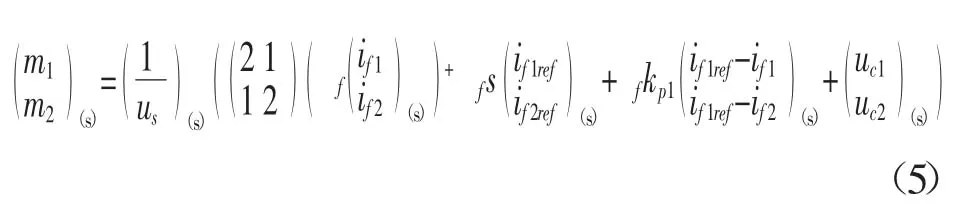
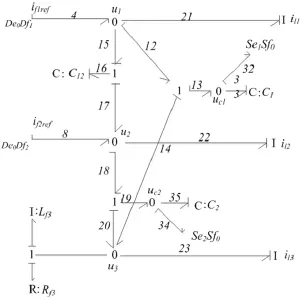
图6 电压控制的逆向键合图模型

采用与上述相同的步骤可以从图6中得到公式（6）。图中存在两条从SeiSf0到De0Dfi的不相交双向因果路径，因此该模型是可逆的，由此可得：

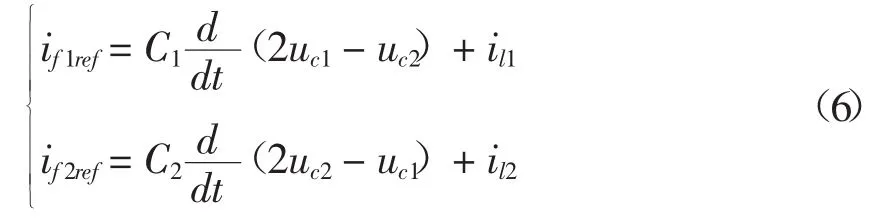
式（5）为逆变器输出电压的控制模型，实际的滤波器中三个电容器的数值都相同且为定值即C1=C2=C12=C，将其用估计值代替，则公式（6）变为：

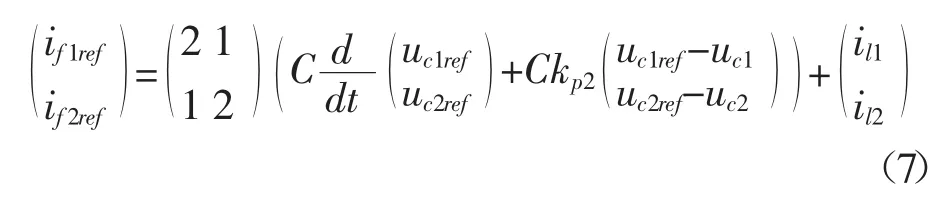
式中kp2是一个固定的比例增益，可以根据文献[8][9]将其用一个谐振控制器进行替换，如公式（8）所示：

自然频率ωn调整为输入信号的频率以获得无穷大的开环增益[10]。谐振控制器中的参数通过极点配置的方法进行设置。

将（7）进行拉普拉斯变换得到：

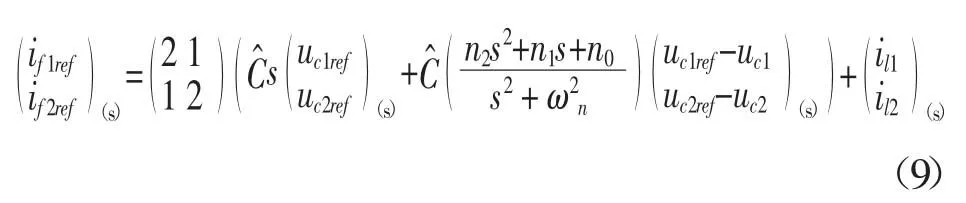
设计谐振控制器的参数时假设电流环动态是无限的，如果将电流设置为参考值，则模型变成六阶模型，包括2阶电容器和具有四阶的两个谐振控制器。六个极点为：

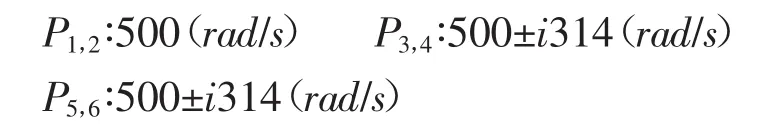
响应时间为10 ms的时间。完整模型控制器的结构框图为7所示，需要注意的是控制器包含参考输入的一个具有微分作用的前馈环节。参考信号为正弦信号，并且可以通过解析形式推导出来。三相LC滤波器作为电压源的一部分，其参数应该保持大致稳定，变化的幅度不应过大，滤波器的参数需要符合稳定的条件。反之，负载则认为可能产生非常大的变化，当其参数在大范围进行变化而不影响系统的性能时，则可认为系统具有很好的鲁棒性。

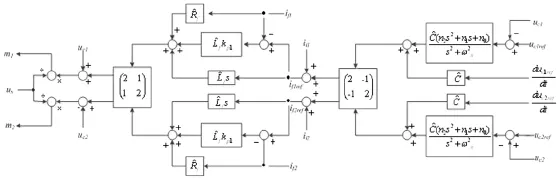
图7 正弦参考输入的逆键合图模型控制框图

4 实验结果

针对三相LC滤波器的三相LC负载，通过负载和功率因数的变化研究控制方法的鲁棒性，下面将分析两种不同功率因数下负载由0变为额定功率为5千瓦时系统的鲁棒性。

鲁棒性的分析可以用零极点图来描述，通过零极点的位置变化来说明系统的鲁棒稳定性。零极点图可以由20-sim中Frequency Domain Toolbox的Model Linearization工具直接得到[11]，如图8所示，选择输入输出变量后即可得到如图所示的界面，选择相应的选项即可得到相应的传递函数、零极点等，同时也可以直接画出Bode图、Nyquist图、零极点图等，从而使得系统的分析更加方便简洁。

仿真数据为：

图8 20-sim界面图

绘制极点时假设三相滤波器的参数存在很小的误差，模型参数的数据和控制器的参数存在10%的误差，这样更能证明由参数的不确定性来分析系统的鲁棒性。

对于第一种情况，当功率因数为零的时候，则无功功率Q不存在为空的，因此负载只有吸收有源功率P，图9给出了完整模型的极点图。

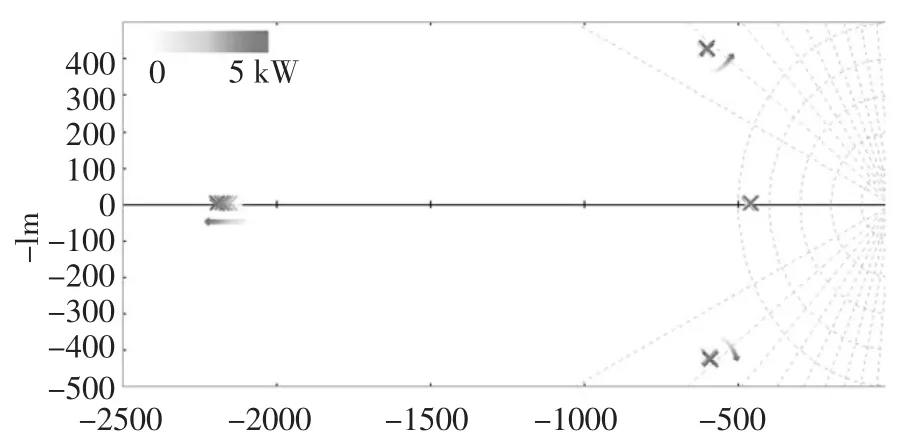
图9 功率因数PF=0时零极点图

当负载从0到5kVA的变化过程中，八个极点只有非常轻微的变化，其中变化最大的两个极点位于2000rad/s附近。电感的功率因数为PF=0.8，通过功率S表示预期的有功功率和无功功率负载，变量由无负载到5kVA。两个增加的极点对应于相应的负载，由于L/R的比值不发生改变，相对于负载来说极点不发生变动，如图10所示：

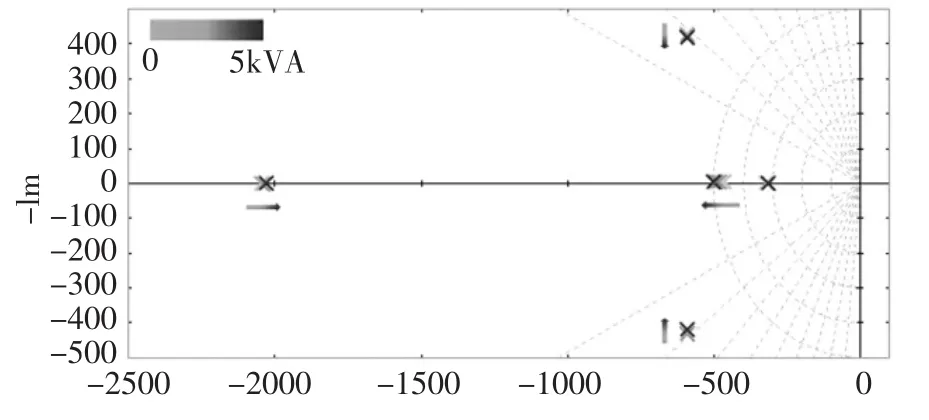
图10 功率因数PF=0.8时零极点图

在第一种情况下，负载的变化对极点的位置没有显著的影响，因此在这两种情况下，说明了控制模型具有良好的鲁棒性。

考虑最后一种情况下系统的鲁棒性，即存在一个不平衡的负载。这种情况下，假定负载为双相负载，这说明三相负载中有一相是断开的，因此只有其中两相负载。如图11所示，极点的位置由300rad/s（负载极点）变成现在的单个极点，同时我们可以看到在视在功率增加的过程中只有一个双极点（2000rad/s）的位置发生变化，其他极点的位置不发生任何改变。

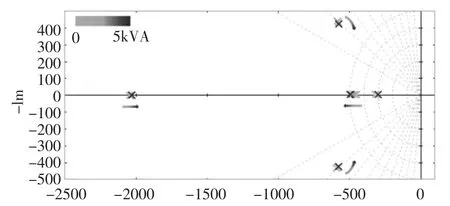
图11 功率因数PF=0.8不平衡负载时零极点图

5 结论

用键合图对LC滤波器和LC负载进行建模，推导数学方程。把LC滤波器一部分相当于电压源，LC负载结构相当于电流，最后用键合图对交流传动系统的逆变器和三相LC滤波器进行了鲁棒性分析，并且通过改变负载的功率和搭载不平衡的负载并且仿真得到的极点位置并没有发生明显改变来验证系统具有良好的鲁棒性，从而能够满足矿用电动轮车电源由车载大功率柴油发电机组提供，容量有限，运行工况恶劣，负荷波动大，对动力系统运行稳定性和鲁棒性要求。