大群体在线客户偏好自动计算方法

刘 翔

（上海大学管理学院，上海200444）

在激烈的市场竞争中，客户资源是企业的核心资源，以客户资源为核心优化配置企业资源的关键是如何发现客户偏好并将大群客户总体偏好模式充分地结合到新产品开发中，这是市场理论研究与实践的共识[1-2]。目前客户偏好的预测计算方法一般是通过互联网在线或非在线的市场调查问卷方式来完成。这种方法不仅非常耗时和昂贵，更重的是获得的数据质量很大程度上取决于问卷设计内容与接受访问的调查者的范围、类型及参与的态度等。目前在线客户偏好对产品销售策略及潜在客户的购买决策都产生了重要影响。各主流商务网站都广泛提供机会让客户自主发布客户偏好。从这些客户偏好中发现产品的优点与缺点，十分有助产品制造商面向客户需求改进产品设计并制定更适合客户需求的商务战略[3-4]。然而，客户偏好中的有价值信息通常是由广泛分布的评论文本、评分等级等大量信息碎片组成的，目前有关客户偏好的研究文献尚未能提出有效方法解决如何在大量客户偏好的客户意见中低成本、快速地发现客户总体偏好[5-10]。本文提出了一个称为面向大型群决策的自动一致性模型（Automatic Consensus Model for Large Group Decision-making，简称 ACMLGD），用于低成本、快速地自动计算面向在线客户偏好的大群客户偏好。因此，本文的研究工作具有很强的理论与实践意义。

大型群决策是一种广泛存在的决策活动，例如在复杂商务决策，尤其在ERP及B2B等复杂协同决策领域有极为重要理论研究及商业应用价值。大型群决策通常包括二个过程：一致性过程与选择过程[11-13]。现仅有极少量的大型群决策中的一致性过程研究文献，而这些文献对该问题的理解又十分模糊与混乱[14-17].Alonso et al.（2009）提出了一种模糊的大型群决策模型，采用诱导有序加权平均（IOWA）算子集结个体决策专家偏好及确定方案的排序方法。Carvalho et al.（2011）开发一个支持大型群决策的系统。Palomares et al.（2014）提出了探测和管理大型群体决策的非合作行为的一致性模型，其中，采用基于模糊聚类的模式探测非合作的个体或子组。基于Palomares et al.（2014）的方法，Xuan et al.（2015）提出了一种改进的大型群体应急决策的一致模型，其中，可管理少数个体意见及非合作行为。Quesada et al.（2015）提出了一种在大型群决策一致性过程中管理参与者行为的方法大集团的决策，克服了Palomares et al.（2014）方法的不足：参与者权重不能再增加，即使他们改变了想法和决定采取更加合作的态度。然而，采用以上方法需要手工返回各种意见给个体决策专家并适当修改个体意见，直到获取合理的群一致性。显然，在一致性过程中，不可能要求客户偏好用户反复修改个体意见。因此，采用以上方法来计算面向在线客户偏好的大群客户偏好是不可行的。

关键创新和贡献是提出一种新的、类似研究中没有出现过的面向大型群决策的自动一致性方法（简称ACMLGD）用于自动计算面向在线客户偏好的大群客户偏好。其中，采用了人工蜂群优化算法优化个体的权重与群组权重方法以达到个体之间意见一致性最大化，并结合仿真一致性达成过程，预先设置确定优化的一致性过程的重要参数，以实现在有限时间内达到合理一致性的大群客户偏好计算目的。人工蜂群优化算法具有全局优化的杰出能力而获得大量应用，如神经网络训练、预测股票市场。人工蜂群优化算法超越其他类似的启发式优化算法，如遗传算法与粒子组优化等[18-20]。

实验结果表明，ACMLGD模型在大量客户偏好的客户意见中发现客户总体偏好的计算性能较好。为在线客户偏好的大群客户偏好自动集结建模及应用提供了一种新的实用方法。

后续部分组织如下：第2节是问题的描述。第3节研究提出的自动一致性模型。第4节研究大群客户偏好计算应用实例。最后，结束语。

1 问题描述

针对从互联网上采集的大量有关产品消费者发布的有正面评价、负面评价及打分等的意见，结合文本挖掘和情感分析技术，提取在线评论中正面评价、反面评价及综合评分等信息，并将这些有价值的信息碎片转封装为能对多种产品进行综合评价的不同的、独立的信息粒度。如果将每个达到产品专家评论水平的信息粒度定义为表示相应参与大群型决策的专家信息与意见，则面向在线客户偏好的大群客户偏好计算可转化为面向大型群决策的自动一致性建模与求解过程问题。第4节将用实例来说明该转换思想。基于文献[11，12，17]，现有的自动一致性方法基本思想描述如下：

（i）假定群决策专家组集合为E={E1，E2，…，Er}。其中，Ey（y=1，2，…，r）是第y子组。设λ=（λ1，λ2，…，λr）T为子组Ey（y=1，2，…，r）的权重向量，其中设X=（x1，x2，…，xr）T为子组Ey（y=1，2，…，r）成员数向量，其中Xy（y=是群决策专家组集合E中总的专家数）是子组Ey（y=1，2，…，r）中专家总数。个体决策专家的权重为其中

（ii）假定群决策问题有明确的备选可行方案集A={a1，a2，…，an}（n≥2）。

（iii）假定群决策问题的决策标准集为U={u1，u2，…，um}，且有标准的权重向量为w=（w1，w2，…，

（v）设个体标准决策矩阵 Dk=（dijk）m×n（i=1，2，...，m，j=1，2，…，n，y=1，2，…，r，k=1，2，…，N）通过加权集结算子转化为群决策矩阵D=（dij）m×n（i=1，2，...，m，j=1，2，…，n），其中，dij=

（vi）为了测量个体标准决策矩阵 Dk=（dijk）m×n（i=1，2，...，m，j=1，2，…，n，y=1，2，…，r，k=1，2，…，N）与群决策矩阵D=（dij）m×n（i=1，2，...，m，j=1，2，…，n）之间一致性，设 c 为一致性迭代次数，迭代系数为0<η<1，计算Dk=（dijk）m×n（i=1，2，...，m，j=1，2，…，n）与D=（dij）m×n（i=1，2，...，m，j=1，2，…，n）之间不一致性，即，

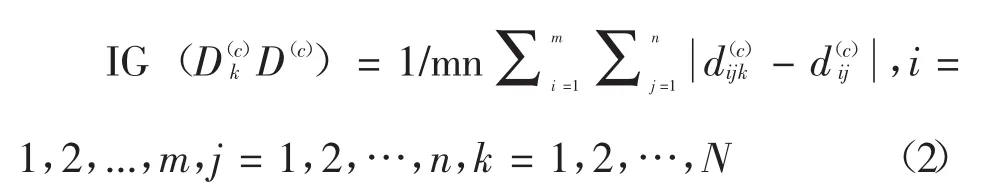
如果任意IG（D（c）kD（c））≤δ（i=1，2，...，m，j=1，2，…，n，k=1，2，…，N），那么一致性过程可以停止。否则，令D（c+1）k=（d（c+1）ijk）m×n与D（c+1）=（d（c+1）ij）m×n。其中，

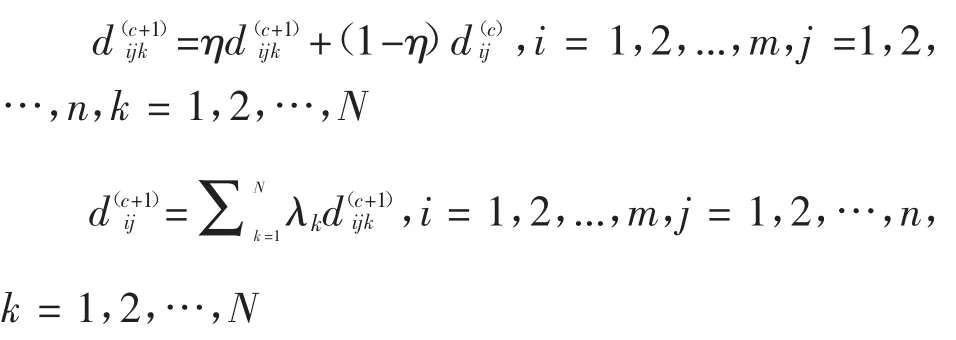
然后，令 c=c+1，根据公式（2）继续计算。

根据文献[11]，该算法是收敛性的，在群决策中应用该方法可辟免强制个体决策专家手工修改其意见。然而，在群体较大及一致性要求较高的情况下，以上方法迭代次数是非常大的，会导致进入一个非常耗时的或无限循环的一致性达成过程中。此外，根据文献[21]，该算法还存在一些其它不足，如在一致性过程结束后得到一致性群决策矩阵是由初始个体决策矩阵生成的。本文涉及的问题是如何有效自动管理大群客户偏好，辟免一致性过程进入非常耗时的循环并自动生成能反映大群一致性不断进化结果的一致性群决策矩阵。

2 自动一致性模型

2.1 模型假设

基于文献[9，10，11，12，17]，本文提出了改进的自动一致性模型ACMLGD框架如下：

（i）假定群决策专家组集合为E={E1，E2，…，Er}。其中，Ey（y=1，2，…，r）是第y子组。设λ=（λ1，λ2，…，λr）T为子组Ey（y=1，2，…，r）的权重向量，其中设X=（x1，x2，…，xr）T为子组Ey（y=1，2，…，r）成员数向量，其中Xy（y=11是群决策专家组集合E中总的专家数）是子组Ey（y=1，2，…，r）中专家总数。个体决策专家的权重为其中

（ii）假定群决策问题有明确的备选可行方案集A={a1，a2，…，an}（n≥2）。

（iii）假定群决策问题的决策标准集为U={u1，u2，…，um}，且有标准的权重向量为w=（w1，w2，…，

（xy）=N）转化为个体标准决策矩阵，即，

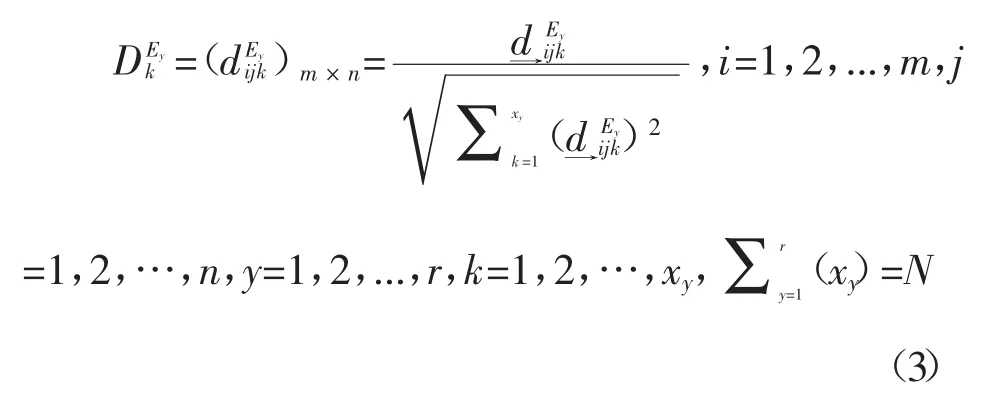
（vi）设D=（di）jm×（ni=1，2，...，m，j=1，2，…，n）表示群决策专家组集合E群决策矩阵。子组Ey（y=1，2，…，r）群决策矩阵m，j=1，2，…，n，y=1，2，…，r）通过加权集结算子转化为群决策专家组集合E群决策矩阵D=（di）jm×（ni=1，2，...，m，j=1，2，…，n），其中

（vii）大型群一致性分为三层，包括个体-子组的一致性IC，子组-群的一致性SC及个体-群的一致性GC（总体层一致性），分别定义如下：

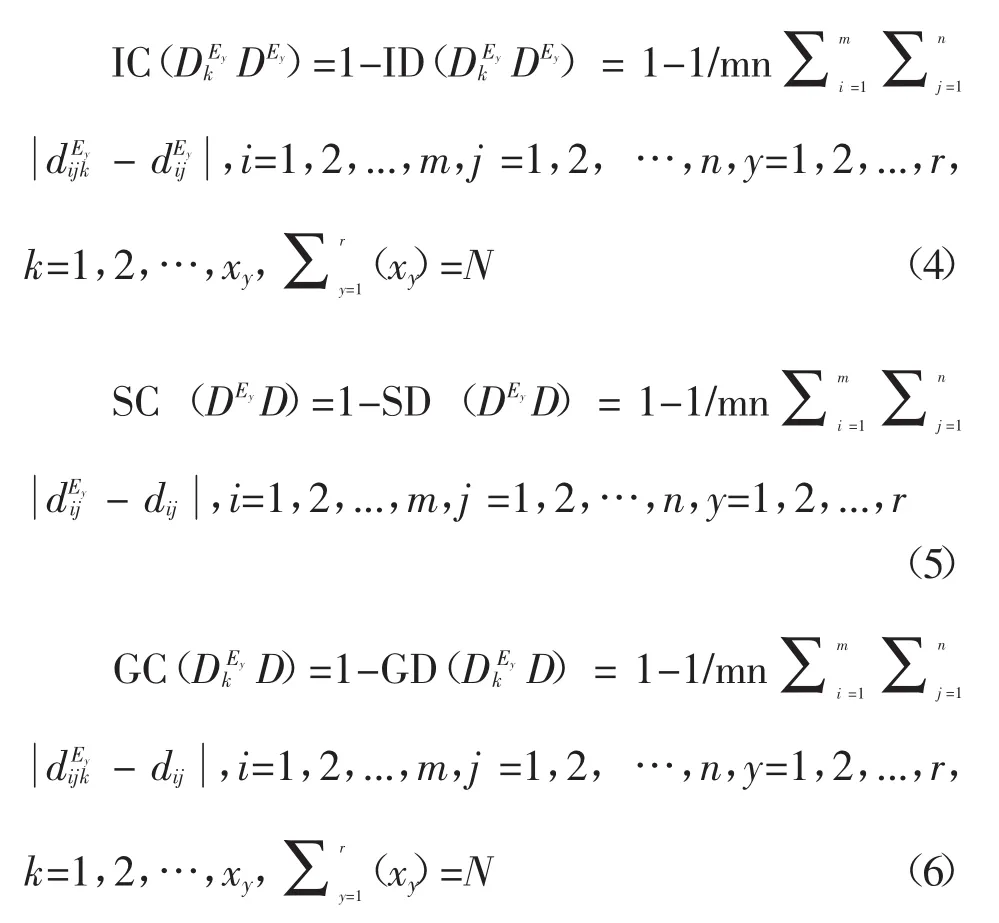
SD（DEyD）（y=1，2，…，r）表示子组Ey（y=1，2，…，r）决策矩阵DEy（y=1，2，…，r）与群决策专家组集合E群决策矩阵D之间的不一致性（曼哈顿距离）。

2.2 自动一致性过程

ACMLGD自动群一致性过程设计如下：第一步：确定大群决策的标准与初始方案

设标准集 U={u1，u2，…，um}为群决策问题的多目标，并依据问题性质确定相关指标集UA={aij}（i=1，2，…，m，j=1，2，…，n）及备选的可行方案集A={a1，a2，…，an}（n≥2）。

第二步：自动一致性建模与优化

（iv）通过加权集结算子将子组Ey（y=1，2，…，r）群决策矩阵1，2，…，n，y=1，2，…，r）转化为组E 群决策矩阵D=（dij）m×（ni=1，2，...，m，j=1，2，…，n，y=1，2，…，r），其中…，n，y=1，2，…，r）。

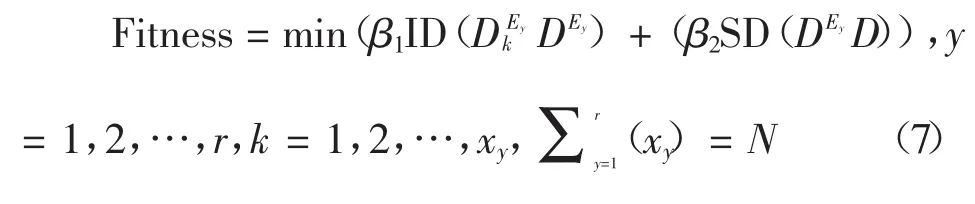
其中，Fitness表示用适度函数值来评价仿真一致性达到过程中全局一致性水平；参数β1与β2可依据问题实际情况适当调整ID（DEy与SD（DEyD）值。仿真与优化结果，将得到全局最优的群决策重要参数 δ*，C*，（y=1，2，…，r，k=1，2，…，xy，

第三步：自动一致性过程

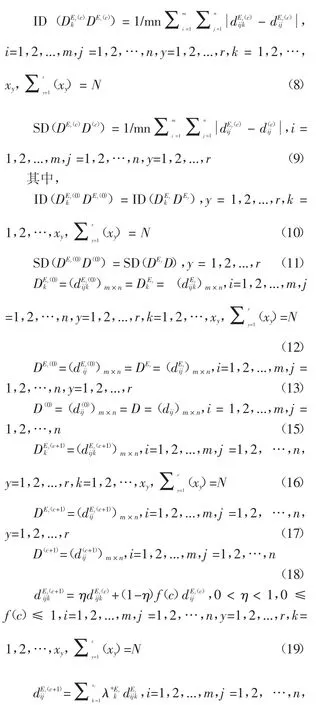
第四步：选择最优方案

第五步：结束。

3 大群客户偏好计算实例

应用所提出的ACMLGD结合文本挖掘和情感分析技术，提取在线评论中正面评价、反面评价及综合评分等信息开发了自动一致性系统，该一致性系统可集成到现有的ERP系统中，用于支持企业的大型群决策活动，也可用于集结互联网产品用户偏好、挖掘发现客户总的一致性意见。现以自动计算面向在线客户偏好的大群客户偏好为例，说明ACMLGD的应用。

3.1 问题描述

本实验采集了于2015年4月-2016年4月的1，500条有关4个主流品牌手机客户偏好数据。这些评论包括有正面评价、负面评价及评分等级，例如表1所示。

表1 手机客户偏好数据示例

首先，对这些数据作进一步预处理，步骤如下[2，10]：

1.将有正面评价与负面评价的评论数据划分为词与词组。

2.取消那些没有明确的情感极性及产品属性的词与词组（例如表示1中的“没有别的”）。

3.合并重复的词与词组（例如“超级的相机”与“好的相机”归入“相机”类）。

4.将模糊的候选属性（例如，“昂贵”）转化为明确的候选属性（价格）。

5.合并同义词（例如，“蓄电池”和“电池”）。

6.消除那些频度很低的候选属性（例如，频度小于1%）。

7.用属性集合对汇总的正面评价与负面评价进行编码。

依据以上数据预处理步骤得到有10个属性的1200条评论数据结果如表2所示。

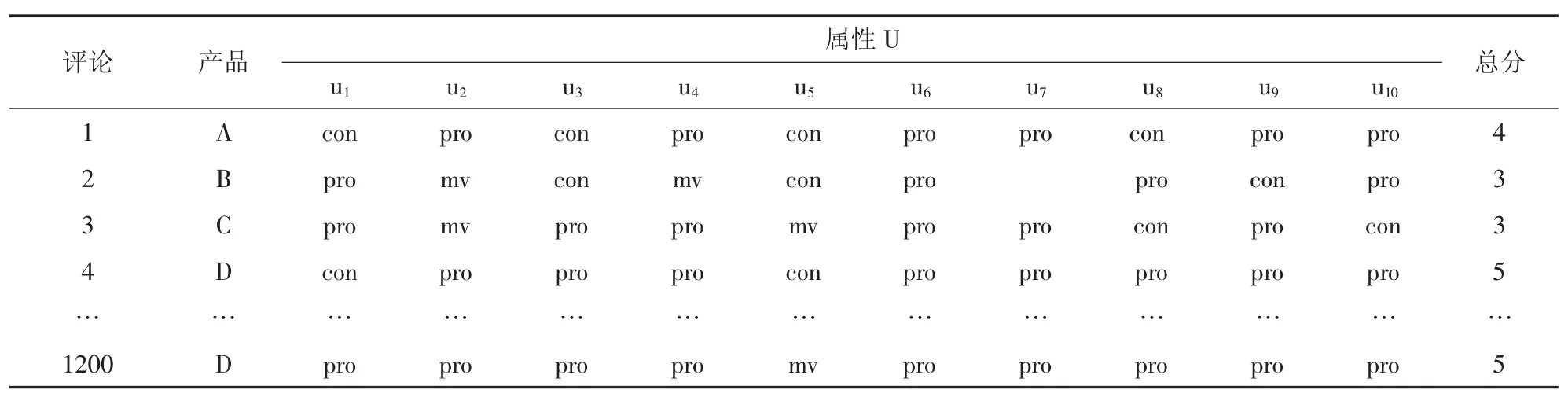
表2 数据预处理结果

然后，这些广泛分布的评论文本、评分等级等大量信息碎片预处理结果存入ERP数据库后，自主开发的自动一致性系统将以上编码后的客户偏好数据进一步规范化、合并与封装为能对多种产品进行综合评价的80个不同的、独立的信息粒度，其中，每个信息粒度均分别包含有对4个产品的评论内容。因此，每个信息粒度可看作等同于一个用户分别对4个产品的进行评论。自主开发的自动一致性系统定义每个信息粒度表示为相应虚拟个体决策专家，并自动生成个体专家的初始权重，再将已定义生成的80个体决策专家进行分组并生成各组的初始权重，分组统计的结果可从ERP数据库中查询获得，表3所示。

因此，如上依据客户偏好数据挖掘客户总偏好的过程可转化为本文提出的有80个专家参与的自动大型群决策问题。限于篇幅，省略以上信息粒度封装及统计分组的详细过程。

表3 从ERP数据库中查询获得的80个虚拟个体决策专家及分组信息

3.2 大群客户偏好一致性计算过程及结果

基于ACMLGD的自动群一致性过程与选择，即大群客户偏好一致性计算过程设计如下：

第一步：确定大群决策的标准与初始方案

将产品主要属性作为标准，确定的相关指标及初始方案集表4所示。

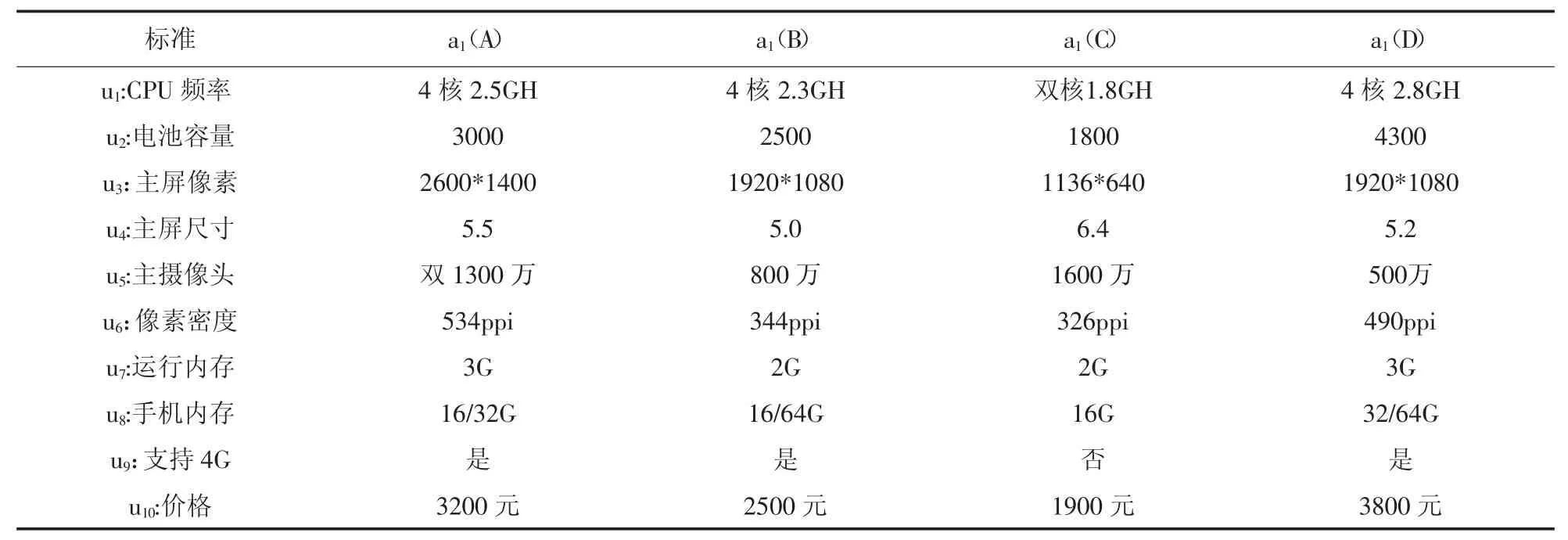
表4 基于标准 U={u1，u2，u3，u4，u5，u6，u7，u8，u9，u10}及相关指标 UA={aij}（i=1，2，...，10，j=1，2，3，4）方案集 A={a1，a2，a3，a4}

第二步：自动一致性建模与优化

（i）10 个标准，U={u1，u2，u3，u4，u5，u6，u7，u8，u9，u10}及相应权重向量 w=（0.12，0.1，0.1，0.11，0.1，0.08，0.1，0.09，0.1，0.1）T。

（ii）查询ERP数据库可获得子组Ey（y=1，2，…，10）的初始权向量，λ =（0.1009，0.1115，0.0109，0.1032，0.1005，0.1219，0.1006，0.1054，0.1224，0.1227）T。

（iii）查询ERP数据库可获得子组Ey（y=1，2，…，10）中的专家数向量，X=（3，8，8，10，10，10，8，10，7，6）T。

（iv）方案集 A={a1，a2，a3，a4}由 80 个专家（xy）=80）进行评价。

（v）预设的专家评价等级集合，S={1，2，3，4，5}（1:最差的；5:最好的）。

（vi）c=0，η =0.5 与 β1= β2=0.5。

表5 初始决策矩阵y=1，2，3，4，5，6，7，8，9，10，k=1，2，…，xy， =80）

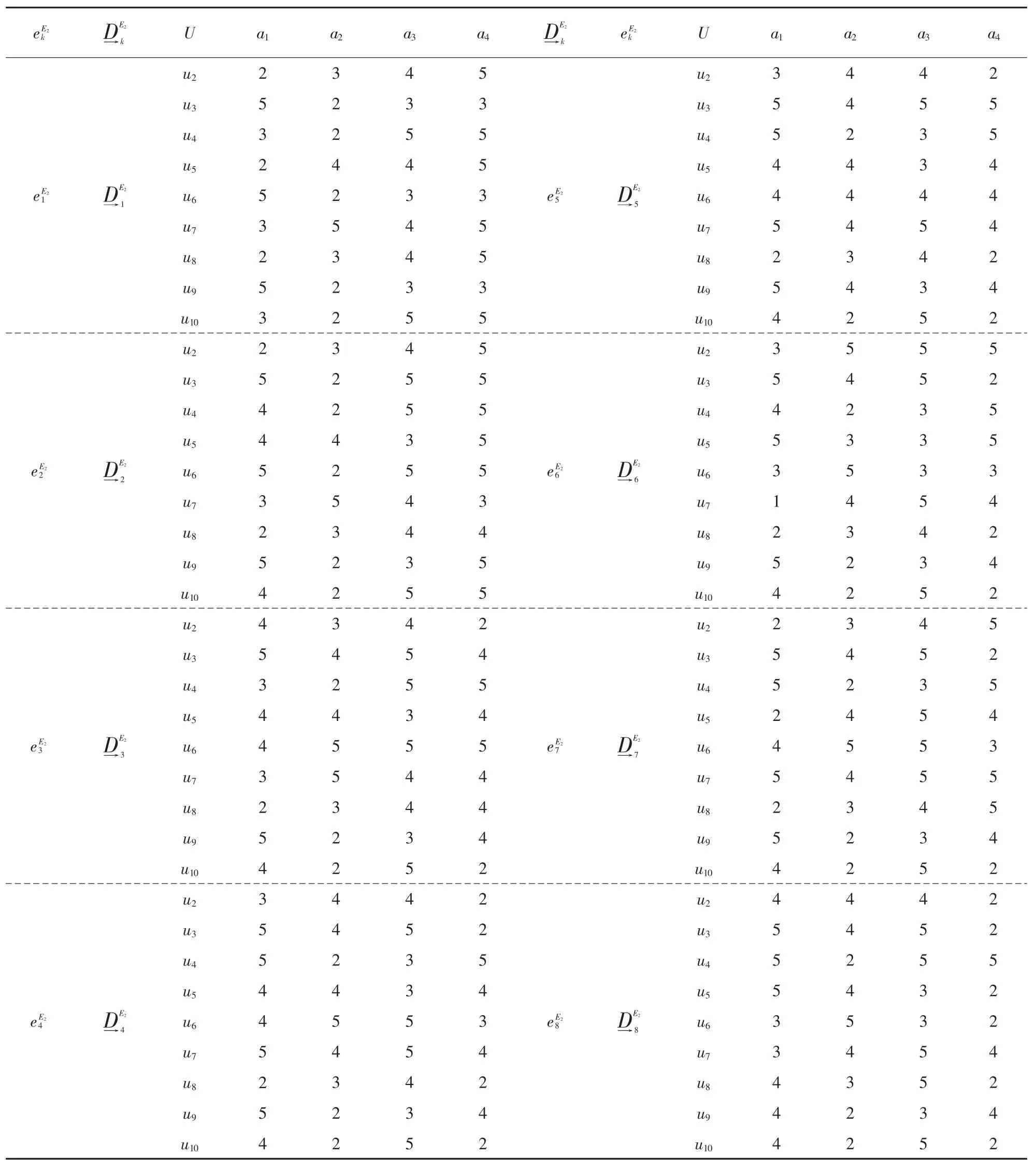
表5 初始决策矩阵y=1，2，3，4，5，6，7，8，9，10，k=1，2，…，xy， =80）

注意：其中 k=1，2，…，xy，y=2，xy=8，为了节省篇幅，其它初始决策矩阵说明省略。

eE2 k D eE2 E2 k U a1 a2 a3 a4 DE2 k k U a1 a2 a3 a4 u2 2 3 4 5u2 3 4 4 2 eE21 D eE2 E2 1 u3 5 2 3 3 u3 5 4 5 5 u4 3 2 5 5 u4 5 2 3 5 u5 2 4 4 5 u5 4 4 3 4 u6 5 2 3 3 u6 4 4 4 4 u7 3 5 4 5 u7 5 4 5 4 u8 2 3 4 5 u8 2 3 4 2 u9 5 2 3 3 u9 5 4 3 4 u10 3 2 5 5 u10 4 2 5 25 DE2 5 u2 3 5 5 5 u3 5 2 5 5 u3 5 4 5 2 u4 4 2 5 5 u4 4 2 3 5 u5 4 4 3 5 u5 5 3 3 5 u6 5 2 5 5 u6 3 5 3 3 u7 3 5 4 3 u7 1 4 5 4 u8 2 3 4 4 u8 2 3 4 2 u9 5 2 3 5 u9 5 2 3 4 u10 4 2 5 5 u10 4 2 5 2 u2 2 3 4 5 eE22 D eE2 E2 26 DE2 6 u2 2 3 4 5 u3 5 4 5 4 u3 5 4 5 2 u4 3 2 5 5 u4 5 2 3 5 u5 4 4 3 4 u5 2 4 5 4 u6 4 5 5 5 u6 4 5 5 3 u7 3 5 4 4 u7 5 4 5 5 u8 2 3 4 4 u8 2 3 4 5 u9 5 2 3 4 u9 5 2 3 4 u10 4 2 5 2 u10 4 2 5 2 u2 4 3 4 2 eE23 D eE2 E2 37 DE2 7 u2 4 4 4 2 u3 5 4 5 2 u3 5 4 5 2 u4 5 2 3 5 u4 5 2 5 5 u5 4 4 3 4 u5 5 4 3 2 u6 4 5 5 3 u6 3 5 3 2 u7 5 4 5 4 u7 3 4 5 4 u8 2 3 4 2 u8 4 3 5 2 u9 5 2 3 4 u9 4 2 3 4 u10 4 2 5 2 u10 4 2 5 2 u2 3 4 4 2 eE24 D eE2 E2 48 DE2 8

（x）通过加权集结算子将子组Ey（y=1，2，…，10）群决策矩阵y=1，2，…，10）转化为组E群决策矩阵D=（dij）m×n（i1，2，...，10，j=1，2，3，4，y=1，2，…，10）。

（xi）人工蜂群优化算法及一致性过程仿真结果表6-7所示。据问题实际情况，结合仿真结果，可确定个体决策专家的优化权重（i=1，2，...，10，（xy）=80）、子组群的优化权重（y=1，2，…，10）、一致性阀δ*及最大循环次数C*。其中，C*=300，δ*=0.2。

表6 人工蜂群优化算法及一致性过程仿真结果 C*，δ*与（y=1，2，...，10）

表6 人工蜂群优化算法及一致性过程仿真结果 C*，δ*与（y=1，2，...，10）

C* δ* λ*1λ*2 λ*3 λ*4 λ*5 λ*6 λ*7 λ*8 λ*9 λ*10360 0.1893 0.3212 0.1101 0.0103 0.1271 0.1108 0.0132 0.1012 0.0107 0.0842 0.1112240 0.2000 0.2202 0.1302 0.0552 0.1201 0.1055 0.0432 0.0908 0.0707 0.0822 0.0819180 0.2409 0.2032 0.1203 0.0672 0.1141 0.1205 0.0901 0.0618 0.0547 0.0649 0.1032

表7 人工蜂群优化算法及一致性过程仿真结果（i=1，2，...，10，j=1，2，3，4，y=1，2，…，10，k=1，2，…，xy，=80）

Y=1 Y=2 Y=3 Y=4 Y=5 Y=6 Y=7 Y=8 Y=9 Y=10 C*=380 δ*=0.1893 K=1 0.4563 0.1087 0.2303 0.1332 0.0939 0.1034 0.1254 0.0957 0.2006 0.3113 K=2 0.3412 0.1142 0.0991 0.1511 0.1653 0.1056 0.1515 0.0963 0.1212 0.0935 K=3 0.2025 0.1401 0.0924 0.1064 0.1104 0.1091 0.1224 0.0675 0.0989 0.1226 K=4 0.2002 0.0963 0.0835 0.0908 0.1214 0.0968 0.0917 0.1254 0.0894 K=5 0.1355 0.1103 0.0643 0.0906 0.1218 0.0985 0.0961 0.2213 0.1576 K=6 0.0945 0.1204 0.1467 0.0665 0.0803 0.1305 0.1033 0.0968 0.2256 K=7 0.1005 0.1201 0.0504 0.0765 0.0803 0.1327 0.1154 0.1358 K=8 0.1063 0.1311 0.0762 0.0709 0.0715 0.1422 0.1201 K=9 0.0895 0.1314 0.1079 0.0987 K=10 0.0987 0.1037 0.0987 0.1152 Total 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 C*=300 δ*=0.2000 K=1 0.4509 0.0951 0.0988 0.1408 0.0765 0.0821 0.1008 0.1009 0.1242 0.1257 K=2 0.3607 0.1032 0.1256 0.1023 0.1046 0.1123 0.1206 0.1244 0.1307 0.2115 K=3 0.1884 0.0978 0.1357 0.0915 0.0986 0.1024 0.0853 0.1003 0.1122 0.1268 K=4 0.1252 0.1418 0.1325 0.1221 0.0965 0.1425 0.0777 0.1331 0.1227 K=5 0.1481 0.1409 0.0873 0.1009 0.0992 0.0901 0.0983 0.1062 0.1786 K=6 0.0965 0.1267 0.1005 0.1204 0.1045 0.2005 0.1232 0.2504 0.2347 K=7 0.1287 0.0987 0.0721 0.1093 0.1108 0.1568 0.0927 0.1432 K=8 0.2054 0.1318 0.0602 0.0883 0.0883 0.1034 0.1045 K=9 0.1125 0.1245 0.1005 0.0991 K=10 0.1003 0.0548 0.1034 0.0789 Total 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 C*=180 δ*=0.2409 K=1 0.4443 0.0909 0.1056 0.1102 0.1209 0.1211 0.0881 0.1025 0.1453 0.2765 K=2 0.3781 0.0977 0.1335 0.0832 0.0854 0.0924 0.1337 0.0942 0.1284 0.1311 K=3 0.1776 0.1221 0.1009 0.1172 0.1004 0.1231 0.1005 0.0552 0.0943 0.1206 K=4 0.1801 0.1212 0.0881 0.1115 0.0902 0.1207 0.0852 0.1543 0.1205 K=5 0.1502 0.1058 0.1211 0.0658 0.0772 0.0786 0.0943 0.0987 0.1306 K=6 0.1018 0.1321 0.1036 0.1022 0.0835 0.1985 0.1202 0.2119 0.2207 K=7 0.1231 0.2007 0.1209 0.0983 0.1003 0.1445 0.0915 0.1671 K=8 0.1341 0.1002 0.1111 0.1453 0.1227 0.1354 0.0917 K=9 0.0725 0.0901 0.1231 0.0951 K=10 0.0721 0.0801 0.0664 0.1701 Total 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000

第三步：自动一致性过程

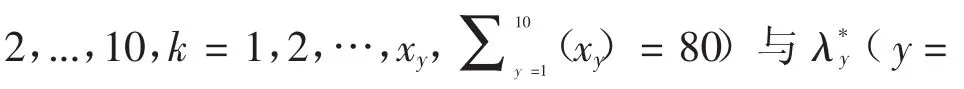
通过公式（8），（9）及全局最优控制参数C*=1，2，...，10）计算ID（i=1，2，...，10，j=80）与SD（DEy（0）D（0））（y=1，2，...，10）。计算结果表8所示。

表8 ID =80）与SD（DE（y0）D（0））（y=1，2，...，10）的计算结果

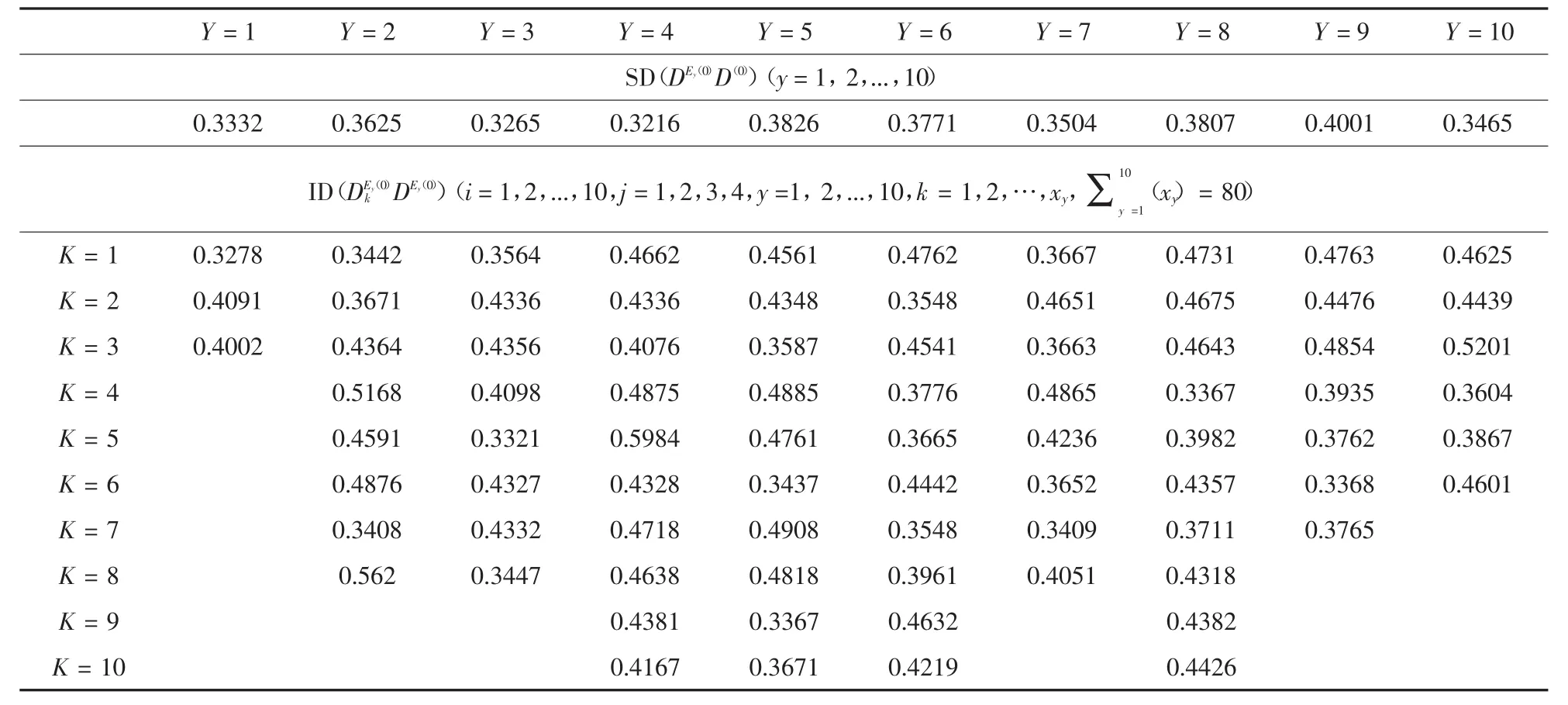
表8 ID =80）与SD（DE（y0）D（0））（y=1，2，...，10）的计算结果

（xy）=80）K=1 0.3278 0.3442 0.3564 0.4662 0.4561 0.4762 0.3667 0.4731 0.4763 0.4625 K=2 0.4091 0.3671 0.4336 0.4336 0.4348 0.3548 0.4651 0.4675 0.4476 0.4439 K=3 0.4002 0.4364 0.4356 0.4076 0.3587 0.4541 0.3663 0.4643 0.4854 0.5201 K=4 0.5168 0.4098 0.4875 0.4885 0.3776 0.4865 0.3367 0.3935 0.3604 K=5 0.4591 0.3321 0.5984 0.4761 0.3665 0.4236 0.3982 0.3762 0.3867 K=6 0.4876 0.4327 0.4328 0.3437 0.4442 0.3652 0.4357 0.3368 0.4601 K=7 0.3408 0.4332 0.4718 0.4908 0.3548 0.3409 0.3711 0.3765 K=8 0.562 0.3447 0.4638 0.4818 0.3961 0.4051 0.4318 K=9 0.4381 0.3367 0.4632 0.4382 K=10 0.4167 0.3671 0.4219 0.4426 Y=1 Y=2 Y=3 Y=4 Y=5 Y=6 Y=7 Y=8 Y=9 Y=10 SD（DEy（0）D（0））（y=1，2，...，10）0.3332 0.3625 0.3265 0.3216 0.3826 0.3771 0.3504 0.3807 0.4001 0.3465 ID（DEy（0）kDEy（0））（i=1，2，...，10，j=1，2，3，4，y=1，2，...，10，k=1，2，…，xy，Σ10 y=1

由于对任意i=1，2，...，10，j=1，2，3，4，y=1，有因此，令c=c+1，进一步计算与SD（DEy（0）D（0））（y=1，2，...，10）。经过288次迭代后，计算结果表9所示。

表9 =80）与SD（DE（y0）D（0））（y=1，2，...，10）的计算结果

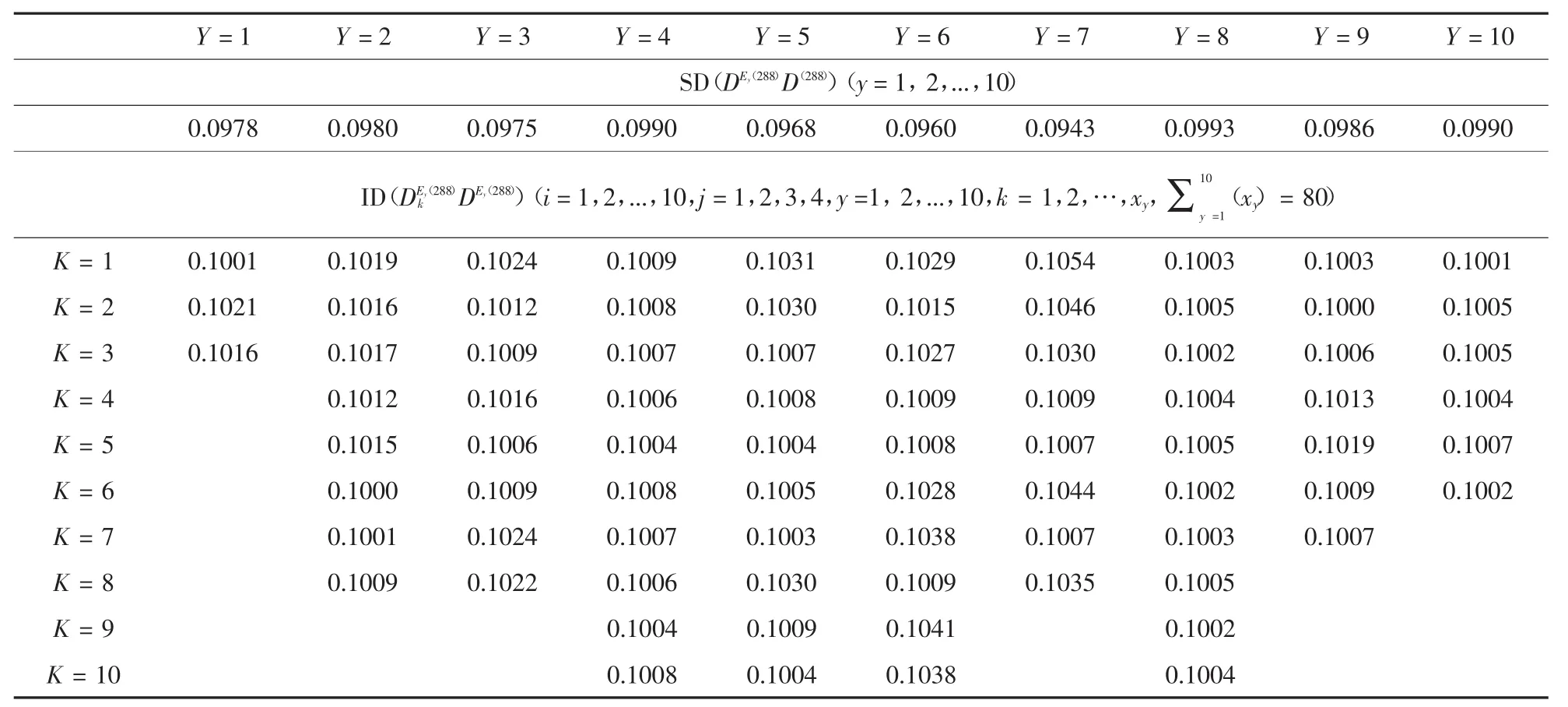
表9 =80）与SD（DE（y0）D（0））（y=1，2，...，10）的计算结果

（xy）=80）K=1 0.1001 0.1019 0.1024 0.1009 0.1031 0.1029 0.1054 0.1003 0.1003 0.1001 K=2 0.1021 0.1016 0.1012 0.1008 0.1030 0.1015 0.1046 0.1005 0.1000 0.1005 K=3 0.1016 0.1017 0.1009 0.1007 0.1007 0.1027 0.1030 0.1002 0.1006 0.1005 K=4 0.1012 0.1016 0.1006 0.1008 0.1009 0.1009 0.1004 0.1013 0.1004 K=5 0.1015 0.1006 0.1004 0.1004 0.1008 0.1007 0.1005 0.1019 0.1007 K=6 0.1000 0.1009 0.1008 0.1005 0.1028 0.1044 0.1002 0.1009 0.1002 K=7 0.1001 0.1024 0.1007 0.1003 0.1038 0.1007 0.1003 0.1007 K=8 0.1009 0.1022 0.1006 0.1030 0.1009 0.1035 0.1005 K=9 0.1004 0.1009 0.1041 0.1002 K=10 0.1008 0.1004 0.1038 0.1004 Y=1 Y=2 Y=3 Y=4 Y=5 Y=6 Y=7 Y=8 Y=9 Y=10 SD（DEy（288）D（288））（y=1，2，...，10）0.0978 0.0980 0.0975 0.0990 0.0968 0.0960 0.0943 0.0993 0.0986 0.0990 ID（DEy（288）kDEy（288））（i=1，2，...，10，j=1，2，3，4，y=1，2，...，10，k=1，2，…，xy，Σ10 y=1

由于对任意i=1，2，...，10，j=1，2，3，4，y=1，Ey（288））+SD（DEy（288）D（288））＜0.2，因此，群决策矩阵D（288）=（）10×4是全局一致性可接受的决策矩阵，表10所示。

表10 全局一致性可接受的决策矩阵D（288）=（）10×4

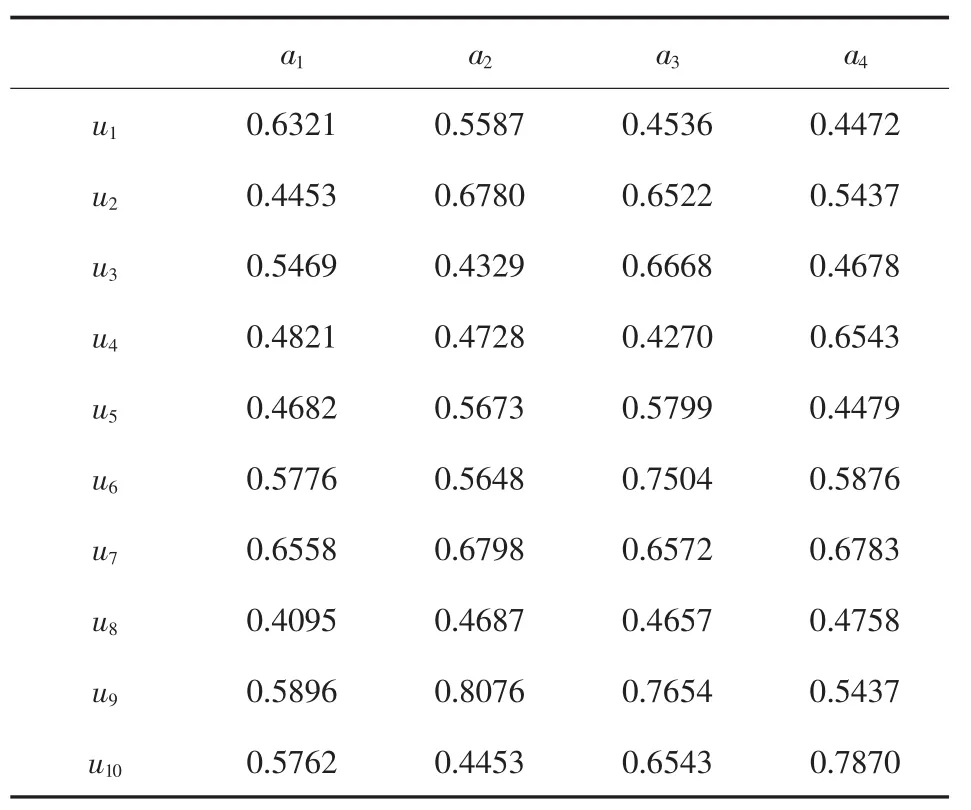
表10 全局一致性可接受的决策矩阵D（288）=（）10×4

a1 a2 a3 a4 u1 0.6321 0.5587 0.4536 0.4472 u2 0.4453 0.6780 0.6522 0.5437 u3 0.5469 0.4329 0.6668 0.4678 u4 0.4821 0.4728 0.4270 0.6543 u5 0.4682 0.5673 0.5799 0.4479 u6 0.5776 0.5648 0.7504 0.5876 u7 0.6558 0.6798 0.6572 0.6783 u8 0.4095 0.4687 0.4657 0.4758 u9 0.5896 0.8076 0.7654 0.5437 u10 0.5762 0.4453 0.6543 0.7870

第四步：选择最优方案

（i）采用公式（23）对一致性群决策矩阵 D（288）=（D（288）ij）10×4（i=1，2，...，10，j=1，2，3，4）的第j列进行汇总，得到方案aj（j=1，2，3，4）总的评价值D（288）j（j=1，2，3，4），计算结果表11 所示。

表11 方案aj（j=1，2，3，4）总的评价值j=1，2，3，4）

表11 方案aj（j=1，2，3，4）总的评价值j=1，2，3，4）

aj a1 a2 a3 a4 D（288）jD（288）1D（288）2D（288）3D（288）4总的评价值 5.3833 5.6759 6.0725 5.6333排序 4 2 1 3

表12 产品3是基于2015年4月-2016年4月的1，500条有关4个主流品牌手机客户偏好数据挖掘发现，80%以上的客户偏爱的手机产品

第五步：结束。

3.3 结果讨论

ACMLGD模型在大量产品评论的客户意见中发现客户总体偏好的计算性能通常采用在有限时间内达到预定的一致性水平来衡量。因此，ACMLGD模型在大量产品评论的客户意见中发现客户总体偏好的敏感性分析与性能比较，一般研究达到预定义一致性水平的阀与循环次数对方案排序影响。在ACMLGD方法下，不同的预定义一致性水平阀与迭代循环次数对方案排序影响的计算结果表13所示。

表13 基于ACMLGD的一致性水平阀与迭代循环次数对方案排序影响

从表13可知，不同一致性阀值δ水平条件，ACMLGD模型在大量产品评论的客户意见中发现客户总体偏好的计算结果。如果有高质量（一致性水一般平大于0.9，即δ≤0.1）及时间有限的客户总体偏好的计算需求，例如，在阀值的水平δ≤0.1条件，达到预定义一致性要求时，迭代次数仅为1200，因此，ACMLGD是低成本、快速地自动计算面向在线产品评论的大群客户偏好实用可行的方法。

4 结论

从广泛分布的评论文本、评分等级等大量信息碎片中计算大群客户总体偏好是非常耗时和昂贵的，目前有关客户偏好的相关研究文献尚未能提出有效方法解决如何在大量客户偏好的客户意见中低成本、快速地发现客户总体偏好。提出了一个通用的模型ACMLGD，用于低成本、快速地自动计算面向在线客户偏好的大群客户偏好。实验结果表明，ACMLGD模型在大量客户偏好的客户意见中发现客户总体偏好的计算性能较好。为在线客户偏好的大群客户偏好自动集结建模及应用提供了一种新的实用方法。进一步的研究工作将面向实际应用，把ACMLGD模型在大量客户偏好的客户意见中发现大群客户总体偏好计算方法应用于实际的ERP自动协同决策系统，支持企业相关战略及计划的决策。