一种改进的CLIQUE算法及其并行化实现

林鹏 ，陈曦 ，龙鹏飞 ，傅明

（1.长沙理工大学综合交通运输大数据智能处理湖南省重点实验室，湖南长沙410114；2.长沙理工大学计算机与通信工程学院，湖南长沙410114）

CLIQUE（Clustering In QUEst）[1]算法是一种典型的基于网格的聚类算法，具有聚类效率高，对数据输入顺序不敏感，可以随输入数据的大小线性的扩展等优点[2]。因此，CLIQUE算法经常被用于处理数据规模较大的数据集，也吸引了众多研究人员的关注。Sun Shaopeng等提出动态增量的方法改进了网格划分和剪枝算法[3]。王飞等将网格划分的思想代入密度峰值聚类，提出一种自适应分辨率的网格划分方法[4]。黄红伟等针对多密度数据集提出了一种Rn-近邻估计网格划分方法[5]。向柳明等在CLIQUE算法的基础上增加了采用高维随机采样的方法快速查找每个聚类簇中最密集的网格单元[6]。Lin JiaQin在文献[7]中提出采用高维分解技术和自适应网格的方法改善CLIQUE算法的局限性并提出了新算法在MapReduce[8]上的并行化实现方案。

针对CLIQUE算法采用固定宽度划分的缺陷，提出边界修正和滑动网格的方法对划分后的网格单元进行分析，填补聚类的边界，寻回被剪枝的稠密网格，提高聚类结果的准确性；然后结合Hadoop[9]和MapReduce实现了改进算法的分布式并行化并进行了相关实验。

1 CLIQUE算法的改进

1.1 问题描述

传统的CLIQUE算法在处理问题空间时，根据给定的划分参数将问题空间每一维等分为若干分，然后使用 MDL（Minimum Description Length）[10]算法对划分后的网格单元进行剪枝，剔除网格密度低于给定的密度阈值的网格单元。但是当给定的划分参数不恰当时，会导致算法忽略稠密区域的边界甚至整个稠密区域，使得聚类结果呈锯齿状或丢失聚类，降低聚类结果的准确性。图1（a）和图1（b）分别展示了采用固定宽度划分问题空间的缺陷。

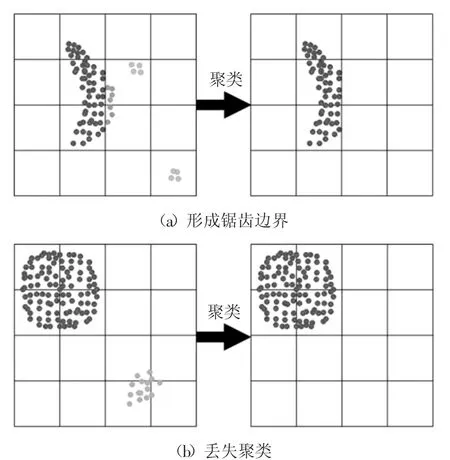
图1 采用固定宽度划分的缺陷

针对该缺陷提出边界修正方法和滑动网格方法，通过对划分后的网格单元进行分析处理，寻回丢失的稠密网格，从而提升算法的聚类效果。

1.2 边界修正方法

边界修正的基本思路是对聚类边界的稀疏网格单元做进一步划分，考察其子单元是否满足一定条件，将满足条件的子单元合并到相邻的稠密单元，补全聚类边界。该方法针对CLIQUE算法采用固定宽度划分的缺点，对所有位于聚类边界的稀疏网格单元进行处理，将它们等分为2n个子单元，统计每个子单元中数据点的数量，判断这些子单元的密度是否大于或等于给定的密度阈值且紧邻于某一个稠密单元，如果条件成立，则将子单元合并到邻近的稠密单元，否则不作处理。具体步骤如下：

（1）假设数据集 D={x1，x2，…，xn}的维数为d，网格u为边界稠密网格，考察其邻近网格单元是否存在稀疏网格单元u′，若存在则进行步骤（2），否则不作处理；

（2）对稀疏网格单元u′的每一维都做进一步二等划分，得到 2d个子单元 us={us1，us2，…，us2d，}；

（3）统计落入到子单元 usi|i=1，2，…，2d中的数据点的数量，判断条件 density（usi|i=1，2，…，2d）是否成立，若条件成立则进行步骤（4），否则不作处理；

（4）合并满足条件的子单元 usi|i=1，2，…，2d到稠密网格u，重复步骤（1）至（4），完成所有稀疏网格的处理。图2为在二维空间使用边界修正进行网格修正。

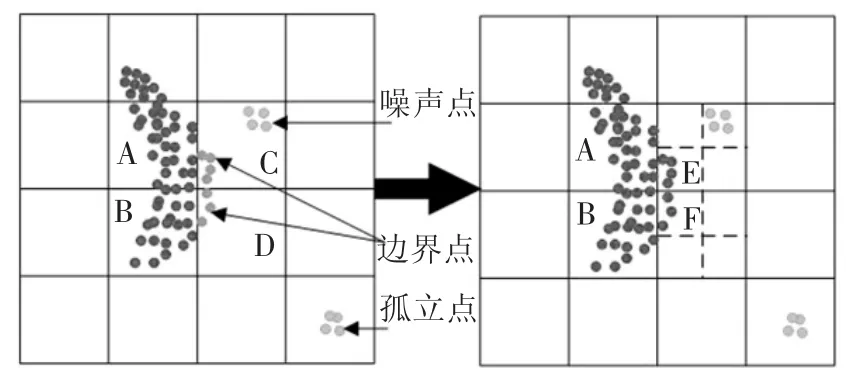
图2 采用边界修正处理低密度网格单元

1.3 滑动网格方法

滑动网格方法是对边界修正方法的一个补充，改进算法对稠密区域进行边界修正，仅仅确定了聚类的边界，而对于没有相邻稠密单元的低密度网格单元，其中的数据点会被作为孤立点处理，使得聚类的准确性降低。该方法采用滑动网格的思想，搜索没有邻近稠密网格的稀疏网格单元，对可以组成田字格的网格单元做进一步划分，将新划分的网格沿特定方向滑动，尽可能寻回稀疏区域的稠密网格。具体方法为计算各网格的矢量坐标以及网格滑动的方向矢量其中c为0田字格中所有网格的公共顶点，gi为网格ui的重心，计算公式如下：

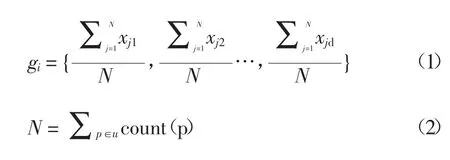
xj|j=1，2，…，N={xj1，xj1，…，xjd}为网格 u 中的数据点，N为网格中数据点的数量。以c0为中心重新划分网格，将新划分的网格沿着矢量方向滑动，统计落入新网格中数据点的数量，判断其密度是否大于或等于给定的密度阈值，若条件成立，则将新网格标记为稠密网格，否则不作处理。滑动网格方法的具体实现步骤如下：

（1）假设数据集的维数为d，SU={u1，u2，…，u2d}为没有邻近稠密网格的稀疏网格单元，计算各网格的重心点坐标 gi|i=1，2，…，2d；

（2）计算网格 ui|i=1，2，…，2d的矢量坐标，记为c0-gi，c0为SU={u1，u2，…，u2d}中网格的公共顶点，根据各网格的矢量坐标计算网格滑动的方向矢量

（3）c0以为中心点重新划分一个与原网格大小相同的网格u′，将网格u′沿着矢量的方向滑动，滑动距离为

（4）统计落入网格u′中数据点的数量，判断其是否满足 density（u′）≥ τ，若满足则将网格 u′标记为稠密网格，考察其余稀疏网格单元。图3为在二维空间中使用滑动网格方法进行网格修正。

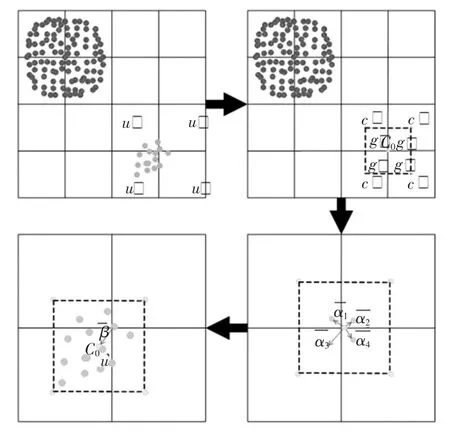
图3 采用滑动网格处理低密度网格单元

1.4 时间复杂度分析

改进算法与原算法相比，增加了网格修正的过程。在网格修正过程中，算法将扫描一次所有存在数据点的网格，然后稀疏网格中的数据点进行操作，因此该过程的时间复杂度为O（m×w×d），其中m为存在数据点的网格个数，w为每个稀疏网格中包含数据点的个数，在正常情况下，稀疏网格中包含的数据点的数量应远小于数据集中所有数据点的数量，因此m×w≤n。在CLIQUE算法中，采用自底向上的方法进行聚类，算法的时间复杂度为O（nd+cd），c是一个常数。在本文算法中，增加了网格修正的过程，因此时间复杂度为O（n′d+cd），其中n′=n+m×w，又因为m×w≤n，所以 n′≈n。

1.5 改进算法的聚类效果分析

本文分别测试了CLIQUE算法、文献[10]中的GP-CLIQUE算法和本文算法对不同大小、不同形状的二维数据进行聚类的聚类效果。使用二维数据进行实验可以更直观的看到聚类结果，也便于比较不同算法的聚类效果。图4为使用三种算法对同一个数据集进行聚类的效果对比图。

图4 算法聚类效果对比图

从图4可以看出，对于该数据集，使用CLIQUE算法聚类时，外部圆环部分缺失大量边界，圆心部分被聚类成两个不同的类，虽然GPCLIQUE算法的聚类质量有所提升，但效果也不理想，使用改进算法聚类时，成功找回外部圆环的边界和圆心，聚类效果明显。因此，使用本文提出的方法改进CLIQUE算法，能够有效的提高聚类结果的准确率。

图5为使用3种算法对4个不同形状不同规模的数据集进行聚类的准确率比较，可以明显看出改进后算法的聚类准确率保持在90%以上，聚类效果明显优于GP-CLIQUE算法和CLIQUE算法。这是因为使用本文方法对划分后的网格进行处理后，寻回了丢失的稠密区域，提高了聚类质量。而GPCLIQUE算法的准确率比CLIQUE算法略有提高，这是因为虽然GP-CLIQUE算法采用高斯随机采样的方法提升了聚类性能，但还是采用固定宽度划分方法，所以算法性能的提升低于本文算法。准确率计算公式为：Accuracy=ncorrect/n。

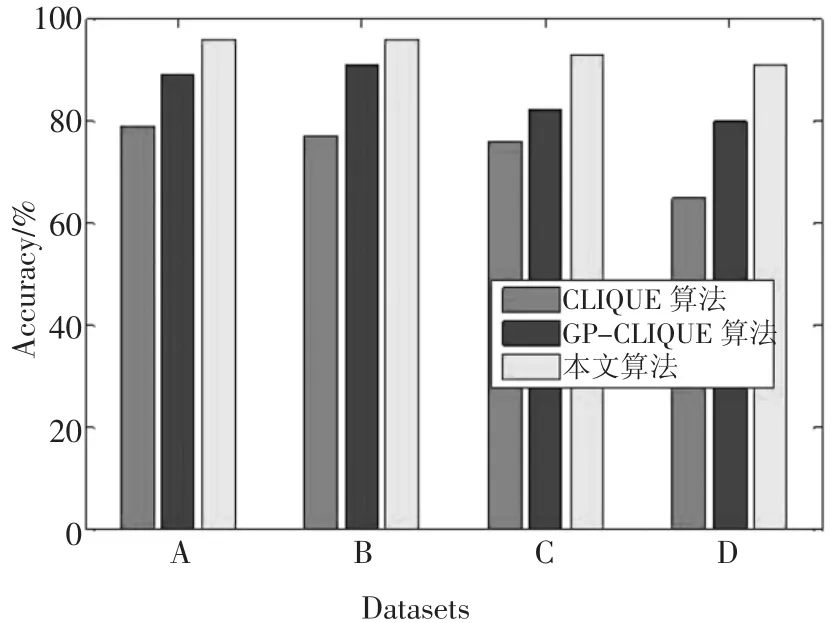
图5 聚类准确率比较

2 改进算法的并行化实现

改进的CLIQUE算法并行化的思想：将算法的并行化分为网格划分和聚类两个阶段，在每个阶段启动1个Job完成网格划分和聚类操作。图6为改进算法的并行化实现流程图。

初始阶段。对数据集进行预处理操作，由Job－Client把数据集切片为的形式并发送到JobTracker，Job1启动时从InputSplit中加载切片信息作为Map函数的输入。

Job 1网格划分阶段。Job1的主要任务为对问题空间进行网格划分，然后采用改进算法提升网格划分质量，最后输出划分结果。其中每次计算都需要调用多个Map和Reduce函数，Map函数负责计算数据点所属网格的编号，将网格的编号和其中包含的数据点作为中间值输出；Reduce函数负责汇集各个网格中的数据点并计算各网格的网格密度，将网格密度与给定的密度阈值进行比较，若大于密度阈值则将网格标记为稠密网格，否则使用第2章所述方法进行调整，最后输出最终的网格划分结果。

Job 2聚类阶段。Job2的主要任务为遍历Job1生成的稠密网格，以深度优先的方法搜索连通的最大单元簇，输出聚类结果。Map函数以Job1的输出作为输入，从中解析出网格编号和各网格包含的数据点，创建一个哈希表Cells用于存储网格信息并初始化，哈希表的key即为网格编号，value为网格中包含的信息，包括网格中包含的数据点，网格所属类簇编号和网格的状态信息；Reduce函数接收Map函数输出的中间值，随机选取一个网格，检索其连通的所有网格并更新哈希表中这些网格的所属类簇和状态信息，选取下一个尚未聚类的网格进行聚类，直到所有网格都属于某个类簇或所有网格的状态信息均为已读。

3 实验与结果分析

3.1 实验环境和数据

本文实验环境为Linux操作系统，搭建了一主四从的小型分布式集群，各节点虚拟机处理器配置为Intel Xeon CPU E5-2650 v2，内存 4GB，软件为Hadoop-2.6.0版本。实验数据采用从UCI机器学习库中选取的美国1990年的人口普查数据，该数据集的维度为68，共有2458285条数据，通过人工处理，将数据集抽样为6个大小不同的数据集，使得每个数据集的数据量以接近2倍大小的速度增长。

3.2 实验结果与分析

3.2.1 算法时间效率分析

为确保实验的准确性，每组实验都重复进行5次，最终的实验结果取5次实验的平均时间。由表1的结果可以看出，当数据量较小时，串行算法的处理效率要比算法在MapReduce运行的效率高。这是由于在MapReduce并行框架下运行程序会启动一个新的Job，新Job的启动和交互过程中会增加时间消耗。但是随着数据量的逐渐增加，串行算法的性能会随之下降，最终抛出内存不足的异常，而并行算法的效率随着数据量的增加逐渐优于串行算法，因此在处理海量数据时，有必要采用分布式集群模式。

为测试算法的并行效率，分别选择1，2，3，4个计算节点处理数据，考察在增加节点的情况下，集群运行算法需要的时间。如表1所示，在数据规模较小的情况下，增加计算节点，对算法运行加速效果不明显。如对于数据集USCensus-1，随着计算节点的增加，算法的处理时间在1190s上下浮动，这是由于Hadoop集群启动和调用计算节点需要花费时间；而当数据规模变大时，随着计算节点数量的增加，算法处理数据所消耗的时间也随之减少，且数据量越大加速效果越明显。由此可见，当数据规模较大时，增加处理节点可以显著提高算法对相同规模的数据集的计算能力，同时体现了改进算法具有良好的扩展性。

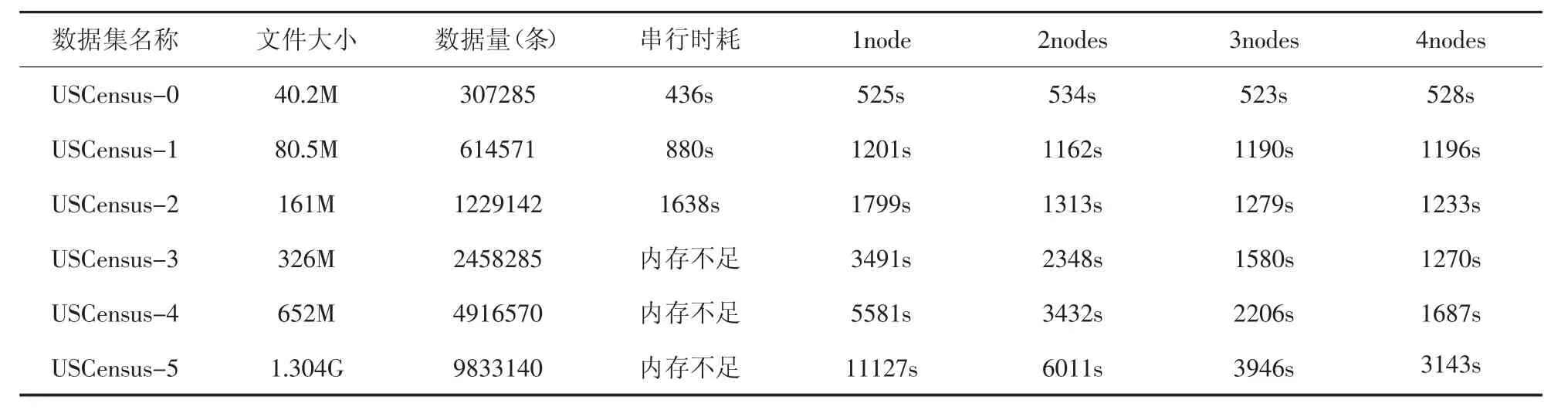
表1 算法处理时间

3.2.2 集群加速比性能实验

实验1加速比是衡量算法串行处理和并行处理效率的一项重要指标，本文计算了处理表1中不同大小数据集的加速比，实验使用单个节点的Hadoop集群即一个主节点和一个从节点的情况代替算法串行处理时间的近似值。由图7的结果可以看出，随着数据规模的逐渐扩大，算法的加速比性能越来越好。

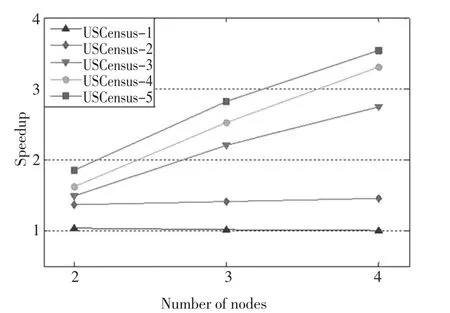
图7 加速比分析

实验2并行算法的可扩展率是评价算法并行计算效率的重要指标之一，可以有效反映集群的利用率情况，随着计算节点数的增加，若算法的可扩展率保持在1.0附近或者更低，则表示算法对数据集的大小具有很好的适应性。从图8中可以看出，算法的可扩展率曲线一直保持在1.0以下，且随着计算节点数的增加可扩展率曲线总体呈下降趋势，当数据集越大时，可扩展率曲线就越平稳，因此可以得出，数据集规模越大，算法的可扩展率性能就越好。

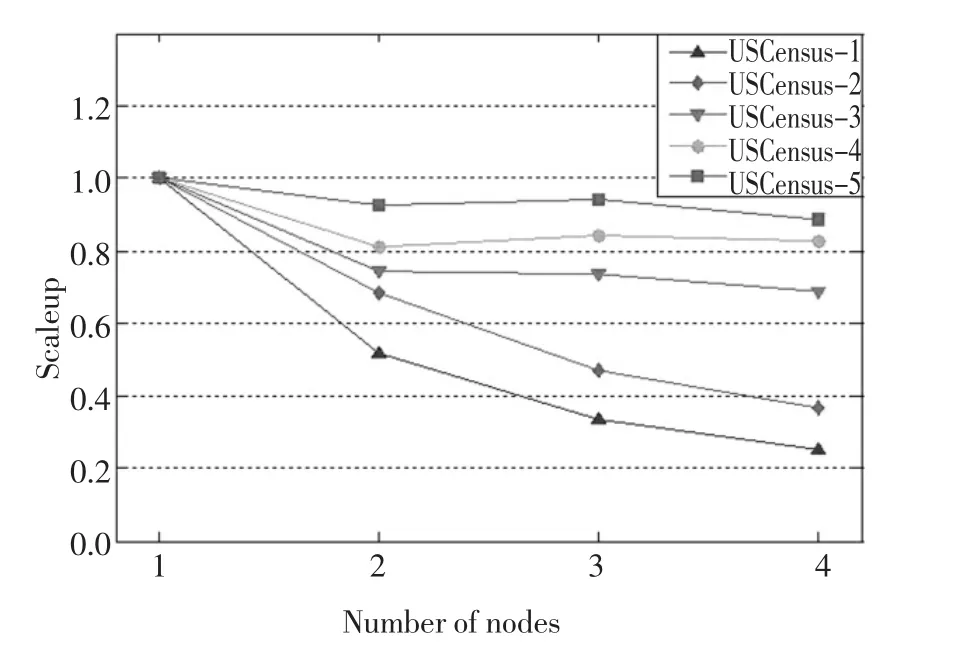
图8 可扩展性分析

4 结束语

提出了一种改进的CLIQUE算法，根据给定的划分参数对数据空间进行划分，然后提出边界修正方法和滑动网格方法对划分后的网格进行处理，提升网格划分的质量；同时在Hadoop分布式平台上，利用MapReduce实现了改进后算法的并行化。文中使用人工生成的数据集和UCI数据集对改进算法进行了一系列实验，测试了算法的聚类精度、时间效率、加速比、数据伸缩率和可扩展性。实验结果表明，使用本文方法改进CLIQUE聚类算法并在MapReduce上实现并行化，使得聚类结果的准确率提升了17%～26%，同时也表现出良好的数据伸缩率和可扩展性，算法具有处理海量数据的能力。下一步将着力于解决CLIQUE算法依赖密度阈值与划分参数的输入的问题。