一种火箭发射场坪流场的环形线汇描述方法

谢 建，权 辉，谢 政

(火箭军工程大学兵器发射理论与技术军队重点实验室，西安 710025)

0 引 言

火箭发射时，发射场坪上的流场发生剧烈变化[1]，会对设施设备产生巨大影响：一是发射过程中燃气流对场坪上的建筑设施及设备产生冲击；二是场坪上的小型设备、颗粒杂物等被气流卷吸进入发射井，对火箭及井内设施设备产生危害。所以，发射场坪上流场的流动规律是值得重点关注的问题之一。

对于火箭发射时的流场，王飞采用流体计算软件对W型地下井发射过程进行了数值模拟，分析了压力和温度的变化规律[1]。李军采用数值模拟方法研究了固体火箭燃气流场形成和发展的机理[2]。马溢清采用气液两相流模型对火箭发动机尾焰注水降噪效果进行了研究并做了缩比试验[3]。傅德彬应用动网格技术对火箭发射过程中的燃气流场进行了数值模拟，分析了燃气流场对火箭气动力的影响[4-5]。姜毅采用一维等熵流方法和有限体积法分析了固体火箭发动机尾焰流场的流场结构和燃气组分分布[6-7]。杨宏伟对火箭垂直发射时的流场进行了数值模拟，得到了流场变化规律[8]。谢政等采用数值方法研究燃气流的二次燃烧现象以及点火压力脉冲形成机理和影响因子[9-10]。单时卓采用数值方法对舰载导弹垂直发射过程中的燃气流场进行了分析[11]。周笑飞对井下发射燃气射流的数值模拟方法进行了深入研究[12]。这些研究多数针对某一具体问题进行研究，其结果对于后续相关研究具有重要指导意义。

随着火箭技术的不断进步和火箭运用方式的不断发展，发射场坪流场的研究变得尤为迫切，必须进行深入分析，建立一套行之有效的分析方法。本文基于势流法提出环形线汇模型对发射场坪上的流场进行描述，分析发射场坪流场的速度变化规律，并与FLUENT仿真结果进行对比，验证方法的可行性，为后续发射井相关问题的研究提供新的思路。

1 环形线汇方法

1.1 工程背景介绍

某型火箭发射井构型如图1所示，火箭由发射台支撑竖立在发射井中，点火后燃气尾焰由排焰道排除井外，火箭在燃气射流的反作用推力下起飞出井。从火箭点火到出井过程中，发射场区的流场经历爆震波阶段、引流阶段和失稳阶段等三个明显的阶段变化[1][9]。

在引流阶段，火箭燃气射流在井下狭窄空间内产生引射作用，整个发射井相当于大型的引射器，在引射器作用下发射场坪上形成强烈的引流流场。引流流场中流体介质主要为场坪上的空气，温度为常温，流动过程中流速低于声速，相对于高温高速燃气射流，可以作为不可压缩流体进行处理。由于空气边界层很薄，而边界层外流体黏性作用可以忽略[13]，为简化分析，本文采用理想流体进行计算。

为方便研究，对发射场坪流场进行适当简化。如图2和图3所示，将火箭与井壁间隙(以下简称箭井间隙，并用d表示)简化为环形线汇，半径取为火箭半径与发射井半径的平均值，于是发射井出口处的流场可以用环形线汇流场来描述。

1.2 环形线汇流场速度势推导

设环形线汇强度为Q1，半径为R，如图3所示，以发射场坪中心为原点，场坪所在平面为XOY平面，沿发射井轴向指向火箭头部方向为Z轴正向，建立右手O-XYZ笛卡尔坐标系，场坪上空中一点M(x,y,z)受到井口一点N1(Rcosθ,Rsinθ, 0)作用的速度势[14]为

(1)

沿井口圆环对φ1积分可得M1受到整个环形线汇作用的速度势为

(2)

式中：γ为OM1在XOY平面的投影线OM1＇与X轴正向夹角。

(3)

式中：K(ζ)为第一类椭圆积分[15-16]，ζ为模数。

设井壁与火箭间隙流场为均匀流动，速度为v，则Q1可以表示为

(4)

于是m1式可以化为

m1=v(R2-R1)

(5)

令d=R2-R1，将(5)式代入(3)式可得

(6)

1.3 环形线汇流场速度的推导

根据势流理论

(7)

式中：u1、v1、w1分别代表发射场坪X、Y、Z三个方向的流速(X、Y、Z方向如图3所示)。

将(6)式代入(7)式，结合第一类椭圆积分的求导公式[18]可得

(8)

式中：E(ζ)为第二类椭圆积分，ζ为其模数。

同理可得

(9)

(10)

1.4 环形线汇流场理论计算

根据公式(8)(9)(10)，取v=-100，d=0.5，y=0，R=1.55，z=0.1，x∈(-12, 12)得到X方向速度vx如图4所示。从图上可以看出，发射场坪地面附近水平速度在靠近井口时急剧增大，且在井口半径以内沿半径增大方向，在井口半径以外沿半径减小方向，这显示出流体向井的环形出口处聚集。

取v=-100，d=0.5，y=0，x=R=1.55，z∈(0.1, 12)得到Z方向速度vz如图5所示。从图上可以看出，在箭井间隙附近流体竖直方向速度沿Z轴负向急剧增大，随着高度增加，速度逐渐趋近于0。

由ζ表达式可知，环形线汇模型的奇点位置为场坪地面上半径为R的圆，在流场奇点附近速度趋近于∞，与实际流场有很大差距，在图4、图5上可以直观看到这一现象，所以奇点附近的取值不宜作为实际流场的估算数据。

2 FLUENT仿真模型的建立

2.1 计算模型

本文以FLUENT仿真结果对比分析势流理论计算结果的偏差。为简化分析计算，采用圆柱轴对称模型，选取的几何模型如图6所示，轴对称处理的平面模型如图7所示。为估计火箭半径(r)以及箭井间隙(d)大小对环形线汇模拟发射场坪流场的准确度的影响，r值分别取为1.0 m、1.5 m、2.0 m、2.5 m、3.0 m，d值分别取为0.1 m、0.3 m、0.5 m、0.7 m、0.9 m，建立相应的几何模型。为几何模型划分四边形网格，以r=1.0 m，d=0.5 m为例得到的网格模型如图8所示。

边界条件和监测线的设置如图7所示。在软件界面中选择圆柱轴对称、稳态模型，k-ε湍流模式[17]，以常温常压全局初始化，入口速度v分别选择-60 m/s、-100 m/s、-200 m/s、-300 m/s进行计算，得到监测线上的速度数据。

2.2 网格无关性验证

在使用大型仿真软件进行流场计算中，先将流场区域划分成微小有限体积，再将控制微分方程组离散化为差分方程组，使用迭代方法求解，在此过程中会产生截断误差和舍入误差，截断误差随着网格划分的加密逐渐缩小，而舍入误差会随着计算迭代次数的增多而增大。在实际计算机仿真中，计算结果的精度会随着网格密度的增加而提高，而且提高量会相对越来越小，但是所需要的计算资源却会急剧增加。为使用有限的计算资源达到可靠的计算精度，需要进行网格无关性验证，即确定最小的网格数以取得所要求的计算精度。

本文中以r=1.0 m，d=0.5 m时几何模型进行网格无关性验证，得到适用于本项研究的网格密度。分别对网格数为19641、31376、42455、56204的四套网格进行计算，得到径向监测线上的速度幅值如图9所示。从图上可以看出，网格数为19641的网格模型其监测线上速度幅值的计算结果与其他三种网格模型差距明显，最大值为88.4347，而其余三种分别为81.2527、81.5286、82.6366。为保证计算精度，同时有效减少计算量，本文选取网格数为31376的网格模型的网格密度作为网格划分的方案。

3 理论计算结果与仿真结果的对比

皮尔逊相关系数[18]广泛用于度量两个变量之间的线性相关程度，其值介于1和-1之间，趋近于1表明正向线性相关性趋强，趋近于-1表明负向线性相关趋强，趋近于0表明线性相关性趋弱。本文中用两种方法计算同一个物理量——速度，数据结果之间没有明显平移和比例差距(见图10～12)，所以仅用相关系数表明两种结果的接近程度。

3.1 不同速度入口条件下环形线汇模型与仿真结果的差异

取火箭半径r=1.0 m，分别取d=0.1 m、0.3 m，将入口速度v分别设为-60 m/s、-100 m/s、-200 m/s、-300 m/s，得到软件仿真结果。分别提取径向监测线上的径向速度数据和轴向监测线上的轴向速度数据与环形线汇理论计算结果进行对比，计算两种方法得到曲线的相关系数如表1和表2所示，表中ρr表示径向速度相关系数，ρa表示轴向速度相关系数。从表中可以看出，d=0.1 m时，理论计算结果与软件仿真结果吻合得非常好；d=0.3 m时，理论计算结果与软件仿真结果的差距增大；不同入口速度对理论计算和软件仿真结果的相关系数没有显著影响。

为直观地比较两种方法计算结果的差距，取d=0.3 m时两种方法得到的径向监测线上径向速度数据画出曲线如图10所示，图中水平坐标轴是径向监测线上位置，单位是m，纵坐标是径向速度，单位是m/s，实线是FLUENT仿真结果，虚线是公式计算结果。从图上可以看出，虽然速度绝对值变大，但是两种方法得到的曲线差值变化趋势基本一致。

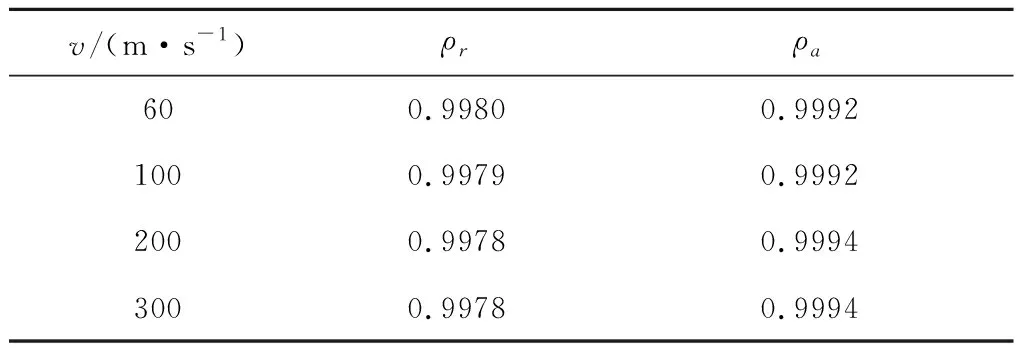
表1 d=0.1 m时不同入口速度条件下两种方法计算结果的相关系数Table 1 Correlations of the results from the two methods under different inlet velocities when d=0.1 m

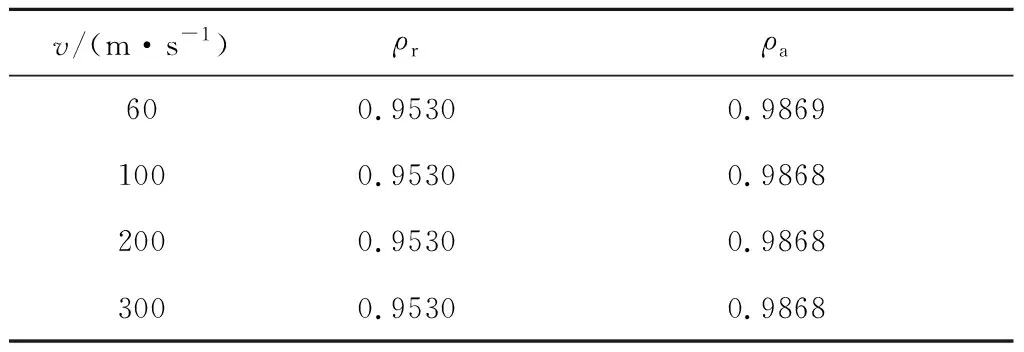
表2 d=0.3 m时不同入口速度条件下两种方法计算结果的相关系数Table 2 Correlations of the results from the two methods under different inlet velocities when d=0.3 m

3.2 不同r值、d值条件下环形线汇模型计算结果与仿真结果的差异

取入口速度v为-100 m/s，用软件计算不同r值、d值的流场模型得到25组计算结果。从计算结果中分别提取轴向监测线上的轴向速度数据(记为vaa)，计算其与环形线汇理论计算结果的相关系数如表3所示，分别提取径向监测线上的径向速度数据(记为vrr)，计算其与环形线汇理论计算结果的相关系数如表4所示，表中ρ0.1、ρ0.3、ρ0.5、ρ0.7、ρ0.9分别表示d=0.1 m、0.3 m、0.5 m、0.7 m、0.9 m时的相关系数。从表中数据可以看出：r值的变化对两种方法计算结果的相关系数没有显著影响；轴向监测线上的轴向速度数据的相关性明显好于径向；d=0.1 m时，理论计算结果和软件仿真结果符合得较好；随着d值的增大，理论计算与仿真结果的差距逐渐增大。

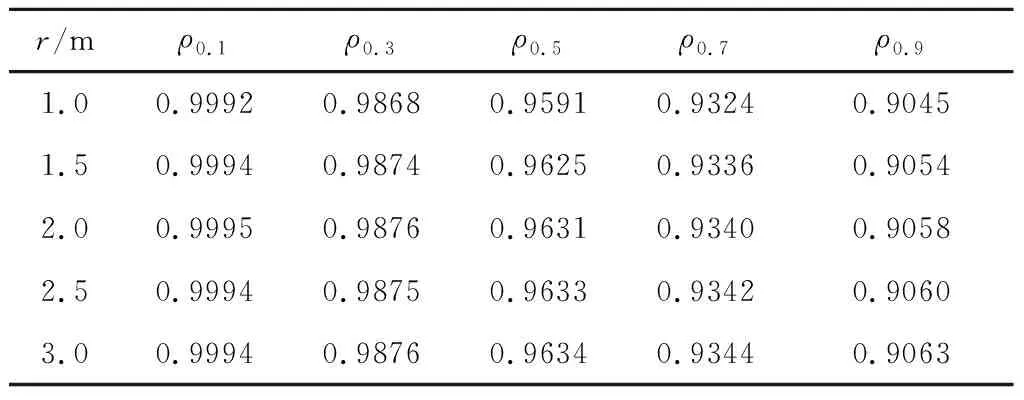
表3 两种方法计算得到的“vaa”的相关系数Table 3 Correlations of “vaa” from the two methods

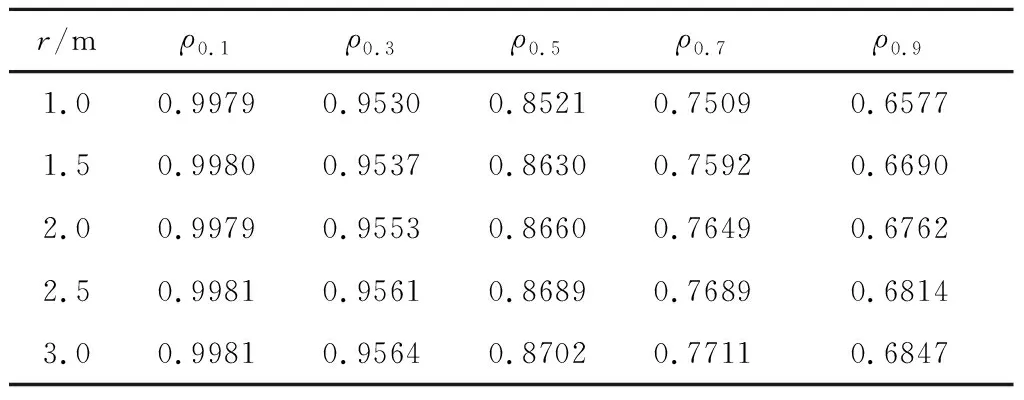
表4 两种方法计算得到的“vrr”的相关系数Table 4 Correlations of “vrr” from the two methods

为了直观地比较两种方法计算结果的差距，取d=0.5 m时不同r值下两种方法得到的径向监测线上径向速度数据画出曲线如图11所示(图例意义同图10)，取r=1.0 m时不同d值下两种方法得到的径向监测线上径向速度数据画出曲线如图12所示(图例意义同图10)。从图11可以看出，理论计算值随着r值增大而减小，但是两种方法得到的曲线差值变化趋势基本一致。从图12可以看出，随着d值增大，速度绝对值增大，同时两种曲线差距也越来越大。

4 结 论

本文采用势流法对发射场坪上的流场进行研究，推导了环形线汇流场速度势和速度的计算公式，在FLUENT软件中建立发射场坪流场计算模型并进行求解，在不同r值、d值和不同速度入口条件下分别对环形线汇与软件仿真两种方法流场计算结果的差异进行了分析，得到了以下结论：

(1)不同火箭半径和流场引流入口速度对理论计算和软件仿真结果的误差没有显著影响；

(2)两种方法得到的轴向监测线上轴向速度数据的相关性明显好于径向监测线上的径向速度；

(3)环形线汇模型在d值较小时与软件仿真得到的流场速度较为一致，随着d值得增大，两种方法得到的流场速度差距逐渐增大，当d>0.5 m时，径向监测线上的径向速度数据相关系数在85%以下；

(4)环形线汇模型能够反映发射场坪流场速度的变化趋势，在d值较小且误差允许时可以作为发射场坪流场的简化描述。