The energy-saving advantages of burst-and-glide mode for thunniform swimming *
Dan Xia (夏丹), Wei-shan Chen (陈维山), Jun-kao Liu (刘军考), Xiang Luo (罗翔)
1. School of Mechanical Engineering, Southeast University, Nanjing 211189, China
2. State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150001, China
Abstract: This paper explores the energy-saving advantages of the burst-and-glide swimming and compares it with the normal self-swimming for a thunniform swimmer. The virtual swimmer allows us to perform controlled numerical experiments by varying the swinging tail number and the duty cycle while keeping the other parameters fixed. 3-D Navier-Stokes equations are used to compute the viscous flow over the swimmer. The user-defined functions and the dynamic mesh technology are used to simulate the burst-and-glide swimming. The results show that with the increase of the swinging tail number or the duty cycle, the swimming velocity, the power and the efficiency all increase, but the velocity-power ratio decreases somewhat. Therefore, choosing smaller swinging tail number and duty cycle is beneficial in reducing the power and increasing the velocity-power ratio, and thus to obtain the same velocity, less power is consumed. And to swim the same distance, the energy can significantly be saved. The power consumption,the efficiency and the velocity-power ratio in the burst-and-glide case are 43.9%, 40.6% and 1.15 times of those in the normal swimming case, respectively. The flow structures clearly show the evolution process around the fish in the burst-and-glide swimming.The findings can be used to reasonably plan the swimming action and to take the advantage of the external flow field energy for the fishlike robot, to be more efficient and energy-saving.
Key words: Energy-saving advantages, burst-and-glide mode, normal self-swimming, thunniform swimmer
Introduction
The burst-and-glide swimming mode is widely adopted by a variety of biological fish and marine animals, such as tunas, dolphins, whales and other underwater aquatics[1]. This kind of swimming mode consists of a burst motion within several circles and a glide motion in a single phase. During the glide motion, the fish body remains in a straight line posture without action[2-3]. For biological fish, the energysaving advantage is undoubtedly the main reason for its adoption of the burst-and-glide swimming. It is generally believed that this way is also energyefficient and can produce a high mobility, but without any accurate data to prove[3-7]. The researches of the burst-and-glide swimming are relatively few.
Ribak et al.[4]noted that for achieving the same velocity, it was inferred from a comparison model of active and passive resistances that the burst-and-glide mode can save more energy than the normal cruise.Fish and Murray[5]considered that the individual in the wake region of fish schooling often adopted the burst-and-glide mode to keep itself in the position of the cluster of fish. Yang et al.[6], Chueng[7]studied the fluid forces and the flow structures of the burstand-glide swimming for a two dimensional subcarangiform fish. Muller et al.[8]tested and quantitatively described the burst-and-glide swimming of the juvenile and adult zebrafish and noted that the burst-and-glide swimming is rarely seen in the flow of low Reynolds number. Wu et al.[9]measured the kinematic features and the wake pattern of the burstand-glide swimming of koi and proposed two burst-and-glide modes: MT (multiple-tail-beat) mode and HT (half-tail-beat) mode. However, for the thunniform fish, their burst-and-glide swimming has not been much studied.
Numerous recent experiments by using the particle image velocimetry techniques[10-13]provided a wealth of data in terms of both swimming kinematics and wake structures. However, controlled experiments for various kinematic behaviors of a live fish are difficult to perform. This shows that the experimental method alone can not provide conclusive findings for the burst-and-glide swimming of the thunniform fish.However, some insights can be obtained by combining experiments with numerical simulation approaches[14-15]. So far, numerical studies of fish swimming are relatively few. Perhaps the most comprehensive numerical studies are by Bottom et al.[16], Zhu and Shoele[17], who used an inviscid model to study the wake structures of a straight-swimming giant danio.Borazjani and Sotirpoulos[18]carried out the self-propelled simulations to study the hydrodynamics and the wake structures of the swimming of carangiform and anguilliform. These studies shed new light into the mechanisms of aquatic swimming. However, they focused on simulating a specific aspect of aquatic swimming, and systematic parametric investigations of the mechanism of the burst-and-glide swimming are highly desirable.
This paper will explore the energy-saving advantage and the mechanism of the burst-and-glide swimming for the thunniform fish. The implicit coupling method is adopted to solve the swimming kinematics and energetics of the burst-and-glide swimming with fluid-structure interactions. By comparing with the normal self-swimming, the energysaving advantages of the burst-and-glide swimming are revealed. In the development process of a fishlike robot, a better knowledge of the mechanism of the burst-and-glide swimming can help to reasonably plan the swimming action and take the advantage of the external flow field energy, to be efficient and energy-saving.
1. Physical model and kinematics
1.1 Physical model
In this work, we employ a small tuna model as the virtual swimmer, composed of a main body with a smooth profile and a high-aspect-ratio caudal fin,neglecting all other minor fins. The physical model is identical to that used in our previous work on the thunniform swimming[15]. The size of the swimmer xyz×× is set to 0.20 m×0.03 m×0.06 m. We establish the coordinate system of the fish bodyand that of the caudal finshown in Fig. 1.
The origin of Obxbybzbis located at the swimmer head, and that of Ocfxcfycfzcfis located at the caud al peduncle, at the p lace 0.85 times the swimmerlengthmeasuredfromthehead.Duringthe swimming process, the swimmer is assumed to start from rest to self-propelled steady state swimming when the mean axial force on the fish is zero.
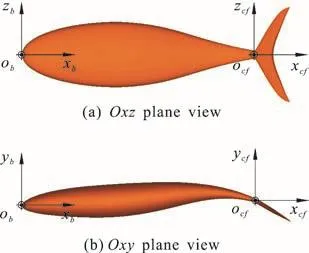
Fig. 1 (Color online) Physical model of thunniform swimmer
1.2 Kinematics
The kinematics of the burst-and-glide mode involves two phases of “burst” and “glide”. In the“burst” phase, the swimmer swings its body and in the“glide” phase, it stretches the body to a straight line.In terms of kinematics, these two actions of swinging and stretching body are a continuous process. While establishing the kinematic model, in the “burst” phase,we, respectively, set a “start” stage and a “slow” stage.The swinging amplitude of the former gradually increases from 0, that of the latter is gradually reduced to 0 and in the intermediate stage, the amplitude is constant. Therefore, the kinematics of the burst-andglide swimming can be subdivided into four stages of“start-swing in constant amplitude-slow-glide”, the first three stages are in the burst phase and the fourth is in the glide phase.
In order to properly describe these four stages of the burst-and-glide swimming under the self-propulsion, a start-stop termis introduced to control the kinematics of the four stages. The body kinematics with consideration ofcan be described as

where yb-c(x, t) is the instant lateral displacement,A( x) is the amplitude function, ω is the wave frequency, k is the wave number, denoted as k=2π/λ, and λ is the wave length.
Figure 2 shows the time history of the caudal peduncle’s lateral displacement yb-c(0.85,t) within two burst-and-glide circles when the start-stop item ab-c(t) is introduced. ab-c(t) can be described as:

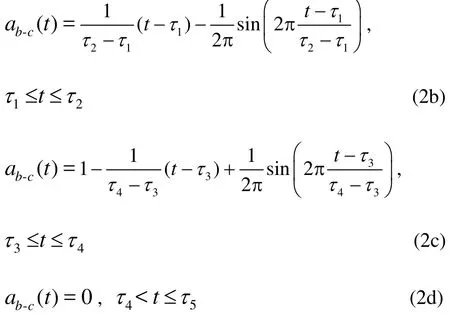

Fig. 2 Time history of -()b c ta
During the burst-and-glide swimming process,the caudal fin kinematics is the same as that of the normal swimming under the self-propulsion as discussed in our previous work on the thunniform swimming[15], where more details can be found. What is different is the start-stop items[7,19]. The caudal fin kinematics can be described as
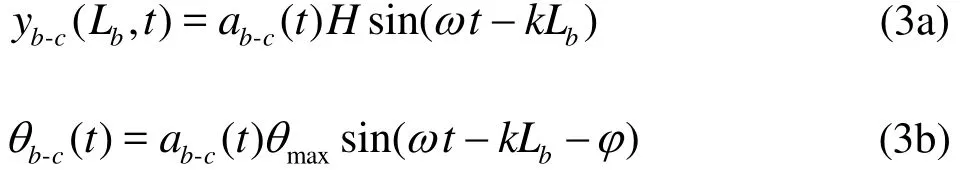
With the help of Fig. 2, several important parameters of the burst-and-glide swimming are defined:(1) the cycle of the burst-and-glide swimming-bcT, wherebT is the burst cycle andcT is the glide cycle. (2) the duty cyclewhich represents the percentage of the burst cycle in the entire burst-and-glide cycle. When =0D , it is in the pure glide state, when =1D , it is in the pure burst state, namely, as in the normal self-swimming,when 0< <1D , it is in the burst-and-glide state. (3)the continuous swinging tail number n in the burst phase, which in Fig. 2 is 2. If D and n are given,we can uniquely determine the kinematics of the burst-and-glide swimming.
To further study the energy-saving mechanism of the burst-and-glide mode and compare it with the normal swimming[15], in this work, we choose =λ
=0.075and φ=70°, and discuss the energy-saving advantages of the burstand-glide mode by varying the duty cycle D and the swinging tail number n.
2. Numerical method
2.1 Governing equations
The effect of the burst-and-glide mode on the energy-saving mechanism for the thunniform fish is studied in this paper. We consider a 3-D incompressible flow over the fish in the burst-and-glide swimming. The equations governing the motion of the viscous fluid are the 3-D Navier-Stokes equations given by:

where u is the fluid velocity vector, ρ is the density, p is the pressure, μ is the dynamic viscosity and ∇ is the gradient operator. To solve the equations in a domain containing the fish, a no-slip condition is needed to be imposed on the moving interface with the fluid velocity ζ˙ and the fish velocity x˙ as

In this work, the motion of the fish is in turn described by the Newton’s equations of motion as:

where F andZM are the fluid force and the torque acting on the fish, m is the fish mass,cx˙˙ is the swimming acceleration,cφ˙ andcφ˙˙ are the angular velocity and the angular acceleration, andZI is the inertial moment with respect to the yaw axis. The feedback of the torque is limited in the yaw direction to simplify the computations. The fluid force F and the torqueZM are as follows:

2.2 Numerical method and validation
The Navier-Stokes equations are discretized using a finite volume method: a second-order Crank-Nicolson scheme is used for the unsteady term, a second-order upwind scheme is adopted for the convective term and a second-order central differencing scheme is used for the diffusion term. The pressure velocity couplings of the continuity equation are dealt with by using the SIMPLE algorithm. The solution of the Newton’s motion equations for the fish is implemented by using a user-defined function. The coupling procedures are implemented using an improved staggered integration algorithm[15,20]. The mesh grids are locally refined near the fish and the wake region. To capture the movement of the fish in the 3-D domain, the dynamic mesh technique is used. At each updated time instant, the grids around the fish are regenerated and smoothed using the regridding and smoothing methods. The tail beat period T is divided into 200 time steps, i.e.To ensure the grid quality updated at each time step, a small time step size is used depending on the tail beat period.
The numerical method is identical to that used in our previous work on the thunniform swimming[15],where more details can be found in Refs. [15, 21]. The numerical method is validated extensively for the flows with moving boundaries and is applied successfully to simulate the fishlike swimming[15,21].
2.3 Swimming performance parameters
Several parameters are used to quantify the burstand-glide swimming performance. The component of the instant fluid force along the x direction (denoted ascan be computed by integrating the pressure and viscous forces on the fish as


The power loss due to the burst motion of the swimmer is calculated as

If the Froude efficiency η is defined based on the total fluid force, it is zero for the steady swimming[22]. Therefore, it is useful to define the Froude efficiency based on the thrust and the power loss as follows

For the swimming velocity, the component of the instant swimming velocity along the x direction can be non-dimensionalized as

For the acting force, the component of the instant fluid forceand the thrust) can be non-dimensionalized. Furthermore, the power loss due to the burst motion for the swimmer can also be non-dimensionalized as:

whereDC,DPC are the dimensionless fluid force and thrust, andPLC is the dimensionless power.
3. Results and discussions
3.1 Time history of velocity and force
The burst-and-glide swimming under the selfpropulsion is a kinetic process that the swimmer starts from a quiescent state, then gradually accelerates and eventually reaches the steady state in accordance with the burst-and-glide kinematics. The normal selfswimming was studied in our previous work for the thunniform swimmer[15]. In this work, we focus on comparing the kinematics and the energetics between the burst-and-glide mode and the normal self-swimming. Figure 3 shows the time history of the swimming velocity and the displacement in the burst-andglide mode and in the normal self-swimming when the swinging tail number =2n and the duty cycle D = 0.5. The time history of other parameters are similar.

Fig. 3 Time history of swimming velocity and displacement(N-S: normal self-swimming, B-G: burst-and-glide)
It is observed from Fig. 3 that when n = 2,D = 0.5, the swimming velocity in the burst-andglide mode is about 0.5 times of that in the normal self-swimming and the convergence process of the former is slower than the latter. During the process of reaching the steady state, the velocity fluctuation of the former is much more vigorous than that of the latter. This is because those four stages of “start-swing in constant amplitude-slow-glide” in the burst-andglide mode have alternating kinematics variations, and the velocity fluctuations within each cycle evidently include burst and glide phases. Through the comparison of the displacement curves of both swimming modes, we know that after reaching the steady state,the displacement in the burst-and-glide mode is about 0.53 times of that in the normal swimming. Since the velocity increases from zero during the process of reaching the steady state, and after several cycles of fluctuations, the steady state is reached. Therefore, as the time progresses, the swimming displacement increases slowly at first and then gradually increases in a linear manner.
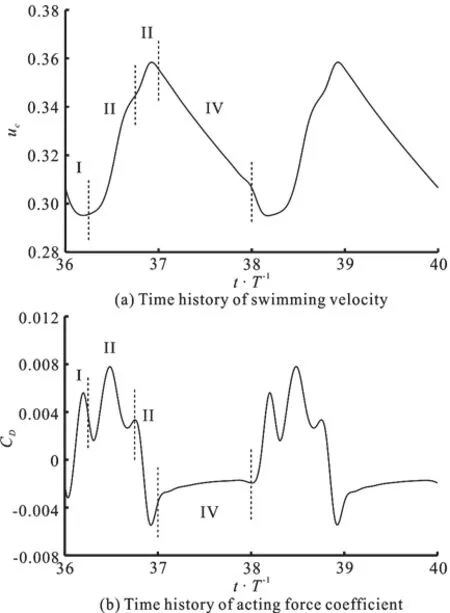
Fig. 4 Time histories of velocity and force during steady swimming
After reaching the steady state, the velocity and the acting force in the swimming direction are periodically changing but not in a sinusoidal manner,which can be understood as follows: during the burstand-glide swimming process, as four stages have alternating kinematics, the velocity and the force also show periodic changes. Figure 4 shows the variations of the velocity and the force in two cycles. From Fig.4, the following findings can be obtained.

Fig. 5 (Color online) The vorticity contours (VC) of burst-and-glide and normal self-propulsion
(1) When =2n , =0.5D , the cycle of the burst-and-glide mode-bcT is twice of the burst cycle Tb. The curve of the swimming velocity ucwithin a cycle-bcT includes four regions of I, II, III and IV,namely, the start, the swing in constant amplitude, the slow movement and the glide. As shown in Fig. 4(a),after reaching the steady state, the velocity in the start stage decreases at first and then gradually increases,the velocity in the stage of the swing in constant amplitude gradually increases, and the rate of increase goes from small to large, and then small, the velocity in the slow stage increases at first and then decreases,the velocity in the glide stage decreases monotonically.
(2) In conjunction with the time history of the acting forceDC in Fig. 4(b), we can analyze the reason why the velocity has a periodic variation. In the start stage,DC gradually changes from drag to thrust, which makescu decrease at first and then increase; in the stage of swinging in constant amplitude,DC is in the constant thrust, and has a peak, thus making the rate of increase ofcu change from small to large, and then small, in the slow stage,CDgradually changes from thrust to drag, so ucincreases at first and then decreases; in the glide stage,CDis in the constant drag, so ucdecreases monotonically. After further study, it is found that bec ause of decreas ing of ucand the n dec reasing of thedrag, CDalsodecreasesintheglidestage,it reduces the rate of decrease of uc.
(3) A comprehensive analysis of the variations of ucand CD, within a burst-and-glide circle shows thatDC changes from the drag to the thrust once during the start stage and changes from the thrust to the drag once during the slow stage. Thuscu takes a minimum and a maximum values during these two stages, respectively. The minimum value is taken after the starting stage and the maximum value is taken before the arrival of the glide stage. It was believed that during the burst phase, the swimmer keeps accelerating[3-4], and the increase and the decrease of the swimming velocity are, respectively, equivalent to the burst and glide phases. But this division is not accurate. Yang et al.[6]and Wu et al.[9]made also similar suggestions, however, they ignored the moment when the minimum velocity appears.
3.2 Transient variation of the flow field
In order to reveal the energy-saving mechanism of the burst-and-glide mode for the thunniform fish, it is necessary to explore the transient variation of the flow field during the fish swimming. From the vorticity distribution generated by the burst-and-glide swimming, we could monitor the transient information of the flow field in the wake region. Figure 5 shows the vorticity contours of the burst-and-glide swimming after reaching the steady state, where Figs. 5(a),5(b) are, respectively, the vorticity contours in the burst-and-glide mode and in the normal self-swimming. Some important characteristics are revealed.
We can see the difference of the kinematics of the burst-and-glide mode and the normal self-swimming: the former includes the four alternate stages of“start-swing in constant amplitude-slow-glide”, while the latter only has the “swing in constant amplitude”stage. The difference of the kinematics directly leads to different vortex structures in the wake. During the start stage and the slow stage of the burst-and-glide swimming, two secondary vortexes are shed off from the left and the right sides of the fish, respectively,which are not fully developed. During the stage of the swing in constant amplitude, a full vortex is shed off in each swinging tail. Figure 5(a) shows the vorticity distribution when =5n , =0.8D . In comparison with the normal self-swimming, in Fig. 5(b), within each cycle, it sheds off alternatively two opposite vortexes, which line up along the vertical direction.
3.3 Effect of swinging tail number on burst-and-glide swimming performance
In this work, we study the mechanism of the burst-and-glide mode for the thunniform fish. Two important parameters, the swinging tail number n and the duty cycle D, are considered, and their effects on the steady swimming velocity are investigated. After reaching the steady state, we can see the effect of n and D on the energetics properties.Finally, from the three-dimensional flow structures,the energy-saving mechanism of the burst-and-glide mode could be revealed physically.
To illustrate the swimming performance, we use the “velocity-power ratio” to see the power variation during the burst-and-glide swimming. According to the velocity-power ratio, i.e.,defined by Schultz[22], the largerv/Pη means less power consumption up to a certain swimming velocity, or less energy loss in swimming some distance. Wu et al.[9]proposed a multi-swinging tail (MT) mode and a half-swinging tail (HT) mode. The kinematics difference of these two modes is that: the former completes a swinging tail action in more than one cycle (i.e.,swinging tail both in the left and right sides), the latter completes the swinging tail action in the left or right half cycle. In the following, we will discuss the effect of the different swinging tail number on the energetics properties.
Figure 6(a) shows the steady swimming velocity U and the thrust coefficientDPC corresponding to the different swinging tail number n when the duty cycle =0.5D . From Fig. 6(a), we know that with the increase of n, U increases, but the rate of increase is small andDPC also increases. This is due to the fact that the thrust effect is mainly related to the burst phase. The distance of several times of the swinging tail means extending the acceleration time. When the duty cycle is given, both the burst phase and the glide phase in generating the continuous swimming become longer, without changing their ratio.

Fig. 6 Relation between energetic parameters and n
Figure 6(b) shows the effect of the swinging tail number on the energetics parameters. It can be observed from Fig. 6(b) that with the increase of n,the power consumptionPLC gradually increases and the rate of increase is small, the efficiency η has a slight increase and the velocity-power ratiov/Pη gradually decreases. Meanwhile, in view of the swimming power and the swimming efficiency, smaller swinging tail number is preferable in reducing the power consumption and increasing the velocity-power ratio. Therefore, in the burst-and-glide mode, we tend to choose a mode with glide and rest once while minimizing the swinging tail number, to save not only the time but also the power. For biological fish, it is a rare case that they choose to swing tail more than twice and then glide. In most cases, they choose swinging tail once or twice, swinging tail once will turn around the fish and swinging tail twice can remain straight.
3.4 Effect of duty cycle on burst-and-glide swimming performance
To further illustrate the effect of the duty cycle on the burst-and-glide swimming performance, Fig.7(a) shows the variations of the steady swimming velocity U and the thrust coefficientDPC agaisnt the duty cycle D. It can be seen from Fig. 7(a) that with D increasing from 0.4 to 0.8, U andDPC are slowly increasing. When =1.0D , it is in the normal self-swimming, and when D increases from 0.8-1.0,U andDPC see certain jumps. The greater the value of D is, the shorter the glide time is when the burst time is given. Figure 7(b) shows the effect of D on the power consumption and the efficiency. From Fig.7(b), we can draw the following conclusions:
(1) With the increase of the duty cycle D, the powerPLC gradually increases, its increase rate is significant and the efficiency η increases slightly.Meanwhile, while D increases from 0.8 to 1.0,PLC and η see certain jumps, and the velocity-power ratiov/Pη gradually decreases. Compared to the normal self-swimming when =1.0D , the smaller the value of D is, the longer the glide time is. And it can consume the least power for obtaining the same steady swimming velocity. Thus the energy can be saved significantly when swimming for the same distance. When D is smaller, the value ofcu obtained decreases a little, but in most of time, it is only needed to keep the swimmer in the straight glide attitude, without doing much work initiatively, so the power consumption is greatly reduced.
(2) Consider the two cases of =0.4D , =0.8D ,as shown in Fig. 7(b) for example, the glide time when =0.4D is much longer than that when D = 0.8, U only decreases by 40%, CPLis reduced by 60%, whilev/Pη increases by 27%. That is to say,for a same swimming distance, the energy consumption of the former is 66.7% of that of the latter, with a longer time to take. During the fish swimming, the glide time can easily be adjusted, which means to adjust the duty cycle. Since the adjustment does not require the consumption of energy, it could be called the passive adjustment.
3.5 Three-dimensional flow structure of burst-andglide swimming
To reveal the energy-saving mechanism of the burst-and-glide swimming, we study the differences and similarities between the burst-and-glide mode and the normal self-swimming in terms of the flow structure and use the q criteria defined[15,23]to extract the vorticity iso-surfaces in two burst-andglide cases and a normal self-swimming case.
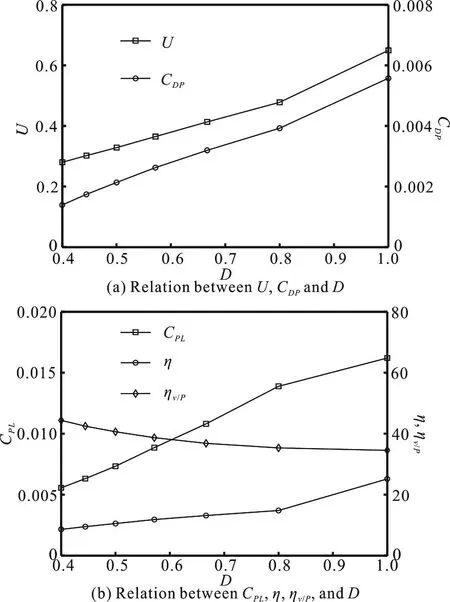
Fig. 7 Relation between energetic parameters and D
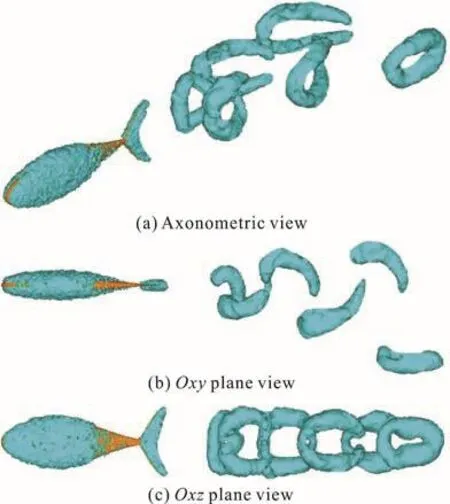
Fig. 8 (Color online) The vorticity iso-surfaces when n = 5 ,D = 0.8
Figure 8 shows three views of the vorticity iso-surface when =5n , =0.8D . From the figure,we can clearly distinguish the wake structures generated in the burst phase and the glide phase. In the burst phase, one sees a series of hairpin-like vortexes,and in the glide phase, one sees no obvious vortex shedding. Therefore, there is an obvious gap between the continuous vortex ring and the body. By careful observation, it can be found that there are not sufficiently developed half vortexes at the beginning and the end of the burst phase, because the two periods of the start mode and the slow mode are contained within the burst-and-glide cycle. In the middle, there are four continuous vortexes resulting from the swinging in the constant amplitude stage.

Fig. 9 (Color online) Comparison of vorticity iso-surfaces
Figure 9 shows the comparison of the vorticity iso-surfaces in two burst-and-glide cases and a normal self-swimming case, which are plotted, respectively,on Oxy plane and Oxz plane. From Fig. 9, we can draw the following conclusions:
(1) It can be found that the wakes are in single row alternating hairpin structures from the comparison of the wakes in these three cases. Both from the two swinging tails in the burst-and-glide swimming and each cycle of the normal self-swimming, two opposite vortexes are shed. And the wake features are consistent with the wake distribution reported by Tytell and Lauder[24]and Neveln et al.[25].
(2) By comparison of the vorticity iso-surfaces when =3n , =0.8D and =5n , =0.8D , it can be found that with different swinging tail number n,the wake structure in the burst-and-glide mode is similar. With the change of n , the difference is that in the burst phase, the number of wake vortex rings in the vortex chain will change. Meanwhile, with the increase of n, the steady swimming velocity gradually increases for a given duty cycle D, and the burst phase and the glide phase are prolonged. Thus,the longitudinal spaces of the burst phase and the glide phase become larger. It should be noted that, when the same n and different D are given, the wake features of the burst phase are the same and only the longitudinal space of the glide phase becomes larger or smaller.
(3) By comparison of the wake features of the burst-and-glide mode and the normal self-swimming mode, the vortex longitudinal length in the wake in the former mode is significantly shorter than that in the latter mode and has more vortexes in the same vertical space. Thus, we have a lower swimming velocity in the former mode. Meanwhile, the wake vorticity strength in the former mode is weaker than that in the latter mode, and correspondingly the energy loss in the wake is less and the power consumption is less too, which is consistent with the above mentioned energetics.
3.6 Comparison of burst-and-glide mode and normal self-swimming
To gain a deeper understanding of the burst-andglide swimming as a kind of energy-saving mode, it is very essential to compare the difference of the energetics between the burst-and-glide mode and the normal self-swimming mode. Table 1 shows the comparison of the energetics for three groups of the burst-and-glide cases and a group of the normal self-swimming case. Both the body and the caudal fin kinematics of these cases are identical. And what is different is that in the normal self-swimming case, we have a continuous swing tail, while in the other three cases of the burst-and-glide swimming we have diffe-rent swinging tail number n and the different duty cycle D. This table reveals several important findings:

Table 1 Energetics comparison between burst-and-glide and normal self-swimming
(1) A comparison of the case 1 and the case 2 shows that with the same n, as D increases, the swimming velocity U, the powerPLC and the efficiency η increase and the glide time and the velocity-power ratiov/Pη decrease. Therefore, it could be deduced that, swimming for the same distance, smaller duty cycle which means longer glide time, can help conserve energy, but the swimming velocity will decrease, so longer time will be taken.
(2) A comparison of the case 2 and the case 3 shows that, with the same D, as n increases, the swimming velocity U, the power coefficientPLC and the efficiency η slightly increase, while the velocity-power ratiov/Pη decreases slightly. Meanwhile, it should be noted that an odd number of swinging tails will make the fish have some degree of turn. The turn is in a maneuvering category, which will not be discussed in this paper.
(3) A comparison of the case 2 and the case 4 shows that with =2n , =0.5D , the burst cyclebT and the glide cyclecT are the same and they are equivalent to the normal swimming cycle T. Therefore, when the fish accelerates for a cycle, it will glide and rest for a cycle and the swimming velocity is about half of that in the normal swimming, while its power consumption is 43.9% of that of the latter, its efficiency is 40.6% of that of the latter and the velocity-power ratio is 1.15 times of that of the latter.Therefore, it can be concluded that swimming for a same distance, in the burst-and-glide mode, more energy can be saved than in the normal self-swimming.
(4) A comprehensive analysis of the above four cases shows that whether in the burst-and-glide mode or in the normal self-swimming depends on a compromise for a high swimming velocity and a low power consumption. Compared with the normal self-swimming, in the burst-and-glide mode, we have a lower swimming velocity and efficiency, as well as a lower power consumption and a larger velocitypower ratio. For swimming a same distance, in the normal swimming, less time will be taken, and in the burst-and-glide mode, longer time will be taken, but with a less power consumption.
4. Conclusions
In the present study, a virtual thunniform swimmer is constructed and employed to elucidate the energy-saving mechanism of the burst-and-glide mode on the basis of the comparison with the normal self-swimming. We systematically study the swimming kinematics and the energetics performance of the burst-and-glide mode for different swinging tail numbers and the duty cycles. As such, we can pose and answer questions that cannot be tackled experimentally due to the difficulties in performing and analyzing the results of the controlled experiments with live fish. The most important findings of our work are as follows:
(1) On one hand, for a given swinging tail number n, as the duty cycle D increases, the swimming velocity U, the power consumptionPLC and the efficiency ηincrease and the glide time and the velocity-power ratiov/Pη decrease. On the other hand,with a fixed duty cycle D, as the swinging tail number n increases, the swimming velocity U, the power consumptionPLC and the efficiency η slightly increase, while the velocity-power ratiov/Pη decreases slightly.
(2) During the burst-and-glide swimming under the self-propulsion, smaller swinging tail number and duty cycle are beneficial in reducing the power consumption and increasing the velocity-power ratio.And thus for obtaining the same steady swimming velocity, the least power is consumed. And to swim for the same distance, significant energy can be saved,however its swimming velocity will decrease, so it will take longer time to cover the distance.
(3) On this basis, the kinematics and the energetics in the burst-and-glide mode are compared with those in the normal self-swimming. These two swimming modes both have advantages and disadvantages. Whether in the burst-and-glide mode or in the normal self-swimming depends on a compromise between the high swimming velocity or the low power consumption. To achieve the same swimming velocity,it is better to be in the normal self-swimming. For swimming the same distance, in the burst-and-glide mode, the power consumption can be significantly reduced. Therefore, a better understanding of the energy-saving mechanism of the burst-and-glide mode can provide a scientific basis for the rational planning of the swimming action for the fishlike robot and for the development of novel and efficient robots.
Acknowledgement
This work was supported by the State Key Laboratory of Robotics and System, Harbin Institute of Technology ( SKLRS-2018-KF-11).
- 水动力学研究与进展 B辑的其它文章
- Call For Papers The 3rd International Symposium of Cavitation and Multiphase Flow
- An integral calculation approach for numerical simulation of cavitating flow around a marine propeller behind the ship hull *
- Numerical study on influence of structural vibration on cavitating flow around axisymmetric slender body *
- An integrated optimization design of a fishing ship hullform at different speeds *
- Critical velocities for local scour around twin piers in tandem *
- Dynamic analysis of wave slamming on plate with elastic support *

