Dynamic analysis of wave slamming on plate with elastic support *

Wei-guang Zuo （左卫广）, Ming Liu （刘明）, Tian-hui Fan （樊天慧）, Jian Chen （陈建）

1. North China University of Water Resources and Electric Power, Zhengzhou 450045, China

2. CCCC First Harbor Engineering Company Ltd. Tianjin 300456, China

3. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510641,China

Abstract: Experiments are conducted to investigate the dynamic response of a plate with elastic support under a regular wave slamming. The statistical analysis results obtained in different model testing cases are presented. The theoretical analysis of the plate vibrations (including the forced and free vibrations) is performed. Four characteristic stages of the plate vibration accelerations between two consecutive wave impacts are identified. The submergence durations of the plate during the wave action and the hydro-elastic effects are discussed. Finally, some useful conclusions are drawn.

Key words: Wave impact, elastic support, vibration acceleration, slamming pressure, hydro-elasticity

Introduction

The wave slamming on offshore structures in the splash zone has been the focus of attention in ocean engineering for the past thirty years. The main studies were centered on the wave impact loads on horizontal structural members. The wave slamming effects on decks of offshore platforms gained little attention.However, the coastwise wharf, the offshore production platform, the marine trestle, etc., are typical offshore and marine open structures above the still water level. The decks of structures are often faced the risk of wave slamming due to the clearance, caused by the defective design of the deck elevation or the structure settlement after a long period operation[1].The enormous impact loads may lead to a global instability or a partial damage of the superstructure in the hostile sea environment.

In view of increasing depletion on the shallow water resources, more and more marine structures,such as the deep-water jacket platform, the tension leg platform (TLP), the semi-submersible platform(SEMI), were built in deeper water[2]. Owing to the shift of marine resources from the shallow water to the deep water, it would inevitably change the integral stiffness of the marine structures from rigid to flexible gradually[3]. In general, the deck clearance might also decrease if higher production volumes were desired in the deep water. This implied a higher risk of wave slamming[4]. Previous studies and engineering applications show that, in the case of inadequate structure clearance, the failure of a concrete or steel structure is not caused directly by strong wave vertical impact loads, but as a result of the accumulation of microcracks, which is due to elastic deformation or vertical vibration of the structure after a long operation[5]. The influence of the structural elastic response on the wave impact pressures will be more and more prominent, which requires investigation.

The research on the wave slamming began in the 1960s. The horizontal members of marine superstructures located in the splash zone were often subject to the wave attack. This could be considered as the water-entry problem of a small-scale horizontal cylinder. The impact force acting on the small-scale horizontal cylinder was expressed in the form of analogous Morrison formula based on the momentum theorem. There were still considerable limitations in the engineering application.

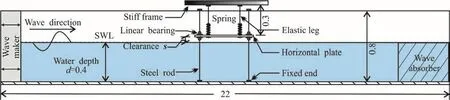
Fig. 1 (Color online) The general layout of experiment (10-2m)

In the case of the wave slamming on the largescale plate in the splash zone, the theoretical and empirical formulas of the wave impact forces based on some assumptions were presented by Baarholm[6].Some different physical model tests were performed to obtain the wave impact force expressions by Zhou et al.[7],respectively. With the development of the computational fluid dynamics (CFD), numerical studies of the wave slamming on a plate were conducted with the numerical models based on the application of the finite element method (FEM), the boundary element method(BEM), the volume of fluid method (VOF), and the smoothed particle hydrodynamics (SPH) method,respectively.

However, as mentioned above, in these studies,the structures were assumed as rigid bodies, ignoring the influence of the structural elastic vibration, the deformation of the structures and the impact pressures.At present, the method of the physical model experiments is commonly adopted for the hydro-elastic slamming problem of a large-scale plate by Tu et al.[8],Shin et al.[9], Ignacio et al.[10]. In the water-entry impact respect, it was presented for the relationships between the elastic response and the natural period of the plate based on the laboratory experimental investigations.Stenius et al.[11]analyzed the deflections and the strains of the marine panel during the water-entry impact. It is shown that the largest hydro-elastic deformation has a time-lag effect, and the most significant hydro-elastic deformation is in places close to the panel support for very flexible structures or sandwich constructions. As to the wave slamming, it was studied for the standing wave slamming on a horizontal plate supported elastically in a flume. It appears that the slamming pressures are strongly depended upon the elasticity of the supports of the plate,thus this problem has to be considered as a problem of hydro-elasticity. The ocean engineering superstructures in the splash zone can be regarded as the rigid body due to the large stiffness. However, the substructures of the support shall be considered as elastic bodies because of the small rigidity. Sulisz and Paprota[12]performed physical model tests to investigate the wave impact on a rigid plate with elastic support. It could be seen that there are four characteristic stages of the structure vibrations between two consecutive wave impacts. Recently, based on the model experiments with elastic support, the dynamic response, the wave slamming pressures, and even the dynamic hydro-elastic effects were analyzed by Liu et al.[13], Song et al.[14].

At present, the wave impact on open structures with elastic support has not been well studied by Yang et al.[15], Chen et al.[16]and Woo et al.[17]. There is no significant progress in this respect due to the lack of the fundamental experiment data for the effects of hydro-elasticity. The focus of this paper is on the slamming pressures due to the elastic support, and the effects of the hydro-elasticity during the wave slamming. The physical model experiments are carried out to investigate the wave impact on the elastically supported superstructure, ignoring the influence of the air cushion. The pressure components and the variation characteristics of the impact pressures during the wave impact underneath the structure models are analyzed.The characteristic stages of the deck vibrations between two consecutive wave slammings are considered. The hydro-elastic effects of the vibration acceleration and the dynamic responses of the plate due to the wave slamming are estimated. Some conclusions based on the experiment results are drawn.

1. Description of experiments

1.1 Experimental setup

The laboratory model experiments are carried out in the oil spilling flume of the State Key Laboratory of Coastal and Offshore Engineering (SLCOE) in Dalian University of Technology (DUT). The wave flume is 22 m long, 0.80 m wide and 0.80 m deep. It is equipped with a DL-3 type irregular wave-maker on the left side, a production of the SLCOE driven by a programmable piston-type system. The wave period made by the wave maker is in a range between 0.5-3.0 s.In the flume is installed an energy-dissipation device on the other side, to absorb the wave energy to reduce or eliminate the influence of the wave reflection. The experimental model of the plate is placed in the middle of the flume as shown in Fig. 1. Detailed sizes of the elastic support in the wave flume are shown in Fig. 2.

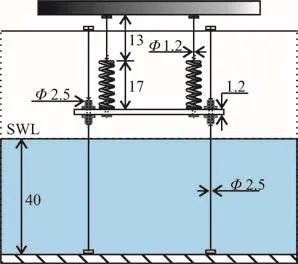
Fig. 2 (Color online) Detailed size of the elastic support and steel pole in the wave flume ((10-2m)

The prototype for an offshore jacket platform is used as the experimental model. The plate is 0.78 m long, 0.78 m wide and 1.20×10-4m thick, and is made of an acrylic glass plate, so that it could be regarded as a homogeneous medium and centrosymmetric rigid body. The mass of the deck is 8.8 kg. The elastic support of the plate is combined by screw steel wires and springs with the total length of 0.30 m. The deck is overhung on the still water level (SWL) by the elastic support and the rigid frame. Three wave gauges are installed in the wave flume to measure the free surface elevations before the deck model, whose positions are denoted by W1, W2 and W3 as schematically shown in Fig. 1.

Fig. 3 (Color online) Arrangement of pressure transducers and accelerometers in the plate model

As mentioned above, a concrete or steel structure failure is mainly due to the accumulation of microcracks formed by the elastic deformation or the vibration of the wave slamming underneath the structure. The motion of the deck in this experiment is restricted in the vertical direction by four combination devices of the smooth steel slider and the linear bearing, which could decrease the damping as much as possible. Consequently, the effect of damping on the free vibration frequencies is very small, practically negligible. The connection positions of the linear bearing (steel pole) and the elastic support (spring) in the deck model, denoted by L1 to L4 and M1 to M4,respectively, are shown in Fig. 3. Eight vertical oscillatory pressure gauges and two vertical piezoelectric accelerometers are installed in the plate to measure the wave slamming pressures and accelerations. The positions of the accelerometers and the pressure transducers, denoted byA1, A2 and P1 to P8,respectively, are shown in Fig. 3.

The wave slamming pressures and accelerations of the plate are measured by using CRIO-9074, a 32-channel synchronous acquisition instrument, developed by the national instruments (NI). The measuring range and the sensitivity of the accelerometers are up to 50 g and 100 mv/g, and the response frequencies of the pressure transducers and the accelerometers are 0.1 MHz and 8 000 Hz, respectively. The sampling interval in the test is 1/1000 s, and the total sampling time is 27 s.

1.2 Free vibrations of deck

The vertical forced vibrations of the plate can be considered as a single degree of freedom (SDOF)system with the deck mass M, the elastic support stiffness K and the damping C, as indicated schematically in Fig. 4.

Fig. 4 (Color online) Vertical forced vibration of a single degree of freedom system

Accordingly, the vibrations of the plate can be described by the following equation, a second order,non-homogeneous, ordinary differential equation(ODE)

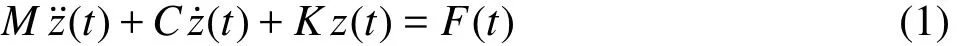
The free vibrations of the plate installed in theempty wave flume are analyzed. The vibrations are started by the initial displacement method and the transient excitation method in the air. For an unforced damping SDOF system, the general equation of motion can be simplified to the following form with the initial conditions

Table 1 Parameters of free vibration of the test models

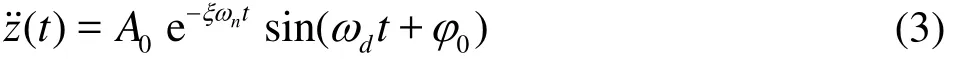
The acceleration corresponding to the vertical vibration mode is obtained from the vertical accelerometers, measured by the gauges A1 and A2 in this test. Since the plate is confined to the vertical movement, the vibration accelerations of the deck contain only the vertical component. The vertical component of the deck acceleration is calculated as the mean value of the accelerations recorded by the gauges A1 and A2. The measured accelerations of the plate and the corresponding amplitudes of Fourier series are indicated in Fig. 5.

The alternate but equivalent solutions of the velocities and the displacements are given by:

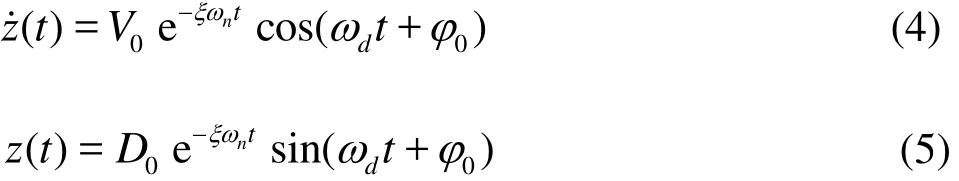
Table 2 Fundamental parameters of wave and model test

Fig. 5 Time series and spectral analysis of incident wave surface

1.3 Test parameters of the model

The incident waves are regular, and the still water depth (d) is maintained at 0.40 m in this experiment. The wave heights ()H are varied from 0.08 m to 0.12 m in an increment of 0.02 m, and the wave periods ()T are chosen as 1.0 s, 1.3 s and 1.6 s.The relative clearance (/ )s H ranges from 0 to 0.4 in an increment of 0.2. The test models include three types with different springs and steel wires. The test cases are determined after a reasonable combination as listed in Table 2. Each case is repeated at least three times to ensure the reliability and the accuracy of the experimental data.

Figure 5 shows the time series and the spectral analysis results of the incident wave surface elevation at the positions of the structure model ( T =1.3s ,H =0.10, 0.12 m). It can be found from the time duration of the wave surface in Fig. 5 that the incident waves display some significant nonlinear characteristics, such as the asymmetry of the wave crest and trough, the higher and steeper wave crest, and the shallower and flatter wave trough. From the amplitude spectrum of the wave surfacein Fig. 5, it is shown that in the incident wave surface series there are at least three main components corresponding to the frequencies =f 0.77 Hz, 1.54 Hz and 2.31 Hz, respectively. The largest amplitude 0.056 m appears at the frequencythen there is the next large amplitude 0.012 m at the double frequencyand the smallest amplitude 0.002 m is near the triple frequency

2. Experimental data analysis

2.1 Wave interaction with deck

The impact pressures caused by the wave slamming are of considerable importance in the design of the coastal structures. The problem of waves interacting with a plate close to the still water level has been studied. The studies show that the vertical slamming pressure on a plate subjected to the intermittent submergence due to the wave impact generally includes components of the slamming pressure, the hydrodynamic pressure, the negative pressure and the zero pressure. These components are illustrated in Fig. 6.However, in view of the various moments of a wave train interacting with the deck, one may study the time duration of the pressures with respect to the free surface ele vation η during a wave period. Fig ure 7 showstheidealizedpressuretimehistoryatthe location of the gauge P1 and the times of occurrence of the four components in terms of the position of the free surface relative to the deck for two types of support, respectively.

It can be seen from Figs. 6, 7 that one first sees a rapid increase and then a sharp decrease of the pressures. This phenomenon corresponds to the instant when a wave surface just contacts the deck underside.The contact causes a sudden transfer of momentum from the wave to the deck, to generate the slamming pressure (SP). One sees a slamming pressure peakat the timelarge in magnitude, short in duration and small in area. This may give rise to the local damage, the fatigue failure and cumulative cracks due to the deck vibrations.

As the wave progresses further, a positive pulsating pressure caused by the deck in contact with the upward water is observed, corresponding to the course when the deck is partially or integrally submerged during the time period when the free surface rises above the upper surface of deck, with some amount of green water on the deck and then a hydrodynamic pressure (HP) on the deck. This pressure is lower in magnitude, longer in duration and larger in area than the slamming one. The pressure grows up firstly then declines to zero with the maximumat the time. The primary cause of the growing tendency is that the deck undergoes an upward pressure,exceeding the weight of the green water on deck. If the upward pressure is equal to the weight of the green water on deck, the peak is reached. However, the declining trend shows the weight is greater than the upward pressure.

Then, one sees a negative oscillating pressure due to the contact of the deck with the downward water, corresponding to the process when the free surface falls from the wave crest and moves forward below the deck. The green water on the deck is reduced, and the negative pressure (NP) is produced.There may be little difference between the hydrodynamic pressure and the negative pressure in magnitude,duration and area. The negative pressure decreases from zero firstly then increases to zero with the minimumat the timeWith the weight of the green water on the deck and a downward pressure,the pressure decreases rapidly and reaches the minimum. As the weight of the green water on the deck reduces, the pressure increases to zero due to the wave recession because the position of P1 is exposed in the air.

Finally, the dynamic pressure in the deck becomes zero (ZP) and the deck vibrates in the air at the instant7( )T of the complete detachment of the wave from the rear edge of the deck.

Fig. 6 (Color online) The duration of wave slamming on plate with rigid and elastic support

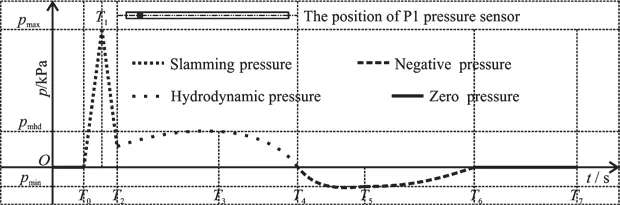
Fig. 7 The idealized time series of wave impact pressures

2.2 Wave slamming pressures

The plate is installed in the wave flume after the measurements of the incident wave profiles. The pressures measured by the transducers fixed at the bottom of the deck provide a physical picture of the impact of the wave with the deck at any time. Figure 8 shows the time series of the pressures on the measuring point P1 for the three test models

Fig. 8 Time series of pressures on the measuring point P1

It can be seen that the slamming pressures grow up with the increase of the stiffness of the supports during the wave impact on the plate with elastic supports. It is designed to be stiff enough for approximating a rigid support for the model of the largest stiffness (TM-03). The slamming pressure peak is about 9.6 kPa. However the peaks of other two models(TM-02 andTM-01) are only 6.4 kPa and 4.6 kPa,respectively.

It is illustrative to see the difference of the wave slamming pressures between the rigid and elastic supports in Fig. 8. The deck with different supports vibrates differently after the impact of the same wave conditions. The deck with an elastic support deviates upward at the instant of the wave slamming. And the smaller the stiffness of the elastic support, the larger the amplitude of the deviation. Consequently, the peak may be reduced and lagged behind the impacting instant of the rigid support. The reduced peak is due to the buffer action of the elastic support against the wave slamming velocity when the maximum occur[18].It can be shown that the importance of the hydroelastic effects for the wave slamming pressures increases with the decrease of the stiffness of the elastic support. However, the amplitude of the deviation of the deck may be very small in the TM-03 due to the fact that the support stiffness is the largest and relatively close to the rigid support in the experiment.For this reason, the occurrence of the peak may be close to the slamming moment1()T and the peak should be greater than those in the other two models.It is interesting to notice that the behavior of the pressure is similar to that on the rigid body in this model[19].

2.3 Wave slamming vibrations

To study the vibrations of the plate owing to the wave impact, the accelerations are measured by the gauges in the deck, for evaluating the interaction characteristics between the wave impact and the deck vibrations at any time. The plate is fixed in the wave flume after the measurements of the incident wave surface. Figures 5, 9 show the time series of the free surface elevations and the vibration accelerations measured by the gauges W2 and A1, A2, respectively.The vertical vibration accelerations of the deck are acquired through taking the average of the values of A1 and A2.

The vertical accelerations of the plate due to the wave slamming experience four characteristic stages as shown in Fig. 9. With the attack of the regular wave crest on the deck undersurface, the vibration is large in magnitude and short in duration, the next is a long duration vibration with the high-frequency component,followed by the vibration of a longer duration and lower frequency, and finally, a free vibration in the air.This corresponds to the described phases of the wave slamming pressures as mentioned above, and described in Ding et al.[20].

Fig. 9 (Color online) Time series of the vibration accelerations between two consecutive wave impacts

The first characteristic stage (S1) is commonly referred to as the wave impact stage. A fast increase,then a decrease of the vibration amplitude is shown in Fig. 9. At the instant of contact between the incident wave crest and the bottom of the plate, a vibration of large magnitude and short duration is caused by the impulsive pressure. The small contact area and the mighty transient impact between the incident wave crest and the elastically supported plate undersurface can generate a vibration of large amplitude and high-frequency. Generally, the large amplitude vibration gives rise the instability or the overthrow failure, even cracks in the concrete in the present engineering. Moreover, the high frequency oscillation brings about more cracks and crack growth and leads to fatigue damages. However, the vibration response will immediately die out due to the effect of the energy loss accompanied by the wave impact breaking.In a word, there are three main features with a great influence on the deck in the first stage, in a small area,with a large amplitude and a duration of millisecond order.

The second characteristic stage (S2) is usually named as the global hydro-elastical stage. The vibration signal attenuation in high-frequency is shown in Fig. 9. The vibration signal does not have a large magnitude and a long duration during the fluid and deck interaction (known as the hydro-elastical effect)at the end of the wave slamming breaking. The signal is extremely complex with many high-frequency components, caused by the positive fluctuating pressure due to the continuous rise of the wave surface and the enlarged contact areas between the fluid and the deck.However, the vibration acceleration is gradually decreased due to the influence of the system damping,the hydro-elasticity and the green water on the deck.The global effect of the waterish deck is evident due to the large magnitude oscillation with a high-frequency component. Moreover, an important physical phenomenon is induced by the effect of the hydroelasticity and the air cushion, as is similar to the so-called the cobblestone oscillation generated by the resonance effect of the air cushion. In addition, the system of the fluid and the deck is in a transitory quasi-static state (a semi-steady state of the dynamic equilibrium) as a result of the hydro-elastical effect after a significant vibration. This is the main reason for the extinction of the high-frequency component.

The third characteristic stage (S3) is generally known as the deck shedding stage. The vibration damping, and first falling and then raising of the frequency are shown in Fig. 9. The consistently small magnitude and the relatively longer duration of the vibration signal can be observed generally. The bottom of the deck is subjected to a negative pressure due to the free surface declining and the shedding the front back from the plate. Due to the fluid damping,the vibration amplitude of the deck decreases. However, at the initial time of the shedding stage, the high-frequency oscillation indicates that the negative pressure breaks the original quasi-static state. And the relatively large amplitude is caused by a very intense interaction owing to the occurrence of the opposite pressure and the jump of the fluid added mass.Moreover, the vibration frequency of the plate in contact with the fluid is incessantly varied due to the variation of the fluid added mass. With the fluid continuous shedding from the deck, the vibration frequency increases due to the diminishing fluid added mass. The elastic support is in a tension condition due to the negative pressure, which can possibly create a longer duration and a delicate balance state.

Fig. 10 The hydro-elasticity duration of wave slamming on plate with elastic support

The fourth characteristic stage (S4) is called the free vibration stage. The unexpected growth and then the continuous damping of the vibration are shown in Fig. 9. The small magnitude and the long duration of the vibration signal can be seen. The deck vibrates in the air as a free rigid body at the end of the water shedding from the plate in this stage. The free vibration dies out gradually due to the system damping. However, the amplitude of the vibration suddenly grows up due to the disappearance of the negative pressure and the decrease of the fluid added mass.

2.4 Hydro-elasticity analysis

The hydro-elasticity (fluid-structure interaction)effects in the slamming problem can be explained by the fact that there is a functional relationship between the slamming pressure acting on the structure and the structural elastic response. In other words, the slamming pressure acts on the structure, and at the same time, the structural elastic response influences the slamming pressure. In many studies of the deck slamming, too much emphasis were put on the slamming pressure peak, without a due attention of the hydroelastic response of the deck. As it is mentioned above,the slamming is localized in time and space with a sudden releases of energy, and the effect of hydroelasticity plays a very important role. So it can be said that the hydro-elasticity should be taken into account if an accurate prediction of the loads is required.

The interaction (partial and integral) time is very important in understanding the slamming processes and the hydro-elasticity effects. In particular, the duration analysis may shed some light into the importance of the dynamic hydro-elastic effects during the wave slamming on the deck. The hydroelasticity (local and global) duration of the slamming is shown in Fig. 9 as the duration of the interaction between the incident wave and the plate. It can be seen that the plate vibrates dramatically and the duration is different due to varied stiffness after contact with the fluid. So the duration of the interaction (S1, S2 and S3) between the fluid and the plat is usually used as a variable parameter to measure the hydro-elasticity effect. In order to understand the importance of the hydro-elasticity, the non-dimensional interaction durationis considered as a function of the ratiobetween the period of natural vibration of the dry deck and the incident wave period as shown in Fig. 10.

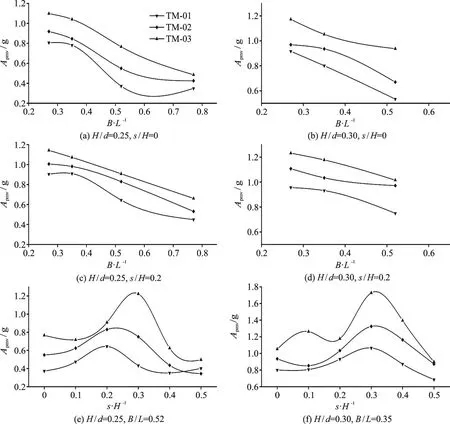
Fig. 11 The relationship between positive maximum acceleration and relative plate length and clearance

It is worth noting that the hydro-elasticity duration is significantly reduced during the wave slamming in Fig. 10. The remarkable reduction tendency caused by the increasing ratio indicates that the elastic support stiffness of the plate influences the hydro-elasticity duration. It should be noticed that the greater the support stiffness, the less the hydroelasticity duration, the larger the vibration acceleration,as shown in Fig. 9. However, when the ratio becomes greater than 1.3, the reduction trend is not particularly evident, which may indicate that the effect of the hydro-elasticity does not play a significant role here.

Figure 10 shows that the hydro-elasticity duration increases as the relative clearance (/ )s H of the plate gradually decreases. As the relative clearance increases, the green water on the deck falls off and the interaction area reduces during the wave slamming.This may be due to the fact that the smaller the value of /s H, the more important is the effect of the hydro-elasticity. It is also important to mention that the hydro-elasticity duration increases with the decrease of the relative deck length (/)B L. The smaller the relative deck length, the more the green water and the larger the interaction area, which also influences the duration during the wave slamming.

2.5 Dynamic analysis of deck

More light can be shed to the physics of the wave impact on the plate by the analysis of experimental data. The important problem in the impact is the structural response in terms of the deck vibration, as a function of different parameters that influence the slamming interaction. In view of the above experimental parameters, the deck vibration may be expressed in the form

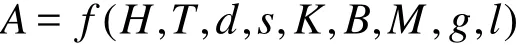
However, in engineering applications, the maximum acceleration is of particular interest and its dimensionless form can be expressed as

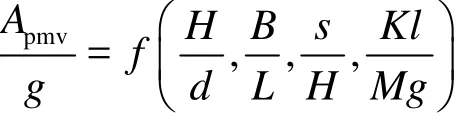
The performed analysis combined with the experimental observations indicates that there may be a close relationship between the vibration accelerations and the elastic support stiffness of the plate during the wave slamming. Figure 11 shows that the acceleration increases with the increase of the stiffness,this tendency corresponds to the variation of the wave slamming pressure as shown in Fig. 8. It should be noticed that the vibration acceleration reduces as a function of the relative deck length, but the acceleration increases gradually due to the increase of the elative wave height during the wave slamming.

It is also found that the vibration acceleration increases firstly, and then decreases with the growth of the relative clearance. This phenomenon can be explained by the fact that the smaller the relative clearance, the more important is the effect of the air cushion, and the smaller the acceleration. However,the larger the relative clearance, the more the skipped air and the smaller the slamming velocity, the smaller the acceleration. The maximum acceleration often appears when the relative clearance is in the range between 0.2 and 0.3 due to the larger slamming velocity and the less important effect of the air cushion. The variations of the vibration acceleration are similar to the slamming pressures of the wave action on a rigid structure. A comprehensive study can be found in Ref. [19].

3. Conclusions

In this paper, the laboratory model experiments are carried out to study the dynamic response of the elastically supported plate due to the wave slamming.Experimental data are analyzed with emphasis on the wave-induced vibrations. Some conclusions could be drawn as follows:

(1) Four characteristic stages between two consecutive wave impacts can be identified. Those are the wave impact stage, the wave-deck interaction stage, the deck-shedding stage and the free vibration stage, respectively. The first stage duration is different due to the elastic support stiffness. With the decrease of the support stiffness, the occurrence time of the peak slamming pressure slightly lags behind the moment of the wave contact with the deck.

(2) The variation of the submergence (partial and integral) duration during the wave slamming against the elastic support stiffness is found. The smaller the elastic support stiffness is, the longer the submergence duration and the larger the peak slamming pressure.

(3) A close relationship between the movement and the elastic support stiffness of the plate during the wave slamming is revealed. This may be the reason why the submergence duration increases with the decrease of the support stiffness. The smaller the value of the relative clearance (/ )s H is, the more important the effect of the hydro-elasticity is. The smaller the relative deck length is, the more the green water and the larger the interaction areas are.

(4) The vibration acceleration increases firstly,then decreases with the growth of the relative clearance. The maximum acceleration often appears when the relative clearance is in the range between 0.2 and 0.3 due to the large slamming velocity and the neglect of the effect of the air cushion.

Acknowledgements

This work was supported by the China Postdoctoral Science Foundation (Grant No. 2017M612669),the Fundamental Research Funds for the Central Universities (Grant No. 2017BQ089), the Key Scientific Research Projects in Henan Province (Grant No. 18B570005) and the Open Research Foundation of Key Laboratory of the Pearl River Estuarine Dynamics and Associated Process Regulation,Ministry of Water Resources (Grant No. [2017]KJ01),Collaborative Innovation Center of Water Resources Efficient Utilization and Protection Engineering in Henan Province, Henan Key Laboratory of Water Environment Simulation and Treatment, Henan Provincial Hydraulic Structures Safety Engineering Research Center.