Improving robustness of complex networks by a new capacity allocation strategy
Jun Liu(刘军)
Department of Information Science and Technology,Tianjin University of Finance and Economics,Tianjin 300222,China
Keywords: capacity,cascading failure,complex network,robustness
1. Introduction
In the past few years,complex network theory has developed rapidly and has been used to study robustness of infrastructure network against cascading failures,such as transportation networks,[1,2]logistics network,supply chain networks,[3]and power grids.[4,5]Cascading failure can make great damage to infrastructure networks,which can be described as follows. If there are some nodes fail, it can cause the redistribution of loads, which may make the loads of some nodes exceed their capacities, so the failures scale will be continuously expanded,eventually,resulting in collapse of the entire network. Cascading failure is fatal to the functioning of infrastructure networks. These infrastructure networks are important for us,once they are destroyed,it will seriously affect people’s production and life and cause great property losses.In June 2019,Argentina and Uruguay suffered massive power outages across the country.The blackout also affected cities in Paraguay,southern Brazil,and parts of Chile. What is worse,the power outages have led to water and gas shortages in five South American countries, as well as the closure of subway,bus and intercity railway, which have severely affected residents’ lives. So cascading failures[6–9]and robustness[10,11]of infrastructure networks are paid more attention by scholars because of their great importance. Chen et al.[12]researched controllable robustness on networks with considering the external or internal failure.Jing et al.[13]constructed a cascading failure model by considering time delay in failure propagation process and considered the effect of the node recovery probability on cascading failures.
As we all know, there exists load on nodes in infrastructure networks.[14]So the failure of nodes can cause the redistribution of the load. And it will make the load of some nodes exceed their capacities,which can lead to further overload failures and ultimately spread over the entire network. In order to improve the robustness of complex networks against cascading failure, scholars have researched from different perspectives,such as the initial load of node, the capacity allocation strategy, and load redistribution strategy.[15–18]. Motter et al.[15]proposed a classical ML load model,which consider that network information was exchanged along the shortest path between nodes, so they defined the betweenness of a node as its initial load. At the same time, they assume that the capacity of a node is proportional to its initial load due to the cost limit,this capacity allocation strategy is adopted in many researches.[18–21]The ML model requires each node to master the whole information of the network. So,it is appropriate for small networks. In fact the global information is hard to obtain,especially for large scale networks.And in the actual network system the load may not be transmitted along the shortest path,such as public transport network. Wang et al.[22]defined the initial load of node as the product of the degree of node and the sum of the degree of its neighbors,which is in positive correlation with betweenness centrality.[23]Considering both local and global information,Liu et al.[24]defined the load of a node by combining the node degree with the betweenness. We all know that cascading failures do not occur as long as the capacity of the node is large enough.However,capacity is costly,the capacity of a node cannot be infinite. So it is very meaningful to study the capacity allocation strategy under limited resources, which has great effect on the network robustness.However,there is not much literature on the dynamical capacity allocation procession to resist the cascading failure. Wang et al.[25]proposed an improved capacity model based on ML model, and defined the cost to protect vertices. According to the definition of cost,their model has always a lower value of the cost than ML model. However, in this model, there will be no fault-tolerant capacity for some nodes if β /=0, which is unreasonable. Because the load on a node usually fluctuates in real network, and the network will not work properly due to the presence of these nodes without fault-tolerant capacity. Li et al.[26]also proposed an improved capacity model based on ML model. Different from ML model, the faulttolerant capacity and topological structure are interrelated in their model,which can achieve better network robustness. But the model considered that network information was exchanged along the shortest paths between nodes. In fact, the loads in some real networks are not always exchanged along the shortest paths.[17]To solve this problem,Wang et al.[17]proposed a load redistribution strategy based on local information. Since then,more and more scholars[20,21,27]began to study the load redistribution strategy based on local information or to use the load local redistribution strategy to study the cascading failure. And most of them considered that the capacity of the node is proportionate to its initial load which was proposed in ML model.
Based on the above analyses, we put forward a new capacity allocation strategy based on the community structure,meanwhile we use the load local redistribution strategy to research the robustness of complex networks. And in order to demonstrate the effectiveness of the new strategy, a comparison was made with the capacity allocation strategy of ML model.
2. Capacity allocation strategy and cascading failure model
Cascading failures of the network can be described as follows, each node has an initial load L(0) and load capability C, under normal circumstances, L(t)<C, the network is in the steady state. After the node is removed (attacked or mechanical failure),the load on the failed node is redistributed to its neighbors. If the capacity of the neighbor is not enough to handle the extra loads,the neighbor would collapse,which can lead to load-redistribution and further overload failures and finally result in the collapse of the entire network. Assume that the potential cascading failure is caused by the removal of one single node, then we pay attention to the following dynamic process of the network. Cascading failure model used in this paper is briefly described as follows.
2.1. Definition of initial load
The initial load of node j is set as

where Lj(0) is the initial load of node j, kjand Γjare the degree of node j and the set of neighbors of node j, respectively. θ is a tunable parameter and governs the strength of the node load. The definition of initial load is reasonable because the product of the degree of node and the sum of the degree of its neighbors is in positive correlation with betweenness centrality.[28,29]
2.2. Capacity allocation strategy
In the existing model, one model should be paid special attention: the capacity allocation strategy in Motter–Lai(ML)model,[15]which is widely used to study cascading failures in complex networks. The ML model assumes the capacity of node j is proportional to its initial load as

where β (≥0)is a tolerance parameter representing the extra capacity.
In this paper, we put forward a new capacity allocation strategy against cascading failures,as folows:

In the new capacity allocation strategy model proposed in this paper,the cost is
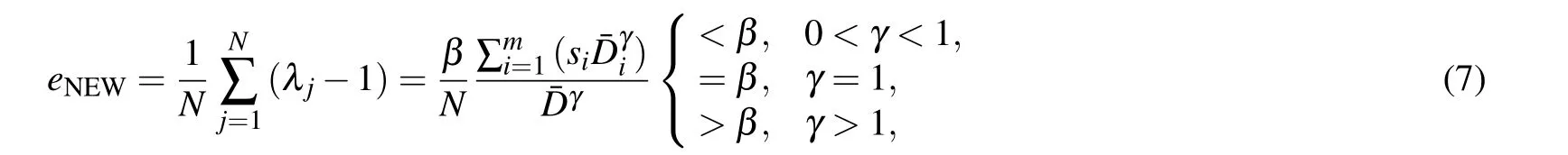
where siis the number of nodes in community i.
Different from ML model,the fault-tolerant capacity and community structure are interrelated in the current model,and the intensity of correlation is controlled by γ.Considering that each component of the network may have different fault tolerance capabilities,this work proposes a more general allocation strategy to allocate additional capacity.
2.3. Load-redistribution strategy
Considering the time-varying load and the time-varying residual capacity, we adopted the method in Ref.[31], which can be defined as
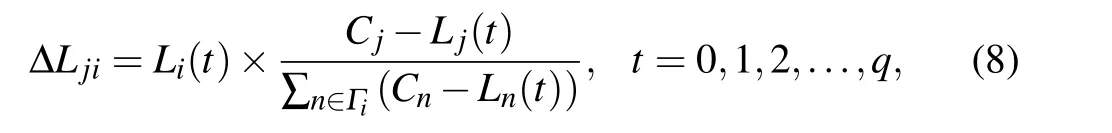
where ΔLjiis the extra load that node j should obtain from the failure node i,Cjis the capacity of node j,Lj(t)is the load of node j at the time step t,q is the number of time steps before the cascading process stops. j is the nearest neighbor of node i,Γiis the set of the nearest neighbors of node i.
So at the time step t+1,if Lj(t)≤Cj,the load of node j is
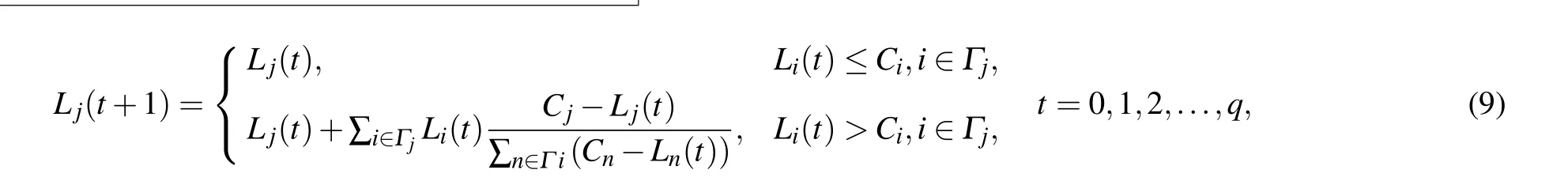
where Γiis the set of the nearest neighbors of node j.
3. Simulation and analysis
According to Ref. [31], Piis used to evaluate the size of the cascade due to the removal of node i

where Fiis the number of failure nodes caused by the removal of node i. N is the total number of nodes in the complex network.
The average size of the cascade due to the removal of one node can be described as

In this paper, we focus on cascading failure triggered by the removal of a single node. And to measure the overall level of the network robustness against cascading failures due to the removal of a single node,we randomly remove only one node(such as node i)each time,and calculate the proportion of failure nodes(Pi)induced by removing node i.Remove a different node each time until all nodes have been removed once. Then the average proportion of failure nodes P is calculated according to Eq.(11)to evaluate the overall level of the network robustness against cascading failures. Each result is the average value of more than 20 realizations for the same topology.
Two artificial network models are tested, i.e., Erd¨os–R´enyi model and the Barabasi–Albert (BA) model.[32]The two typical complex networks used in this paper are all generated by Pajek with network size N=1000 and average degree〈k〉=8. Furthermore,US power grid network as real complex network is considered. US power grid network is the highvoltage power grid in the Western States of the United States of America. There are 4941 nodes and 6594 edges in the power grid of the western United States. The nodes are transformers, substations, and generators, and the ties are high-voltage transmission lines.
Many literatures assume that node load is constant when studying network robustness,but in fact,node load is variable.Hence, in order to verify the effectiveness of our method, we conduct experiments from two aspects,i.e.,the load in the network is constant during normal operation and the load in the network is time-varying during normal operation.
The time-varying load Li(0)of node i can be defined as
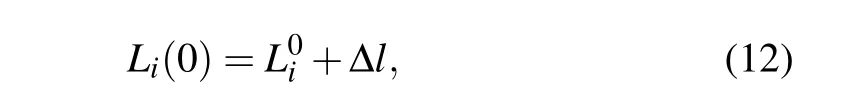
where Δl is the disturbance variable,it can be defined according to the variation trend of the load. Here,in order to explore the effectiveness of the model for simplicity,Δl=βL0iεi,εiis a random number between-1 and 1.
First of all,we compare and analyze the new strategy and ML method based on two typical networks.
Figure 1 shows the experimental results in BA network.From Fig.1 one can see that the new strategy(as shown in the line) can effectively reduce the scale of cascade failure compared with ML model(as shown in the dotted line)in BA network regardless of whether the load is variable or fixed. And with other parameters unchanged, the cascading failure scale decreases as the value of γ increases. γ is an adjustable parameter in Eq.(3),the smaller the value of γ is,the more homogeneous the capacity of node is. With the increase of γ,capacity resources tend to be allocated to communities with high average node degree. The experimental results indicate that allocating more capacity resources to the community with high average node degree is beneficial to reduce the scale of cascading failure. In Fig. 1, with the increase of β, the scale of cascading failure decreases,and one can see that cascading failures can be avoided if the capacity is large enough,which is consistent with the actual situation. Meanwhile,we can find that the scale of cascading failure decreases with the increase of θ for the same β, γ, which means that the more heterogeneous the initial load of the network nodes is, the stronger the overall destruction resistance of the network will be. But this kind of network can be vulnerability to deliberate attack with the increase of θ (shown in Fig. 7). Furthermore, comparing Figs.1(a),1(c),and 1(e)with Figs.1(b),1(d),and 1(f),we can find that the scale of cascading failure under constant load condition is lower than that under time-varying load condition, which indicates that BA network is more vulnerable under time-varying load condition.

Fig.1. The average proportion of failure nodes P as a function of β and γ based on ML model and new strategy in BA networks for different θ. (a)Constant load, θ =0.4; (b) time-varying load, θ =0.4; (c) constant load, θ =1; (d) time-varying load, θ =1; (e) constant load, θ =1.6; (f) timevarying load,θ =1.6. The dotted curves reflect the relationship between P and β for different θ and γ based on ML model. The solid curves present the relationship between P and β for different θ and γ based on new strategy.

Fig.2. The average proportion of failure nodes P as a function of β and γ based on ML model and new strategy in ER networks for different θ.(a)Constant load,θ =0.4;(b)time-varying load,θ =0.4;(c)constant load,θ =1;(d)time-varying load,θ =1;(e)constant load,θ =1.6;(f)time-varying load,θ =1.6. The dotted curves reflect the relationship between P and β for different θ and γ based on ML model. The solid curves present the relationship between P and β for different θ and γ based on new strategy.
Figure 2 shows the experimental results in ER network.As can be seen from the experimental results,compared with the capacity allocation strategy proposed in ML model, the new strategy also can reduce the scale of cascading failure most of the time even though it is not obvious. For the random network,the average degree of each community does not differ much,so the effect of the new strategy is not obvious.In Fig.2,P is decreasing with the increase of β for the same θ,γ,which is consistent with the basic theory that there will be no cascading failures as long as the network has sufficient capacity. And focus on the effect of θ on the robustness of complex network,one can see that in ER network P is decreasing with the increase of θ. But the effect is not obvious in ER network compared with that in BA network. Moreover, considering the comparative analysis under constant node load and timevarying load, almost all the results (Figs. 1 and 2) show that the network is more vulnerable under time-varying load condition. Although the load redistribution strategy adopted in this paper has considered the time-varying characteristics of the load, the random variation of the load makes the distribution of the residual capacity in the network uncontrollable.For example,large load nodes may have little surplus capacity while low load nodes have relatively high surplus capacity. So capacity cannot be fully utilized due to the unreasonable distribution of residual capacity, which increases the network’s vulnerability.
In order to show the effect of the new strategy more intuitively,we introduce indicator w,as

where PMLis the average size of the cascade under the ML model, PNewis the average size of the cascade under the new capacity allocation strategy.
Considering that the overall destruction resistance of the network is stronger with θ =1.6,we analyze the effects of β and γ on w with θ =1.6 in two typical networks.
From Fig. 3 one can see that the new strategy improved the robustness of BA network compared with the strategy of ML model,and the robustness of BA network is gradually enhanced with the increase of γ regardless of whether the load is variable or fixed. The performance of the BA network against cascading failures has been improved by nearly 90%when β =0.13 and γ =1.9 (as shown in Fig. 3(a)). Meanwhile, we find that wincreases as βincreases, but wpresents a downward trend when β >1.3, which indicates that there is a β =βmaxthat maximizes w for each γ. A similar conclusion can be drawn on random networks,which can be seen in Fig. 4. However, the performance of the ER network against cascading failures has been improved by nearly 10%based on the new strategy,which is much less than that in BA network.
Although the cost for the two methods (i.e., ML model and the new strategy)can be calculated by Eq.(5),cost cannot be used to judge the merits of the two methods.And the impact of capacity cost on network destructiveness is more suitable as an evaluation index. So we introduce contribution rate of unit capacity to network robustness Q,which is defined as

The larger Q is,the higher the capacity utilization is.

Fig.3. Indicator w as a function of β and γ for fixed θ =1.6 in BA network,with N=1000 and〈k〉=8. (a)Constant load and(b)time-varying load.

Fig.4. Indicator w as a function of β and γ for fixed θ =1.6 in ER network,with N=1000 and〈k〉=8. (a)Constant load and(b)time-varying load.
From the results shown in Fig.5,one can see that Q goes up and then goes down with the increase of β in BA network.In other words,there is a β =βmaxthat maximizes Q for each θ. It indicates that it is not economical to increase the cost of capacity when β >βmax. Meanwhile, the scale of cascading failure has been reduced to a very low level when β =βmax,which can be seen in Fig. 1. So β ≤βmaxis a more reasonable range of β in the actual networks. Compared with ML model, our method can achieve a higher Q for the sameβ,when β ≤βmax. It indicates that the new strategy is more efficient in using network capacity. Figure 6 shows the experimental results in ER network.As shown in Fig.6,at the beginning Q increases with the increase of β,but once β reaches a certain value,Q stops growing as β goes up.Meanwhile,compared with ML model, the new strategy can achieve a higher Q for the same β in ER network even though it is not obvious.Comparing Fig.5 with Fig.6, one can see that the new strategy is more advantageous in the rational utilization of network capacity in BA scale-free network.

Fig.5. Q as a function of βand γ for different θ under different strategies in BA networks: (a)constant load,θ =0.4;(b)time-varying load,θ =0.4;(c)constant load,θ =1; (d)time-varying load,θ =1; (e)constant load,θ =1.6; (f)time-varying load,θ =1.6. The dotted curves are the results of ML model. The solid curves are the results of the new strategy.
Although typical model networks are useful in understanding how real networks behave, they cannot catch many of the structural properties of the real systems. Therefore,we consider a real complex network,i.e.,US power grid network.Here we mainly study its robustness against deliberate attacks.So we selected the top 10 highest degree nodes in US power grid network. And each time only one of the ten nodes is removed, then the size of the cascade Pidue to the removal of the node is calculated. The average size of the cascade due to the removal of one node can be described as

where Γ represents the set of the top 10 highest degree nodes.
As you can see from Fig. 7, our new strategy still performs well against deliberate attacks on real network,whether the load is fixed or time-varying. When parameter θ is small,cascading failure scale is more sensitive to the change of β. it can be seen in Fig.7(a),When β increases from 0.09 to 0.21,P10can decrease from 1 to 0. However,with the increase of θ,the effect of the increase of β on improving the robustness of the network against deliberate attacks becomes less obvious.It indicates that the increase of θ can reduce the robustness of the network against deliberate attacks if the capacity cost is fixed.Moreover,the increase of γ can improve the robustness of the network against deliberate attacks when other parameters are fixed.

Fig.6. Q as a function of β and γ for different θ under different strategies in ER networks: (a)constant load,θ =0.4;(b)time-varying load,θ =0.4;(c)constant load,θ =1; (d)time-varying load,θ =1; (e)constant load,θ =1.6; (f)time-varying load,θ =1.6. The dotted curves are the results of ML model. The solid curves are the results of the new strategy.

Fig.7. P10 as a function of β and γ for different θ under different strategies in US power grid networks. (a)Constant load,θ =0.4;(b)time-varying load,θ =0.4;(c)constant load,θ =1;(d)time-varying load,θ =1;(e)constant load,θ =1.6;(f)time-varying load,θ =1.6. The dotted curves are the results of ML model. The solid curves are the results of the new strategy.
Furthermore,we research the contribution rate of unit capacity to network robustness Q in US power grid network.From the experimental results, we can see that our new strategy has a higher capacity utilization. And from Fig.8,one can see that Q is decreasing with the increase of θ. It is reasonable because the heterogeneity of the network becomes more obvious with the increase of θ. And heterogeneous networks are vulnerable to deliberate attacks by high degree nodes. So the contribution rate of unit capacity decreases as θ increases.When θ is small, the value of Q increases rapidly with the increase of β,which indicates that the network with homogeneous load distribution can effectively improve its robustness against deliberate attacks by increasing capacity cost. When θ is big, the value of Q grows slowly with the increase of β,which indicates that network with heterogeneous load distribution cannot resist the deliberate attack on generous nodes simply by increasing capacity cost.
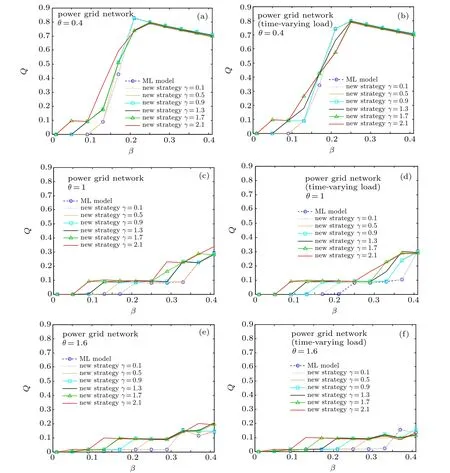
Fig.8. Q as a function of βand γ for different θ under different strategies in power grid networks: (a)Constant load,θ =0.4; (b)time-varying load,θ =0.4; (c)constant load, θ =1; (d)time-varying load, θ =1; (e)constant load, θ =1.6; (f)time-varying load, θ =1.6. The dotted curves are the results of ML model. The solid curves are the results of the new strategy.
4. Conclusions
The cascading failure is a crucial process in many real systems,which can cause significant damage to network functions. Limited network capacity is a necessary condition for cascading failures, but the capacity of real system cannot be infinite. Changing the topology of the network can effectively improve the robustness of the network, but the topology of many existing network systems is not easy to change. So it is very important to allocate the limited network capacity reasonably without changing the network topology.
In this paper, we developed a new strategy to allocate the limited capacity for suppressing cascade failure. Through comparison experiments,one can see that the new strategy can effectively reduce the scale of cascading failure. And it works better in scale-free networks than in random networks. Furthermore,we find that capacity efficiency is not monotonically increasing as the cost of capacity increases,that is to say,there is a cost threshold βmax. It is not economical to improve network robustness by increasing capacity costs when the cost is higher than βmax. And the capacity utilization of the new strategy is higher than that of ML model when the cost is lower than βmax. Meanwhile,the increase of γ can improve capacity utilization when β ≤βmax. Furthermore, it is found that cascading failures are more likely to occur when the network load is time-varying through comparative analysis.
- Chinese Physics B的其它文章
- Numerical simulation on ionic wind in circular channels*
- Interaction properties of solitons for a couple of nonlinear evolution equations
- Enhancement of multiatom non-classical correlations and quantum state transfer in atom–cavity–fiber system*
- Protein–protein docking with interface residue restraints*
- Effect of interaction between loop bases and ions on stability of G-quadruplex DNA*
- Retrieval of multiple scattering contrast from x-ray analyzer-based imaging*

