四象限工况单双泵控差动缸控制性与效率对比
张树忠 PIEOLA 黄豪杰
(1.福建工程学院机械与汽车工程学院, 福州 350108; 2.福建省机床行业技术创新公共服务平台, 福州 350108;3.阿尔托大学机械工程系, 埃斯波 14400; 4.数字福建工业制造物联网实验室, 福州 350108)
0 引言
电液控制系统有阀控系统和泵控系统两大类。能源短缺和环境污染问题的日趋严重,使能量利用率较低的电液控制系统成为节能减排研究的热点。阀控系统管路损失大、系统效率低,大量的重力势能和制动能转为热能,造成系统发热;与阀控系统相比,泵控系统取消了流量控制阀,消除了节流损失,大大提高了系统效率。
泵控缸系统包括泵控对称缸和泵控非对称缸(差动缸)。泵控对称缸技术起步相对较早[1],并已在飞机控制等系统中得到了广泛应用[2]。而泵控差动缸由于液压缸两侧的有效工作面积不一致导致流量不平衡,许多学者和研究机构对此开展了相关研究[3]。如采用双电动机双定量泵或多泵[4-7]、单电动机驱动单定量泵或变量泵加补偿回路[8-12]、单电动机驱动专用非对称泵[3,13-16]来实现差动缸的流量平衡。
其中,单电动机驱动单定量泵或变量泵控差动缸系统的动力元件相对较少、结构相对简单,但需要较大流量的补偿回路,且在速度方向不变、负载方向改变时,易出现大幅度的速度和压力波动。为提高该系统平稳性,需要采用复杂控制策略来抑制速度波动[17-18]。为此,本文提出一种单电动机驱动双定量泵控差动缸的系统方案及控制方法,建立变转速单泵和双泵控差动缸系统模型,开展双泵控缸试验,通过仿真分析对比两种系统性能。
1 系统结构和四象限工况运行原理
1.1 变转速单泵控差动缸系统
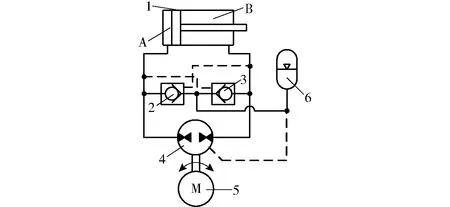
图1 变转速单泵控差动缸系统原理图Fig.1 Schematic of single pump controlled differential cylinder with variable speed1.差动液压缸 2、3.液控单向阀 4.双向定量泵/马达 5.伺服电动机/发电机 6.液压蓄能器
变转速单泵控差动系统主要包括差动液压缸、一对为低压侧补油或排油的液控单向阀、双向定量泵/马达、用于代替低压油箱的液压蓄能器以及伺服电动机/发电机,如图1所示。
根据液压系统对外做功或者进行能量回收可将该系统的4种工况分为以下两类:对外做功——外力F方向与活塞杆速度v的方向相反,见图2中的Ⅱ和Ⅳ象限。此时,进油腔为高压腔,泵/马达工作在泵工况,电动机/发电机则为电动机工况。能量回收——外力F与活塞杆速度v的方向相同,见图2中的Ⅰ和Ⅲ象限。此时,回油腔为高压腔,泵/马达工作在马达工况,电动机/发电机则为发电机工况。
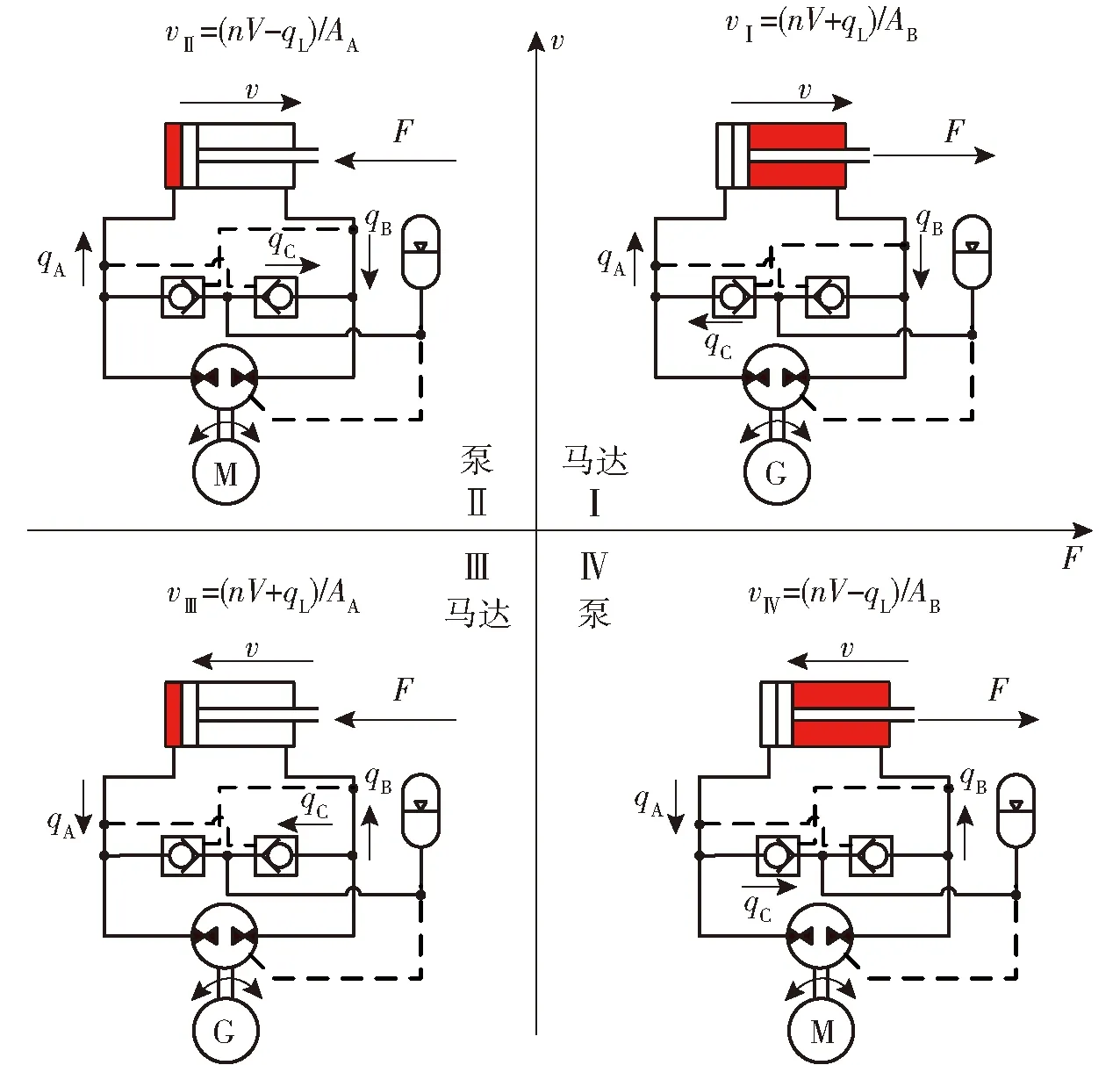
图2 变转速单泵控差动缸四象限工况图Fig.2 Four-quadrant operating principle diagram of single pump controlled differential cylinder with variable speed
假设泵/马达在泵工况和马达工况下的泄漏相同,忽略液压缸的泄漏,对四象限工况运行原理进行分析。
(1)Ⅰ象限中,泵/马达工作在马达工况,高压腔即控制腔为小腔B;则液压缸速度vⅠ与转速n的关系为
vⅠ=(nV+qL)/AB
(1)
式中AB——小腔B工作面积,m2
V——泵/马达额定排量,m3/r
qL——泵/马达泄漏流量,m3/s
(2)Ⅱ象限中,泵/马达工作在泵工况,控制腔为大腔A,则液压缸速度vⅡ与转速n的关系为
vⅡ=(nV-qL)/AA
(2)
式中AA——液压缸大腔A工作面积,m2
(3)Ⅲ象限中,泵/马达工作在马达工况,控制腔为大腔A,则液压缸速度vⅢ与转速n的关系为
vⅢ=(nV+qL)/AA
(3)
(4)Ⅳ象限中,泵/马达工作在泵工况,控制腔为小腔B,则液压缸速度vⅣ与转速n的关系为
vⅣ=(nV-qL)/AB
(4)
液压缸活塞杆伸出过程(Ⅰ和Ⅱ象限)或缩回过程(Ⅲ和Ⅳ象限)中 ,若负载方向发生改变,使控制腔发生交换,将导致活塞杆速度的剧烈波动;假设泵/马达转速n不变且总泄漏系数均为KL,则速度比α为
(5)
假设泵/马达的总泄漏系数KL为4%~9%,AB/AA=0.64(差动缸杆径为30 mm,缸径为50 mm),则速度波动率(1-α)为12.8%~30.8%。随着泄漏流量和面积比的增加,其速度波动愈剧烈。
1.2 变转速双泵控差动缸系统
为了克服在液压缸伸出或缩回时,因负载方向改变引起的速度大幅度波动而影响系统平稳性和精确性,提出一种变转速双泵控差动缸的系统方案,见图3。该系统包括差动液压缸、一对用于防止气蚀的单向阀、代替油箱的低压液压蓄能器、一对排量比与液压缸面积比基本一致的定量泵/马达以及伺服电动机/发电机。
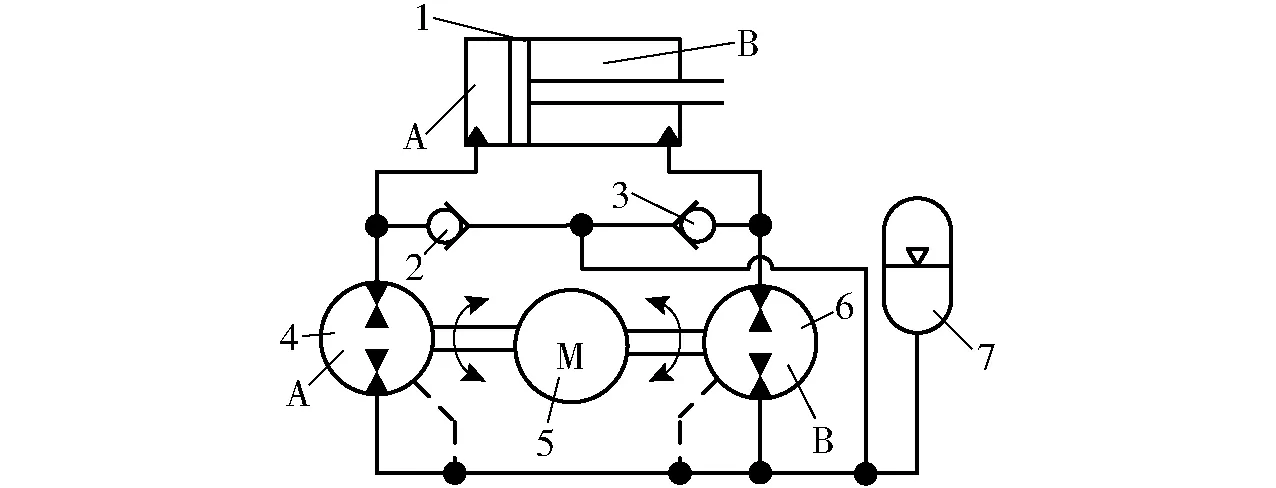
图3 变转速双泵控差动缸系统原理图Fig.3 Schematic of double pump controlled differential cylinder with variable speed1.差动液压缸 2、3.单向阀 4、6.定量泵/马达 5.伺服电动机/发电机 7.液压蓄能器
同样根据施加在液压缸活塞杆上的外力F和运行速度v,将其分为如图4所示的4种工况。在能量回收工况中,Ⅰ象限的泵/马达B和Ⅲ象限的泵/马达A处于马达工况;在对外做功工况中,Ⅱ象限的泵/马达A和Ⅳ象限的泵/马达B处于泵工况。
在活塞伸出或缩回过程中,假设泵/马达的转速n不变且泄漏流量qL的系数均为KL, 由于外力方向改变,导致工况在第Ⅰ和Ⅱ象限之间或第Ⅲ和Ⅳ象限之间相互切换时,其速度比分别为
(6)
(7)
式中VA、VB——泵/马达A、B额定排量,m3/r
Rideal——系统中液压缸小腔面积AB与大腔面积AA之比
Rreal——泵/马达B和A的排量比

图4 变转速双泵控差动缸四象限工况图Fig.4 Four-quadrant operating principle diagram of double pump controlled differential cylinder with variable speed
在速度方向不变,负载方向改变,泄漏系数KL为4%~9%时,速度波动率为8.3%~19.8%。因此,此系统宜选择容积效率较高的定量泵。
为减小或者避免因负载方向改变而导致速度大幅度波动,选型中应使Rideal与Rreal相等或者基本相等。但实际中由于泵/马达排量比Rreal受限于厂家生产的泵/马达的规格型号,难免导致有一定的选型偏差。此时,排量不足的一侧回油过慢引起压力逐渐升高,导致系统效率在一定程度上降低[19]。选型偏差为
(8)
系统中,为了避免油液压缩或者膨胀、液压缸和泵/马达的泄漏以及选型偏差而引起气蚀,增加了一对单向阀来实现低压侧的补油。
综上所述,可知变转速双泵控差动系统较单泵控差动缸系统具有更好的速度控制特性。
2 系统建模
为了模拟液压系统的四象限工况,以1 t微型液压挖掘机工作装置中的斗杆液压缸为研究对象,分别建立工作装置模型、泵控缸液压系统模型以及控制系统模型,并在Matlab/Simulink环境中进行联合仿真。
建模中,由于伺服电机响应远高于液压系统响应,可直接将其视为一个惯性环节[14],并假定电机/发动机效率为95%。
2.1 机械结构模型
在PTC Creo中创建工作装置的三维模型,并导入到Matlab/Simulink得到机械结构模型,如图5所示。

图5 工作装置模型Fig.5 Mechanical model of front attachment of micro-excavator
模型中动臂、斗杆和铲斗的结构尺寸、质量、重心坐标位置分别按照拆解测量的数值来设定,其中液压缸参数见表1。

表1 液压缸参数Tab.1 Parameters of cylinders
2.2 液压系统建模
变转速单泵和双泵控差动缸的液压系统构成基本相同,包括差动液压缸、泵/马达、液压蓄能器和液压管路。建立模型后,根据实际元件的参数和样本资料,分别设置具体参数。
2.2.1油液弹性模量模型
仿真中,采用了简化的Nykänen油液体积弹性模量模型[20-21],其公式为
(9)
式中p0——初始工作压力,Pa
p——当前工作压力,Pa
N——气体多变指数
X0——油液中相对的空气含量
βliq——特定温度下的体积油液弹性模量,Pa
2.2.2液压缸模型
差动缸两端的流体连续性方程为
(10)
(11)
式中ci——液压缸内泄漏系数,m3/(Pa·s)
S——液压缸行程,m
V0A、V0B——液压缸A、B侧的死区容积,m3
QA、QB——液压缸A、B流量,m3/s
pA、pB——液压缸A、B工作压力,Pa
x——活塞位置,m
液压缸负载FL是液压力和粘性摩擦力的合力,即
FL=pAAA-pBAB-Fr-Fend
(12)
式中Fr——粘性摩擦力,N
Fend——终端缓冲力,N
其中,摩擦力Fr采用典型的摩擦力模型(LuGre模型)计算得到,且模型中的参数已通过试验验证,实现摩擦力随着速度而非线性变化[22]。
2.2.3泵/马达模型
由于齿轮泵/马达的泄漏中,仅10%为外泄漏[23],故在此简化了外泄漏,取总泄漏来作为泵/马达的泄漏参数。泵/马达选用可工作于四象限的齿轮马达,如Bosch Rexroth、Hydac、Vivoil等公司的产品;当泵/马达工作在泵和马达工况时,其流量为理论流量减去或加上总泄漏流量,即
(13)
泵/马达的泄漏流量与泵/马达进出口的压差、油液粘度、端面间隙、齿间间隙等相关,考虑到总泄漏流量qLeak与压差基本呈线性关系[24],本文采用与压差和油液粘度相关的泵/马达解析模型为[25]
qLeak=KHPΔp
(14)
其中
式中KHP——Hagen-Poiseuille管中层流系数
ηV,Nom——额定工况(粘度、密度以及角速度)下的容积效率
νNom——额定容积效率下油液运动粘度,m2/s
ρNom——额定容积效率下油液密度,kg/m3
ωNom——额定容积效率下泵角速度,rad/s
ΔpNom——额定容积效率下压力增益,Pa
ρ——油液密度,kg/m2
ν——油液运动粘度,m2/s
Δp——泵/马达的进出口压差,Pa
泵/马达运行在泵和马达工况时,其转矩为
(15)
式(15)中泵/马达的摩擦力矩Tr取决于其进出口压差[25]
Tr=T0+KTP|Δp|
(16)
其中
式中T0——空载时的摩擦力矩,N·m
KTP——压力增益系数
ηTotal——泵/马达的总效率
根据Hydac外啮合齿轮泵的样本进行选型,其中单泵系统采用表2中泵/马达A,而双泵则采用了泵/马达A和B,分别位于液压缸大腔侧和小腔侧。
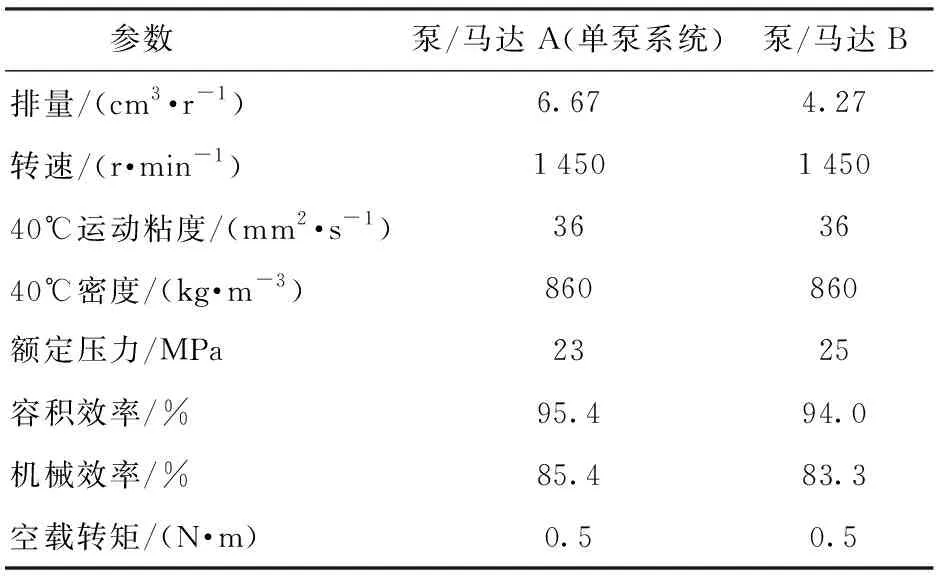
表2 泵/马达模型参数Tab.2 Parameters of pump/motor models
2.2.4液压蓄能器模型
液压蓄能器内理想气体的热力学方程为
(17)
式中V0Acc——液压蓄能器在初始状态下的工作容积,m3
p0Acc——液压蓄能器在初始状态下的压力,Pa
VAcc——蓄能器在工作状态下的容积,m3
pAcc——蓄能器在工作状态下的压力,Pa
将式(17)在工作点附近进行泰勒级数展开,并省略高次项可得
(18)
液压蓄能器的流量为
(19)
2.2.5管路压力损失
将管路部分处视为静态容腔,其内部压力变化为
(20)
式中VH——管路部分容腔总容积,m3
qH1、qH2——管路的进、出流量,m3/s
液压管路损失为
(21)
其中
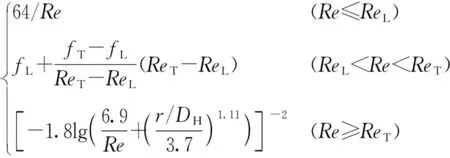
(22)
式中 Δploss——管路压力损失,Pa
q——通过管路的流量,m3/s
Re——雷诺数
ReL——层流时雷诺数
ReT——紊流时雷诺数
fL——临界层流时摩擦因数
fT——临界紊流时摩擦因数
A——管路横截面积,m2
DH——管路水力半径,m
L——管路长度,m
Leq——局部损失等效管路长度,m
r——管路内壁的粗糙度,m
2.2.6能耗和效率模型
系统中液压缸功率PCyl和泵/马达功率PPM分别为
(23)
(24)
取电动机/发电机效率为95%,则在泵工况和马达工况的电动机功率PEM为
(25)
液压缸对外做功ECyl、泵/马达消耗的能量EP和电动机输入能量EEM分别为
(26)
(27)
(28)
液压缸回馈的能量EPo、泵/马达输出的能量EM和电动机输出的能量EGen分别为
(29)
(30)
(31)
液压系统效率ηCyl为液压缸做功ECyl与电机输入能量EEM之比;而势能回收效率ηPo则为电机输出能量EGen与液压缸回馈能量EPo之比,即
(32)
(33)
3 速度开环和闭环控制方法
3.1 速度开环控制
若不考虑系统泄漏、油液压缩和膨胀等因素,则目标速度-电动机转速-液压缸速度之间存在一定的比例关系Kvn(液压缸大腔A和小腔B为控制腔时的增益分别为KA,vn和KB,vn),见表3。

表3 前馈比例增益Tab.3 Proportional gain of feed-forward
2个系统模型的结构和速度开环控制见图6。通过给定速度信号,并经比例放大转换成转速信号,采用矢量控制电动机的转速来调节流量以达到控制液压缸速度的目的。根据表3,可知单泵控制差动缸系统在负载方向改变时,必须采用复杂控制策略来抑制其速度波动,即采用反馈来判断或者预测控制哪一侧为控制腔进而给出相应的增益,本模型中采用两侧的压差ΔpAB=pA-pB来判断控制腔(压力高的一侧为控制腔)。
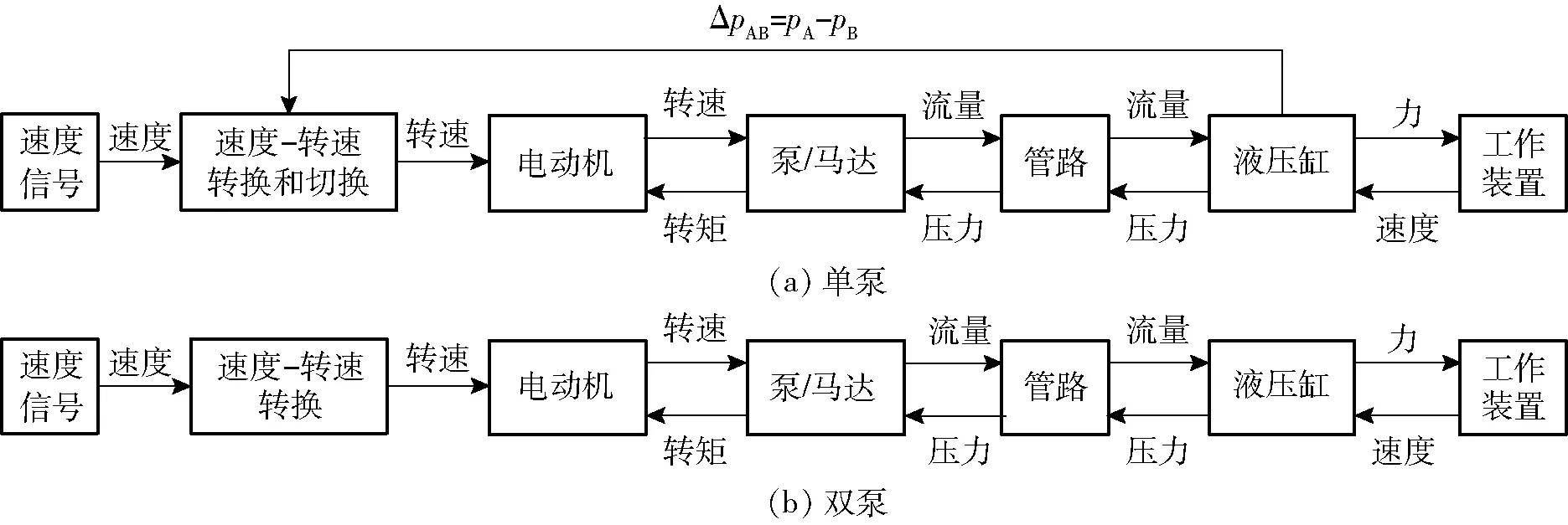
图6 开环控制系统结构图Fig.6 Schematics of open loop velocity control
3.2 速度闭环控制
仅对系统速度开环控制,抗干扰能力差,即速度受外界负载等的波动而波动。因此,对系统进行速度前馈控制的同时,增加速度闭环对速度偏差进行动态补偿实现对速度的精确控制,见图7。

图7 速度前馈和闭环控制系统结构图Fig.7 Schematics of velocity feed-forward and closed loop control
4 液压系统模型验证
为了证明所建立泵控缸液压系统模型的可行性,以单伺服电机驱动双定量泵控差动缸的微型起重机来开展局部验证,其仿真模型如图8所示。所搭建的测试回路和数据采集系统原理如图9所示[26]。在载荷为120 kg,电机输入最高转速为750 r/min的工况下,采用开环控制对液压缸的位移、进出口压力进行测试。将仿真结果与试验结果对比可知,位移和速度曲线基本吻合(图10),但由于试验中的管路相对较长、系统泄漏和油液压缩等,在启动时有一定的滞后。在6~12 s时,由于系统的泄漏(包括液压泵和液压缸内外泄漏),负载有一定的下滑。
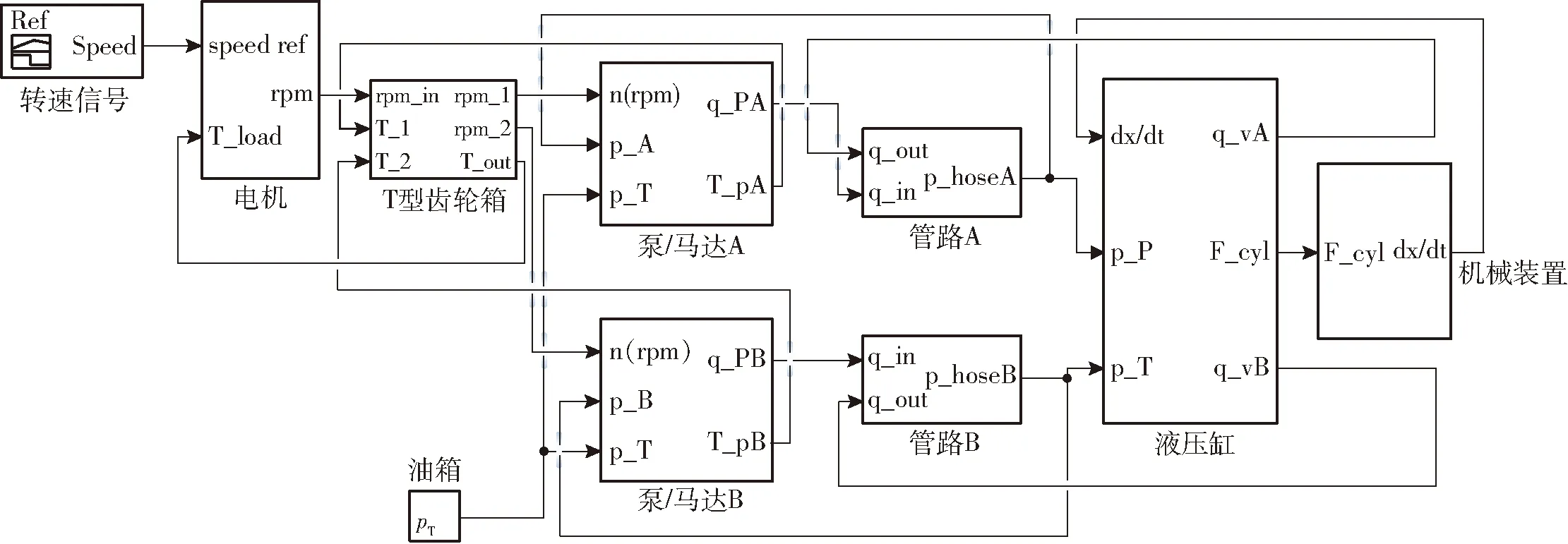
图8 Simulink仿真模型Fig.8 Simulink models
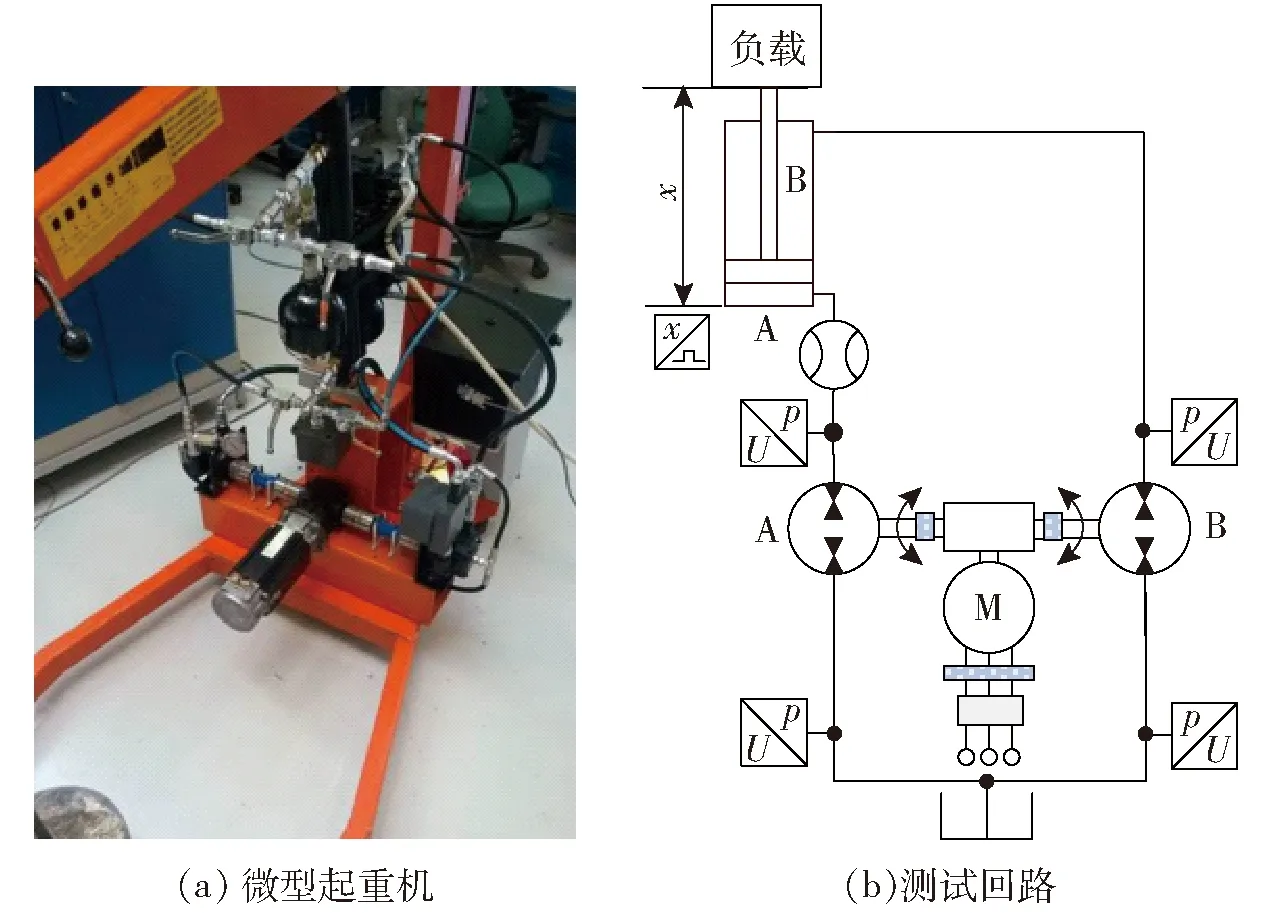
图9 试验现场与测试原理图Fig.9 Picture of experiment and schematic
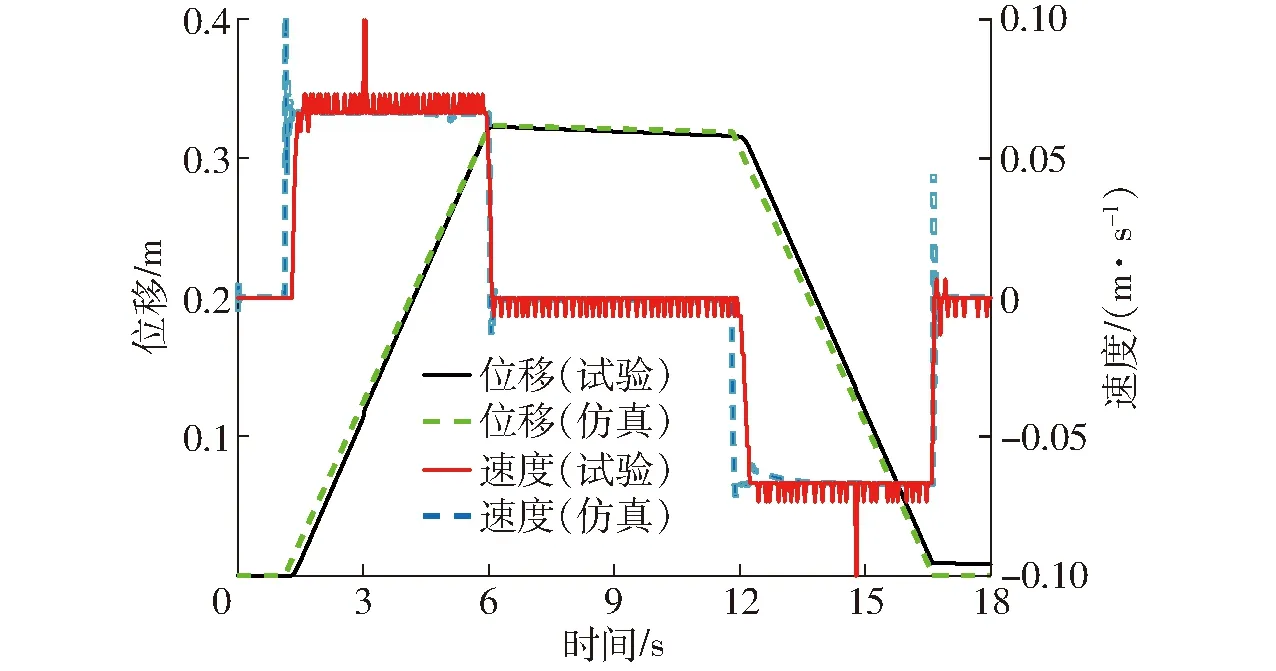
图10 液压缸位移和速度曲线Fig.10 Position and velocity of cylinder
液压缸两腔的压力如图11所示,在液压缸伸出后期(3~6 s),由于液压泵/马达B的排量不足而回油过慢导致液压缸小腔B腔的升力升高,进而使大腔A腔压力升高。由图11可知,仿真压力与测试结果趋势一致,证明了所构建模型用于后续仿真研究是可行的。

图11 液压缸两腔压力曲线Fig.11 Pressure of cylinder chambers A and B
5 仿真结果与分析
在仿真中,斗杆的四象限运行过程如图12所示,斗杆液压缸从0 m处伸出到0.4 m处,再缩回到原来的位置,其中图12c和12e处于负载方向改变过渡阶段。在运行中,保持动臂液压缸和铲斗液压缸锁定,输入零载荷(铲斗为空载)和速度信号给斗杆液压缸(图13a中的参考速度),其中参考位移为参考速度的积分。

图12 挖掘机斗杆四象限工作过程Fig.12 Visualization of four-quadrant operation of stick
5.1 开环控制运行过程及能耗分析
采用图6的控制方法,基于构建的单、双泵系统模型进行仿真,得到如图13所示斗杆四象限工况单双泵控缸开环控制特性。根据工作象限可分成4个阶段来进行特性分析:①阶段1.0~3.3 s中,在斗杆的重力作用下,液压缸负值负载伸出,控制腔为液压缸小腔B,单泵控缸和双泵控缸的速度和位移曲线基本重合。单泵系统速度超调量略大。②阶段3.3~4.5 s,由于斗杆的负载方向变成正值负载,使得控制腔由小腔B切换到大腔A,速度产生了波动;在3.5 s时(a点),单泵系统采用了两侧的压差Δp=pA-pB来判断控制腔,速率误差率为7.1%。而双泵系统的速度误差率仅为2.5%,可见由于负载方向改变引起的控制腔切换导致单泵控缸的速度波动幅度较大,而双泵系统的速度则较稳定。在3.5~4.5 s,由液压缸的液压力近似为零,而两腔压力又很低,控制腔频繁切换,因此速度较不稳定,如单泵系统中4.0 s(b点25.3%)和4.3 s(c点2.4%)的速度波动,双泵系统中速度逐渐降低(误差率由2.5%逐渐升高到7.4%)。③阶段5.6~6.0 s,由于负载方向改变引起的控制腔的切换,再次使单泵和双泵系统的速度出现较大幅度的波动(分别为64.4%和19.8%)。④阶段6.0~9.0 s,单泵系统和双泵系统的速度跟踪性能基本相同。

图13 速度开环控制性能对比Fig.13 Tracking performance comparison with open loop velocity control
单泵系统和双泵系统在中点5 s时的位移误差分别为5、11 mm,在终点10 s处位移误差分别为14、6 mm。可见双泵系统的速度跟踪性能较优。
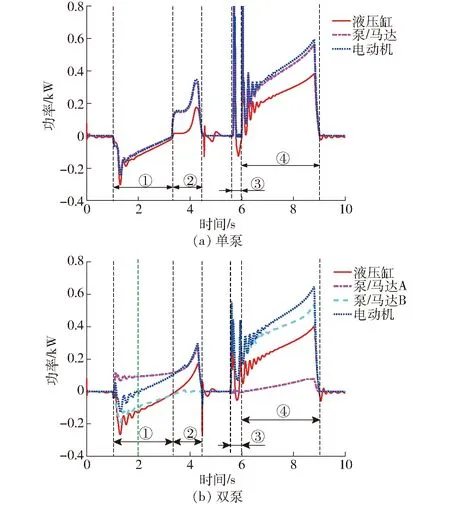
图14 速度开环控制功率曲线Fig.14 Power consumption with open loop velocity control
两个系统的液压缸、泵/马达、电动机的功率分布分别如图14所示。第①阶段1.0~3.3 s中,在负值负载作用下,单泵系统中泵/马达处于马达工况,可通过电动机将回馈的能量转化为电能。而双泵系统中,泵/马达A处于泵工况,存在管路损失、泄漏损失和摩擦损失等。因此虽然泵/马达B运行于马达工况,但电动机仅在1.0~2.0 s可运行于发电工况,一定程度上降低了系统效率,特别是能量回收效率。第②阶段3.3~4.5 s,负载由负切换到正,因此电动机对外做功。单泵系统中,泵/马达运行于泵工况。双泵系统中,泵/马达A运行于泵工况,而泵/马达B基本不做功。第③阶段5.6~6.0 s,由于负载方向的变化,引起工作象限在Ⅲ和Ⅳ中切换,导致速度产生波动,因而电动机的输出功率也产生了一定的冲击。第④阶段6.0~9.0 s,泵/马达A将大腔的液压油增压送到蓄能器另附加泄漏和摩擦损失,需要消耗一定的能量,功率相对单泵系统的略高。由于蓄能器充液过程,压力逐渐升高,损耗的功率逐渐增加。
两个系统的能耗如图15所示,电动机对外做功、泵/马达消耗的能量、液压缸输出能量、液压缸吸收的能量(势能)、泵/马达输出的能量以及可发电的能量分别如表4所示。可知,液压缸对外做功(0.87 kJ和0.89 kJ),而马达吸收的势能则相差较大(0.191 kJ和0.039 kJ),主要是由于双泵系统中大部分势能消耗在驱动泵/马达A上,如图14中的第①阶段1.0~3.3 s所示;因而两个系统的能量回收效率分别为64.3%和15.4%。若不包括再生,单泵系统效率约为59.1%,双泵系统效率约为53.9%。
5.2 速度闭环控制运行过程及能耗分析
采用速度闭环控制后,通过仿真得到如图16所示的速度和位移跟踪特性。在第①阶段开始时,超调量相对开环明显减小。第②阶段,工作象限发生变化时,双泵系统的速度相对较稳定,而单泵系统的则在a点发生波动(误差率为10.9%)。b点和c点则是由系统负载很小,回油背压接近0,使得速度出现较大的波动。在第③阶段时,单泵系统速度误差率最大为11.2%,而双泵的则为5.5%。
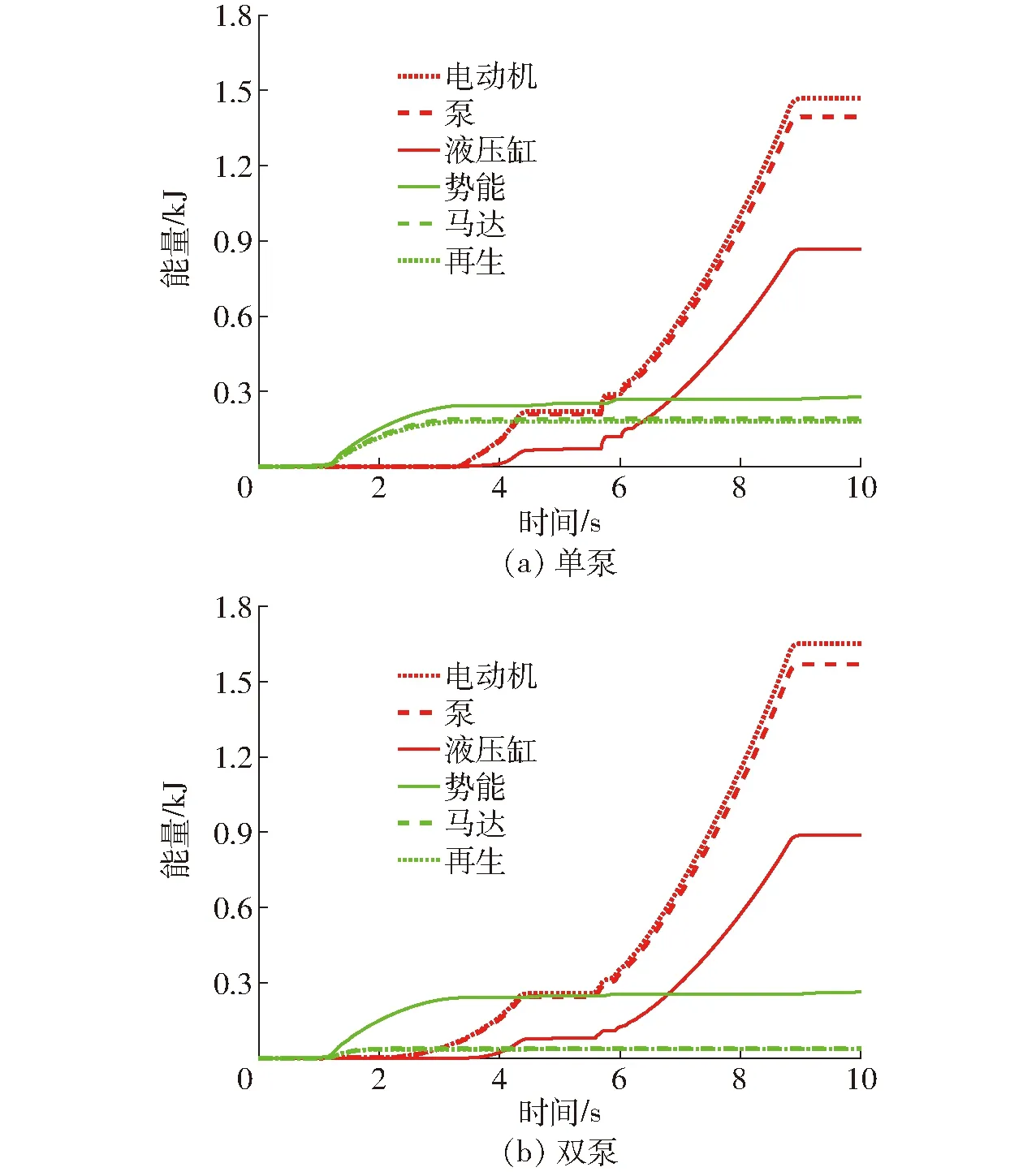
图15 速度开环控制能耗曲线Fig.15 Energy consumption with open loop velocity control
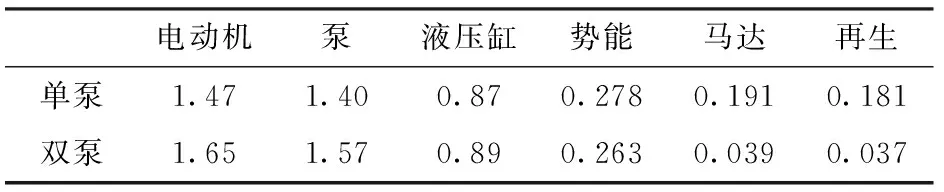
电动机泵液压缸势能马达再生单泵1.471.400.870.2780.1910.181双泵1.651.570.890.2630.0390.037

图16 速度闭环控制性能对比Fig.16 Tracking performance comparison with closed loop velocity control
两个系统在5 s处位移误差为5 mm左右,而10 s处位移误差为4 mm。
由于双泵系统速度闭环控制的各部分功率分布与开环控制系统(图14)相近、能量损耗情况与图15相近,因此在此不再赘述。通过计算得到表5所示速度闭环控制各部分的能耗情况,包括电动机对外做功、泵/马达消耗的能量、液压缸输出能量、液压缸吸收的能量(势能)、泵/马达输出的能量以及可发电的能量。可见,对液压缸外做功均为0.89 kJ、液压缸吸收的势能为0.263、0.252 kJ;但双泵系统由于增加了一个泵/马达而产生泄漏和摩擦损失,因此所需要的输入能量也略有增加,即反馈的势能大部分被消耗在所增加的泵/马达上。不包括再生,单泵系统效率约为56.7%,双泵系统效率约为52.7%。

表5 泵控缸速度闭环控制能耗对比Tab.5 Energy consumption comparison with closed loop velocity control kJ
5.3 对比分析
5.3.1控制性能
根据表6速度开环与速度闭环控制单泵和双泵系统的速度和位移误差进行控制性能对比。
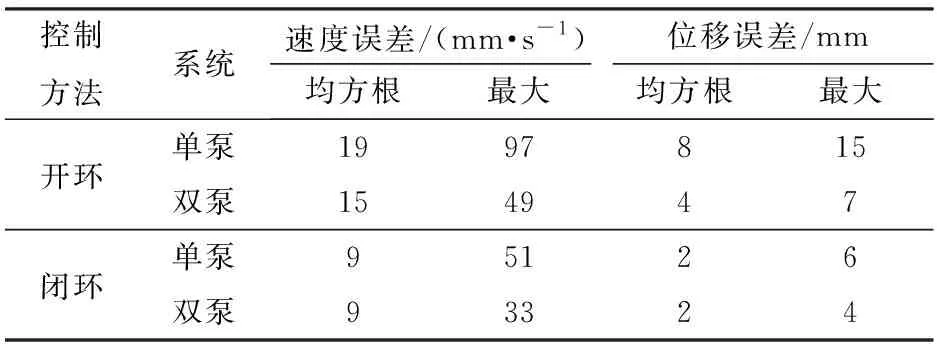
表6 速度开环与速度闭环控制泵控缸系统跟踪误差对比Tab.6 Tracking error comparison of pump controlled cylinder with open or closed loop velocity control
(1)单泵系统与双泵系统
速度开环控制:相对于单泵系统,双泵系统中速度最大误差减少了50%左右,均方根误差约减小了21%;位移最大误差和均方根误差均减小了50%左右。速度闭环控制:相对于单泵系统,双泵系统中速度最大误差减少了35%左右,均方根误差不变;位移最大误差减小了约33%,均方根误差不变。综上所述,双泵系统的速度开环控制和闭环控制性能均明显优于单泵系统。
(2)速度开环与闭环控制
以双泵系统为例,闭环控制速度均方根误差降低了40%,最大误差减小了33%;位移均方根误差降低了50%,最大误差减小了43%。可见由开环到闭环控制的控制性能得到较大幅度提升。
5.3.2能耗和效率
(1)单泵系统与双泵系统
速度开环控制:单泵和双泵系统分别对液压缸外做功约为0.87、0.89 kJ,忽略势能回收,则单泵系统的效率(约59.1%)高于双泵系统的效率(53.9%)。而两个系统的能量回收效率分别为65.1%和14.0%,可知双泵系统的能量回收效率较低,其原因是大部分回馈的势能消耗在所增加泵的泄漏和摩擦上。
速度闭环控制:两个系统对液压缸外做功均为0.89 kJ、液压缸吸收的势能为0.263、0.252 kJ;但双泵系统由于增加了一个泵/马达而产生泄漏和摩擦损失,因此所消耗的能量也略有增加,约增加7.6%。不包括能量回收,单泵系统的效率(56.7%)高于双泵系统的(52.7%)4个百分点。
(2)速度开环与闭环控制
在同一工况下,采用两种控制方法,对外做功基本相同,但效率略有降低,单泵系统由原来的59.1%降低到56.7%,降低2.4个百分点;而双泵系统的效率则由53.9%降低到52.7%,降低1.2个百分点。可知,速度开环和闭环控制的系统效率基本相当。
6 结论
(1)采用速度开环控制或速度闭环控制,双泵系统均消除了四象限工况引起的速度波动,速度控制性能明显优于单泵系统。在开环控制中,双泵系统的速度最大误差较单泵系统的减小了50%,均方根误差减小了21%;在闭环控制中,双泵系统速度最大误差较单泵系统减小了35%,运行0.8 m位移(伸出和缩回各0.4 m)的最大误差仅为4 mm。
(2)速度闭环控制时,双泵系统总效率低于单泵系统(4个百分点)。两种系统均可通过泵/马达带动电动机/发动机发电回收负值负载回馈的能量,但由于双泵系统较单泵系统增加了一个泵所附加的泄漏和摩擦损失,能量回收效率和系统效率略有降低。
(3)在四象限工况下,双泵系统实现了差动缸流量的平衡,消除了四象限工况引起的速度波动问题,同时实现势能和制动能的回收再利用,系统效率最低为52.7%,是一种切实可行的闭式泵控差动缸方案。

