基于PSO-LSSVM的GPS跨河高程拟合研究

李崇伟

(贵阳市测绘院，贵州 贵阳 550018)

1 引 言

现阶段，根据跨河区域地形情况布设合适控制点，采用精密三角高程测量可以进行 2 km～10 km的跨河水准测量。但当跨距大于 10 km时，传统的跨河水准测量方法已经达不到所需精度。此时，可采用GPS水准进行跨河高程传递，而GPS水准法的关键在于获取高程异常值或者高程异常差值，获取的方法有直接计算法和间接拟合法。但是，直接计算法需要大量高精度、分布均匀的重力数据，条件很难满足，所以，实际工程中，较多利用间接拟合的方法。由于模型的差异，产生了很多拟合方法，但在样本数据很少的情况下，这些方法各有缺陷，不能达到很好的拟合效果，为此，本文研究了粒子群优化的最小二乘支持向量机法，并取得了一定效果[9]。

2 基于高程异常差的拟合方法

长距离GPS水准跨河高程传递基于高程异常差的拟合法，可有效解决两岸高程基准不一致的问题。外业测量中，几何水准测量得到的是控制点间的正常高差，而GPS测量后经过基线解也方便得到控制点间大地高差。基于高程异常差的拟合原理就是通过利用两岸已知测段正常高差△h以及由GPS测得的坐标差(△x，△y)、大地高差△H建立模型。建立模型后，即可拟合出跨河测段之间的高程异常差，结合大地高差，计算得到跨河测段正常高差。若跨河测段两端点为I点和J点，两点的水准测量正常高分别为hi、hj，GPS测量大地高分别为Hi、Hj。则有关系式：

(1)

ζj-ζi=Hj-Hi-(hj-hi)

(2)

设△H=Hj-Hi，△h=hj-hi，△ζ=ζj-ζi，则：

△h=△H-△ζ

(3)

式(3)中，△h为正常高高差，△H为大地高高差，△ζ为高程异常差。该原理的思路为：建立基于高程异常差的GPS水准拟合模型，内插求出跨河测段高程异常差△ζ，最后利用△H以及△ζ求出正常高高差△h即可。

3 PSO-LSSVM(粒子群优化的最小二乘支持向量机法)

粒子群优化(PSO)算法，最早是Kennedy等于1995年提出的全局随机优化技术，其基本概念源于对鸟群捕食行为的研究。PSO具有不易陷入局部极小、易实现和调整参数较少的优点，从而用于求解非线性、不可微和多模态问题等。

支持向量机(SVM)是一种新兴的基于结构风险最小化的有效机器学习算法，而最小二乘支持向量机(LSSVM)在继承了SVM优点的同时，还简化了参数，求解非线性问题更加方便。LSSVM已经在似大地水准面的拟合领域取得了较好的效果[7]。

LSSVM拟合高程异常差的思路与神经网络类似[1]，都是通过用两岸的已知数据训练以求出(△x，△y)到△ζ的非线性映射，再仿真跨河段高程异常差。系统选取的核函数为RBF函数，需要确定核函数参数σ以及正则化参数γ，但LSSVM同样没有明确固定的理论指导两个参数的选取。因此，LSSVM法在人为的选定参数上具有很大的随机性和盲目性，导致拟合效果不稳定。为此，本文在前人基础上，在设计GPS跨河高程传递系统时采用PSO-LSSVM，即用PSO(粒子群算法)算法对LSSVM进行参数优化，将得到的最优参数用于训练和仿真拟合得到高精度高程异常差[9]。

4 验证PSO-LSSVM参数的可靠性

LSSVM用于拟合高程异常差时，即使MATLAB有内置的函数用于优化参数，但是参数初始值的设定还是会对拟合的结果产生较大的影响。为了减少对使用者经验的依靠，加入了粒子群优化算法来进行参数的优化选取，本文分别选用LSSVM方法和3组不同初始值的PSO-LSSVM方法进行验证PSO-LSSVM方法参数的可靠性，得到结果如表1、图1所示。

LSSVM与PSO-LSSVM的训练、拟合方差 表1

由表1可以看出，LSSVM法不管是训练的均方差还是拟合的均方差均大于PSO-LSSVM。而且，3组PSO-LSSVM数据的训练、拟合均方差都较为稳定(粒子群算法迭代选择出来的参数也稳定，这里并未列出)，且拟合质量较好。

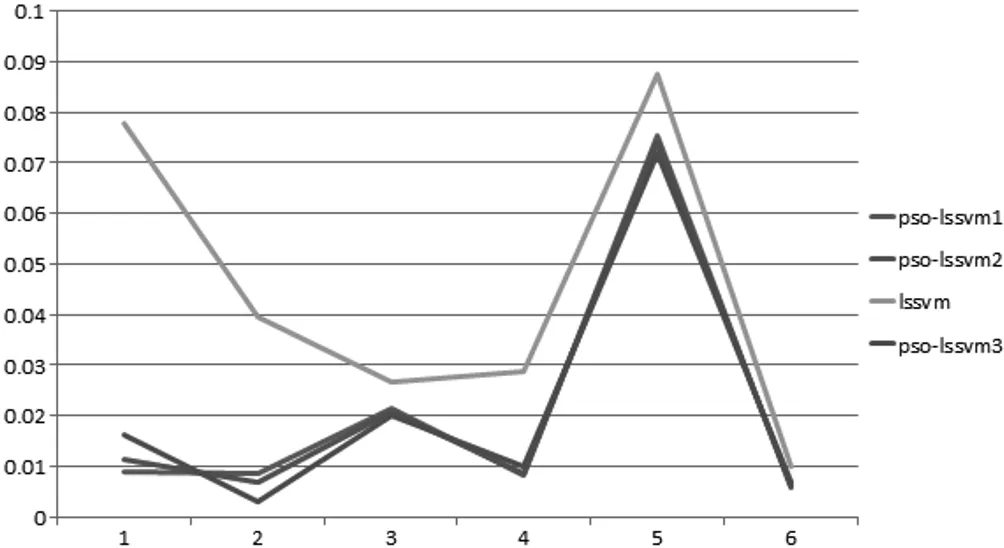
图1 LSSVM与PSO-LSSVM拟合残差比

图1是分别用LSSVM法和PSO-LSSVM法拟合6组跨河测段的结果残差值。6个拟合值中3组PSO-LSSVM法的残差绝对值均要小于LSSVM法。这也从侧面说明，PSO-LSSVM优化参数的性能比LSSVM要好，故其拟合效果也较好，实际的工程实践中，宜选取PSO-LSSVM法(粒子群优化的最小二乘支持向量机法)。

5 工程实例分析

5.1 工程概述

本工程实例西北岸布设有14个C级网控制点，东南岸布设有10个C级网控制点，中间为河流，各点均已经过二等水准联测。跨河基线距离为 22 km～43 km不等，如图2所示。输入原始数据，剔除不良数据，计算待检核跨河测段高差。待检核测段分别为c004-c024、c004-c025、c004-c011、0046-c024、0046-c025、c004-c018、c004-0054、0046-c018、0046-0054。

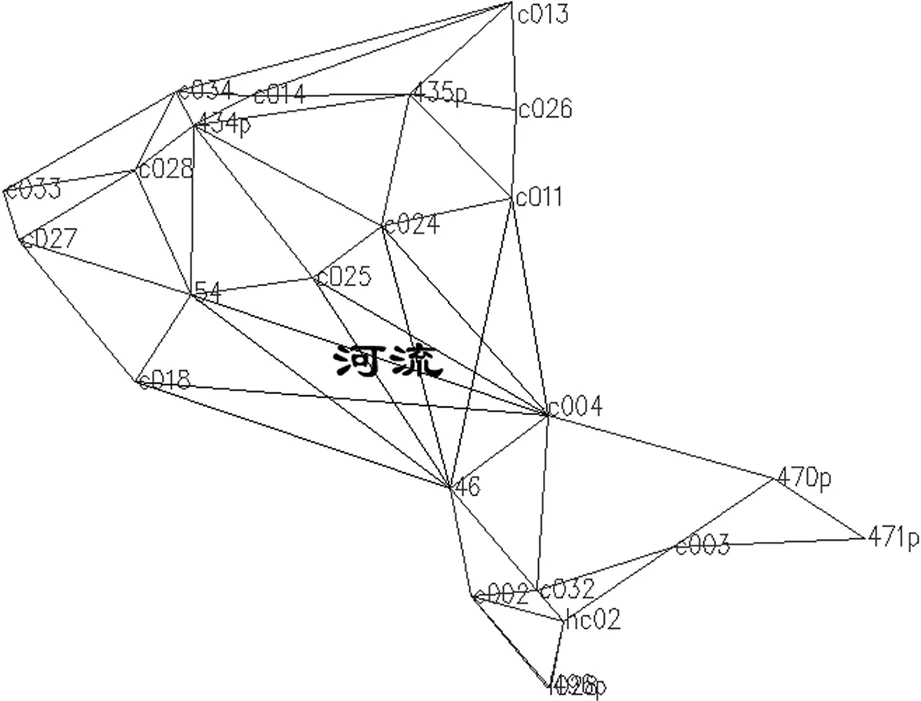
图2 工程实例网型图

5.2 数据对比分析

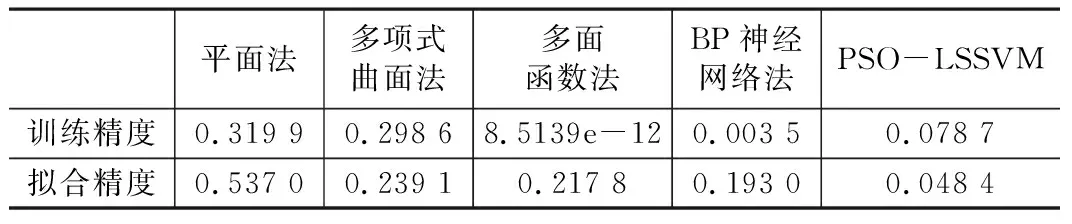
PSO-LSSVM与其他方法内外符合精度对比/m 表2

由表2可得，虽然多面函数法、BP神经网络法训练精度高，但是拟合精度较差。平面法和多项式曲面法拟合检核测段的效果同样不佳，拟合精度低。PSO-LSSVM法拟合精度最高。

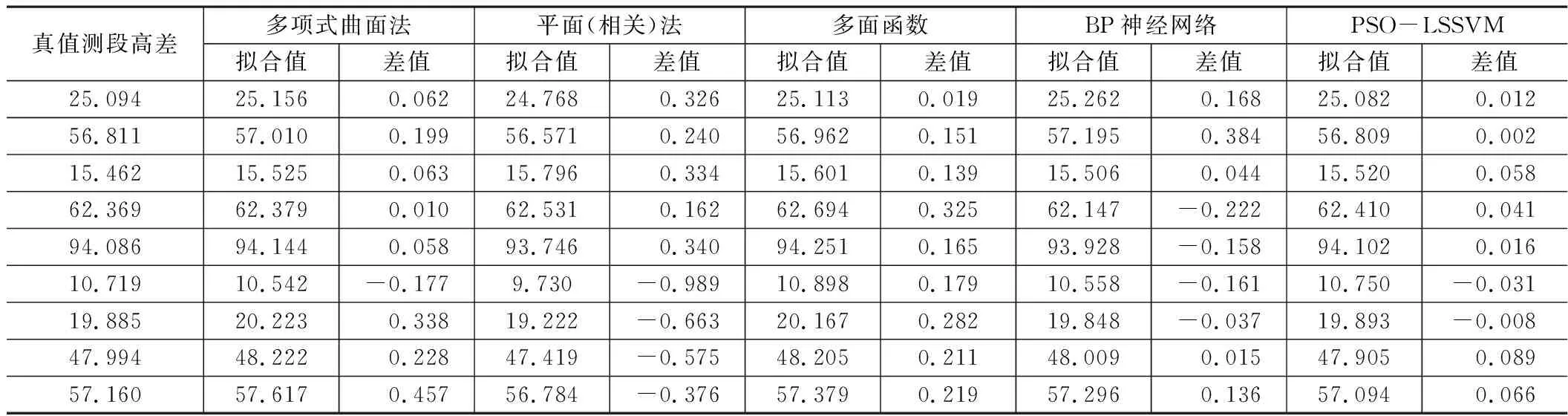
几种方法的跨河测段高差对比/m 表3

由表3可得，平面(相关)模型、多面函数模型、BP神经网络除了个别测段拟合效果较好外，整体拟合效果较差，拟合残差多在十几厘米到几十厘米不等。而多项式曲面模型及PSO-LSSVM整体拟合效果较好，但是后面4个测段，多项式曲面拟合残差较大，必然达不到精度要求。PSO-LSSVM法在所有测段中，最小残差为 0.002 m，最大残差为 0.089 m，是整体拟合效果最好的方法。因此最优结果为PSO-LSSVM(粒子群优化的最小二乘支持向量机法)，其结果符合精度要求，对比限差如表4所示。

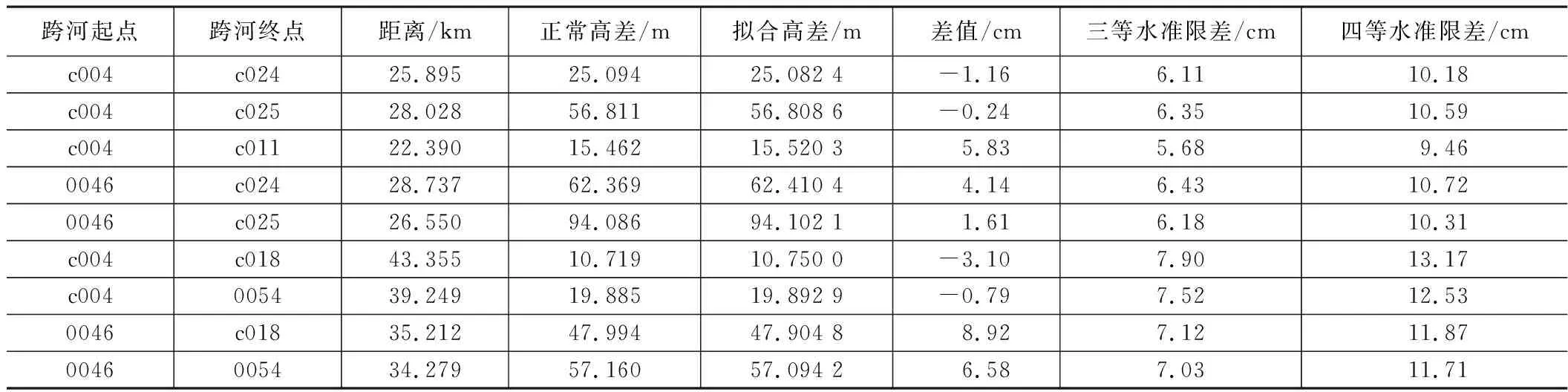
PSO-LSSVM拟合结果 表4

6 结 论

PSO-LSSVM法改善了LSSVM法参数选取的盲目性，保证了参数的稳定性，拟合效果也较稳定。由工程实例分析，跨河距离较长时，PSO-LSSVM法计算结果大部分可以达到四等水准精度，个别也可达到四等精度；平面模型、多项式曲面模型、多面函数模型、BP神经网络法拟合精度较差，无法达到要求。