配筋率及截面尺寸对简支矩形截面钢筋混凝土梁抗爆性能的影响
周清,丁杰,牛宁宁,刘海员
配筋率及截面尺寸对简支矩形截面钢筋混凝土梁抗爆性能的影响
周清,丁杰,牛宁宁,刘海员
滨州市规划设计研究院, 山东 滨州 256600
利用LS-DYNA软件建立了长度为3 m、截面尺寸200 mm×500 mm的简支混凝土梁有限元模型;在跨中梁顶上方布置药量W=10 kg与W=20 kg的2种TNT炸药;分别采用梁整体分析、梁钢筋应力分析、混凝土破坏及塑性变形分析3种分析方法研究了配筋率对爆炸荷载作用下梁抗爆性能的影响。然后,在药量W=20 kg的条件下,保持最大配筋率不变,研究了截面宽度与截面高度的改变对梁抗爆性能的影响。研究发现:(1)与增加纵筋配筋率相比,增加箍筋配筋率能更有效地提高梁的抗爆性能。(2)增加梁截面宽度不利于提高梁抗爆性能。(3)增加梁截面高度能减小梁跨中截面挠度、缩短振动周期、增加梁整体刚度,从而有效地提高梁的抗爆性能。(4)跨中截面梁底纵筋最大应力小于钢筋屈服强度(f=400 MPa),支座处箍筋应力超过钢筋屈服强度。(5)“提高箍筋配筋率+增加梁截面高度”为提高矩形截面梁抗爆性能的最优组合模式。
钢筋混凝土梁; 抗爆性能; 影响因素; 数值分析
有限元软件LS-DYNA被广泛地应用于钢筋混凝土梁抗爆性能研究中[1,2]。李猛深[3]采用LS-DYNA软件对钢筋混凝土梁的抗爆性能进行了研究并与试验结果进行了验证。师燕超[4]借助于LS-DYNA研究了混凝土强度等级、钢筋配筋率等因素对梁抗爆性能的影响。都浩[5]利用LS-DYNA软件建立了简支钢筋混凝土梁的有限元模型,通过与试验结果进行对比验证了数值分析的准确性并对爆炸荷载作用下梁的破坏形态进行了分析。
笔者在总结以往学者成果的基础上,对以下3方面进行了进一步改进;并在此基础上研究了配筋率、截面宽度、截面高度等各因素对梁抗爆性能的影响。
(1)部分学者所建立梁有限元模型与实际梁存在一定偏差。结构设计中,简支梁最常用长度为3~6 m,配筋率约为1%~2%。笔者所建立简支梁有限元模型长度为3 m,配筋率在1%~2%取值。
(2)学者多采用跨中最大挠度做为评估梁抗爆性能的参数。笔者根据简支梁的受力特点,除采用跨中最大挠度外,增加了梁整体振动曲线、梁振动周期、纵筋应力、支座箍筋应力、钢筋利用率等多项指标评估梁的抗爆性能。
(3)LS-DYNA软件较难模拟混凝土的破坏情况,笔者通过增加删除混凝土的单元关键字*MAT_ADD_EROSION配合观察梁顶混凝土的塑性应变情况来判定混凝土的损伤与破坏。
1 有限元模型与荷载的施加
1.1 有限元模型
LS-DYNA所有的混凝土材料模型中,*MAT_CONCRETE_DAMAGE最能有效地模拟混凝土在高应变、大变形下的力学形态。*MAT_CONCRETE_DAMAGE _REL3模型为*MAT_CONCRETE_DAMAGE的升级版本,在保留了后者优点的同时,在模型参数的确定方面做了简化,使用此模型模拟混凝土材料,用户仅需要定义几个常用的基本参数。笔者采用该模型模拟C40混凝土,其具体参数见表1。
采用弹塑性模型*MAT_PLASTIC_KINEMATIC模拟HRB400钢筋,其具体参数见表2。

表 1 C40混凝土模型参数
备注:表示密度;为弹性模量;为泊松比;f和f分别为C40混凝土的抗压强度和抗拉强度
Note:is density;is elasticity modulus;is Poisson ratio;fandfare the compressive strength and tensile strength of C40 concrete respectively.

表 2 HRB400钢筋模型参数
备注:表示密度;f为屈服应力;为硬化参数;和tan分别为弹性模型和切线模量;、为Cowper-Symonds应变率参数;为失效应变。
Note:is density;fis yield stress;is hardening parameter;andtanare the elasticity modulus and tangent modulus;,are the Cowper-Symonds strain rate parameters;is failure strain.
混凝土采用SOLID164单元,钢筋采用BEAM161单元。根据众多学者的数值模拟经验[6-8],爆炸超压作用时间很短,可以忽略钢筋与混凝土之间的相对滑移,故采用共用节点的方式定义两者之间的接触。钢筋与混凝土有限元网格尺寸均为15 mm。
爆炸荷载作用下,混凝土会发生损伤甚至破环。LS-DYNA中,各混凝土材料模型较难直观地观察到裂缝及破环情况。笔者采用以下方法加以解决:(1)爆炸荷载作用下,梁顶截面受压破坏通过观察混凝土材料的塑性应变发展情况加以评价。(2)爆炸荷载作用下,跨中梁底混凝土受拉、支座混凝土受剪破坏通过添加关键字*MAT_ADD_EROSION、观察单元删除情况加以评价。
1.2 材料应变率效应
爆炸荷载作用下,材料的应变率可高达1000 s-1,钢筋与混凝土的强度会有较大程度的提高[9,10]。在近距离抗爆数值模拟时通常采用动力增大系数(Dynamic increase factor)来考虑材料的应变率效应。定义为某一应变率下材料的动力强度与静力强度之比。混凝土的动力强度增大系数采用欧洲(CEB)提出的混凝土动力强度增大公式与应变率关系模型。依据规范规定,混凝土抗压强度的动力强度增大公式的计算公式为:

上式中,=σ/σ,其中σ为某一应变率下的动态压缩强度;σ为静态压缩强度;
ε=0.00003/s (2)
=(5+3σ/4),σ表示混凝土立方体抗压强度,单位为MPa;
lg()=6.156-0.49 (3)
应变率在10/s~100/s范围内,欧洲(CEB)混凝土抗拉强度的动力强度增大公式的计算公式为:

上式中,=σ/σ,其中σ为某一应变率下的动态拉伸强度;σ为应变率ε=0.00003/s下的静态拉伸强度。的应用范围为0.00003/s~300/s;
lg()=7.112.33 (5)
上式中,=1/(10+6σ/σ0);σ为静态压缩强度,σ0是数值为10 Mpa的参考值。
钢筋的动态强度增大系数的计算公式为:
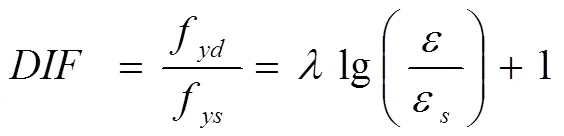
上式中,=0.03;ε为材料的静力应变率,ε=100/s;f为钢筋的动力屈服强度;f为钢筋的静力屈服强度。
1.3 爆炸荷载与重力荷载的施加
利用LS-DYNA关键字*LOAD_BLAST_ENHANCED配合关键字*LOAD_SEGMEMT_SET定义爆炸荷载[11]。标准TNT炸药会产生很大的超压荷载而对结构构件造成严重的破坏。笔者根据以往学者的研究成果[12],选择W=10 kg(产生较小荷载)与W=20 kg(产生较大荷载)两种药量。该药量既保证了梁能够发生破坏而又不至发生完全破坏。
利用LS-DYNA关键字*DEFINE_CURVE配合关键字*LOAD_BODY_Y定义梁竖直方向的重力,重力加速度取值9.81 m/s2。

图 1 素混凝土梁尺寸及爆炸点位置示意图
2 素混凝土梁在爆炸荷载作用下的破坏形态
素混凝土梁长度为3 m,截面尺寸为200 mm×500 mm,爆炸点位于跨中截面正上方1 m(图1)。
通过观察图2可以看出,药量W=10 kg时,梁发生破坏,梁截面中部出现较大裂缝,支座发生严重破坏。通过观察图3可以看出,药量W=20 kg时,梁破坏程度较药量W=10 kg时更加严重,梁截面中部裂缝扩展为较大的空洞,梁以空洞为界断为2段。梁支座发生完全破坏。图4为利用LS-DYNA软件采集到的梁整体变形图。素混凝土梁在2种药量的爆炸荷载下均发生完全破坏。药量越大,其时间-竖向位移曲线斜率越大,破坏程度越大。

图 2 药量10 kg时,素混凝土梁被破坏状态

图 3 药量20 kg时,素混凝土梁被破坏状态

图 4 素混凝土梁时间-竖向位移曲线

图 5 钢筋混凝土梁尺寸及爆炸点位置示意图
3 配筋率对梁抗爆性能的影响
3.1 截面尺寸及配筋方案
钢筋混凝土梁长度为3 m,截面尺寸为200 mm×500 mm,爆炸点位于跨中截面正上方1 m。


表 3 纵筋配筋方案
备注:梁有效高度按照465 mm(即as=35 mm)取值;纵筋配筋率按照=As/(bh0)计算;箍筋面积配箍率按照SV=nAs/(bs)计算
Note: The effective height is as high as 465 mm(as=35 mm); Longitudinal reinforcement ratio is calculated as=As/(bh0); Stirrup ratio is calculated asSV=nAs/(bs).

表 4 箍筋配筋方案
3.2 梁整体振动分析
图6~9分别表示药量W=10 kg、W=20 kg,不同配筋方案梁的整体时间-竖向位移振动曲线,通过分析可以得到以下结论:(1)药量越大,梁竖向挠度越大、振动周期越长、刚度越小、抗爆性能越差。(2)增大纵筋配筋率、箍筋配筋率均可提高梁的抗爆性能,药量越大作用越明显。(3)增大箍筋配筋率对梁抗爆性能的提高程度优于增大纵筋配筋率。以图7、图9为例,方案4较方案2挠度减小仅1 mm,周期减小约5 ms;而方案6较方案2挠度减小5 mm,周期减小约10 ms。

图 6 药量W=10 kg,不同纵筋配筋率梁的时间-竖向位移曲线

图 7 药量W=20 kg,不同纵筋配筋率梁的时间-竖向位移曲线

图 8 药量W=10 kg,不同箍筋配筋率梁的整体时间-竖向位移曲线

图 9 药量W=20 kg,不同箍筋配筋率梁的整体时间-竖向位移曲线
3.3 钢筋应力分析
通过对梁钢筋应力汇总表5分析可以得到以下结论:(1)爆炸荷载作用下梁底混凝土会发生脱落而使得梁底纵筋没有屈服而退出工作,梁底钢筋不能充分发挥作用。药量W=10 kg,钢筋纵筋配筋率由0.82%增大为1.58%,梁底纵筋利用率由40%减小为23%;药量W=20 kg,钢筋纵筋配筋率由0.82%增大为1.58%,梁底纵筋利用率由64.5%减小为32%。以上说明,随着纵筋配筋率的增大,梁底纵筋利用率降低。并且药量越大,降低程度越大。(2)无论药量W=10 kg或W=20 kg,支座箍筋应力均超过钢筋屈服强度。箍筋应力值在各工况下均较为稳定,约为600 MPa左右。(3)增大箍筋配筋率会增加混凝土的约束作用,从而使得梁底纵筋钢筋利用率有所提高。药量W=10 kg时,方案2与方案6的纵筋配筋不变,当箍筋配筋率由0.505%增大为1.130%时,相应的纵筋利用率由33.5%增大为45%。药量W=20 kg时情况相同。

表 5 梁钢筋应力汇总表
备注:钢筋应力利用率按照(钢筋实际应力/钢筋屈服应力)×100%计算,钢筋屈服应力取值400 MPa。
Note: The reinforcement stress utilization is calculated as (actual stress/yield stress) ×100%, reinforcement yield stress is 400 MPa.
3.4 混凝土破坏程度分析

图 10 药量W=20 kg,纵筋配筋率最大时,梁破坏图与混凝土塑性应变图

图 11 药量W=20 kg,箍筋配筋率最大时,梁破坏图与混凝土塑性应变图
图10、图11分别表示药量W=20 kg,纵筋配筋率、箍筋配筋率最大时,梁破坏图与混凝土塑性应变分布图。通过分析可以得到以下结论:(1)纵筋配筋、箍筋配筋率最大时,梁破坏区、混凝土塑性应变区位置基本一致。(2)跨中梁底截面混凝土以弯曲破坏为主,而支座处混凝土以剪切破坏为主。(3)梁顶混凝土塑性区域主要分布在爆炸点附近与梁支座。
4 截面宽度对梁抗爆性能的影响
通过上文研究发现,梁的抗爆性能在配筋率最大时表现最明显。所以,研究截面宽度对梁抗爆性能影响时,配筋方案分别取纵筋面积最大的配筋方案4与箍筋面积最大的配筋方案6。梁截面宽度取200 mm、250 mm、300 mm共3种,其在2中配筋方案下的6种截面形式如图12所示。

图 12 不同梁宽、最大纵筋与箍筋配筋率下,梁的6种截面形式
4.1 梁整体振动分析
梁截面宽度增大会对梁的抗爆性能产生2方面的影响:(1)使梁接触爆炸荷载的面积增大。(2)使梁整体刚度增强。梁抗爆性能应为上述2方面影响的综合结果。
图13表示药量W=20 kg,纵筋配筋率、箍筋配筋率最大时,不同梁宽的梁整体时间-竖向位移曲线。通过分析可以得到以下结论:(1)纵筋配筋率不变时,采用方案3的梁跨中挠度约较方案1增大4 mm。箍筋配筋率不变时,采用方案6的梁跨中挠度较方案4增大4 mm。(2)随着梁截面宽度的增加,梁整体振动周期变长。
以上说明,梁截面宽度越大,梁竖向挠度越大,周期越长,破坏程度越大。

图 13 药量W=20 kg、纵筋配筋率最大,不同梁宽的时间-竖向位移曲线
4.2 钢筋应力分析

表 6 梁钢筋应力汇总表
通过对梁钢筋应力汇总表6分析可以得到以下结论:(1)跨中纵筋应力均未超过钢筋屈服强度。随着截面宽度增加,纵筋钢筋应力增大。(2)支座箍筋应力均超过屈服强度。随着截面宽度增加,箍筋应力变化不大,约为600 MPa。
4.3 混凝土破坏程度分析
图14、图15分别表示药量W=20 kg,纵筋配筋率、箍筋配筋率最大时,b=300 mm的梁破坏图与混凝土塑性应变分布图。通过分析可以得到以下结论:(1)纵筋与箍筋配筋率最大时,梁破坏区主要分布在梁底与支座。梁底部分混凝土脱离梁主体,支座出现大量斜裂缝。与上文图10、图11相比,破坏程度更加严重。(2)梁顶截面塑性区域主要分布在爆炸点正对截面附近与支座。与上文图10、图11相比,梁塑性区域增大,梁顶混凝土塑性破坏更加严重。

图 14 药量W=20 kg、纵筋配筋率最大、梁宽b=300 mm时,梁破坏图与混凝土塑性应变图

图 15 药量W=20 kg、箍筋配筋率最大、梁宽b=300 mm时,梁破坏图与混凝土塑性应变分布图
5 截面高度对梁抗爆性能的影响
与上文所采用的方法相同,研究截面高度对梁抗爆性能影响时,配筋方案分别取纵筋面积最大的配筋方案4与箍筋面积最大的配筋方案6。梁截面高度取500 mm、600 mm、700 mm共3种,其在2中配筋方案下的6种截面形式如图16所示。

图 16 不同梁高、最大纵筋与箍筋配筋率下,梁的6种截面形式
5.1 梁整体振动分析
图17、图18分别表示药量W=20 kg,纵筋配筋率、箍筋配筋率最大时,不同梁高的梁整体时间-竖向位移曲线。通过分析可以得到以下结论:(1)纵筋不变时,梁截面高度由500 mm增加至700 mm,梁竖向挠度由11 mm减小为3 mm。箍筋不变时,梁截面高度由500 mm增加至700 mm,梁竖向挠度由8 mm减小为2 mm。(2)纵筋、箍筋不变时,采用截面3、截面6的梁振动周期较采用截面1、截面4明显缩短,刚度明显增强。采用截面6的梁振动周期最短,振动图形最稳定,抗爆性能最好。
以上说明,在保持最大纵筋配筋率、最大箍筋配筋率不变的条件下,增大梁截面的高度可以有效地提高梁抗爆性能。
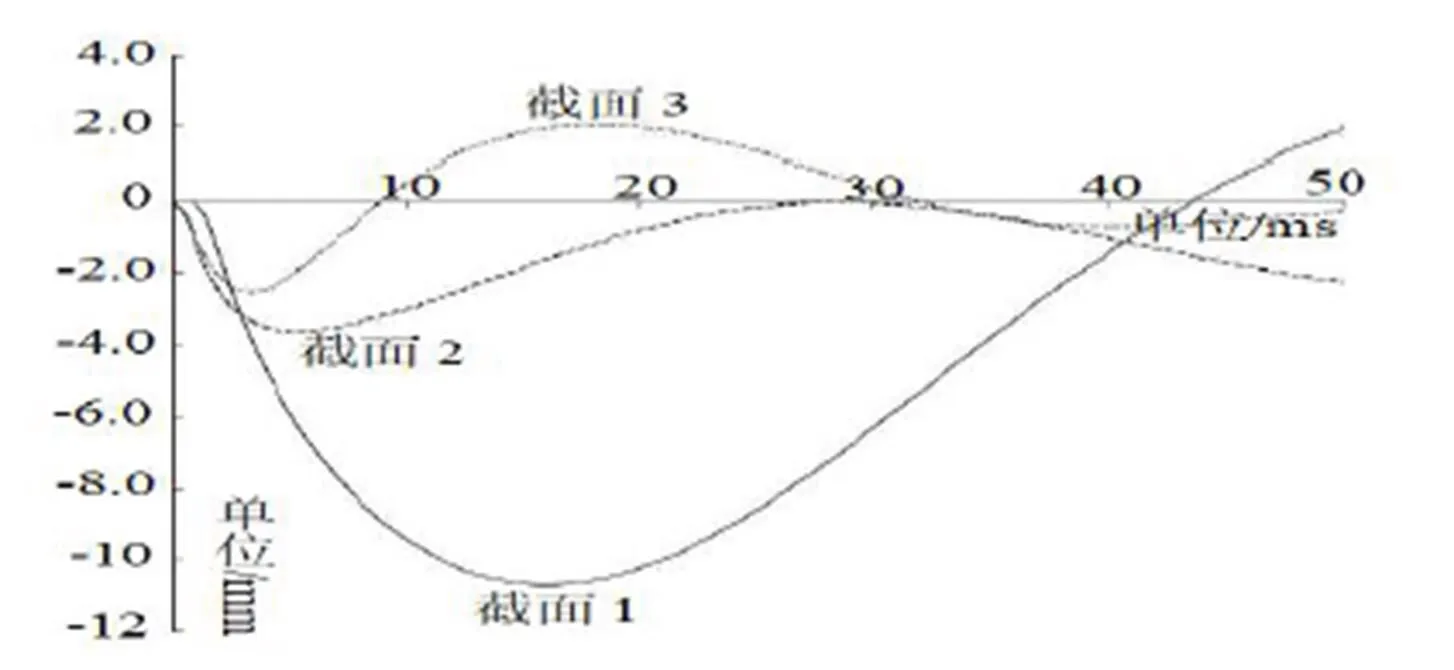
图 17 药量W=20 kg、纵筋配筋率最大,不同梁高的整体时间-竖向位移曲线

图 18 药量W=20 kg、箍筋配筋率最大,不同梁高的整体时间-竖向位移曲线
5.2 钢筋应力分析

表 7 梁钢筋应力汇总表
通过对梁钢筋应力汇总表7分析可以得到以下结论:(1)跨中纵筋应力均未超过钢筋屈服强度。随着截面高度增加,纵筋钢筋应力增大,利用率提高。(2)支座箍筋应力均超过屈服强度。随着截面高度增加,箍筋应力变化不大,在600 MPa上下浮动。
5.3 混凝土破坏程度分析
图19、图20分别表示药量W=20 kg,纵筋配筋率、箍筋配筋率最大时,h=700 mm的梁破坏图与混凝土塑性应变分布图。通过分析可以得到以下结论:(1)纵筋与箍筋配筋率最大时,梁破坏区主要分布在梁底与支座。与图14、图15相比,梁底混凝土没有脱离梁主体;同时,支座出现斜裂缝较少。(2)梁顶截面塑性区域主要分布在爆炸点正对截面附近与支座。与图14、图15相比,梁混凝土塑性区域变小、颜色变浅,说明混凝土塑性破坏程度较小。

图 19 药量W=20 kg、纵筋配筋率最大、梁高h=700 mm时,梁破坏图与混凝土塑性应变图

图 20 药量W=20 kg、箍筋配筋率最大、梁高h=700 mm时,梁破坏图与混凝土塑性应变分布图
6 结论与建议
在以往学者研究的基础上,利用LS-DYNA软件,对影响矩形截面钢筋混凝土简支梁抗爆性能的因素进行了详细的分析。通过研究发现:
(1)爆炸荷载作用下,素混凝土梁发生严重的破坏。即使药量很小(W=10 kg),梁破坏程度仍非常严重。
(2)增大纵筋配筋率与箍筋配筋率均能够提高梁的抗爆性能。相同条件下,增大箍筋配筋率较增大纵筋配筋率效果更好。
(3)增大截面宽度虽然一定程度上增加了梁的整体刚度,当同时增加了爆炸荷载作用面积。综合分析,增大梁截面宽度不利于提高梁的抗爆性能。
(4)增大梁的截面高度会较大程度地减小爆炸荷载作用下梁跨中截面的挠度,使梁振动周期变短、刚度增加,从而有效地提高了梁的抗爆性能。
(5)跨中梁底纵筋应力一般均小于钢筋屈服强度,而支座箍筋应力均超过钢筋屈服强度且在各种工况下应力值较为稳定。
(6)“增加梁截面高度+提高箍筋配筋率”为提高简支矩形截面钢筋混凝土梁抗爆性能的最优组合形式。
[1] 刘成清,何斌,陈弛,等.ANSYS/LS-DYNA工程结构抗震、抗撞击与连续倒塌分析[M].北京:中国建筑工业出版社,2014
[2] 唐长刚.LS-DYNA有限元分析及仿真[M].北京:电子工业出版社,2014
[3] 李猛深,李杰,李宏,等.爆炸荷载下钢筋混凝土梁的变形和破坏[J].爆炸与冲击,2015,35(2):177-183
[4] 李忠献,师燕超.建筑结构抗爆分析理论[M].北京:科学出版社,2015
[5] 都浩,邓芃,杜荣强.爆炸荷载作用下钢筋混凝土梁动力响应的数值分析[J].山东科技大学学报:自然科学版,2010,29(6):50-54
[6] 田力,付协伟.爆炸荷载作用下高层钢筋混凝土框架结构的连续倒塌机理研究[J].科学技术与工程,2016,16(3):232-238
[7] 师燕超,李忠献,郝洪.爆炸荷载作用下钢筋混凝土框架的连续倒塌分析[J].解放军理工大学学报,2007,8(6):652-658
[8] 周清,牛宁宁,刘海员,等.剪跨比对爆炸荷载作用下钢筋混凝土梁抗爆性能及破坏形态的影响[J].水利与建筑工程 学报,2017,15(1):219-224
[9] Bischoff PH, Perry SH. Compressive behavior of concrete at high stain rate[J]. Material and Structure, 1991,24(144):425-450
[10] Malvar L. Review of static and dynamic properties of steel reinforcing bars[J]. ACI Material Journal, 1998,95(5):609-616
[11] 李忠献,师燕超,史祥生.爆炸荷载下钢筋混凝土板破坏评定方法[J].建筑结构学报,2009,30(6):60-66
[12] 汪维,刘瑞朝,吴飚,等.爆炸荷载作用下钢筋混凝土梁毁伤判据研究[J].兵工学报,2016,37(8):1421-1429
Influence of Reinforcement Ratio and Section Size on the Anti-explosion Performance of RC-beam with Rectangular Section
ZHOU Qing, DING Jie, NIU Ning-ning, LIU Hai-yuan
256600,
The finite element model of simply supported concrete beam with the length of 3m and the section of 200 mm×500 mm is established by LS-DYNA software. Two kinds of TNT explosives, W=10 kg and W=20 kg, are arranged on the top of the middle span beam. The influence of reinforcement ratio on the anti-explosion performance of beams under explosive load action was studied by three analysis methods: beam integral analysis, beam reinforcement stress analysis, concrete failure analysis and plastic deformation analysis. Then, the influence of changing section width and section length on the anti-explosion performance was studied under the condition of W=20 kg dosage and the constant maximum reinforcement ratio, the study found that (1) Compared with the increasing longitudinal reinforcement ratio, increasing the ratio of stirrup reinforcement can improve the beam anti-explosion performance more effectively. (2) Increasing the width of beam is not conductive to improving the beam anti-explosion performance. (3) Increasing the height of the beam section can reduce the deflection of the middle section, shorten the vibration period and increase the overall stiffness of the beam, and improve the anti-explosion performance of the beam effectively. (4) The maximum stress of longitudinal reinforcement at the bottom of the mid-span beam is less than the yield strength of the steel bar (fy=400 MPa) and the stirrup stress at the support exceeds the yield strength of the steel bar. (5) "Increasing stirrup reinforcement ratio + increasing beam section height" is the optimal combination mode to improve the anti-explosion performance of rectangular cross-section beam.
RC-beam; anti-explosion performance; influence factor; numerical analysis
[TU352.1+3]
A
1000-2324(2018)06-1024-08
10.3969/j.issn.1000-2324.2018.06.024
2017-05-25
2017-08-14
山东省住房和城乡建设厅科学技术计划项目(2017-K4-007)
周清(1982-),男,硕士,高级工程师.主要从事结构设计工作及工程结构抗爆研究. E-mail:zhouqingtianda@163.com

