采用不等长缓和曲线优化站端小半径曲线的探讨
吕昌明
(中铁第一勘察设计院集团有限公司,陕西 西安 710043)
地铁作为运量大、速度快的轨道交通项目在各个城市相继建设。因城市空间关系复杂,地铁车站位置通常要考虑线路走向、客流集散点分布、换乘关系等因素,设置受限,特殊情况下会出现站端小半径曲线的情形。目前站端小半径曲线通常采用等长缓和曲线加圆曲线,但该设计方案半径小,限速大,轮轨磨耗严重。针对这些问题,本文提出采用不等长缓和曲线优化站端小半径曲线的方案,并在此基础上探讨轨道超高设置、限速等问题。
1 站端小半径曲线及不等长缓和曲线
1.1 站端小半径曲线
根据小半径曲线在线路平面中的位置,分为区间小半径曲线和站端小半径曲线。前者一般因线路转换路由、绕避控制因素等情况采用,后者一般因车站位置受限、绕避站端控制因素、避免缓和曲线侵入有效站台等情况采用。设计中,缓和曲线长度依据GB 50157—2013《地铁设计规范》[1]中的“线路曲线超高—缓和曲线长度”表,针对不同的圆曲线半径进行取值。通常半径不大于350 m的圆曲线被定义为小半径曲线,或者根据速度目标值的大小确定小半径曲线标准。
1.2 不等长缓和曲线
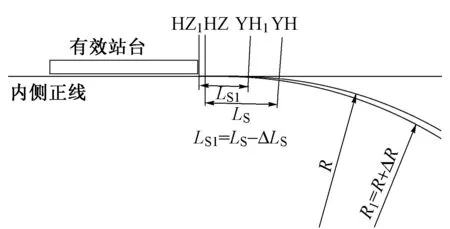
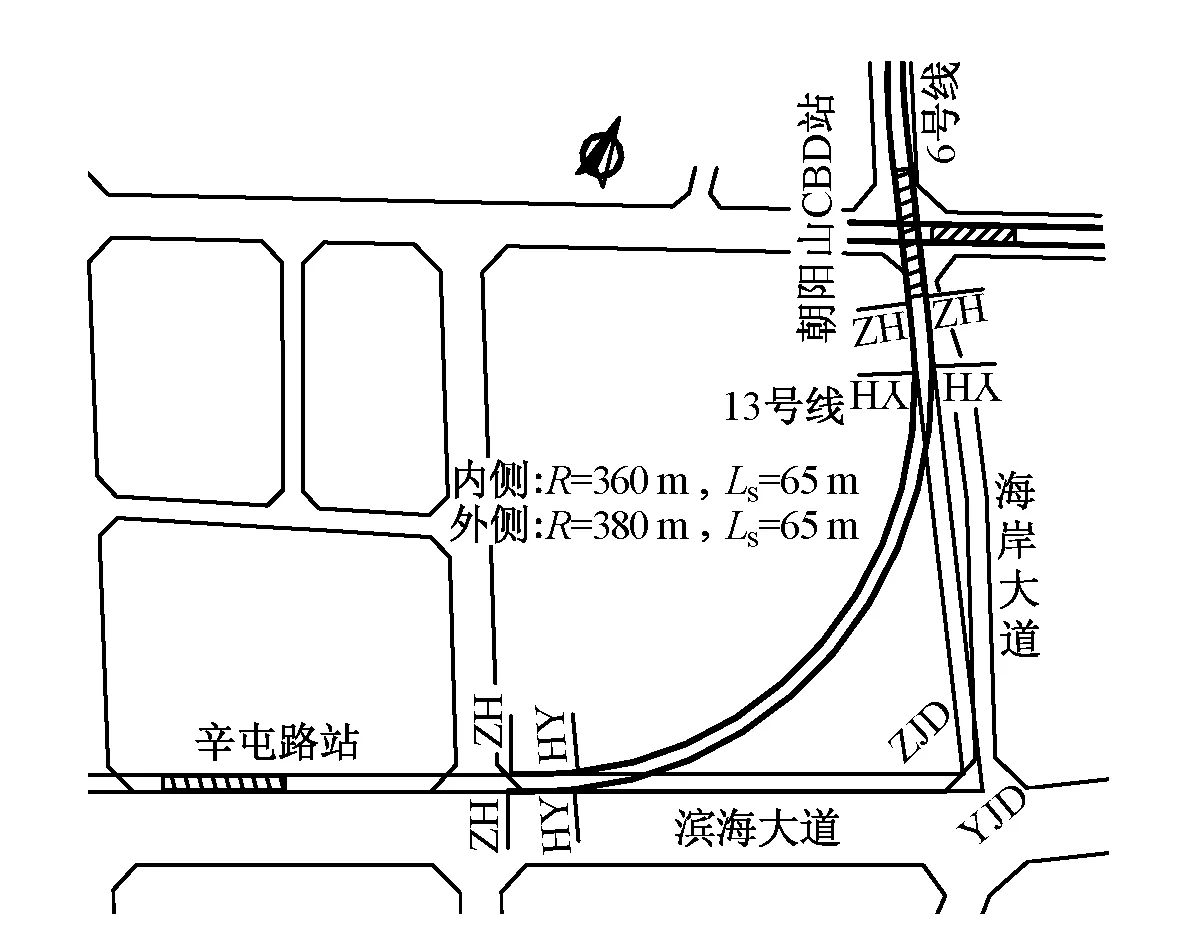
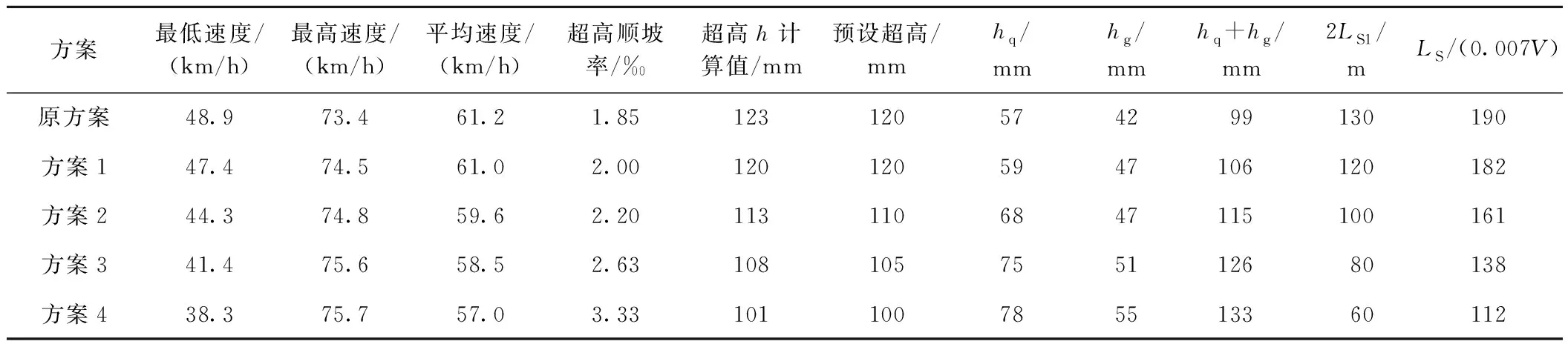
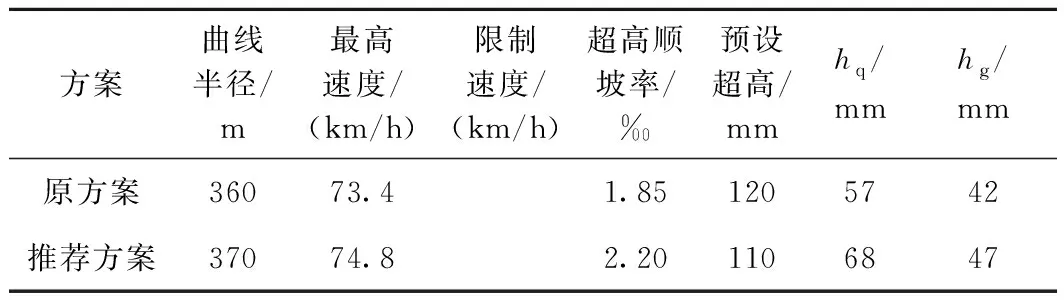
不等长缓和曲线,即圆曲线两侧的缓和曲线长度不相等,内移距也不相等,曲中点不在曲线转点的分角线上,而是偏向较短缓和曲线的一侧[2],缓和曲线短的一侧对应的切线短。图1为不等长缓和曲线,其中LS1 图1 不等长缓和曲线 线路出有效站台后,接半径为R、缓和曲线长度为LS的曲线,两端缓和曲线长度L1,L2相等,即L1=L2=LS。近站端直缓点HZ与有效站台端部距离较近,但未侵入有效站台。另一端缓和曲线条件不受限,不进行讨论。 图2 不等长缓和曲线优化示意 取内侧正线进行不等长缓和曲线优化,如图2所示。优化方法具体为:半径R增大ΔR(地下线ΔR一般可取5 m的整倍数),调整为R1,R1=R+ΔR。为保证曲线不进有效站台,近站端缓和曲线长度必然减小,此时LS减少ΔLS,调整为LS1,LS1=LS-ΔLS。该方法较简单,即增大曲线半径,减少近站端缓和曲线长度,用不等长缓和曲线代替原缓和曲线进行设计。 1)缓和曲线不得侵入有效站台。实际上,缓和曲线并非一定不能侵入有效站台,侵入时可增加选线的灵活性,对一些换乘枢纽的布局也更为合理,但此时需要对轨道、限界、区间等做特殊处理,对设计和施工存在一定影响[4]。 2)长度减少后的缓和曲线需满足超高顺坡率要求。超高顺坡率i不宜大于2‰,困难地段不大于2.5‰[5],一般按2‰控制。因i=h/LS≤2‰,则有h≤2‰LS,其中h为超高值。 3)长度减少后的缓和曲线需满足GB 50157—2013规定:曲线设置的最大超高应为120 mm,未被平衡超高不应大于61 mm,困难时不应大于75 m;车站站台有效长度范围内曲线超高不应大于15 mm。 4)限制超高时变率,保证乘客舒适度要求,满足LS≥0.007Vh,其中Vh为列车通过缓和曲线的最高速度,则有h≤LS/(0.007V)[6],其中V为列车通过速度。 优化后曲线半径增大,更偏向内侧,近站端缓和曲线变短。分析以下主要参数和性能的改善情况。 1)超高顺坡率 缓和曲线长度变短,首先超高顺坡率需满足GB 50157—2013要求。若缓和曲线长度不足,部分曲线超高在直线段完成,超高顺坡段可能侵入有效站台,但有效站台端部超高需不大于15 mm[7]。 2)超高设置 曲线地段的轨道超高[1]按下式计算。 (1) 目前国内地铁大多采用单一速度模式,最高设计速度为80 km/h或100 km/h,该运行模式下应满足超高h≤120 mm,欠超高hq≤61 mm,过超高hg≤61 mm[5]。缓和曲线长度变短时,应特别核算hq,hg是否在规范允许的范围内,并适当作出调整。 实际设置超高时,应首先结合行车牵引模拟计算,求得车辆通过曲线时速度的最大值Vmax、最小值Vmin及平均值Vp,然后计算对应速度下的超高最大值hmax、最小值hmin及平均值hp,hq=hmax-hp,hg=hp-hmin。根据规定: hq+hg≤61 mm+61 mm=121 mm (2) 在式(2)满足的情况下,需要分析超高顺坡率i,若i=h/L总≤2‰(L总为缓和曲线长度与直线上设置超高的长度的和),取超高h=hp;若i>2‰,说明超高设置不合理,应在h>hmax-61 mm的范围内降低超高值,并计算其他参数。 在式(2)不满足的情况下,即hq+hg>121 mm,一般要求限制通过整条曲线的最高速度Vmax,即Vmax≤V限,并在满足h≤61 mm+hmin的条件下,提高超高值h[8],其中: (3) 3)超高时变率 超高时变率按h≤LS/0.007V进行检算。 4)轮轨磨耗分析 根据相关研究,曲线段轮轨磨耗的影响因素有曲线半径、列车运行速度、超高设置、轨道刚度、车辆构造等[8]。 曲线半径是影响轮轨磨耗最关键的因素。曲线半径越小,轮轨磨耗越严重[9],钢轨更换周期越短。半径200 m曲线的换轨周期比半径400 m曲线的换轨周期缩短40%[10-12],当曲线半径小于400 m时,钢轨磨耗随着半径减小急剧增加。因此采用不等长缓和曲线设计时,提高曲线半径具有一定的实际意义和价值。 本文以青岛地铁6号线一期工程辛屯路站—朝阳山CBD站段为例,探讨不等长缓和曲线在站端小曲线半径优化中的应用[13]。 图3 辛屯路站—朝阳山CBD站线路平面图 该线最高设计速度为100 km/h,B型车6辆编组。图3为辛屯路站—朝阳山CBD站线路平面图。辛屯路站为起点站,沿滨海大道东西向布置,受制于下穿通道、军用电缆等,仅可在路北侧绿地内设站。出站后线路转至海岸大道,转角约96.7°,接朝阳山CBD站,该站已由先建13号线预留换乘节点,站位稳定。区间矿山法施工,无控制因素。2站站间距约1.04 km,内侧线路采用R=360 m、LS=65 m曲线设计,外侧线路采用R=380 m、LS=65 m 曲线设计。朝阳山CBD站侧的内、外侧曲线终点HZ点距离站台端部分别约为5.6,1.1 m,但未侵入有效站台;而辛屯路站侧的内、外侧曲线终点ZH点距离有效站台较远。本次主要研究朝阳山CBD站侧缓和曲线。 2站站位稳定,切线方向确定,转点JD坐标不变,以内侧曲线为分析对象,选取以下4种R、LS1,LS2组合。 原方案:R=360 m,LS1=65 m,LS2=65 m; 方案1:R=365 m,LS1=60 m,LS2=65 m; 方案2:R=370 m,LS1=50 m,LS2=65 m; 方案3:R=375 m,LS1=40 m,LS2=65 m; 方案4:R=380 m,LS1=30 m,LS2=65 m。 R>380 m之后,LS1太小,不再研究。表1是依据行车牵引曲线计算的相关参数。 表1 不同方案参数计算 3.2.1 参数变化分析 1)根据表1,最低速度随半径的增大而逐渐减少,半径每增大1 m,最低速度平均减小0.53 km/h,分析认为这是由于HY点随缓和曲线变短更靠近车站,HY点速度为列车通过曲线的最低速度,越靠近车站速度越低;最高速度随着半径的增大而增大,半径每增大1 m,最高速度平均增大0.11 km/h,基本位于曲线中部;平均速度逐渐降低,半径每增大1 m,平均速度减小0.18 km/h。 2)轨道超高值随半径的增大而降低,预设超高(一般取5 mm的整倍数,并且小于计算超高)也逐渐降低;当R≥370 m时,欠超高hq、超高顺坡率i超出规范一般要求,属于困难条件取值。 3)上述方案都满足舒适度指标h≤LS/(0.007V)。 4)上述方案都满足过超高指标hg≤61 mm。 3.2.2 方案分析 1)原方案和方案1:各项参数均满足规范一般要求,预设超高可作为实设超高,方案1曲线半径增大,最高通过速度提高,优于原方案。 2)方案2:由于i=2.2‰>2‰,hq=68 mm>61 mm,hq+hg>121 mm,可通过以下3种方法处理。 方法1:维持表1预设超高及顺坡率,i=2.2‰和hq=68 mm作为不突破规范的困难值使用。 方法2:维持表1预设超高,利用缓和曲线和直线同时顺坡,并通过限速,使i,hq不过超规范的一般要求,即i≤2‰,hq≤61 mm。 经计算,当i取2‰时,直线顺坡段长度l1=5 m,侵入朝阳山CBD站有效站台长度l2=3.12 m,有效站台端部超高h1=0.002l2=6.24 mm<15 mm。因hq=68 mm>61 mm,需通过式(3)限速,限速值V限=73.2 km/h。如此i、hq不超过规范的一般情况要求。 方法3:保持表1仅在缓和曲线段内顺坡,降低预设超高,并通过限速,使i、hq不超规范一般要求,即i≤2‰,hq≤61 mm。。 经计算,当i取2‰时,超高值h=100 mm,此时,V限=71.1 km/h。如此i、hq也不超过规范一般要求。 方法1中i、hq略偏大,根据铁路、地铁运营经验,i=2.2‰使列车脱轨的可能性极小,hq=68 mm不会降低旅客舒适度,外轨钢轨磨耗影响也并不明显;方法2超高顺坡段进入车站有效站台,对限界和结构存在一定影响;方法3限速幅度较大,失去增大半径的优势。综合分析,方法1较优。 3)方案3:i,hq突破和接近规范困难值,上述方法1不再适用。 采用方法2,当i取2‰时,直线段顺坡长度l1=12.5 mm,侵入有效站台长度l2=11.2 m,站台端部超高h1= 0.002l2=22.4 mm,不满足规范要求,需要按照站台端部不大于15 mm控制,反算求得顺坡率i=2.18‰。因hq=75 mm>61 mm,求得限速值V限=72.6 km/h。 采用方法3,当i取2‰时,h=80 mm,V限=66.9 km/h;i取2.5‰时,h=100 mm,V限=71.5 km/h。 方法2超高顺坡段侵入有效站台,站台端部15 mm 超高属规范限值,超高顺坡率按困难条件使用,并且需要限速,对施工和运营都存在一定影响;方法3限速较多,失去半径增大的优势。综合分析,2种方法相当。 4)方案4:i,hq均突破规范困难值较多,上述方法1、方法2不再适用。 采用方法3,i取2‰时,h=60 mm,V限=62.4 km/h;i取2.5‰时,h=75 mm,V限=66.2 km/h。 方法3限速较大,仅做比选。 3.2.3 方案推荐 利用不等长缓和曲线优化设计旨在增加曲线半径,设计时考虑施工因素及各专业常规化设计要求,且尽量在缓和曲线段内实现超高顺坡,避免顺坡段进入有效站台。当半径继续增大,缓和曲线进一步缩短,容易使欠超高超出规范而需限速,该速度应与原方案速度比较权衡,不能过分限速,使半径增大失去意义,这也反映了半径不能增大太多,使缓和曲线太短。 综上,推荐方案2,并按方法1计算,原半径为360 m 调整至半径为370 m,见表2。 表2 原方案与推荐方案参数对比 1)若站端曲线半径较大(400 m以上),采用上述方法曲线半径增加幅度较小,效果并不明显,反而使设计不常规,一般不适宜应用。 区间小半径曲线通常因控制因素限制,线路无法正穿而采取绕避措施,此时不能采用上述方法优化设计,而需要充分权衡风险源等级、限界要求、下穿地块难易程度、工程投资等,尽量采用不小于450 m的曲线半径。在特殊情况下,可拆除重建区间控制性建(构)筑物,取直线路,提高运营条件。例如,青岛地铁6号线一期工程,部分跨河桥采用桩基础,起初线路采用“外凸”形曲线从桩基两侧绕避。经与相关部门对接,桥梁年代较久,规模不大,投资可控,考虑地铁作为百年服务性民生工程,应提高标准,最终协议拆除还建桥梁,拟与地铁同期实施,区间线路调整为直线。 2)本文在优化中遵循“缓和曲线不侵入有效站台”的原则,这是考虑了超高设置与限界加宽处理较复杂,同时结构、建筑、屏蔽门等专业设施无法按照常规标准设计。但在特殊情况下,缓和曲线允许侵入有效站台。例如,宁波轨道交通2号线铁路南站与4号线呈斜T形换乘,由于条件限制,车站两侧均采用300~350 m曲线半径设计,缓和曲线侵入了有效站台,在设置曲线超高时,采取了圆曲线顺坡、缓和曲线分段顺坡的方式,在此基础上,参照GB 50517—2013《地铁设计规范》、STB/ZH-000001—2010《上海城市轨道交通工程技术标准》,计算出轨道加宽量。 3)尽量避免不等长缓和曲线与竖曲线重合。本文所述方法在增大曲线半径的同时,牺牲了缓和曲线长度,和常规曲线参数相比,增大了超高顺坡率。在竖缓重叠情况下,若竖曲线与超高点的凹凸形态不符,使轨道的铺设难度加大。但在困难条件下,采用1/2超高半抬半降方法,每条钢轨的超高顺坡率不大于1.5‰,两者可以重叠[5]。 4)采用不等长缓和曲线,相对增加了曲线轨道养护维修的工作量,对轨道工人素质要求较高[14]。 1)随着线路曲线半径增大,欠超高、超高顺坡率等参数有可能超出规范限值,最终需通过限速解决。根据轮轨磨耗理论,半径增大可降低轮轨磨耗程度,尤其半径在400 m以下时,轮轨磨耗对曲线半径更敏感。因此,若欠超高、超高顺坡率等参数能满足规范困难值要求,应以增大曲线半径为首要考虑因素,同时尽量避免“不常规设计”及过分限速,基于此,采用不等长缓和曲线优化设计站端小半径曲线时,推荐采用方案2,并按方法1进行计算。 2)站端曲线半径较大时,采用不等长缓和曲线设计意义不大,建议采用等长缓和曲线;区间线路因控制性建(构)筑物限制,同样不适宜采用上述方法,曲线半径尽量不小于450 m。 本文可为后续站端小半径曲线精细化设计提供一定借鉴,下一步将对相关问题进行探讨。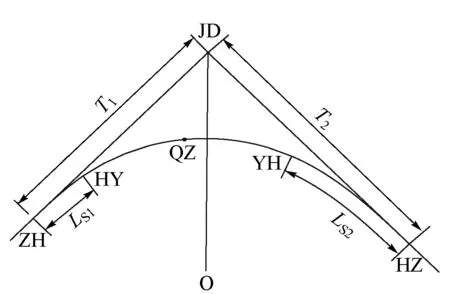
2 采用不等长缓和曲线优化设计
2.1 优化方法
2.2 优化原则
2.3 轨道参数分析方法
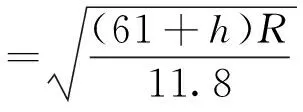
3 工程实例
3.1 工程概况
3.2 不等长缓和曲线优化设计
4 适用性分析
5 结论

