立体车库随机分配与就近分配库位布局探索

张海飞，李建国，王小农

(兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070)*

0 引言

随着社会的发展，城市人口日益增多，停车问题逐渐成为城市的一大难题.城市中有限的地面面积已无法提供足够的停车车位，于是向空间发展成为当前解决问题的一条重要途径，在一些规模比较小的小区或商业区，需要建设一些小型停车库，来解决停车难的问题.由于地理因素影响了车库的构造，所以在既满足地理因素又解决停车难问题的基础上，如何对车库的布局进行设计是一个亟需解决的问题.

以往的文献基本都是对车库的运行调度进行优化或改进，文献[1]研究了自动化立体仓库在多重搬运器与升降机下的动态存储.文献[2]应用排队论的思想，构造了立体车库设计方案的优化数学模型.文献[3]对巷道式立体车库的运行效率进行的分析.文献[4]根据排队论的理论基础，对立体车库中的选址、车流量、库存容量、作业效率等因素进行详细分析，对立体车库的流畅性进行了阐述.文献[5]以排队论为理论依据，提出了一种对立体车库进行规划设计的思路.

目前，针对车库的设计基本都停留在对其选址、运行效率、成本规划等方面，而缺少对车库整体如何构造、层列如何分配等问题的研究.本文根据前人思想，采用排队论的原理，给定堆垛机数量和I/O口位置，以顾客的平均等待时间和平均等待队长为设计参考，考虑车库内层列的不同组合对顾客平均等待时间和平均等待队长的影响，从而为车库的设计提供参考.

1 立体车库的实体模型

巷道式立体停车库，具有占地少、停放车辆多、先进的集中管理、安全可靠等优点，并且可根据环境和场地的要求定容，是解决城市静态交通问题的一种最为有效的方式.巷道堆垛式立体车库示意图如图1所示.

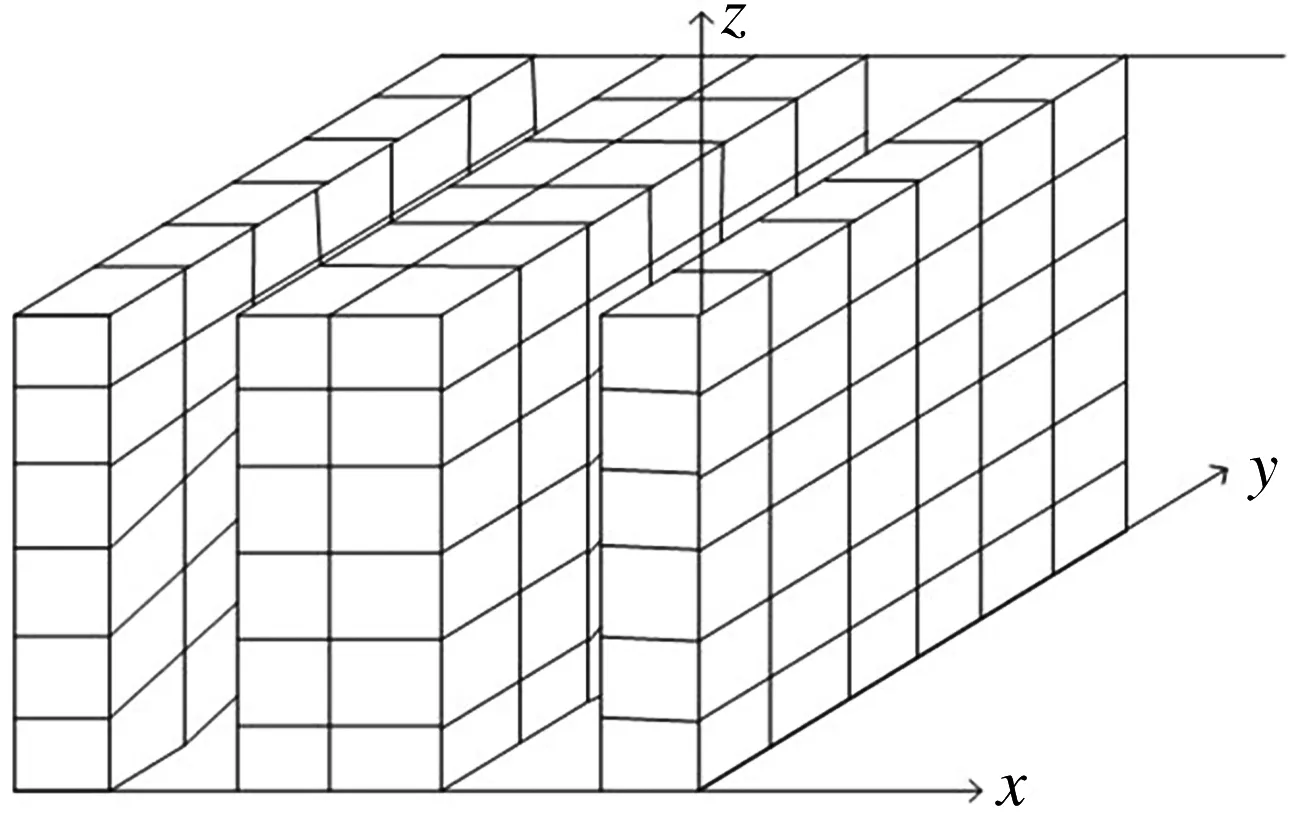
图1 巷道堆垛式车库示意图

由于存取车是三维运动，即水平X方向、垂直Y方向和高度Z方向的运动，每个车库的通道数也不相同，即存取动作中X方向运动不同，而每个巷道停车库位排列相同，相应库位存取动作中Y和Z方向运动就相同，所以又可取单巷道式立体车库作为车库的实体模型.如图2所示.

Z

库位……库位…………库位……库位库位……库位库位库位…库位

I/OY

图2单巷道立体车库单侧库位布局图

2 自动化立体车库的仿真模型

2.1 立体车库排队模型

把存取的车辆作为顾客，车库本身作为服务机构，则存取的汽车到来的时刻是随机的，服务的时间也是随机的.根据排队论的基本思想，立体车库存取车辆的过程可以看作为1个排队系统，如图3所示.

图3 车库车辆排队系统

本模型使用1台堆垛机，执行操作时每次只对1辆汽车进行存取，服务台数为1，可以认为整个车库运行符合M/M/1排队模型.顾客服务规则为先到先服务(First Come First Service， FCFS)，堆垛机在对车辆进行存取之后返回I/O口.由排队论基本理论可知，对1个停车库而言，车辆到达及存放时间都是随机离散的，车流符合泊松分布，在仿真时取按泊松分布到达的时间间隔序列为车辆的存放时间.

系统内有1个服务窗口，服务窗口的服务时间服从负指数分布，服务强度为μ，系统容量为m.如果车厅内车辆已满，新来的车辆将直接离去，则系统内必定有m-1个可供车辆排队的位置，即车厅容量为m-1.为满足车辆对服务窗口的使用需求，选取车辆到达率为λ，则系统的服务强度为ρ=λ/μ.

2.2 立体车库运行指标

《车库建筑设计规范(2015)》规定，1个I/O口对应约50个停车位，I/O口处应设置不少于2个的候车位，当I/O口分开设置时，候车位不应少于1个.但是规范中明显缺少了对车位如何进行布局的规定.考虑立体车库的造价等问题，立体车库的最低层数为3层.堆垛机水平速度v1=80 m/min，垂直速度v2=20 m/min.车库车位的长L0=5 m，宽W0=2 m，高H0=1.8 m.

因为顾客到达规律服从参数为λ的泊分布，服务时间服从参数为μ的负指数分布，则λ表示单位时间内平均达到的顾客数，μ表示单位时间内能服务完的顾客数.

车辆在从I/O口运送到存放位置所需时间T为：

(1)

其中,i为停车位所在的层，j为停车位所在的列，i、j为正整数.

车库共有N个停车位，车辆到达率为λ，则系统的服务强度为ρ=λ/μ，则停车排队系统空闲概率P0为：

(2)

其中，k表示有k辆车停放.

车辆在系统内平均等待时间为：

平均等待队长Lq为：

根据自动化立体车库的数学模型，堆垛机数量为1台，出入口数量为1个，车辆到达时间服从参数为λ=0.3(辆/min)的泊松分布，车库服务率μ=0.9(辆/min)，考虑1天即1 440 min内车库运行情况，车辆按照随机存储方式和就近存储方式进行存储.

则系统运行时顾客的平均等待时间为：

(5)

综上，对整体模型进行模拟建模，以顾客的平均等待时间和平均等待队长为衡量标准，分析随机库位分配和就近库位分配两种方式.对车库车位布局进行探索，合理规划车库层列布局.

3 系统仿真

本文考虑设计停车位N为50个，车库整体构造为双排对列布设，则每排车库的停车位n为25.再考虑整个立体的车库的造价等问题，立体车库的最低层数为3层，则可得出表1的立体车库层和列的不同组合.

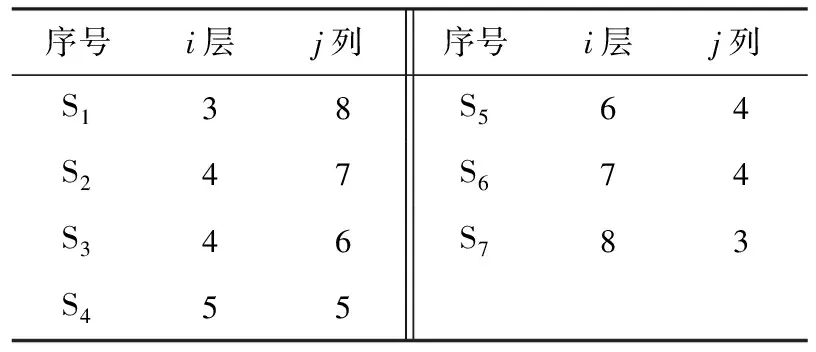
表1 层和列不同情况的组合

针对上述7种层和列不同情况的组合，假设堆垛作业方式为单一作业，顾客的平均等待时间对比如表2所示.

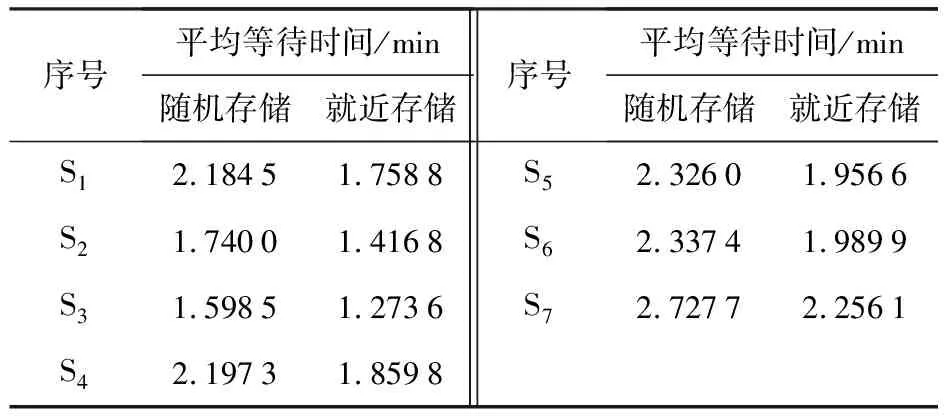
表2 不同情况下顾客平均等待时间

(a) 随机库位分配 S3情况下顾客等待时间

(b) 就近库位分配 S3情况下顾客等待时间

针对上述7种情况所对应的顾客平均等待时间，分析最优布局下两种分配方式的顾客平均等待时间仿真对比图如图4所示.

不同情况下顾客平均等待队长如表3所示.

表3 不同情况下顾客平均等待队长

通过上述仿真建模的结果，可以看出：

(1)S3情况下，即4层6列双排对列布设，顾客的平均等待时间最短；

(2)随着层数变大，列数变小，顾客的平均等待时间逐渐变大，平均等待队长变长.

(3)就近库位分配方式比随机库位分配方式，每种布局下顾客平均等待时间缩短大约0.33min，平均等待队长缩短了约0.07.

此仿真在考虑设计停车位N为50个、双排队列布设时进行，若考虑设计停车位N为100个、双排队列布设，则需考虑不同的假设条件：若为单巷道则车库的库位布局有不同的布局；若为多巷道则需考虑堆垛机在X方向上运行的时间.

4 仿真结果分析

对顾客的平均等待时间进行分析可知，当车库层数大于等于4层时，随着层数的增加和列数的减少，顾客的平均等待时间逐渐增加，但在相同库位S2和S6两种不同库位布局下，S2情况下顾客平均等待时间小于S6情况下顾客平均等待时间.

发生该现象的主要原因在于，堆垛机将车辆从服务台运送到库位所需时间是由max(0.09i,0.025j)+0.0625决定的，从该式可以看出堆垛机将车辆从服务台运送到库位所需时间取得是一个最大值，在对车辆进行存储时，4层7列(S2)情况下i的取值范围为1≤i≤4，j的取值范围为1≤j≤7，而7层4列(S6)情况下i的取值范围为1≤i≤7，j的取值范围为1≤j≤4；在计算时间时层数i的系数为0.09，列数j的系数为0.025，则在相同库位下，堆垛机对库位的访问S2情况比S6情况所需访问的层数要小得多.S1和S7两种情况也是相同原因.同理可分析顾平均等待队长.

分析表2和表3中的数据可知，顾客的平均等待时间与顾客平均等待队长有着必然联系.堆垛机在对车辆进行存取时，堆垛机在库内运行时间越长，顾客排队等候的时间也就越长，顾客平均等待队长也就越长.而堆垛机在库内运行时间则与库位布局息息相关，因此，库位布局越合理，顾客的平均等待时间与顾客平均等待队长也就越短.

5 结论

本文在单巷道自动化立体车库下进行模拟仿真，针对巷道堆垛式自动化立体车库库位布局对顾客平均等待时间和平均等待队长的影响，模拟了不同库位布局下顾客平均等待时间和平均等待队长，主要表现在：

(1)通过省略车库垂直升降的部分，把立体车库的三维立体图简化为二维平面，建立了巷道堆垛式立体车库的简化模型；

(2)综合分析了《车库建筑设计规范(2015)》中的相关规定，使得模拟具有可靠的依据，所涉及数据具有一定的真实性；

(3)在M/M/1排队系统下，分析了7种不同库位布局，采用大量数据进行仿真，使得结果具有一定的可靠性.

从仿真结果来看，在M/M/1排队系统单服务台，队长无限，FCFS下，考虑库位双排对列布设，每一排在4层6列的库位布局下，顾客的平均等待时间相对其他布局下的顾客的平均等待时间较短，而该种库位布局也满足《车库建筑设计规范(2015)》.

但在建模时仍存在不足，例如：堆垛机在对车辆进行存取时仅仅考虑了将车辆进行存取后回到I/O口，不同时段顾客的到达率也相同等，针对以上问题仍需要进行进一步的探讨.