无鉴相角度域滚动轴承故障诊断方法研究

刘芝博，苑宇，田丽，芦鹭

(1.大连交通大学 机械工程学院，辽宁 大连 116028；2.大连交通大学 机车车辆工程学院，辽宁 大连 116028)*

0 引言

滚动轴承是机械设备中最常见的零部件，其工作状态直接影响了机械的精度、准度及寿命.变转速工况在实际工业生产中更为常见，且因变转速工况下振动信号在时域是非平稳信号，所以传统的信号分析方法不容易识别和诊断出故障[1].针对上述情况，本文提出了基于经验模态分解(EMD)的当量转速的阶比分析.阶比分析能够有效解决转速波动问题，其最关键的是利用转速信号对振动信号进行角度域重采样.因此本文利用EMD来分解振动信号，并求出每个单分量信号的瞬时频率.再利用瞬时频率估计单分量信号的转速，结合各自的转速对单分量信号进行角度域重采样，将时域内非平稳信号转化为角度域内平稳信号.在角度域内对信号进行重构，并对重构后的信号进行阶比分析.

EMD是常用的信号分析方法，它在对IF深入分析的基础上提出了内蕴模态函数(IMF)的概念，认为信号都可以自适应的分解为若干内蕴模态函数之和[2-3].且为了提高结果的精度，本文提出了利用高斯拟合对原数据进行延拓的方法来改善EMD的端点效应.

1 基于EMD的瞬时频率估计

1.1 经验模态分解

从物理学角度，信号可分为单分量信号和多分量信号两大类.单分量信号在任意时刻都只有一个频率，该频率称为信号的瞬时频率.多分量信号则在某些时刻具有各自的瞬时频率.所以为了得到有意义的瞬时频率，定义了内蕴模态函数：

(1)在整个信号波形中，极值点的个数和过零点的数目相等或最多相差一个；

(2)在任意时刻，由局部极大值点和局部极小值点形成的上、下包络线的平均值为零，即信号关于时间轴局部对称.

(1)

任何复杂的信号都可以写成形如式(1)中不同的内蕴模态函数和残差之和[4].

1.2 瞬时频率的估计

不同于传统傅立叶分析中一般指周期性信号的频率概念，瞬时频率是变化着的频率[5-6]，更适用于实际生产生活中在变转速情况下的机械，步骤如下：

(1)设x(t)为时域内一个连续信号：

x(t)=a(t)cosφ(t)

(2)

(2)通过Hilbert变换求得x(t)的共轭信号：

(3)

(3)由信号x(t)和q(t)可构成一个复共轭对，原信号为其实部，共轭信号为其虚部，得到解析信号：

z(t)=x(t)+jq(t)=a(t)ejφ(t)

(4)

(4)则信号x(t)的瞬时频率为：

(5)

1.3 EMD的端点效应

EMD作为一种自适应的分解方法，被广泛应用，但同时也存在着端点效应的问题[7].本文将振动信号进行分解后再合成，所以分解误差会对结果造成很大影响.因此本文提出了利用高斯拟合的方法，分析出原始数据的走向，并将两端点分别向外延拓并与原数据结合，这样可以有效判断原数据的端点是否为极值点，一定程度上抑制了端点效应问题.

(6)

高斯拟合(Gaussian Fitting)即形如式(6)的高斯函数对数据点集进行函数逼近的拟合方法.其实可以跟多项式拟合类比起来，不同的是多项式拟合是用幂函数系，而高斯拟合是用高斯函数系.使用高斯函数进行拟合，计算积分十分简单快捷，这一点在很多领域都有应用.在拟合方法上以最小绝对残差为标准，让拟合的曲线最大程度上贴合原数据，使数据更可靠.

图1是以chip信号为例，从采样率为500的信号中截取一部分，左端点为原信号的极小值点，右端点为原信号的极大值点，1(a)为对原信号直接EMD分解时极大值极小值形成的上、下的包络图，1(b)为将信号高斯拟合延拓后再进行EMD分解得到的包络图，从图中可以看出，利用高斯曲线拟合延长后的数据，可以有效的判断原数据的端点是否为极值点，更完整的保留了原数据所包含的信息.

(a)改进前信号的包络图

(b)延拓后的包络图

2 基于瞬时频率的无鉴相角度域阶比分析

近年来，无转速计阶比分析技术发展迅速，因为无需光电编码器等鉴相装置(这种方法称为无鉴相技术)，不仅节省硬件成本，还简化硬件需求，便于实际测量.实现无转速计阶比分析的关键，在于利用一系列信号分析处理的方法从振动信号中估计转速信号[8].郭瑜和秦树人等人提出利用峰值索引的方法从振动信号时频分布图中得到瞬时频率，从而估算转速；赵晓平利用短时傅立叶变换求得瞬时频率进而估计转速.但是这些方法只有在特定情况下才能用于多分量信号.本文提出一种基于EMD求取瞬时频率，实现无转速计阶比分析的方法，流程如图2所示.

图2 基于EMD的无转速计阶比分析流程图

具体步骤如下：

(1)由加速度传感器获取滚动轴承振动信号；

(2)用改进后的EMD将时域的多分量振动信号分解为单分量信号；

(3)用Hilbert变换法求取各单分量信号的瞬时频率，根据各自的瞬时频率确定每个单分量信号的转速；

(4)根据每个单分量信号的转速计算等角度采样的鉴相时刻；

(5)根据等角度采样的鉴相时刻对单分量信号进行重采样，将时域非平稳信号转换为角度域的周期平稳信号；

(6)将每个单分量信号对应的角度域信号进行重构得到原振动信号的角度域信号.

(7)对角度域波形进行快速傅里叶变换，获得原振动信号的阶比谱.

2.1 转速及鉴相时标估计

阶比分析的关键是利用转速信号对振动信号进行角度域重采样，无转速计阶比分析的实质是要获得旋转机械参考轴的瞬时转速ni(t)，其中i代表瞬时[9].显然参考轴的瞬时转速与瞬时频率fi(t)满足下列对应关系：

ni(t)=60×fi(t)

(7)

振动信号经EMD分解得到单分量信号后，通过Hilbert变换求得每个单分量信号的瞬时频率.瞬时频率经过式(7)计算得到了每一刻的瞬时转速，通过瞬时转速在和采样的时间间隔dt相乘再乘上360°即可获得每一个时刻所转过的角度，通过转过的角度进行累加后，进行等角度划分.通过划分好的等角度信号，再对时间进行插值，得到等角度采样的鉴相时标.

4.目标的统一性。创编校本课程也好，把流行音乐引入课堂也好，都是为了提高课堂的有效性、准确达到教学目标，能够更好地培养学生的审美能力和鉴赏能力，为学生终身学习打下坚实的基础。

2.2 单分量信号角度域重采样

与等时间采样相对应，不按照等时间间隔采样，而采用等角度间隔采样的方法，称为等角度采样，又叫同步采样[10].同步采样是阶比分析的关键.之所以采用同步采样，而不用等时间采样，是因为在转速变换或者转速波动的时候，信号不再保持原有的周期特性，使得原本离散的频率谱线变为连续的频率带，会造成频谱模糊的现象，使得频谱分析失效.等角度重采样原理如图3所示.

图3 等角度重采样原理图

在求得角度域转速后，根据角度，过对原始数据进行插值实现等角度重采样，可以求出振动信号角度域里对应采样时间的幅值，在仿真和实验中，Lagrange线性插值已经取得很好的效果.插值公式如下：

(8)

令每周采样点数为m，转速为N，则有角度重采样频率Fs：

(9)

2.3 信号重构

将得到的每个单分量的角度域信号进行重构，合成原理图如图4所示，前3个分别代表了3个IMF分量对应的角度域信号.

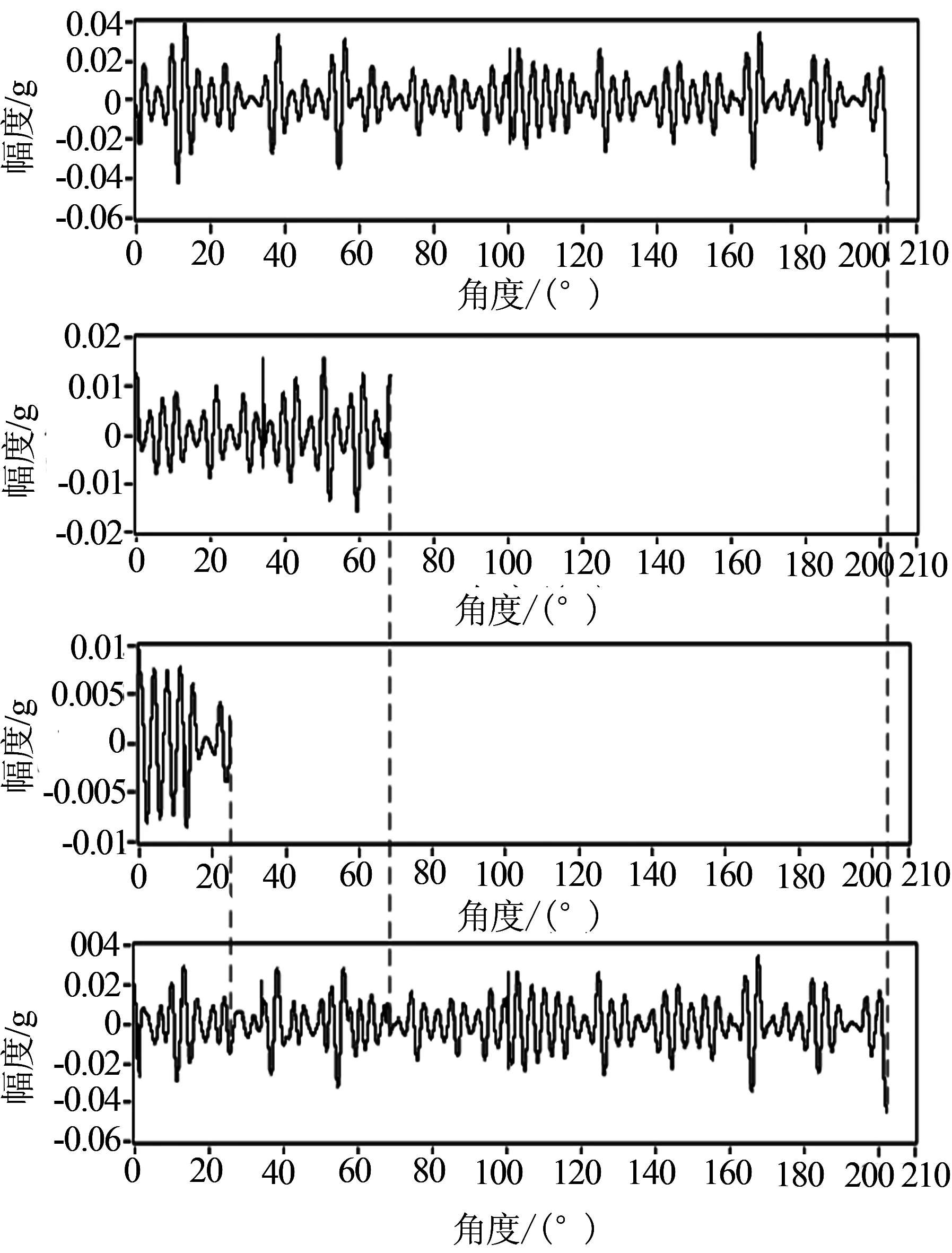
图4 合成原理图

EMD是将复杂信号自适应的分解为若干IMF之和，但对于某些复杂信号，EMD分解获得的时频分布与原信号的时频分布并不一致，有时会出现已经被认为是单分量信号的一个IMF还能继续分解，或者由几个单分量构成的信号分解后得到完全不同的几个单分量信号[11].所以为了获得原始信号完整的信息，将求得的每个IMF的角度域信号进行重构.

2.4 阶比谱的获得

在得到完整的角度域转速信号后，对其进行傅里叶分析，就可以得到振动信号的阶比谱，从该谱中可以很好的观测信号的特征阶次.

表1 各阶比跟踪算法比较

3 滚动轴承故障诊断实例

采用QPZZ-Ⅱ系统实验台，测得滚动轴承的振动信号.该系统可以快速模拟旋转机械多种状态及振动，可进行各种状态的对比分析及诊断.轴承型号为N205，实用NI-USB6210数据采集卡采集振动信号.轴承相关参数如表2所示.

表2 滚动轴承参数表

根据滚动轴承外环故障、内环故障特征频率计算公式如下所示：

(10)

(11)

结合表2和上述公式计算得到内环故障阶次为7.75；外环故障阶次为5.22.

图5(a)为外环故障的振动信号，其采样频率为25 000 Hz，在有加载的情况下由1 500 r/min做减速，数据长度为303 616，以EMD产生的前三个IMF为例：

图5(b)为前三个IMF分别通过Hilbert变换方法得到的瞬时频率，图5(c)为利用各自瞬时频率求出相应转速后，再分别对各自的IMF进行角度域重采样后得到的角度域图，将所有得到的角度域图进行重构，就得到图5(d)，再对图5(d)进行傅里叶变换得到阶比谱图5(e)，可以看出在阶比为5左右时，有非常明显的波峰.

(a) 外环故障振动信号

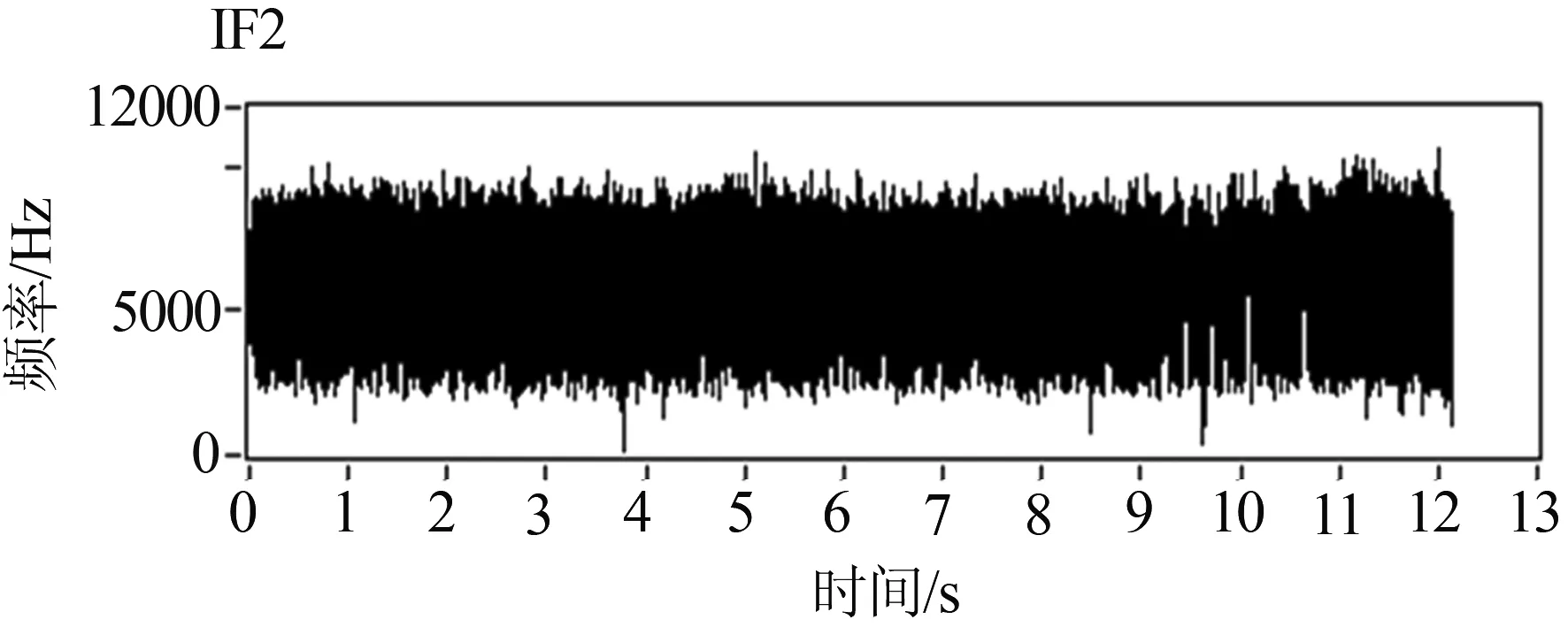
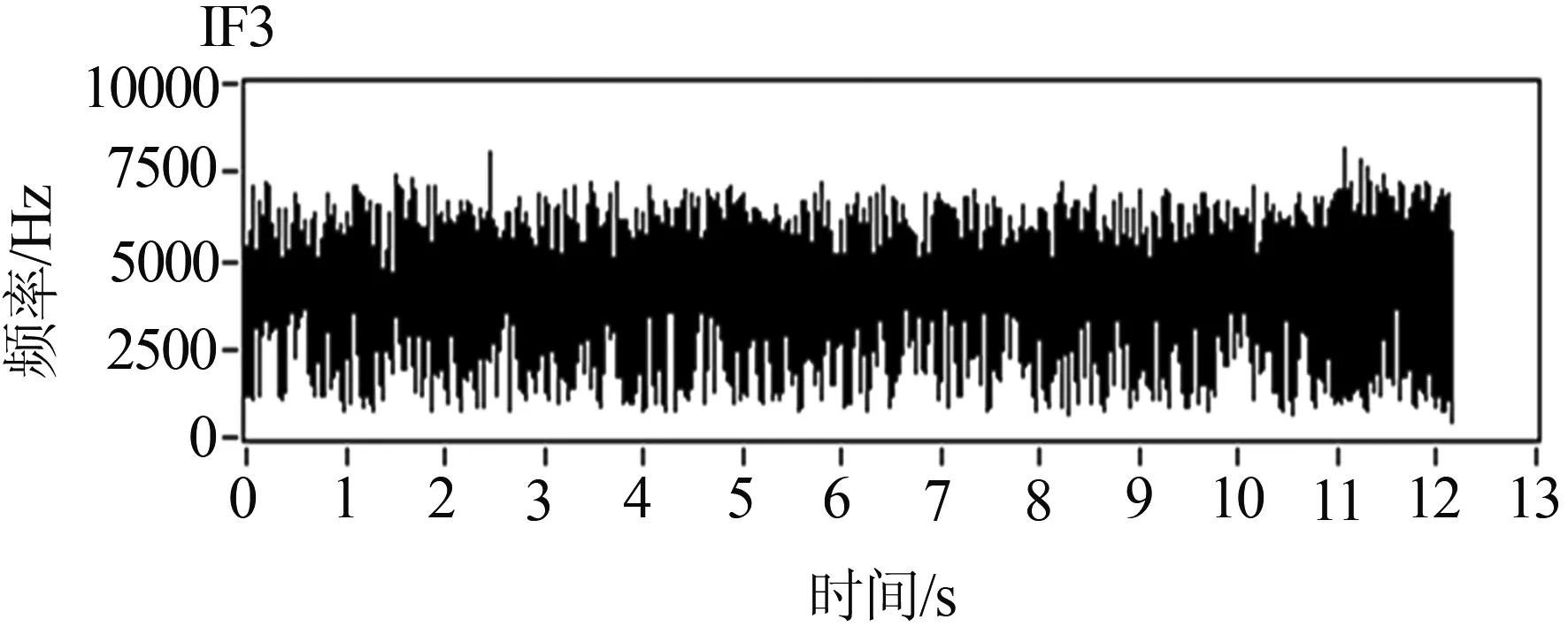
(b) 瞬时频率图

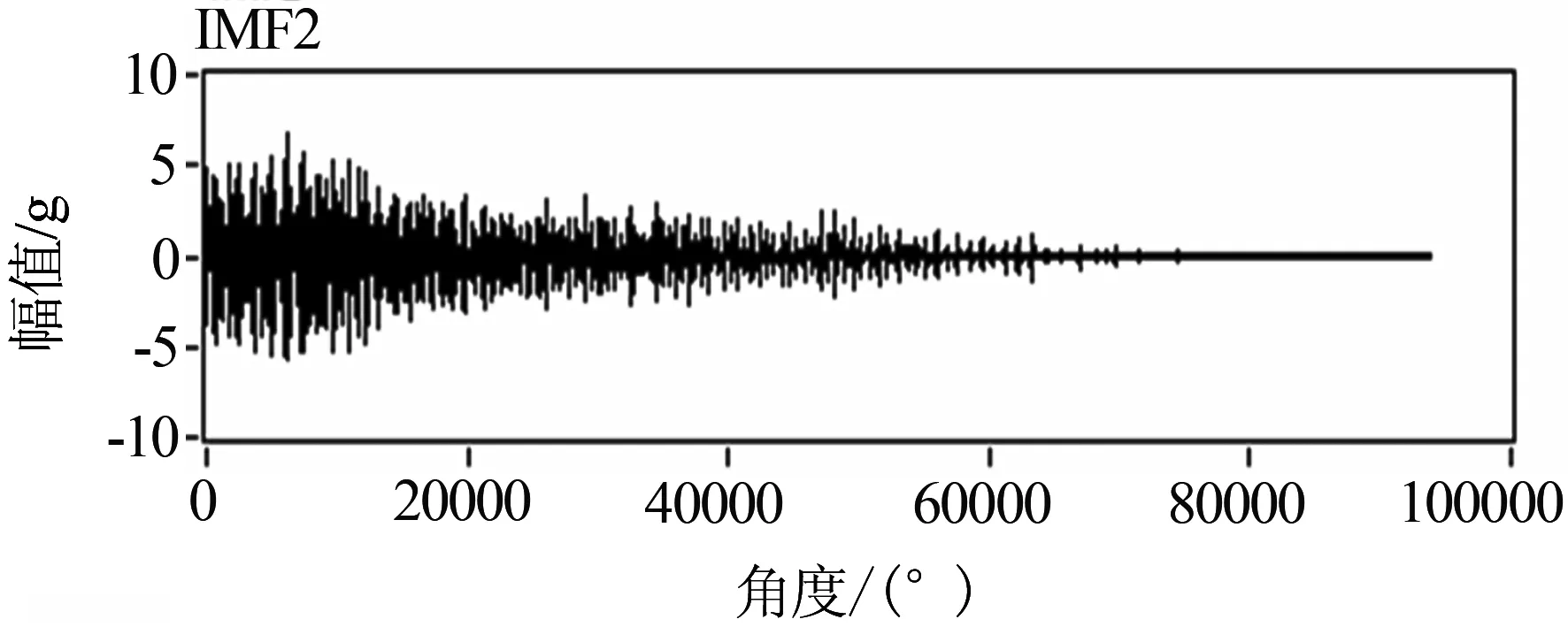
(c) 等角度域重采样图

(d) 角度域信号重构图

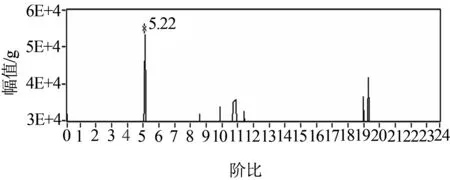
(e)阶比谱

(a)内环故障振动信号

(b)阶比谱

图6(a)为内环故障的振动信号，采样频率25 000 Hz，在无加载的情况下从1 500 r/min做减速，数据长度为317 952，分析过程同上，从阶比谱图6(b)中可以看出在阶比为7～8之间时，有非常明显的波峰.

4 结论

本文提出了一种无需使用鉴相器的情况下诊断变转速旋转机械滚动轴承故障的方法.

首先EMD对轴承振动信号进行分解得到单分量信号IMFs，在进行EMD的过程中，利用高斯拟合来判断信号的走向，对信号进行延拓，这样就可以有效的判断出原数据的端点是否为极值点，更完整的保留了原始数据的有效信息在一定程度上抑制了端点效应.

再利用Hilbert法求出每一个IMF对应的瞬时频率，由瞬时频率和瞬时速度的关系来估计每一个单分量信号的转速，并利用各自的转速对相应的单分量信号进行角度域重采样，把时间域内的非平稳信号转化为角度域内的平稳信号.再将这些角度域信号进行重构，通过傅里叶变换得到滚动轴承震动信号的阶比谱，通过观察阶比谱并与数据计算相对比，可以判断出滚动轴承的故障类型.

最后将该方法与传统的计算阶比跟踪算法进行比较，结果表明该方法可以有效提取故障信号的特征频率，不仅无需额外安装鉴相器节省硬件，且对转速没有限制，能够进行在线分析，更有利于阶比分析在故障诊断中的应用.