平直翅片管式换热器结构参数的优化
费继友, 田士博, 王枫, 李花
(大连交通大学 机车车辆工程学院,辽宁 大连 116028)*
0 引言
平直翅片式换热器作为一种能源工业的重要设备,以其结构简单、工艺成熟、互换性高等特点得到广泛应用.尽管此翅片结构可以降低空气流阻,增加传热面积进而强化换热效果,但往往存在着扰流强度弱,换热效率低,整机体积大的缺点[1].因此对平直翅片式换热器进行结构优化研究,有助于提高换热效率及增强结构紧凑性.
目前,平直式换热器的优化多以单目标函数进行研究[2-5],例如:换热因子j、阻力因子f、换热量等,且对换热器体积的研究较少.康海军[2]、阴继翔等[3]以阻力因子f,PEC(综合性能评价指标)分别为单目标函数对平直翅片结构进行优化,仅提高了换热器效率.马士伟[4]、叶立平等[5]以换热量为单目标函数对平直式翅片结构进行分析,仅提高了其换热量.然而对于换热器而言,评价其换热效率的标准绝非单一目标即可,由于这些目标互相耦合,互相关联,所以需要多目标同时参与并行分析,往往要进一步对翅片结构进行多目标优化设计.而遗传算法可以较完美的解决多目标优化问题,杨辉著等[6]利用遗传算法完成了板式换热器的多目标结构优化,徐东等[7]利用遗传算法完成锯齿型翅片的多目标结构优化.另外,由于换热器在制冷设备中所占体积较大,其体积的优化对整机的紧凑性有着重要影响,在平直式翅片换热器的优化设计中,还缺乏多目标优化下对体积的研究.
因此,本文以平直翅片管换热器为研究对象,在维持入口雷诺数恒定时,基于遗传算法以最大换热因子j,最小流动阻力f,最小换热器体积Vhe为目标函数对翅片间距,管径,横向中心距,纵向中心距进行优化设计.
1 换热器数值模拟方法及计算模型
本文计算模型中的对流换热过程遵循质量守恒、动量守恒、能量守恒,并采用有限体积法对其进行离散,模拟计算采用SIMPLE算法,动量及能量方程使用二阶迎风格式[8].
1.1 控制方程及湍流模型
本文所用方程包含质量、动量、能量控制方程如下:
质量方程为
(1)
动量方程为
(2)
能量方程为
(3)
流体在翅片间圆柱绕流的情况十分复杂,为模拟这一情况,工程上常采用半经验的标准k-ε方程[8]如下:
(4)
(5)
1.2 目标因子定义
(1)阻力因子
(6)
式中,ΔP为进出口空气压降,Pa,ρ为流道中空气的密度,kg/m3,μmax为流道最小截面处空气流速,m/s,De为圆管当量直径,m,L为翅片沿空气流通方向的长度,m.
(2)换热因子
(7)
式中,Nu努塞尔系数,Re为雷诺系数,Pr为普朗特系数;
(3)换热器体积Vhe,本模型中所计算的体积为图1中翅片,管壁以及计算域体积,不包含进出口的延长部分,单位为m3;
1.3 翅片管几何模型
换热器翅片结构数量庞大,为减少CFD模拟计算成本,需将模型做必要的简化处理.如图1,

(a)
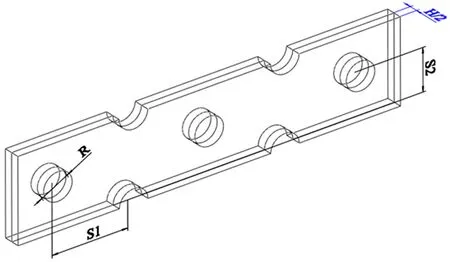
(b)
针对目前平直式翅片换热器常用结构参数范围,以H取1.4~2.6 mm,R取5~9 mm,S1取16~21 mm,S2取8~13 mm为优化范围.
1.4 网格划分及边界条件
利用ICEM模块生成精度更高的参数结构化网格可以很好的与Fluent进行实时关联,同时为保证捕捉避免流动特性,对近壁面网格进行局部加密处理,如图2所示.

图2 网格边界层加密示意图
为保证模型计算精度,对模型进行网格无关性验证,图3为j和f随网格数量从17 320加密至661680变化的曲线,可以观察到网格数量在320000时,变化趋于平缓,考虑计算的精度以及计算的成本和周期,选择网格数量为320 000进行计算.

图3 网格无关性验证
模拟计算时,边界条件设置如下:
(1)入口:流体域空气进口为速度入口,空气流速均匀分布;
(2)出口:流动状态未知,故为自由出流;
(3)翅片:翅片与流体接触表面采用自身导热和表面对流换热的耦合方式;
(4)热管:忽略圆管的厚度,认为管内外壁面的温度相同,设定热管的壁面为恒温壁面,温度为316 K,其余几何体模型表面均设置为对称性边界条件;
(5)翅片材质为铝,管壁材质为铜,且忽略外界辐射换热及由于铜管与翅片接触不良产生的热损失,通道流体为空气,视为常物性.
1.5 数值模拟的正确性验证
仿真算法验证所用结构参数如下:H为2.00mm;F为0.15 mm;R为7.00mm;S1为18.20 mm;S210.50 mm.
为保证仿真计算结果准确性,以上述结构参数,改变入口风速(2.5~6.5 m/s),得到衡量空气阻力的系数f,以及衡量换热的系数j.将仿真计算结果与文献[10]中实验值进行对比,如图4可知,f因子与实验对比,均方根误差为8.07%,j因子与实验对比,均方根误差为1.66%,吻合度较好,虽然在低雷诺数最大误差达到20%,但实际工况雷诺数要远大于此,因此可以认为数值算法切实可靠.
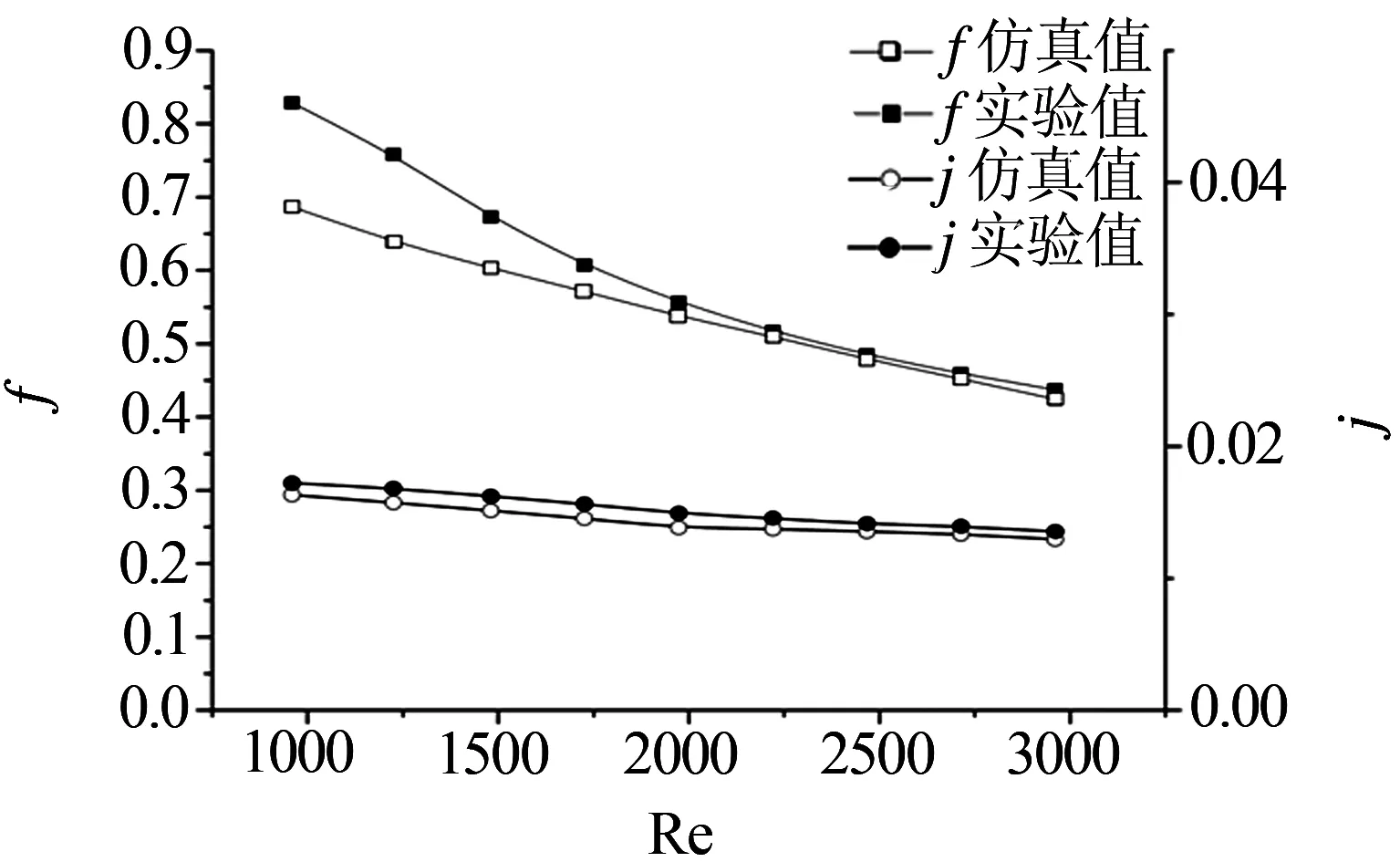
图4 仿真模拟与实验数值结果对比
2 换热器数值模拟结果分析
2.1 翅片间距H的影响
如图5,R=7 mm,S1=18.5 mm,S2=10.5mm时,不同翅片间距H(1.4~2.6 mm)对f因子、j因子、体积Vhe的影响.如图5可知,随着翅片间距H的增加,阻力系数f下降,换热因子j上升,体积Vhe增加.随着H的增加,导致空气流道的扩大,流速下降必然使流动阻力下降,进而促进湍流充分发展,带走更多热量最终导致换热因子f的增加,但由于间距的增加,为保持相同的换热面积,必然使整机体积增加.增加H有利于强化换热,但考虑到整机体积,应在允许的空间条件下适当增加翅片间距.

图5 翅片间距 H对换热及体积的影响
2.2 管径R的影响
如图6,H=2.0 mm,S1=18.5 mm,S2=10.5 mm时,不同管径R(5~9 mm)对f因子、j因子、体积Vhe的影响.如图6可知,随着R增加,阻力系数f增大,换热因子j减小,体积Vhe是不变的.随着管径R增加,流道中管路阻挡面积扩大,进而使流动受阻加剧,压降升高,使阻力系数f快速增加,由于流动受阻严重,湍流得不到有效的扩展,热量不能及时的随主流流出,最终导致换热因子的下降.由于管径的改变不影响相邻管路的中心距离,翅片所在的整体空间不发生尺寸变化,所以体积是不变的.不论从换热效率还是工程成本考虑,小管径已成为必要的发展趋势,但考虑管内制冷剂的流动阻力,应结合使用工况下选取适当的管径.
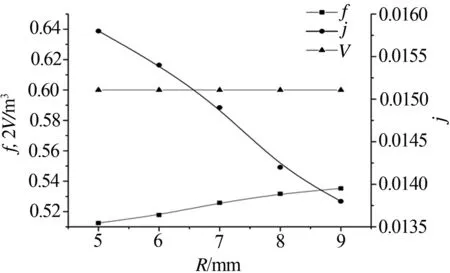
图6 管径 R对换热及体积的影响
2.3 管横向间距S1的影响
如图7,H=2.0 mm,R=7.0 mm,S2=10.5mm时,不同横向中心距S1(16~21 mm)对f因子、j因子、体积Vhe的影响.随着S1的增加,换热因子j下降,阻力系数不断上升后趋于平缓,体积Vhe线性增加.随着S1增加,管路之间横向距离的增加,降低了最小截面流速,使湍流扰动程度下降,且流体流动长度增加使其流动阻力增加,长度的增加导致热量不能及时的导出,进而使换热因子j呈下降趋势,横向间距的增加必然导致翅片宽度的增加,导致其体积线性增长.横向间距对f,j,Vhe均有显著的影响,不论从换热效率还是从体积上分析,可见S1应越小越好.

图7 横向间距 S1对换热及体积的影响
2.4 管纵向间距S2的影响
如图8,H=2.0 mm,R=7.0 mm,S1=18.5mm时,不同纵向中心距S2(8~13 mm)对f因子、j因子、体积Vhe的影响.随着纵向间距S2的增加,换热因子j,阻力系数f均下降,体积Vhe线性增加.随着S2的增加,迎风流道面积增加,空气流通速度下降,进而流动阻力下降,由于翅片间距不变,而S2的增加相当于翅片高度,进而导致湍流进一步发展恶化,并不能起到促进换热的作用,所以换热因子j呈下降趋势,同时S2的增加,必然导致计算域体积扩大,所以导致体积Vhe的增加.阻力因子f下降幅度相对较大,可以认为S2增加对换热效率有利,但要考虑其带来的体积增长,所以应该适当选取合适的S2.

图8 纵向间距 S2对换热及体积的影响
3 多目标优化结果分析
3.1 多目标优化原理
本文所用多目标遗传算法(MOGA)的优化过程如图9.对于换热器结构的优化,不仅要求具有充分的换热效果,较低的空气流动阻力及更小的体积结构.为兼顾三者,首先在试验设计中使用精度高,预测性好的中心组合设计,是响应曲面中最常用的二阶实验设计[11].然后根据试验点建立响应面方法构建目标函数,响应面方法是一种通过已知点来预测未知或需要观察点的插值方法,其利用方差的变化来表达空间的变化,可以保证由空间分布得到的预测值的误差最小,使结果良好的全局性及预测性.最后利用遗传算法对目标函数进行迭代求解并利用Pareto机制对解集进行最优选取[12].

图9 遗传算法优化流程
在多目标优化中,各个目标函数往往是互相矛盾的,不存在一组解使所有目标函数达到最优值,经多目标遗传算法求近似解的分析方法,克服了以往单目标分析的不足,在对换热器结构优化的处理上非常有效[13].
3.2 多目标优化处理
基于Workbench的目标驱动优化系统,对模型进行参数化建模,并使全局网格参数化,设定换热因子j,阻力系数f,换热器体积Vhe为目标函数,维持雷诺数为2219时,根据各结构常见的变化范围,给予结构参数优化尺寸如表1.在优化模块中,选取精度高的中心组合设计并生成正交试验表格.优化算法选用多目标遗传算法,设置响应面生成样本点1000,迭代样本200,允许max pareto为70%.换热因子j最大化,阻力因子f最小化,翅片体积Vhe最小化.

表1 结构参数变化范围 mm
3.3 多目标优化结果分析
表2为以最大换热因子j,最小阻力系数f,和最小体积Vhe为目标函数对翅片间距、管径、热管横向中心距、热管纵向中心距的优化结果.维持雷诺数为2 219时,有必要考虑实际生产当H=2.6mm,R=7.00 mm,S1=17.20 mm,S2=8.50mm时,阻力系数f减少26.30%,换热因子j提高1.11%,体积Vhe减少13.93%.优化结果为减小体积而牺牲了基管的衡纵间距,进而使换热面积减小,最终导致换热因子下降.为弥补j因子的下降,采用维持小管径而略增大翅片间距的措施来保证原有的换热效率,较大的间距不仅补足了原有换热因子的下降,而且降低了阻力因子f,进而降低设备运行成本.综合认为换热器在维持原有的换热效率时,体积及空气流动阻力均有下降,由此可见,利用多目标遗传算法,可以有效的对平直式翅片换热器进行优化设计.
4 结论
利用Workbench目标驱动优化系统,以最小f因子,最大j因子,最小Vhe为目标函数,应用多目标遗传算法对平直翅片式换热器的翅片结构参数进行优化计算,得出以下结论:
(1)维持入口雷诺数为2 219时,翅片间距H=2.60 mm、管径R=7.00 mm、 管横向间距S1=17.20 mm,管纵向间距S2=8.50 mm时性能较佳,其阻力系数下降26.30%,换热因子提高1.11%,换热器体积减少13.93%;
(2)基于Workbench多目标构优化技术,可以有效的克服传统优化方法不全面的缺点,以及对实验关联式的依赖,有助于提高实验效率,保证结果精度,具有实际的参考意义.
表2结构优化结果

H/mmR/mmS1/mmS2/mmfjVhe/m3优化前2.007.0018.5010.500.890.01380.28优化后2.587.4217.238.690.670.01440.22工程化分析2.607.0017.208.500.650.01390.24变化率-26.30%1.11%-13.93%

