基于信息维数的加权网络分形特性分析
黄 毅,张 胜,戴维凯,王 硕,杨 芳
(南昌航空大学信息工程学院,南昌 330063)
0 引言
现实生活中广泛存在着的复杂系统都可以通过复杂网络来描述。对复杂网络拓扑特性的研究对于深入理解网络结构与网络行为之间的关系,并进而考虑改善网络的行为具有十分重要的意义,因此这也一直是复杂网络研究最重要的问题之一。1998—1999年,科学家们揭示了复杂网络的两大基本拓扑特性:小世界特性和无标度特性[1-2]。随后不久,2005年,Song等人[3]将重整化分析法和分形理论中的盒子覆盖法推广运用于复杂网络研究中,揭示了大量真实网络具有自相似性和分形特性,其中自相似性是指网络度分布的幂律形式及幂律指数在重整化过程中保持不变,而分形特性是指覆盖整个网络所需的最小盒子数量NB与盒子尺寸lB呈幂律关系,即NB≈lB-dB,dB为网络的分形维数。复杂网络分形特性的揭示有助于人们更加深入地理解网络结构的复杂性。同时,分形特性被誉为复杂网络的第三大基本拓扑特性,也因此成为了目前复杂网络研究的热点。
复杂网络分形特性研究的主要工作之一是计算网络的分形维数,分形维数不仅可以对网络的分形特性做出定量刻画,同时也可用于度量分形网络的鲁棒性[4]。最常见的计算网络分形维数的方法是盒子覆盖法[5]。盒子覆盖法最早是运用于计算欧式空间中传统分形体分形维数的方法[6],Song等人将这一方法推广运用于计算复杂网络的分形维数[3],其基本思想为:用尺寸为lB的盒子覆盖网络(一个盒子就是一组节点的集合,在此集合中任意两个节点间的距离小于lB),统计出覆盖整个网络所需的最少盒子数NB,然后增加盒子尺寸(逐次加1直到等于网络的直径),经多次实验后若lnNB与lnlB呈幂律关系则说明网络具有分形特性,其分形维数(也称盒维数)为拟合直线斜率的绝对值。盒子覆盖法可归结为如何找到规定盒子尺寸下覆盖整个网络所需的最小盒子数,这是一个NP难问题,只能尽可能求出最优解。Song等人[7]提出了3种经典的盒子覆盖算法:贪婪着色算法、紧凑盒子燃烧算法以及最大排除质量燃烧算法。在贪婪着色算法中,寻找网络的最小覆盖问题被映射为图论中的点着色问题,该算法最大的特点是具有较小的时间复杂度且易于实现,因此得到了广泛的应用。紧凑盒子燃烧算法能产生与贪婪着色算法相媲美的结果,但是不适用于分析异质网络的分形特性。最大排除质量燃烧算法则是通过计算节点的排除质量来找到网络的最小覆盖,因此往往能得到一个确定性解,但是该算法具有非常高的时间复杂度。随后,受Song等人[8]思想的启发,研究人员从提高计算效率和降低时间复杂度等角度提出了更多的盒子覆盖算法。例如Kim等提出了随机序列盒子覆盖算法,但该算法仍然具有较高的时间复杂度。Gao等[9]则对Kim提出的算法做了进一步改进,提出了等级驱动盒子覆盖算法。Sun等人[10]提出了重叠盒子覆盖算法,这种可重叠的盒子从某种意义上来说与现实网络中存在的重叠社区相吻合。此外,也有不少研究人员根据网络的现实特征从其他角度提出了一些盒子覆盖算法。如Zhang等人[11]从分形网络的中心节点具有排斥性的角度提出了基于库伦定律的盒子覆盖法。Wu等人[12]将最小化盒子数量与最大化分形模块度作为盒覆盖过程中的优化目标,提出了一种多目标优化的盒子覆盖法。
除了盒子覆盖算法定义的盒维数外,Shanker[13]提出了复杂网络体积维数的概念,其基本思想为任选节点i为中心节点,将半径r范围内覆盖到的节点数量定义为节点i的体积,然后遍历网络中的节点为中心节点,计算所有节点的体积和的平均值,记为V(r),通过改变r的取值,多次实验后测试V(r)与r是否满足幂律关系来判断网络是否具有分形特性。随后,Guo等人[14]在Shanker的基础上进一步提出了基于平均密度的体积维数。Wei等人[15]从考虑节点间差异性的角度进一步推广了体积维数的定义。Wang等人[16]提出了相关维数的概念,通过分析给定距离r下,任意两个节点间距离小于r的数量与网络节点对总数的比率之间的关系来分析网络的分形特性。与盒维数相比,相关维数的计算具有更小的时间复杂度。同时,Lacasa等人[17]还提出了基于遍历理论的相关维数。此外,Wei等人[18]考虑到盒子覆盖算法中每个盒子覆盖能力的差异性,提出了复杂网络信息维数的概念。Zhang等人[19]提出了基于非广延熵的复杂网络非广延信息维数。文献[20]在Wei等人提出的信息维数概念上,提出了基于最大熵最小覆盖的复杂网络信息维数。
以上的研究从不同的角度分析了复杂网络的分形特性。但是,值得注意的是,大多数研究只是针对无权网络。文献[21]提出了分析加权网络分形特性的改进盒子覆盖算法(Box-covering algorithm for weighted networks,BCANW),为研究加权网络的分形特性提供了一个非常好的思想。随后,文献[22]采用这种思想提出了分析加权网络多重分形特性的沙箱算法(Sandbox algorithm,SBW)。事实上,在SBW算法中,通过对广义分形维数D(q)取特殊值也能计算得到加权网络的分形维数(q=0时,D(0)为网络的盒维数)。但是,不同q值对应的D(q)值是通过选取实验曲线中合适的幂律范围然后对该范围进行线性拟合得到,而如何选取适合的幂律范围只是通过观察实验曲线,并无精确的数值方法,故这种通过取特殊值的方法来计算加权网络的分形维数与网络的实际维数值存在差别。加权网络能对复杂系统各单元间的相互作用提供更加细致的描述。因此,进一步完善有关加权网络的分形研究理论就显得至关重要。一些表面上很相似的维数定义,它们具有的性质可能差别很大,尤其是目前分形理论已经不局限于考察分形体结构的分形,而是扩展到从功能和信息等角度考察分形体的分形特性。为此,本文提出基于信息维数的加权网络分形特性分析方法(Information dimension algorithm for weighted networks,IDANW),从信息量的角度刻画加权网络的分形特性。
1 无权网络信息维数算法
信息维的概念是由Renyi基于概率理论提出。文献[23]将这一概念推广应用于复杂网络分形特性的研究。然而,该方法并不适用于计算实际网络的信息维数,原因在于该方法的核心思想是将复杂网络嵌入到一个平面上,然后用不同尺度的正方形格子分割此平面,但是真实系统抽象出的复杂网络模型往往不易于嵌入到一个平面上。Wei等人[18]提出的基于盒子覆盖算法的复杂网络信息维数改进算法则使得信息维在实际网络中具有可操作性而不再局限于构造网络。在盒子覆盖算法中,每个盒子被视为具有相同的覆盖能力。而在信息维的定义中,则充分考虑覆盖过程中每个盒子覆盖能力的差异性。具体的无权复杂网络信息维数的算法实现步骤可归纳为
1)对给定的网络G和盒子尺寸lB,利用盒子覆盖法找出网络的最小覆盖。
2)将所有的盒子进行编号,定义复杂网络落入第i个盒子的概率为
(1)
其中,n为网络节点总数,ni(lB)为盒子尺寸为lB时第i个盒子中包含的节点总数。基于这样一组概率值,计算该盒子尺寸下网络的信息熵:
(2)
综合式(1)和(2),可得到复杂网络信息维数的计算公式为
(3)
在实际计算中,由于盒子长度lB为离散值,无法实现lB→0,因此通常处理的方法是让盒子尺寸lB从1开始逐次加1直到等于网络直径,分别统计出每个盒子尺寸lB下对应的信息熵I(lB),然后线性拟合I(lB)~lnlB的直线,其斜率值即为信息维数dI的值。
2 加权网络信息维数算法
和无权网络相比,加权网络能更加细致地刻画网络的特征。例如在科学家合作网络中[24],两个科学家之间合作的次数越多,表明这两个科学家之间的关系越密切,倘若用无权网络刻画该网络,则会丢失很多重要信息。信息维数的计算首先基于盒子覆盖算法,而在盒子覆盖算法中,传统的盒子尺寸赋值规则是从1开始逐次加1直到等于网络的直径,这种赋值规则与无权网络中节点间距离的定义具有某种内在的关系。但是,加权网络中节点间距离的定义与无权网络并不一致,甚至存在一些加权网络的直径小于1。这说明传统的盒子尺寸赋值规则并不完全适用于加权网络。
2.1 算法思想
无权网络中任意两个节点间的距离定义为节点间的最短路径长度,也即连接这两个节点的最小边数,其距离值为正整数。加权网络中任意两个节点间的距离则和连接这两个节点的边的权重值有关,边权重值又可分为相异权和相似权两种相反的情况。相异权表示权重值越大,节点间的连接越疏远,距离也就越远;相似权意味着权重值越大,节点间的连接越紧密,距离也就越近。目前如何通过边权重值计算节点间距离值并无统一的标准,最常见的一种方法是Dijkstra算法。具体定义如下:
(4)
或者是:
(5)
其中,τ是节点i和j之间所有相连路径的集合。然而,该方法求出的节点间距离值往往是一个小数,且值很小,表明网络的直径也很小,这意味着在盒子覆盖算法中,盒子尺寸很快就能达到网络的直径,从而无法得到多组数据来描绘盒子尺寸与该尺寸下相应信息熵的关系,最终导致无法准确地刻画网络的分形特性。文献[21]提出的BCANW算法的核心思想是摒弃习惯上盒子长度为整数的想法,对直接相连的节点间距离值进行累加来给盒子尺寸赋值。实际上,这种赋值方式与传统的盒子尺寸赋值思想完全吻合,只是在传统的盒子尺寸赋值规则中,每次累加的基数为1,也即无权网络中直接相连的节点间距离值。受BCANW算法思想的启发,提出基于信息维数的加权网络分形特性分析方法,称为IDANW算法(Information dimension algorithm for weighted networks)。
2.2 算法步骤
IDANW算法步骤描述为
步骤1 对给定的加权复杂网络G,根据网络权重值表示的实际含义,计算网络中直接相连的节点间的距离值,并按从小到大的顺序排序,记为d1,d2,d3,…,dn。设置初始盒子尺寸lB=d1。
步骤2 对给定的盒子尺寸lB,利用贪婪着色算法找出网络的最小覆盖,并计算该尺寸下网络G的信息熵I(lB)。
步骤3 分别设置盒子尺寸lB=d1+d2,lB=d1+d2+d3,lB=d1+d2+d3+d4…,重复第二步,直到盒子尺寸lB大于等于网络的直径。统计出每个lB所对应的I(lB)。
步骤4 拟合I(lB)~lnlB。
考察拟合I(lB)~lnlB后的直线,若呈线性关系,说明加权复杂网络G具有分形特性,对应的信息维数即为拟合直线的斜率的绝对值。
3 实验结果及分析
本节分别采用IDANW算法来分析一类构造的加权网络和3个实际加权网络的分形特性。并且,在对实际加权网络分形特性的分析中,分别将网络看成无权网络和加权网络两种情况。
3.1 对构造加权网络的分析
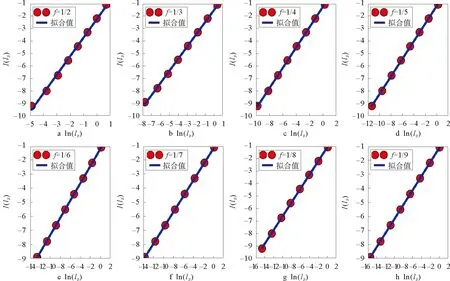
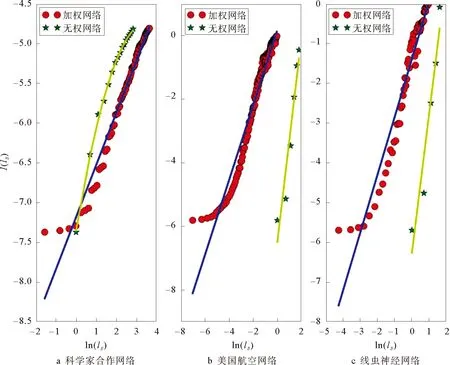
谢尔宾斯基(Sierpinski)加权分形网络是由Carletti等人提出,由迭代函数系统(Iterated Function Systems)生成,其生成过程由两个参数决定,分别是图形复制数目s(s>1)以及变化比例因子f(0 (6) 为了构造谢尔宾斯基加权分形网络,初始网络设置为单个节点,然后根据参数s和f的值,依次生成下一代网络。如图1表示s=3,f=1/2的谢尔宾斯基加权网络生成过程,其中G0由单个节点构成,将G0复制3次然后通过权重值为“1”的边连接起来得到G1,如此重复,后一次连接权重值为前一次的“1/2”倍,易知其自相似维数为lg3/lg2≈1.585 0。 s=3,f=1/2图1 “谢尔宾斯基”加权网络生成过程Fig.1 The growth process of sierpinski weighted networks with parameters 这里将图形复制数目s设置为3,比例变化因子f依次设置为1/2,1/3,1/4,1/5,1/6,1/7,1/8,1/9,然后利用IDANW算法计算每个f值下的谢尔宾斯基加权网络的信息维数。由于计算机处理能力有限,我们只生成第八代谢尔宾斯基加权分形网络,记为G8。G8具有9 841个节点和9 837条边。谢尔宾斯基加权分形网络的边权重值并无特殊的物理含义,因此可直接将边权重值视为连接这两个节点的距离值。当f=1/2时,盒子尺寸分别设置为1/128,1/128+1/64,1/128+1/64+1/32,…,1/128+1/64+1/32+1/16+1/8+1/4+1/2+1,然后计算相应的信息熵并对所得数据进行拟合,结果如图2a所示。同理设置其余值下的盒子尺寸并计算相应信息熵,结果如图2b-2h所示。 图2 第八代谢尔宾斯基加权网络的分形特性分析Fig.2 Fractal scaling analysis of the eighth generation of sierpinski weighted networks 图3 s=3,-lg(3)/lg(f)的理论曲线与不同f值对应的信息维数Fig.3 When s=3, the theoretical curve of -lg(3)/lg(f) and the information dimensions with respect to different values of f 从图2可以看出,每个值下的盒子尺寸与相应信息熵均能够很好拟合成一条直线,拟合直线的斜率即为信息维数的值。当而取不同值时,谢尔宾斯基加权分形网络的理论维数值可由式(7)计算 (7) 为此,分别计算每个f值对应的理论维数值,并与实际计算的信息维数值进行比较。结果如图3和表1所示。 从图3和表1可看出,当变化比例因子f取不同值时,IDANW算法计算所得的信息维数值与谢尔宾斯基加权分形网络的理论维数值十分接近,最大相对误差为5.93%,这也表明了IDANW算法在分析构造加权网络分形特性时的有效性。 进一步地,利用IDANW算法分析3个更具代表性的实际加权网络的分形特性。分别是Newman科学家合作网络[24],美国航空网络(数据源:http://vlado.fmf.unilj.si/pub/networks/data/)以及线虫神经网络[1]。这3个实际网络的盒维数已在文献[21]中计算得到。 表1 s=3,不同f值对应的信息维数与理论维数Tab.1 The information dimensions and the theoretical dimensions of sierpinski weighted networks with parameter s=3 and different values of f Newman科学家合作网络具有1 589个节点与2 742条边,其中节点代表科学家,边代表两个科学家之间具有合作关系。节点i和节点j之间权重值的计算方法为 (8) 美国航空网络是将332个机场抽象为网络节点,2 126条航班抽象为边的网络。网络的权重值是指定期航班的客容量(单位:百万人次/年)。显然,当权重值越大时,表示两个机场关系密切,距离就越近(这里的距离并非指两个机场之间的地理距离),因此美国航空网络的权重类型也是相似权。采用式(5)计算网络中节点间距离后得到网络的直径为0.96。若采用传统的盒子尺寸赋值思想,覆盖整个网络只需一个盒子,相应的信息熵为0,因此无法利用信息维数刻画该网络的分形特性。同样地,分别将美国航空网络视为加权网络和无权网络两种情况并分析其分形特性。结果如图4b所示。从图4b可以看出,无权航空网络和加权航空网络均表现出分形特性,其信息维数分别为3.218和1.179。 图4 IDANW算法分析实际加权网络Fig.4 Fractal scaling analysis of real-world networks by IDANW 线虫神经网络具有306个节点和2 148条边,节点表示神经元,边表示神经元之间的连接,边的权重值由神经元之间的连接强度决定。当连接强度越大时权重值也越大,表明两个神经元关系密切,距离就越近,因此线虫神经网络的权重类型仍然是相似权。对无权线虫神经网络和加权线虫神经网络分形特性的分析结果如图4c所示。从图4c可以看出,无权线虫神经网络和加权线虫神经网络也均表现出分形特性,其信息维数分别为3.505和1.458。 通过对3个不同实际加权网络的分析可以看出,当把网络看成无权网络和加权网络两种情况时,两者的信息维数并不一致,这说明加权网络的边权重值对网络的分形特性具有一定的影响。更进一步地,采用BCANW算法分析上述3个实际加权网络的分形特性,并将分析结果与IDANW算法得到的结果进行对比。同样,分别将网络看成加权网络和无权网络两种情况。采用BCANW算法分析的结果如图4中红色圆点所示,对比结果如表2所示。 图5 BCANW算法分析实际加权网络Fig.5 Fractal scaling analysis of real-world network by BCANW 算法分形维数科学家合作网络美国航空网络线虫神经网络IDANW加权信息维数0.6551.1791.458无权信息维数无分形特性3.2183.505BCANW加权盒维数0.3461.0080.826无权盒维数无分形特性3.1193.331 从图5和表2可以看出,当利用盒维数分析这3个实际网络的分形特性时,加权科学家合作网络的盒维数为0.346,而无权科学家合作网络则没有表现出分形特性。对于美国航空网络,加权美国航空网络和无权美国航空网络均表现出分形特性,其盒维数分别为1.008和3.119。对于线虫神经网络,加权线虫神经网络和无权线虫神经网络的盒维数分别为0.826和3.331。注意到,对不同的实际网络,IDANW算法和BCANW算法计算所得的分形维数值差异性表现差别较大。对于科学家合作网络和美国航空网络,IDANW算法和BCANW算法计算所得的分形维数值较为接近,差值分别为0.309和0.171。而对于线虫神经网络,二者的差值较大,为0.632。实质上,IDANW算法和BCANW算法是对同一个网络,从不同的角度去分析它的分形特性,其中BCANW算法是从盒子尺寸与该尺寸下盒子数量间的关系分析网络的分形特征,而IDANW算法则是从盒子尺寸与该尺寸下网络信息熵间的关系来分析网络的分形特征,所以两种方法计算求得的维数值也不同。 为了考察直线的拟合效果和进一步比较IDANW算法和BCANW算法,这里考虑最小二乘拟合法的均方误差值Q,其定义为 (9) 表3 IDANW算法和BCANW算法拟合结果对比Tab.3 The fitting results comparison between IDANW and BCANW 从表3可以看出,科学家合作网络和美国航空网络的均方误差值都比较小,用IDANW算法和BCANW算法均能发现其具有分形特性。对于线虫神经网络,IDANW算法的均方误差较小,为0.419 5,而BCANW算法的均方误差值则达到0.735 0,接近于1。表2中表明对于线虫神经网络用IDANW算法和BCANW算法分析其分形特征时,两个方法的结果差异比较明显,并且从图5c中也能发现其数据点较为分散,这说明加权线虫神经网络的分形特性用BCANW算法不易度量出。此外,从表3也能看出,Q1的值要比Qb的值小,这也进一步表明了IDANW算法在分析实际加权网络分形特性时的有效性。 复杂网络信息维数实质是香农熵的一种表现形式。本文针对目前网络分形研究主要针对无权网络这一问题,提出了一种基于信息维数的加权网络分形特性分析方法(IDANW)。通过对一类构造的谢尔宾斯基加权网络和3个实际加权网络的分形分析结果表明了IDANW算法能够较好度量出加权网络的分形特征。此外,在对实际网络的分形特性分析中,分别将网络看成加权网络和无权网络两种情况,结果发现加权网络的信息维数值与无权网络的信息维数值并不一致,表明网络权重值对网络分形特征有一定影响,这一结论与文献[21]和文献[22]所得结论一致。加权网络可以对复杂系统的相互作用结构提供更加细致的刻画。因此加权网络分形分析理论的建立有助于去分析实际加权网络中的统计特性从而更好地认识复杂系统。本文的研究进一步丰富了复杂网络分形的研究成果。

3.2 对实际加权网络的分析






4 结论

