电网输电线路耦合强度分配策略研究

陈思谕，邹艳丽，王瑞瑞，谭华珍

(广西师范大学电子工程学院, 广西 桂林 541004)

0 引言

在复杂网络的研究进程中，学者们发现网络[1-2]均以特定的耦合方式连接而成，并具有某些具体的功能，而网络的同步和稳定现象主要由节点间的耦合效应引起，因此耦合网络的动力学行为研究引起了学者们的极大关注[3-22]。

电网是一种常见的人工复杂网络，在电力网络研究中，通常设定网络中各连边耦合强度相等[6-14]，并从电网动力学建模[6-7]、电网故障[8]、分布式电站入网[9]，关键环节识别[10-12]、同步和稳定性分析[13-15]等方面进行深入研究。在电网耦合差异[15-18]研究方面，文献[16]研究了不同耦合方式和耦合强度对电力-通信网络的影响，研究表明，自相似耦合有利于提高电力-通信网络的稳定性，且以介数-度数耦合方式最佳。文献[17]综合考虑发电机和负载的动力学特性，根据能量守恒定律，推导出电力网络的动态负荷模型，模型从线路阻抗角度反映线路耦合差异。文献[18]基于类Kuramoto相振子模型，从动力学角度定义了电网边缘敏感度，并对系统单边耦合强度受到微小扰动时，系统响应方程进行了详细推导，得出了电网受单边耦合扰动的敏感度影响与相应边负载成正比的结论。文献[19]采用随机、同配、异配三种不同连边耦合方式构建相依网络，并从相依网络级联故障角度进行了深入研究。从输电线路耦合强度差异角度对电力网络同步和稳定性动力学行为的研究还比较少见。

本文考虑电力网络输电线路的耦合特性差异，提出3种电网输电线路耦合强度分配策略(EQ，TP，LB)。第一，各线路耦合强度相等，简称EQ方式；第二，各线路耦合强度按系统等耦合强度同步运行状态下，线路传输功率的绝对值大小正比分配，简称TP方式；第三，线路耦合强度按连边介数大小正比分配，简称LB方式。并从电网的同步和稳定性两个方面比较3种输电线路耦合强度分配策略的优劣。

1 电网动力学模型

考虑节点动力学特性的二阶类Kuramoto模型[7]被广泛应用于电力网络的同步和稳定性研究。此模型的数学表达式如下：

(1)

式中，N为网络节点个数，φi为节点i的相位偏差，Pi为节点i的功率，当节点i为发电机时，Pi>0，表示发电机节点提供功率，当节点i为负载时，Pi<0，表示负载节点消耗功率，α为损耗参量，K表示节点间的耦合强度，{aij}表示网络的邻接矩阵，描述网络的拓扑结构，若节点i与节点j之间有连边，则aij=aji=1，否则aij=0。

本文中仿真模型参数设置为：令负载节点功率Pc=-1，发电机节点功率Pg=-(Nc*Pc)/Ng，其中Ng、Nc分别为电网中发电机节点数和负载节点数，取系统中各节点的初始相偏、频偏均为0，我们采用经典四阶-龙格库塔积分法进行仿真计算，积分步长h=0.001，损耗参数α=0.1。

2 电网动力学性能评价指标

2.1 稳态序参数

在类Kuramoto模型中，电力网络被描述为耦合相振子网络，学者们通常采用相位序参数[20]来描述相振子网络的同步性能，其定义式为：

(2)

式中，θj(t)为相振子i的相位，φ(t)为网络中所有相振子的平均相位，N为网络中相振子个数，序参数r(t)可以反映不同时刻网络振子的同步情况。稳态序参数r∞表示网络运行到稳定状态后，一段平稳状态下序参数r(t)的平均值，其数学表达式为：

(3)

在电力网络中，当系统运行到稳定状态后，若r∞≈0，网络中无节点处于同步状态；r∞≈1，网络中所有节点处于同步状态。

2.2 临界同步耦合强度

在类Kuramoto模型中，当电力网络节点间的耦合强度K达到一定强度Kc时，系统能够同步运行，此时电网各节点频偏ωi=0；当耦合强度K小于Kc时，此时电网各节点频偏ωi≠0，系统运行在非同步状态。我们把电网刚好能同步运行的耦合强度称为临界同步耦合强度，用Kc表示，Kc越小，表明电力网络的同步能力越好。根据文献[7]的分析，耦合强度K正比于节点间的最大传输线容量pMAX，因此Kc越小，意味着我们可以用更小的传输线容量使电网同步运行，降低成本，提高性能；同时，一般电网的同步性能越好，其抗干扰能力越强，电网越稳定。

2.3 最大抗扰强度

在电网稳定性研究中，学者们通常采用电网运行在同步状态下，对系统各节点施加短暂功率干扰ΔP，在撤除干扰后系统仍能恢复同步运行状态的最大扰动强度ΔPmax来描述电网的稳定性能，ΔPmax越大，系统稳定性越好。

3 电网输电线路耦合强度分配策略

3.1 耦合强度按线路传输功率正比分配策略

根据电力网络的二阶类Kuramoto模型，可以将式(1)改写为式(4)的两个一阶微分方程：

(4)

当电力网络运行在同步状态时，系统运行在标准频率(50HZ或60HZ)，所有节点频偏为零，即ω1=ω2=…=ωN=0，其中N为系统节点数。那么，由式(4)可得：

(5)

根据式(5)，系统运行在同步稳定状态时，节点i、节点j间的连边eij的传输功率设为：

Pij=Kaijsin(φj-φi)，i,j=1,2,…N

(6)

将线路耦合强度按照电网传输线功率大小重新分配，得到系统动力学方程为：

(7)

3.2 耦合强度按边介数正比分配策略

边介数Bij是网络的一个全局特征量[2]，可以用来评价网络中连边的重要性，一般认为介数越大，该边在网络中越重要。其数学表达式为：

(8)

式中，Nlm为从节点l到节点m的最短路径条数，Nlm(eij)为从节点l到节点m的最短路径中经过连边eij的最短路径条数。

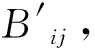
(9)

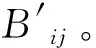
4 IEEE标准网络上三种分配策略比较研究

本节研究内容主要在IEEE14、IEEE30、IEEE39、IEEE57节点系统进行仿真实验，并从电网的同步性能和稳定性两个方面进行仿真分析，比较三种线路耦合强度分配策略的优劣。在IEEE标准测试系统中，IEEE14系统由5个发电机节点、9个负载节点和20条连边构成；IEEE30系统由6个发电机节点、24个负载节点和41条连边构成；IEEE39系统由10个发电机节点、29个负载节点和46条连边构成；IEEE57系统由7个发电机节点、50个负载节点和78条连边构成。

4.1 IEEE网络上三种耦合方式的同步性能比较

在电网的同步性能研究中，本文通过临界同步耦合强度Kc来反映系统同步性能，并从系统同步性能的角度对三种输电线路耦合强度分配策略进行比较。

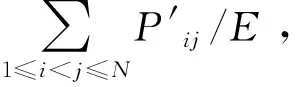
图1 IEEE14系统稳态序参数r∞、平均频偏ω∞和平均耦合强度〈K〉的关系Fig.1 The relationship between steady state order parameter r∞, average frequency offset ω∞ and average coupling strength of IEEE14 system

图2 IEEE30系统稳态序参数r∞、平均频偏ω∞和平均耦合强度〈K〉的关系Fig.2 The relationship between steady state order parameter r∞, average frequency offset ω∞ and average coupling strength of IEEE30 system

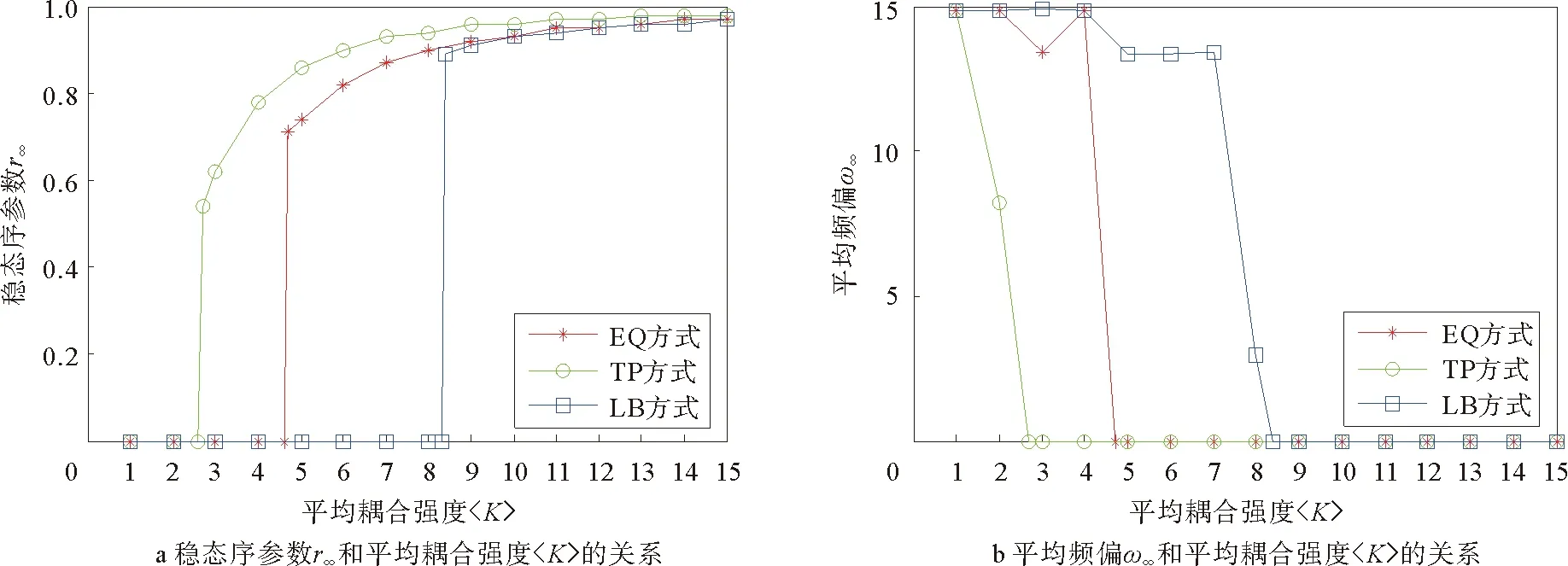
图3 IEEE39系统稳态序参数r∞、平均频偏ω∞和平均耦合强度〈K〉的关系Fig.3 The relationship between steady state order parameter r∞, average frequency offset ω∞ and average coupling strength of IEEE39 system

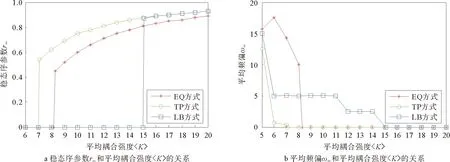
图4 IEEE57系统稳态序参数r∞、平均频偏ω∞和平均耦合强度〈K〉的关系Fig.4 The relationship between steady state order parameter r∞, average frequency offset ω∞ and average coupling strength of IEEE57 system

由仿真计算求得，在IEEE14系统中，KEQ=2.3，KTP=1.7，KLB=2.5；在IEEE30系统中，KEQ=5.9，KTP=3.4，KLB=7.3；在IEEE39系统中，KEQ=4.7，KTP=2.7，KLB=8.4；在IEEE57系统中，KEQ=8.3，KTP=7.1，KLB=15.1；从图1至图4可以看出，当系统平均耦合强度〈K〉大于等于相应平均临界同步耦合强度时，系统平均频偏ωi=0，电网同步运行；当系统平均耦合强度〈K〉小于相应平均临界同步耦合强度时，系统平均频偏ω∞≠0，电网运行在失同步状态。仿真结果表明，在以上各IEEE标准系统中，输电线路耦合强度按TP方式分配时，系统平均临界同步耦合强度KTP最小，系统同步性能最好；按LB方式分配时，系统平均临界同步耦合强度KLB最大，系统同步性能最差；按EQ方式分配时，系统平均临界同步耦合强度为KEQ大于KTP而小于KLB，系统同步性能介于两者之间。

4.2 IEEE网络上三种耦合方式的稳定性能比较

在电网稳定性研究中，通常采用电网同步运行状态下，系统能承受的最大干扰功率ΔPmax来描述电力网络的稳定性能，ΔPmax越大，系统抗扰能力越强，稳定性越好。为比较电力网络在三种输电线路耦合强度分配策略下的稳定性能，取系统平均耦合强度〈K〉相等，且〈K〉>{KEQ,KTP,KLB}，保证系统运行在同步状态，研究各方式下，系统抗扰能力随系统平均耦合强度〈K〉的变化情况。当系统运行到稳定状态一段时间后，对每个负荷节点施加扰动功率ΔP，扰动持续时间Δt=5s，仿真结果如图5所示。

由图5可以看出，在各电力系统中，三种耦合方式下，系统最大抗扰值ΔPmax均随着系统平均耦合强度〈K〉的增大而增大，即系统稳定性均随着系统平均耦合强度〈K〉的增大而增强。当系统平均耦合强度〈K〉相等时，TP方式下，系统能够承受的最大抗扰强度ΔPTPmax最大；LB方式下，系统能够承受的最大抗扰强度ΔPLBmax最小；EQ方式下，系统能够承受的最大抗扰强度ΔPEQmax介于两者之间。由仿真结果可知，输电线路耦合强度按TP方式分配时，系统抗扰性能最好，稳定性最佳；按LB方式分配时，系统抗扰性能最差，稳定性最差；按EQ方式分配时，系统抗扰性能介于两者之间，即系统稳定性介于两者之间。

图5 三种耦合方式下最大抗扰强度ΔPmax与平均耦合强度〈K〉的关系Fig.5 The relationship between the maximum intensity of the disturbance ΔPmax and average coupling strength K in three coupled modes

5 小世界和无标度网络上三种分配策略比较研究

根据文献[21-22]的综述，绝大多数实际电力网络是具有较大聚集系数、较小平均路径长度的稀疏网络，具有小世界特性。由于电力网络正向大规模，复杂化的方向演化，以往的研究中既有用小世界网络对电网进行建模研究的，也有用无标度网络进行建模研究的，因此本文应用NW小世界网络模型和BA无标度网络模型构建电网拓扑模型，并进行仿真分析，进一步验证本文提出的三种输电线路耦合强度分配策略的科学性。

构建NW小世界电网模型[2]：令网络节点总数N=200，每个节点分别与它左右相邻的d/2个节点相连，其中d=4，任意一对节点之间，随机加边的连接概率p=0.01，该电网模型表示为NW_200。

构建BA无标度电网模型[2]：令网络节点总数N=200，初始节点m0=2构成连通图，每引入一个新节点，与网络中已存在的m=2个节点相连，该电网模型表示为BA_200。

本节将采用类Kuramoto模型对NW_200与BA_200系统进行动力学建模，并从电网的同步和稳定性两个方面进行仿真分析，比较三种输电线路耦合强度分配策略的优劣。在NW_200与BA_200网络中，随机取20个节点作为发电机节点，剩余节点为负荷节点，令负载节点功率为Pc=-1，根据电网生产和消耗功率平衡，发电机节点功率为Pg=-(Nc*Pc)/Ng，其中Ng=20为发电机节点个数，Nc=180为负载节点个数。

5.1 小世界和无标度网络上三种耦合方式的同步性能比较

本节将从电网的同步性能角度比较三种输电线路耦合强度分配策略的优劣。如3.1节所述，EQ、TP、LB三种线路耦合方式下，系统平均临界同步耦合强度分别用KEQ、KTP、KLB表示。通过仿真实验计算出三种耦合方式下，各系统平均临界同步耦合强度，并绘制出电网稳态序参数r∞、系统平均频偏ω∞随系统平均耦合强度〈K〉变化的图像。仿真结果如图6、图7所示：

图7 BA_200系统稳态序参数r∞、平均频偏ω∞和平均耦合强度〈K〉的关系Fig.7 The relationship between steady state order parameter r∞, average frequency offset ω∞ and the average coupling strength of the BA_200 system

由仿真计算求得，在NW_200系统中，KEQ=1.4，KTP=0.33，KLB=1.84；在BA_200系统中，KEQ=6.9，KTP=1.74，KLB=10.31；从图6、图7可以看出，当系统平均耦合强度〈K〉大于等于相应平均临界同步耦合强度时，系统平均频偏ω∞=0，电网同步运行；当系统平均耦合强度〈K〉小于相应平均临界同步耦合强度时，系统平均频偏ω∞≠0，电网运行在失同步状态。仿真结果表明，在以上两种网络模型电网中，输电线路耦合强度按TP方式分配时，系统平均临界同步耦合强度KTP最小，电网同步性能最好；按LB方式分配时，系统平均临界同步耦合强度KLB最大，电网同步性能最差；按EQ方式分配时，系统平均临界同步耦合强度KEQ大于KTP而小于KLB，电网同步性能介于两者之间。为验证本文提出的三种耦合策略的科学性，将各系统平均临界同步耦合强度以表格的形式列出，如表1所示。

表1 三种耦合方式下各系统平均临界同步耦合强度〈K〉Tab.1 The average critical synchronous coupling strength 〈K〉 of several systems under three coupling modes

由表1可知，以上各仿真系统的同步性能仿真结论具有一致性，即输电线路耦合强度按TP方式分配时，系统平均临界同步耦合强度KTP最小，电网同步性能最好；按LB方式分配时，系统平均临界同步耦合强度KLB最大，电网同步性能最差；按EQ方式分配时，系统平均临界同步耦合强度KEQ大于KTP而小于KLB，电网同步性能介于两者之间。

5.2 小世界和无标度网络上三种耦合方式的稳定性能比较

本节将从电网的稳定性能角度比较三种输电线路耦合强度分配策略的优劣，并用系统同步稳定运行状态下，系统能够承受的最大抗扰强度ΔPmax来描述电力网络的稳定性能。为比较电力网络在三种输电线路耦合强度分配策略下的稳定性能，取系统平均耦合强度〈K〉相等，且〈K〉>{KEQ,KTP,KLB}，保证系统运行在同步状态，研究系统抗扰能力随平均耦合强度〈K〉的变化情况。当系统运行到稳定状态一段时间后，对每个负荷节点施加扰动功率ΔP，扰动持续时间Δt=5s，仿真结果如图8所示。

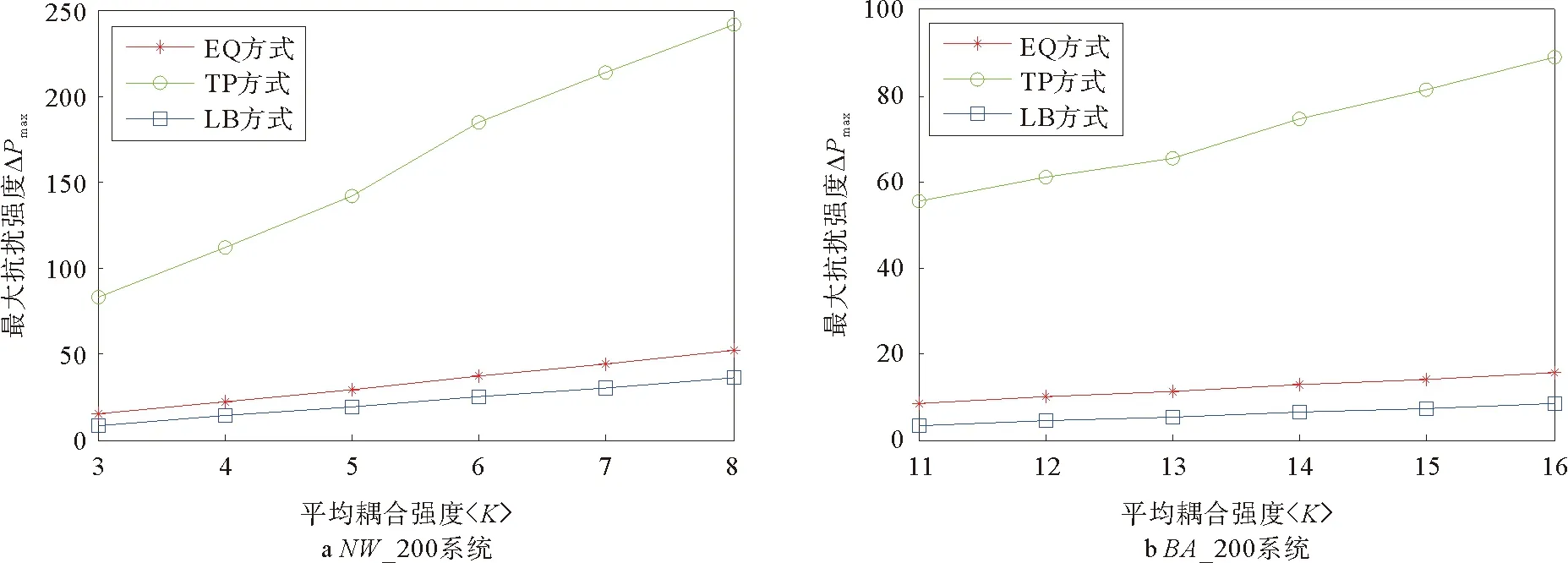
图8 三种耦合方式下最大抗扰强度ΔPmax与平均耦合强度〈K〉的关系Fig.8 The relationship between the maximum intensity of the disturbance ΔPmax and average coupling strength 〈K〉 in three coupled modes

由图8可以看出，在NW_200和BA_200系统中，三种耦合强度分配方式下，系统最大抗扰强度ΔPmax均随着平均耦合强度〈K〉的增大而增大，即系统稳定性均随着平均耦合强度〈K〉的增大而增强。当系统平均耦合强度〈K〉相等时，TP方式下，系统能够承受的最大抗扰强度ΔPTPmax最大；LB方式下，系统能够承受的最大抗扰强度ΔPLBmax最小；EQ方式下，系统能够承受的最大抗扰强度ΔPEQmax介于两者之间。由仿真结果可知，输电线路耦合强度按TP方式分配时，系统抗扰性能最好，稳定性最佳；按LB方式分配时，系统抗扰性能最差，稳定性最差；按EQ方式分配时，系统抗扰性能介于两者之间，稳定性介于两者之间。因此，两种网络模型上，系统的稳定性能仿真结论与IEEE标准网络一致。

本文的研究表明，对于高功率负载连边，赋予较大的耦合强度是有利于网络的同步和稳定性的，但对于高介数连边，赋予较大的耦合强度却会弱化网络的同步和稳定性，因此电网作为能量传输网络，一般情况下功率参数比结构参数包含更多信息，因而更重要。

6 结论

本文提出三种电力网络输电线路耦合强度分配策略，我们采用类Kuramoto模型对电力网络进行动力学建模，研究三种输电线路耦合强度分配策略下电力网络的同步和稳定性能的优劣，寻求更佳的线路耦合强度分配方案，以提高电力网络的同步和稳定性能。通过在IEEE标准测试网络、NW小世界网络和BA无标度网络进行仿真实验，研究表明输电线路耦合强度按等耦合强度下传输功率大小重新分配时(TP方式)，电网的同步和稳定性能皆为最佳；按传输线路介数大小分配耦合强度时(LB方式)，电网的同步和稳定性能均为最差；所有传输线路耦合强度相等时，电力网络的同步和稳定性能均优于LB方式，而劣于TP方式。本文的研究对于未来电网的改造具有一定指导意义。