基于复杂网络的差分进化算法研究
丁 毓,刘三阳,陈静静,白艺光
(西安电子科技大学数学与统计学院,西安 710126)
0 引言
差分进化算法(Differential Evolution,DE)是一种简单且有效的启发式方法,用于求解连续空间问题的全局最优解。该算法是R.Storn和K.Price[1-2]于1995年,为求Chebyshev多项式而提出的,后来发现DE也是解决复杂优化问题的有效工具。
进化算法在科研和实际问题中的应用十分广泛,研究人员提出多种不同的进化方法,其中包括群智能进化方法研究与应用[6-8],随着对进化算法的研究,进化算法与复杂网络[9-10]的联系逐渐被挖掘,既可用进化算法解决网络中的问题,也可将网络作为设计进化算法的工具。如Ashlock[11]等人在1999年提出了采用组合图来限制杂交对象选择的遗传算法;Mabu[12]等人在2007年提出了基于图的进化算法和基于图的强化学习算法;Zelinka[13-14]等在2010和2011年提出可视化进化算法的动力学模型;2017年Skanderova等[15]提出利用复杂网络对进化算法进行动力学分析。
2017年,Benjamin等[16]发表的文章说明种群结构会影响种群最终的进化结果,受Skanderova[15]启发,采用将算法中的种群结构记录为复杂网络的方法,用网络所含信息指导种群进化,提出基于复杂网络的差分进化算法(Differential Evolution Algorithm Based on Complex Networks,CNDE)。该算法将差分进化算法中的种群对应网络,给种群中的个体匹配网络中的节点,用边来表示个体之间的关系。利用网络的信息,得出个体基因组好坏的相关参数信息。接着,利用目标函数值和个体基因组信息共同决定个体被选择为突变算子中目标向量的概率。在计算概率时,为了保证算法的稳定性,提升收敛速度,引入收敛因子α。在选择阶段,针对差分进化算法中的交叉与变异机制,提出新的基于排序的选择模式,从而优化子代的种群结构。
1 标准差分进化算法
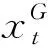
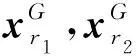
(1)
其中,指标r1,r2,r3∈{1,2,…,NP},且r1,r2,r3,t全不相同。尺度因子F是一个正的实常数,一般F∈[0,2]。
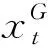
(2)
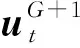
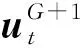
(3)
2 基于复杂网络的差分进化算法
根据达尔文进化论:好的基因组更容易被传播下来。个体能够多次成功地产生后代,则认为该个体具有较好的基因组。因此种群中目标向量的选择可以结合种群的基因组信息。而复杂网络可视化了个体在种群中的关系,提供了个体的基因组信息,为进化算法的研究提供了一个新的视角。
2.1 网络的构造
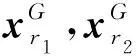
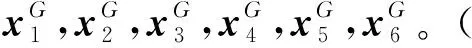
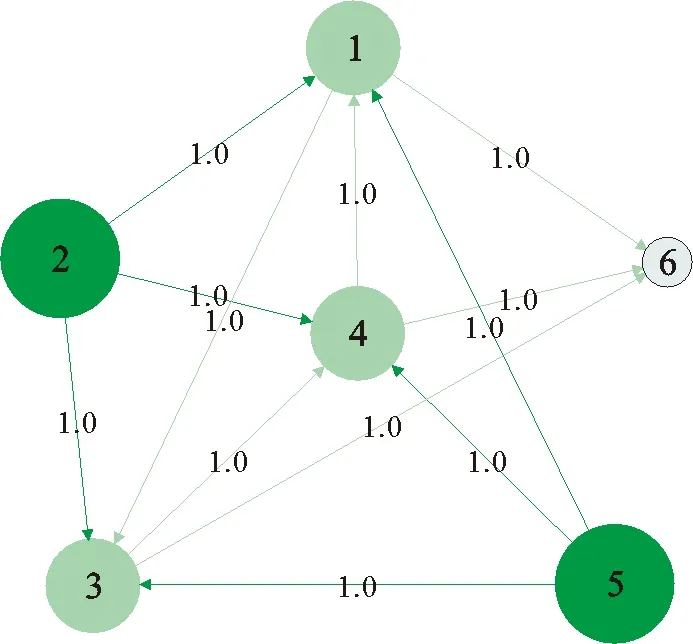
图1 差分进化算法第一代网络Fig.1 The first generation network of differential evolution algorithm
假设第二代成功进化的个体及其父代记录如下x4:{x2,x3,x5},x6:{x2,x3,x4}。根据记录,更新第二代的网络,如图2所示,并更新邻接矩阵A2:
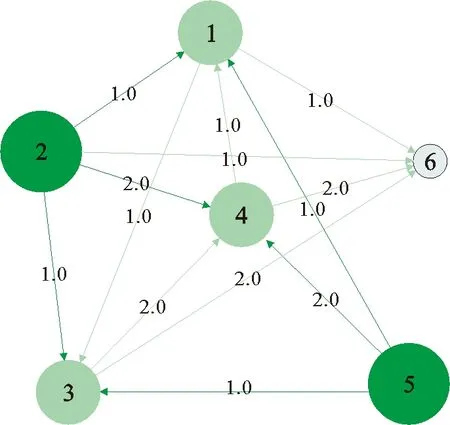
图2 差分进化算法第二代网络Fig.2 The second generation network of differential evolution algorithm
接下来的每一代都用相同的方法更新网络。当个体数目足够多,进化代数越来越大时,网络结构也将变得越来越复杂。
2.2 变异策略的改进
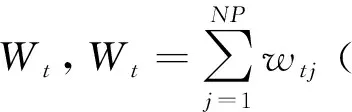
1)赋权有向边能够获取从一个节点到另一个节点的基因组的传播信息。
2)节点的出边加权和Wt,表示该节点成功作为父代的次数,次数越多表明基因组越好。
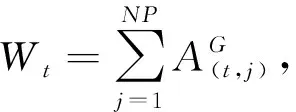
随着每代邻接矩阵AG建立,每个节点的出边加权和便可求出。接着,根据式(4)计算出个体被选择为目标向量的概率:
(4)
式(4)表明,具有较高出边加权和的个体,在突变算子中被选为目标向量的可能性高。特别地,在式(4)中对每个个体的选择概率都加α,这里α称作收敛因子,其作用一是为了保证算法的稳定性,便于控制收敛速度,二是为了消除选择概率为零的情况,避免降低目标向量的多样性。α通常取值为1,可根据不同的函数类型调整α的大小,一般情况下,对连续的单峰函数,将α取较小值,加速收敛;对于不可分的多峰函数,将α取较大值,增加种群的多样性。通过实验,发现α的取值对算法的稳定性有较大的影响,且不同的函数对α的要求也不同。本文收敛因子α的取值是通过实验测试选取,日后可研究对不同类型的函数自适应设置α的取值。
式(4)只考虑了基因组好的个体在突变算子中被选择作为目标向量的可能性较高。但是,除此之外本文还应考虑目标函数值好的个体,因为目标函数值好,不一定成功进化的次数多。因此更新个体被选为目标向量的概率为
(5)
其中,pbest表示目标函数值最好的个体在突变算子中被选为目标向量的概率。
推荐理由:本书是华尔街投资大神、对冲基金公司桥水创始人瑞·达利欧的人生经验之作,是他白手起家40多年以来的生活和工作原则。书中提到了21条高原则、139条中原则、365条分原则,多角度、立体阐述了生活、工作、管理原则。在中国金融圈、投资界和管理层都极具影响力,在中国大陆销量达一百万册,适合多层次、多领域的读者阅读。
2.3 选择策略的改进
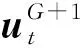
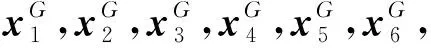
如果使用标准差分进化算法的选择算子则第G+1代个体选择如下:
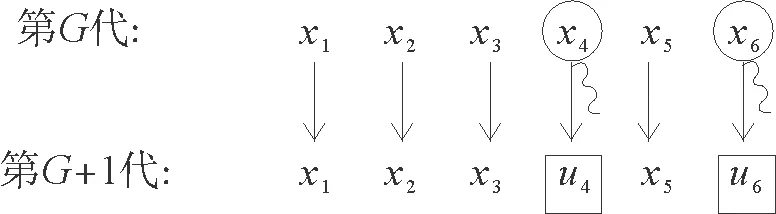
而如果使用基于目标函数值排序的选择策略,那么第G+1代个体选择如下:
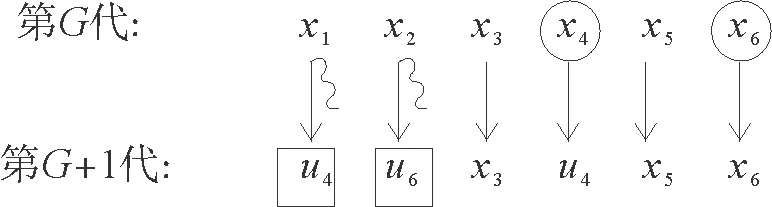
由假设条件可知f(x1)≥f(x2)≥f(x3)≥f(x4)≥f(x5)≥f(x6),且满足条件f(u4) 基于复杂网络的差分进化算法的基本思路是:首先随机初始化种群、网络,对于第一代个体,其变异算子采用标准差分进化算法的方法。对于第二代及以后个体则利用网络的性质计算基因组好坏参数。在变异阶段依概率选取目标向量,概率由个体的目标函数值大小基因组信息计算得出。选择阶段采用基于目标函数值排序的策略。其具体实现步骤如下: Step 1:初始化,设定相关符号说明如下表1所示: 表1 算法符号说明Tab.1 Algorithm symbol description 此外,用Tab表示个体成功进化标记,初始化Tab=zeros(1,NP),如果第t个个体成功进化,记Tab的第t个分量为1,否则记为0。 Step 2:在可行域中随机生成NP个D维个体,计算对应目标函数值。 Step 3:对Tab进行更新,Tab=zeros(1,NP);对目标函数值从大到小排序;对目标函数值最小的个体,根据式5)计算概率。 Step 4:变异操作,如果∑Wt=0则按标准差分进化算法执行变异算子,否则根据计算出来的概率依概率选择目标向量。并将个体对应的父代记录在集合S中。 Step 5:根据式(2)生成试验向量,并计算试验向量的目标函数值。 Step 7:求出Tab等于1的个数k,将这k个试验向量替换目标函数值最大的k个目标向量。 Step 8:根据S矩阵计算邻接矩阵A,由式(4)和(5)利用目标函数值大小和基因组信息计算每个节点的选择概率pt。 Step 9:判断是否满足终止条件,若不满足转Step3。 为了测试基于复杂网络的差分进化算法(CNDE)的性能,用21个标准测试函数[17]进行测试,算法由matlab软件实现。表2给出了测试函数的名称、维数、搜索空间和理论最优值。其中:f1~f13为高维问题,f1~f7为单峰函数,f8~f13为多峰函数,f14~f21为低维函数。 表2 测试函数的名称、维数、搜索空间和最优值Tab.2 The name, dimension, search space, and optimal value of the test functions 续表2 函数名称维数搜索空间最优值函数名称维数搜索空间最优值f6Step30[-100,100]0f17Branin2[-5,10],[0,15]0.398f7Quartic30[-1.28,1.28]0f18Goldstein2[-2,2]3f8Schwefel 2.2630[-500,500]-12 569.5f19Shekel 14[0,10]-10.153 2f9Rastrigin30[-0.512,5.12]0f20Shekel 24[0,10]-10.402 9f10Ackley30[-32,32]0f21Shekel 34[0,10]-10.534 0f11Griewank30[-600,600]0 在本文测试中,各参数取值如下:种群规模NP=100;尺度因子F=0.6;杂交概率CR=0.9;对于不同函数,收敛因子α和最大迭代次数G的取值见表3。 表3 部分参数取值表Tab.3 Parameter value table 因本文是受启于lenka skanderova在2017年[13]提出的enhanced DE算法,故将本文算法与enhanced DE算法进行对比,两个算法分别独立运行50次,测试结果如表4所示。其中best表示50次独立运行的最好值;worst表示50次独立运行的最差值;Mean表示平均值,反映了算法的求解精确度;S.D表示标准差,反映了算法的稳定性。 表4 Enhanced DE与CNDE对21个函数的测试结果比较Tab.4 Enhanced DE compared with CNDE test results for 21 functions 续表4 函数算法BestWorstMeanS.Df10Enhanced DE2.920×10-063.872×10-048.573×10-051.930×10-04CNDE8.033×10-113.096×10-074.938×10-086.203×10-08f11Enhanced DE7.772×10-152.396×10-021.074×10-033.520×10-03CNDE01.478×10-022.563×10-044.340×10-03f12Enhanced DE1.879×10-112.388×10-061.366×10-084.351×10-09CNDE1.826×10-162.115×10-102.532×10-125.108×10-11f13Enhanced DE1.347×10-108.932×10-021.327×10-022.498×10-02CNDE3.549×10-212.972×10-141.495×10-155.686×10-15f14Enhanced DE0.998 003 82.982 105 11.057 566 42.459CNDE0.998 003 80.998 003 80.998 003 83.155×10-15f15Enhanced DE3.839×10-042.336×10-033.074×10-045.159×10-04CNDE1.006×10-051.233×10-041.582×10-054.995×10-04f16Enhanced DE-1.031 6-1.031 6-1.031 65.275×10-03CNDE-1.031 6-1.031 6-1.031 64.586×10-16f17Enhanced DE0.3980.3980.3982.413×10-03CNDE0.3980.3980.3985.832×10-16f18Enhanced DE3332.902×10-15CNDE3331.636×10-15f19Enhanced DE-10.153 2-1.268 3-9.902 72.806CNDE-10.153 2-10.153 2-10.153 24.502×10-08f20Enhanced DE-10.402 9-2.375 0-9.875 22.032CNDE-10.402 9-10.402 9-10.402 97.870×10-09f21Enhanced DE-10.536 4-2.146 5-9.575 02.157CNDE-10.536 4-10.536 4-10.536 46.961×10-09 由表4中的数据可知,CNDE算法在大多数测试函数中表现优异。就单峰函数来讲,函数f1、f2和f3精度提高了近一倍,f4和f5也极大地提高了其精度,函数f6可以达到最优值0,噪声函数f7的结果与Enhanced DE算法结果相近。就多峰函数f8-f13来讲,函数精度基本都有提升或至少能够等于Enhanced DE算法结果。就低维函数f14-f21来讲,除函数f15外基本所有函数都能达到最优值,且稳定性较好。 为了更为直观地对比算法的收敛速度,以函数f1为例,绘制出用CNDE算法和Enhanced DE算法所求得的函数收敛图像,如图3所示。 图3 函数收敛图像Fig.3 Convergence curves 另外,将本文算法与其它主流差分进化算法:DE/rand/1/bin、jDE、CODE、Enhanced DE进行对比。DE/rand/1/bin为标准差分进化算法,较其他进化算法原理简单,受控参数少,具有记忆个体最优解和种群内信息共享的特点;jDE为自适应参数差分进化算法,其具有参数自适应的特点,而非根据经验取值;CODE为组合差分进化算法,该方法使用3个试向量生成策略和三个控制参数设置,随机地组合它们来生成试验向量,具有较好的收敛性;Enhanced DE则是最新的在动力学的基础上研究差分进化算法,本文也是在此基础上提出的改进。每个算法对21个测试函数分别独立运行50次,结果均值如表5所示。 表5 与其他主流差分进化算法结果对比Tab.5 Compared with other mainstream differential evolution algorithms 表5中可以看出,CNDE算法相对标准DE算法表现十分优秀,但对比于其他主流差分进化算法却没有十分突出。其实可以考虑将本文所述方法应用到其他主流差分进化算法中。以jDE为例,在保留其原有步骤的基础上,改变变异算子,以本文所述方法构建网络,计算概率,选择目标向量,并执行基于目标函数值排序的选择策略。进而提出基于复杂网络的自适应参数差分进化算法(CN-jDE)。其中参数设计为τ1=τ2=0.1,Fl=0.1,Fu=0.9,其余参数保持不变。在此分别挑选两个单峰,多峰,低维函数进行测试,结果如表6所示。 由表6中数据可以看出,CN-jDE算法在稳定性和求解精度上较jDE算法均表现优异。为更直观地对比算法的收敛速度,以函数为例,绘制出利用算法CN-jDE和算法jDE所求得的函数收敛图像,如图4所示。 表6 jDE与CN-jDE测试结果比较均值(方差)Tab.6 jDE and CN-jDE test results are compared 图4 函数收敛图像Fig.4 Convergence curves 基于网络研究差分进化算法为进化算法的改进提供了新的思路。本文在网络的基础上分析了差分进化算法。该方法将种群中的个体映射成网络中的节点,个体之间的基因信息传播则用网络中的连边表示,这使得基因的传播方向可视化。基因组好的个体以及目标函数值优的个体会有较高的传播概率。虽然对21个标准测试函数的仿真结果表明,对于大部分函数,该方法在收敛速度和计算精度上有一定的提高。但是在测试中,我们发现α的取值对算法的稳定性影响较大,且不同的函数对α的要求也不同。后续需要在α的取值方面做深入的研究。 进一步的研究可尝试将这种方法推广到其它进化算法上。另外对于网络连边上权值的选取可以考虑通过适应度值来确定。除此之外,还可以研究上述所构建出的网络性质如小世界性、无标度性或者不同算法之间所构造的网络的相似性、相关性等。3 算法实现流程

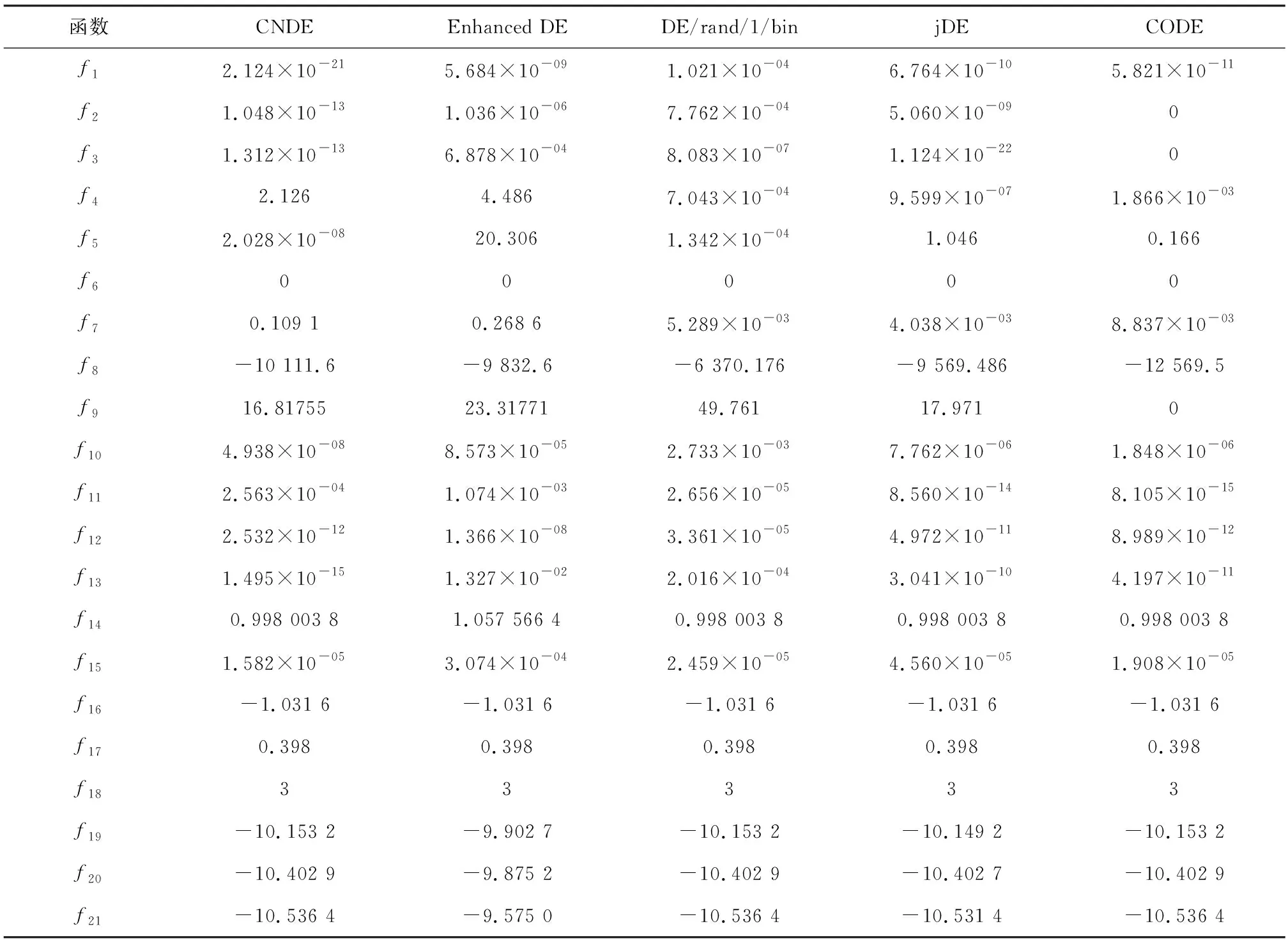
4 实验仿真与分析



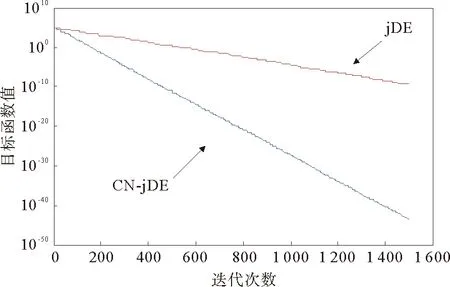
5 结语

