国外工程中抵偿高程面确定方法的研究

喻守刚，李志鹏，余青容，邓庆海

(1.长江空间信息技术工程有限公司(武汉)，湖北 武汉 430011；2.长江航道规划设计研究院，湖北 武汉 430040)

1 引 言

随着国家综合实力和科技水平的提高，越来越多的企业走出国门，承接国外工程项目。然而，国外很多国家，特别是中美洲、非洲等国家地图投影采用的是UTM投影，而我国工程项目多采用高斯投影，这两种投影虽然都属于等角投影方式，但投影后同一地方的长度变形差异还是较大，而考虑到工程施工的需要，测区范围内长度投影变形须按《工程测量规范》要求控制在 2.5 cm/km内，这就需要我们对测区进行投影变形计算分析，选择合适抵偿投影面，从而将测区投影变形的最大值控制在最小[1]。目前，国内对高斯投影抵偿面进行了较多研究和分析，也有单独对UTM投影变形和抵偿分析的研究[2，3]，但很少有将UTM抵偿投影面和高斯抵偿投影面进行关系推导和比较分析的研究。

2 高斯投影与UTM投影

高斯投影是由德国数学家、天文学家、物理学家高斯于19世纪20年代设计，后经德国大地测量学家克吕格补充完善，它是一种横轴等角切椭圆柱投影。见图1(a)，该投影假设某一椭圆柱体横切地球椭球体于某一条经线上，按照等角投影方法将中央经线东、西各3°或1.5°经线范围内的经纬线投影到椭圆柱面上，然后将椭圆柱面展开成平面而成。高斯投影中，中央子午线投影后长度没有变形，其余经线距中央子午线愈远，长度变形愈大且变形比均大于1。我国各种大、中比例尺地形图采用了不同的高斯投影带。其中大于1∶1万的地形图采用3度带；1∶2.5万至 1∶50万的地形图采用6度带。

UTM(Universal Transverse Mercator)全称为通用横轴墨卡托投影，它属于横轴等角割椭圆柱投影，如图1(b)所示，它和高斯投影一样属于正形投影，椭圆柱割地球于南纬80°至北纬84°之间，投影后中央子午线长度比不再是1，而是 0.999 6，两条割线(在赤道上，距离中央子午线约 ±180 km(约±1°40′))投影后没有变形，这样就显著地减少了投影带边缘区域的长度变形，尤其在低纬度地区这种效果更为明显，因此世界上很多低纬度国家和地区都采用UTM投影。UTM平面直角系与高斯投影相同，且两者投影坐标有一个简单的比例关系，因此也是称它为m0=0.999 6的高斯投影[4]。

图1两种投影方式示意图

3 理论基础

3.1 高斯抵偿投影面的建立

如图2所示，AB的长度为S，利用三角形相似等比原理，可以获得测距边基线归算到椭球面改正公式[4]。

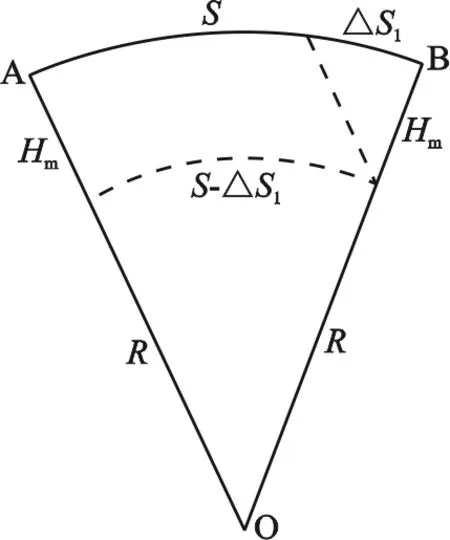
图2 参考椭球面示意图

(1)

式中，Hm为测距边高出参考椭球面的平均高程。

将参考椭球面上某一点(x，y)投影到高斯平面上，可以获得该点的长度比为：

(2)

假设该点上有长度为S的边长，那么该边长投影后的长度为：

(3)

式中：ym为测距边两端点横坐标平均值，△y为测距边两端点横坐标之差，Rm为参考椭球面上测距边中点的平均曲率半径。

将参考椭球面上的大地边长S归算到高斯投影面，边长长度变形为：

将式(1)和式(2)组合，忽略微小项变形后，可以得到测距边投影到高斯平面的总变形为：

(4)

从式(1)和式(2)可以看出△S1为负，△S2恒为正，可以抵消一部分。

由式(4)可知，△S由测距边平均高程Hm、测距边到中央子午线距离ym决定，在实际工程项目中，为保证设计施工前后资料的一致性，通常要求测区中央子午线保持不变，因此ym值基本也不会发生变化，为抵偿测距边的长度变形，只能采取改变投影面高程的方式。

假设测区范围内有一点ya，若选取平均高程面为抵偿投影面，那么△S1就为0。为了使该点投影变形△S完全为0，那么抵偿投影面就应低于平均高程面。此时，假设选取的抵偿投影面为HP，那么可以将式(1)改写为：

(5)

将式(4)代入式(3)中，可以得到投影到抵偿面的变形公式为：

(6)

当△S=0时，可以得到抵偿高程面的计算公式[5]：

(7)

3.2 UTM 抵偿投影面的建立

根据等比投影的性质，UTM投影长度比和高斯投影长度比有如下关系：

mUTM=0.9996m高斯

(8)

由于UTM投影和高斯投影具有相同的投影性质，将式(8)代入到式(3)中，可以得到参考椭球面边长归算到UTM投影面，长度变形为[6]：

(9)

由式(8)和式(9)可知，实测水平距离归算到UTM投影面的长度总变形△S为：

(10)

进行抵偿投影时，△S=0，可以得到UTM抵偿投影面：

(11)

当对同一个测距边既进行高斯投影又进行UTM投影时，测距边的平面高程Hm，距离中央子午线的平面距离ym，坐标差值△y均相同，所以，由式(7)和式(11)可以得到：

HP(UTM)=0.0004R+HP(高斯)

(12)

将地球半径平均值R=6371km代入式(12)中，得到：

HP(UTM)=2548.4+HP(高斯)

(13)

所以，对同一测距边来说，进行抵偿高程面投影时，UTM抵偿投影面比高斯抵偿投影面高 2 548.4 m。

4 抵偿投影面适用范围分析

由于UTM投影坐标系长度变形为0的地方在距离中央子午线 180 km左右，因此UTM投影通常适合较大范围的投影，UTM坐标系在国际坐标系分带中也只有6度分带，而高斯投影中央子午线长度变形为0，投影分带一般有6度分带和3度分带两种，为了准确分析两种抵偿坐标系在投影带不同区域之间抵偿高程面的关系，这里选用6度带进行分析。

在工程测量中，测距边长一般都是几千米，最长也不过十几千米。为方便分析计算，△y取测距边最大坐标差值 15 km，Rm取地球平均半径R，此时抵偿投影面高程式(7)、式(11)可以简化为：

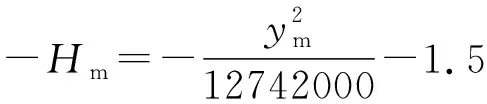
(14)

(15)

在实际工程中，为方便施工放样等测量作业，通常要求设置抵偿高程面不能与测区平均高程相差太大，这里将ABS(HP-Hm)≤200 m内，可以得到高斯投影抵偿高程面的范围为-50.7 km≤ym(高斯)≤50.7 km，UTM投影抵偿高程面的范围为 -187.1 km≤ym(UTM)≤-172.9 km和172.9 km≤ym(UTM)≤187.1 km。

图3 6度带范围内抵偿高程面与Y轴距离关系

从图3中可以看出，UTM抵偿投影面的适用范围分为两部分，并且这两部分分别和距离中央子午线为 ±180 km的经线呈对称分布，每部分适用范围只有 14.2 km，而高斯投影适用范围和中央子午线呈对称分布，两部分完全相连一起，总范围为 101.4 km。UTM抵偿高程投影只能适合距离中央子午线为 180 km的小范围工程项目，而距离中央子午线较近的大范围工程项目选择高斯抵偿投影较为合适[7，8]。

5 工程实例

Zenzo水电站位于安哥拉境内北宽扎省和南宽扎省交界处的宽扎(Cuanza)河上，是宽扎河中段规划的7个梯级电站中的第4级，大坝设计装机容量为 950 MW，最大坝高 115 m，坝轴线长度 1 000 m，坝顶高程 421 m，为安哥拉国内最大水电站之一。Zenzo水电站测区范围为东经14°44′～14°49′，南纬9°41′～9°46′，为长宽各约 8 km～9 km的多边形区域。为满足设计和施工的精度要求(2.5 cm/km)，需要在测区范围内建立抵偿坐标系减少投影变形，同时为保证和前期勘测设计资料的一致性，抵偿坐标系的中央子午线须保持东经15°不变。如图4所示，在测区内建有D级GPS网，最大边长约 8.5 km，测区内平均高程为 346 m。

图4 测区控制网布置图

(1)方案一高斯投影

由式(4)可以计算出，当采用全站仪进行施工测量放样时，测距边抵偿前的投影变形量最大为：

该长度变形明显不满足边长变形小于 2.5 cm/km的要求，因此需要选择抵偿高程面进行抵偿投影，按照投影变形最大值为零的原则进行抵偿投影，由公式(7)可以得到抵偿高程面为：

HP(高斯)=346-41=305 m

要满足长度变形小于2.5 cm/km时，抵偿高程面需满足145.7 m

(2)方案二UTM投影

HP(UTM)=2548.4+305=2853.4 m

要满足长度变形小于2.5 cm/km时，抵偿高程面需满足2 694.1 m

从该水利工程不同投影方式下抵偿高程面的计算可以看出，选用UTM投影时，抵偿高程面为 2 853.4 m与测区的平均高程 346 m差距较大，而选用高斯投影时抵偿投影面为 305 m，与测区平面高程较为相近。综上考虑，在不限制投影方式时，该工程选择高斯投影建立抵偿坐标系较为合适。

6 结 语

高斯投影和UTM投影是两种常见的不同投影，当采用两种不同投影方式建立抵偿坐标系时，由于中央子午线比例因子的差异，抵偿高程面存在明显差异，本文通过理论推导得出UTM抵偿投影面比高斯抵偿投影面高 2 548.4 m。由于这个差异，在建立抵偿投影面时，两者的适用范围完全不同，当测区距离中央子午线距离在 ±50.7 km以内时，选用高斯投影建立的抵偿高程面与测区平均高程在 200 m内，当测区距离中央子午线为 -187.1 km～-172.9 km和172.9 km～187.1 km时，选用UTM投影方式较为合适。本文中抵偿高程面建立方法不仅可以应用于水利工程，还可以拓展到其他小范围的工程项目。