基于改进OK模型的土壤有机质空间分布预测*——以宜都市红花套镇为例

段丽君, 郭 龙, 张海涛, 琚清兰



基于改进OK模型的土壤有机质空间分布预测*——以宜都市红花套镇为例

段丽君, 郭 龙, 张海涛**, 琚清兰

(华中农业大学资源与环境学院 武汉 430070)

选择合适的土壤有机质(SOM)预测模型是提高区域化空间分布模拟精度的前提, 也是监测土壤碳库动态变化和指导农田土壤肥力投入的基础。以湖北宜都红花套镇柑橘区为例, 设置普通克里格(OK)插值的SOM结果作对照, 分别建立SOM及其最显著相关辅助变量碱解氮间的建模协同克里格(COK1)、全局协同克里格(COK2)和两个融合辅助变量协同相关性的改进OK模型(CCOK1、CCOK2), 探讨纳入辅助变量、改变辅助信息插值数量以及结合辅助变量协同相关性对SOM含量预测的影响。结果表明: 1)OK、CCOK1和CCOK2的块基比为25%~75%, 表现出中等空间自相关性, 而COK1和COK2的块基比小于25%, 具有强烈的空间自相关, SOM的空间异质性受结构性因素影响的比重更大。2)SOM的预测含量范围为7.38~29.03 g×kg-1, 使用COK1和COK2模型插值获得的有机质空间分布较OK更为破碎, CCOK1和CCOK2的插值结果则呈连续片状分布, 更符合研究区土地利用类型分布的实际情况。3)SOM的空间分布预测精度由高到低依次为CCOK1≈CCOK2>COK2>COK1≈OK, OK和COK1两者精度指标相近, COK2的拟合效果有一定改进, 但CCOK1和CCOK2的相关系数()分别从0.10升高到0.70和0.69, 均方根误差(RMSE)分别降低了15.40%和14.78%, 预测精度最高。因此, 本研究提出的融合辅助变量协同相关性的改进OK模型的估算效果最优且在最大程度上提高辅助信息的参与度, 可为SOM预测提供参考。

土壤有机质; 辅助变量; 碱解氮; 协同相关性; 改进OK模型; 空间自相关性

土壤有机质(soil organic matter, SOM)属土壤重要组成部分[1], 是植物必需营养元素的主要来源[2], 虽然在土壤总重量中所占比重不大, 但其含量是衡量土壤肥力水平的一项重要指标[3-5]。柑橘(Blanco.)产业是湖北省重要经济支柱之一, 种植面积达全省果园总面积的45%, 然而近年来由于柑橘园SOM含量总体偏低[6], 严重抑制橘树的生长发育, 导致柑橘产量及品质均有降低[7]。因此, 为科学指导柑橘园精准施肥, 需要建立快速准确的方法预测SOM空间分布与含量。

受多种成土因素和生态过程影响, 即便是小区域尺度内的SOM含量也呈现出不同程度的空间异质性和非平稳性[8-11], 单纯通过野外土壤田间调查又难以满足精确获取SOM空间分布信息的实际需求。为解决以上问题, 近年来诸多学者将预测SOM含量的关注点放在能够对未采样区域待估点进行无偏最优估计[12]的克里格法(Kriging)上。在普通克里格插值法(Ordinary Kriging, OK)的应用方面, Singh等[13]提出在不同果树种植园中, 通过OK对SOM进行空间估计的不确定性比非空间方法低且能在未采样位置获得满意的预测结果; 李增兵等[14]使用不同插值方法分别对历城区不同地貌类型建模, 得到OK法更适用于平原区的结果。OK方法虽能考虑SOM的空间自相关性和异质性[15], 但仅依赖土壤样本建模集有机质数据插值, 并不能发挥辅助变量对估算SOM的优势。协同克里格插值法(Cokriging, COK)则可基于不同样点支撑[16-17], 借助同一时空不同变量的协同区域化特征, 用样品多的辅助变量对样品少的目标变量SOM进行估值[18]。苏晓燕等[19]和Yang等[20]提出, 辅助变量的个数大于目标变量且辅助变量与目标变量的相关性越强时, 使用COK越能提高预测精度。但COK的建模精度受辅助变量插值样点数量影响很大, 且交叉变异函数能否充分考虑目标变量和辅助变量间的相关信息以及是否可在空间分布模拟中维持单变量的结构性等问题尚需进一步补充与验证。因此, 本文结合以上2种传统克里格插值法的特点, 提出建立融合辅助变量协同相关性的改进OK模型(improved OK models with cooperative correlation of auxiliary variables, CCOK)。该模型在保持目标变量与辅助变量样点支撑一致且数目有限的情况下融入COK法中的协同区域化思想, 假设目标变量及其辅助变量受到同样的区域化现象或空间过程影响, 各变量不但存在自相关性, 而且与其他变量之间存在交互相关性, 尝试将传统OK法插值数据从单一变量发展到两个相关性极显著的变量函数, 既兼顾了目标变量及其辅助变量的空间结构相似性[21], 又可借助辅助变量提高目标变量实测值与预测值的拟合精度。

本研究以湖南省宜都市红花套镇为研究区, 基于协同区域化理论, 先后利用建模集辅助变量、全局辅助变量对该地SOM建立COK模型(COK1、COK2), 探索性构造CCOK模型(CCOK1、CCOK2), 并将插值结果与OK模型作对比, 分别通过探讨纳入辅助变量、改变辅助变量插值数量以及结合辅助变量协同相关性对SOM含量预测的影响, 获得可显著提高SOM拟合精度的空间插值方法, 以期为监测土壤农田肥力投入情况及增加农业经济效益提供参考。

1 材料与方法

1.1 研究区概况

湖北省宜都市红花套镇处于鄂西山区向江汉平原过渡的地带(30°26′45″~30°35′59″N, 111°14′13″~ 111°26′38″E), 总面积为149 km2。境内西北地势高, 以丘陵山地为主; 东南地势低, 以冲积平原为主, 土地肥沃。该镇属亚热带湿润季风气候, 年均气温16.8 ℃, 年均降雨量1 200 mm, 全年无霜期275 d, 水文、生物、矿产资源丰富, 生态良好, 适宜水稻(L.)、棉花(.)和柑橘生长。其中柑橘种植面积28 km2, 年产量达10万余t, 素有“万亩桔乡”的美称。本研究区内高程范围为42~112 m, 园地、林地、耕地和其他土地利用类型分别占总面积的72.46%、0.59%、0.13%和26.82%(图1)。主要土壤类型为黄棕壤、水稻土, 也有少量潮土、紫色土和石灰土。

图1 研究区地理位置、土地利用概况及土壤样点分布

1.2 数据来源与预处理

在已有红花套镇1∶10 000比例尺地形图、第2次土壤普查相关资料的基础上, 综合地形地貌、土地利用类型、土壤类型以及植被覆盖等相关因素预先设置研究区范围。当该地区柑橘收获且未施用肥料之时, 进行实地调查并结合实际因素对样点位置做适当调整。使用差分式全球定位系统(DGPS)记录经纬度及高程, 采集样点处0~20 cm表层土。采样在平原的园地、耕地区样点内以梅花形法进行, 在丘陵的林地区样点内以蛇形法进行, 共获得329个土壤样本。

地形平缓的小区域内SOM含量分布主要受其他土壤属性影响[20], 因此根据研究区主要土壤养分的分布情况、主要耕种作物的土壤环境营养元素需求特性以及当地农业生产等方面的实际情况, 获取表1中土壤属性数据作为影响因子参与研究, 获取方法均参考文献[22]。

使用SPSS 19.0中3倍标准差法检测样本数据中并无需要剔除的异常值, 再通过ArcGIS 10.2中子要素集功能对样点数据集进行均匀随机划分, 最终获得建模集数据263个(80%), 验证集数据66个(20%)。

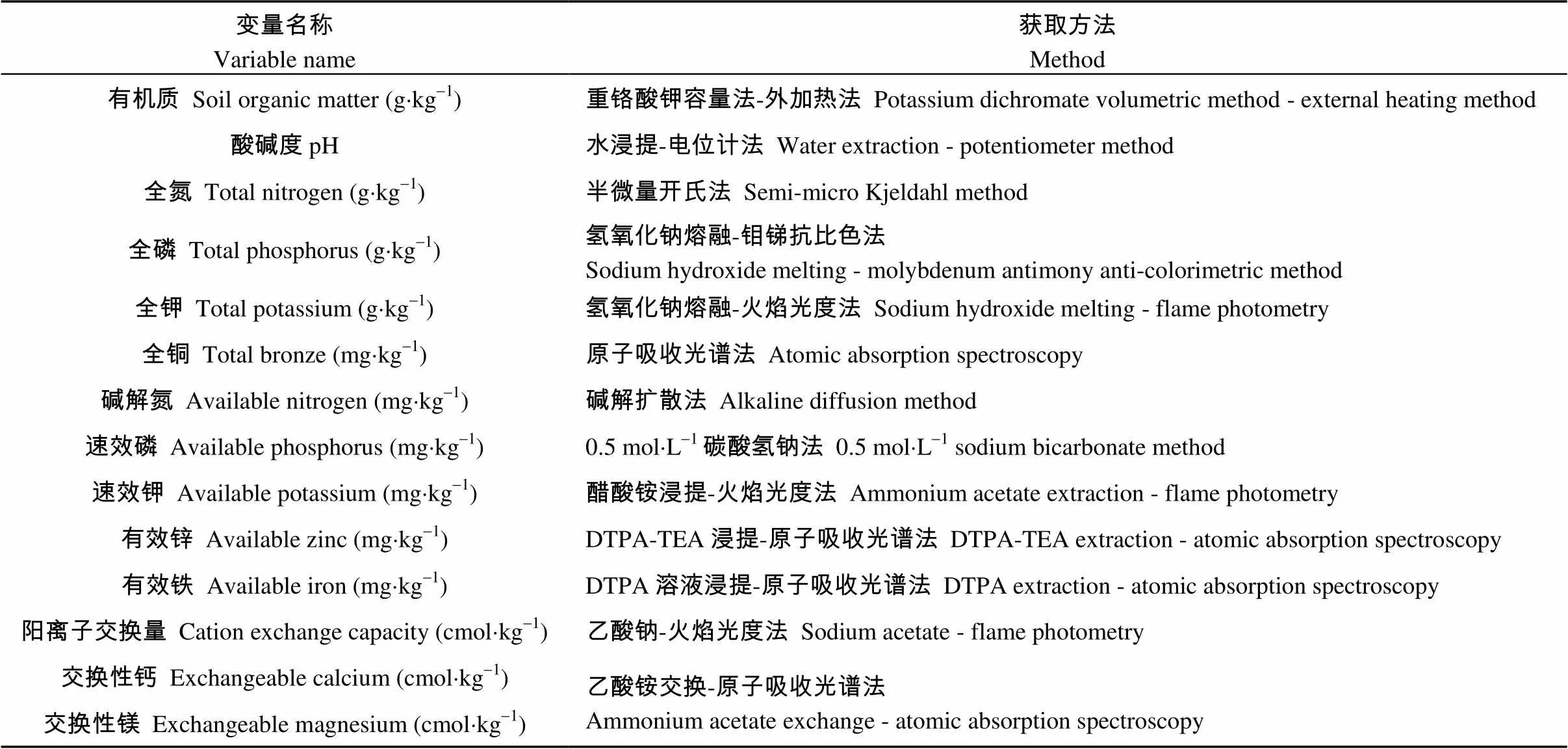
表1 研究区样点土壤属性数据获取内容及方法

1.3 研究方法

1.3.1 空间自相关分析

空间自相关分析是用来反映空间邻近区域某变量属性值的相似程度和空间分布的聚集特征, 全局Moran’s是其中最常用的检验统计量[23-25]。

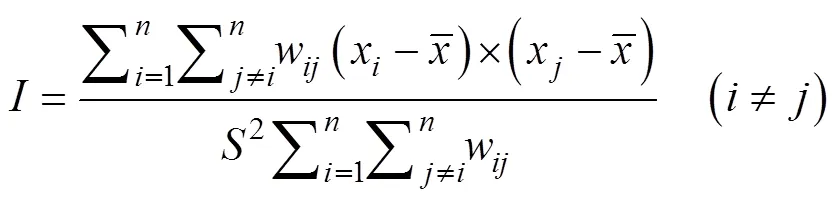
1.3.2 OK模型

OK是单个变量的局部线性最优无偏估计方法, 也是Kriging中最基础的方法之一。它能够根据给定区域内相邻实测点的加权平均值, 为变量在未测量位置提供预测值。该方法通过考虑实测点表示的固有随机函数来简要描述[26]。

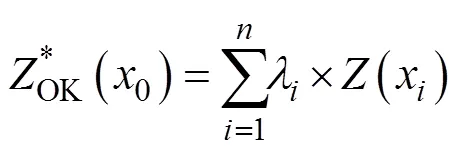
1.3.3 建模COK模型与全局COK模型

在统计意义及空间位置上均具有某种程度相关性, 并且定义于同一空间域中的区域化变量, 即具有协同区域化特征[16]。一般情况下, 结合了辅助变量信息的协同克里格能够比普通克里格进行更多的预测。本文提出的建模COK模型与全局COK模型, 其目标变量均为建模集SOM数据, 区别在于建模COK模型选取了建模集中辅助变量参与插值, 而全局COK模型则选取了全局数据的辅助变量参与插值, 以此比较改变辅助变量插值数量对SOM预测精度的影响。

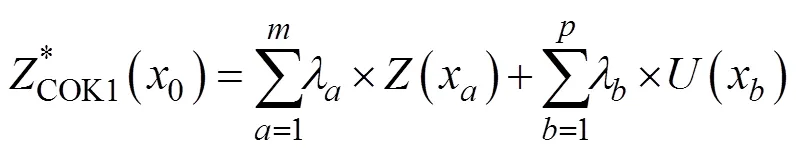
1.3.4 CCOK模型

CCOK模型是传统OK插值方法与COK插值原理相结合的改进模型, 它考虑了协同相关性引入辅助变量, 是对代数量化后的主变量与辅助变量进行OK插值的方法。为充分说明与主变量存在极显著相关的辅助变量对提高插值精度具有重要意义, 同时验证对不同单位的变量不设置数据标准化预处理也不会影响最终预测效果, 特列以下公式完成CCOK建模。

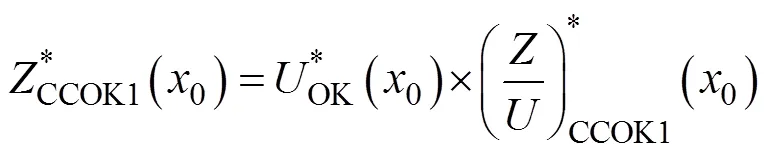
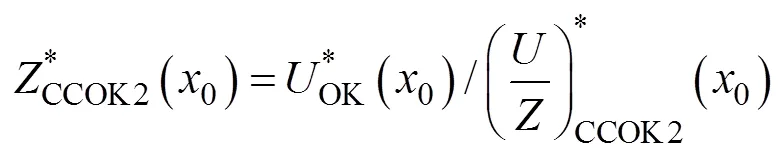
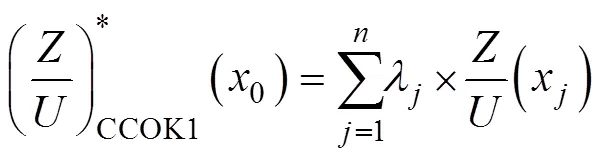
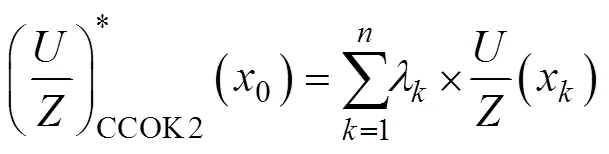
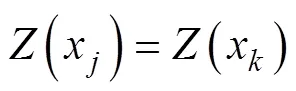
1.4 预测模型精度验证

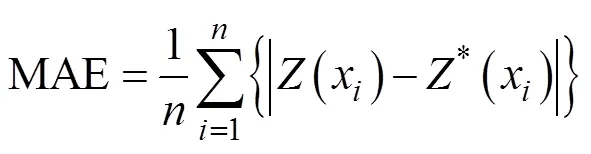
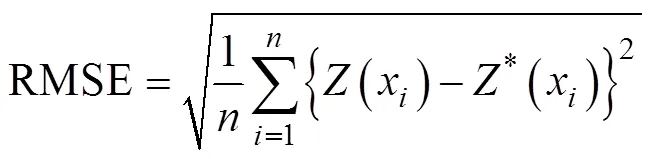
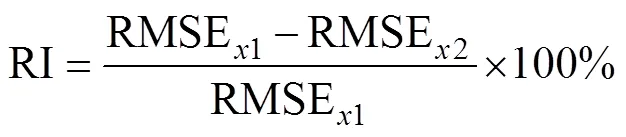
式中:代表样本数,(x)代表样本的实测值,(x)代表样本的预测值, RMSE1代表使用OK插值得到的RMSE值, RMSE2代表使用COK或CCOK插值得到的RMSE值。由于离差被绝对值化, 不会出现正负相抵消的情况, 因而平均绝对误差MAE能更好地反映预测值误差的实际情况; 均方根误差RMSE是插值精度的量度, 其值越小则说明插值方法越精确; 相对精度改进值RI为正值代表COK或CCOK方法较OK方法的预测精度更高, 值越大说明提高越多, RI为负值则表示COK或CCOK方法预测精度低于OK方法。

1.5 软件平台

利用SPSS 19.0完成原始数据非空间分析(剔除异常值、基本特征统计和最相关辅助变量选取), 通过GeoDa证明变量间存在的区域协同化特征(全局空间相关性分析), 采用ArcGIS 10.2进行空间分析(栅格计算)、地统计学分析(随机划分数据集、构建最优半方差模型、完成OK、COK与CCOK插值)。

2 结果与分析

2.1 研究区样点SOM含量数据的特征统计

表2中全部数据集的SOM含量均值为16.97 g×kg-1, 范围在6.07~29.18 g×kg-1, 最大值和最小值间差异显著且变异系数为24.87%, 均属中等变异, 说明SOM在该研究区范围内具有一定变异性, 适合空间局部估计。建模集中的有机质数据(偏度=0.07, 峰度=-0.08)通过K-S(Kolmogorov-Smirnov Z)检验, 符合正态分布, 可直接用于插值建模。

2.2 研究区样点SOM最相关辅助变量的选取

表3显示了该研究区中与SOM相关性由高到低依次排序的前7种影响因子及其Pearson相关系数。有机质与碱解氮、有效铁、全氮和全磷表现为正相关, 与交换性镁、阳离子交换量和速效钾表现为负相关。

表2 研究区土壤有机质含量的基本统计特征

其中, SOM与碱解氮间的相关系数为0.815, 呈极显著正相关, 相关系数高于其他因子。这是因为SOM主要由C、H、O、N等元素构成, 碱解氮中则包含无机的矿物态氮和部分有机质中易分解的、比较简单的有机态氮[27], 氮素是二者重要组成成分中的共同元素。在受同一区域下水热条件、成土特征及微生物反复作用下,SOM与碱解氮之间的耦合关系逐渐趋于动态平衡[28],理论上有机质含量丰富, 熟化程度高, 碱解氮的含量就高, 反之则含量降低。但实际上, 碱解氮作为一种速效养分, 其含量及空间分布还与人为投入氮素化肥数量等外界因素有一定关联[29], 可以说碱解氮中的氮素主要来源于有机质, 但其含量、组成、形态和有效性又不完全等同于有机质。此外, 相关研究表明协同变量与自变量间的相关系数大于0.5时更能在预测结果中体现协同区域化优势[30], SOM与碱解氮间的相关性符合该条件并远高于其他因子。因此, 研究选择碱解氮作为预测SOM的最相关辅助变量。

表3 研究区土壤有机质与影响因子的相关性

**和*分别表示在0.01和0.05水平(双侧)上显著。** and * indicate significant correlation at 0.01 and 0.05 levels (bilateral), respectively.

2.3 研究区样点SOM、碱解氮的空间自相关与交互相关分析

SOM、碱解氮的Moran’s指数分别为0.11、0.08, 具有一定正空间自相关性, 当对两者建立简单函数关系后指数值分别提高到0.19和0.15(表4)。同时, 综合比较代表标准差的得分与代表概率的值发现, 属性的空间聚类置信度也从95%升为99%, 说明SOM与碱解氮在空间分布上表现出良好的交互相关性, 促进了其函数关系呈现出极显著的空间自相关性(<0.01), 这是将碱解氮作为辅助变量建立预测SOM的CCOK模型的关键依据。

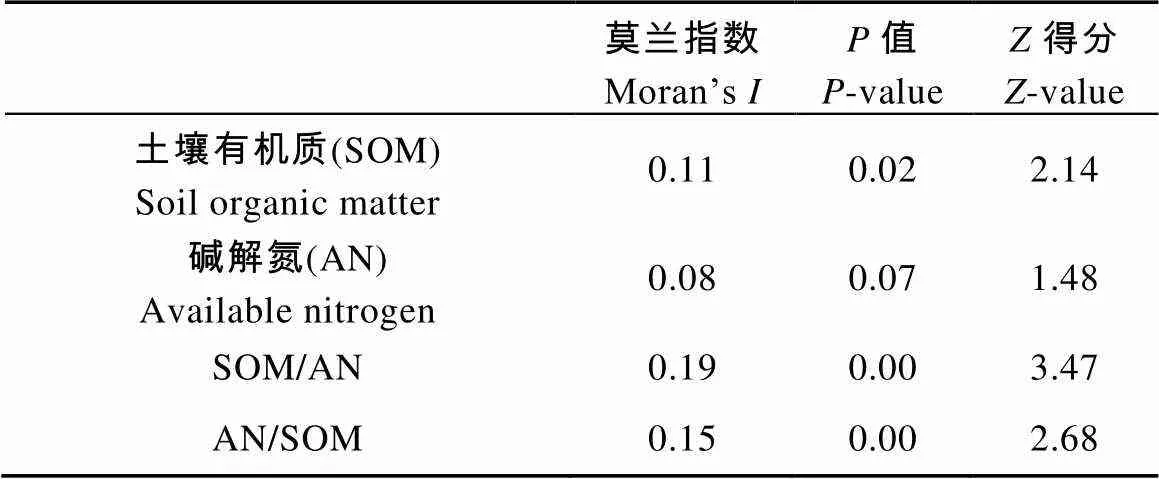
表4 研究区土壤有机质、碱解氮空间自相关与交互相关分析

2.4 不同克里格插值模型对研究区SOM半方差模型的选择与分析

表5为使用不同克里格模型对SOM预测时选择的最优半方差模型及其显示参数。半方差函数预测误差的作用是为Kriging插值判断拟合的最优模型。遵循平均值越趋近于零越无偏、均方根误差RMSE越小越精准的原则, OK、COK1、COK2、CCOK1和CCOK2分别选择高斯模型、球状模型、指数模型、指数模型和指数模型作为插值的半方差模型。模型参数中, OK和COK2的块金值较大, 说明存在由于采样或分析引起的各种正基底效应[31]; CCOK1的变程为3 627.41 m, 是由于为符合OK插值数据需正态分布的条件, 对有机质/碱解氮数据进行了对数转换, 转换后的数值为-2.15~-0.71, 极差仅为1.44, 因此在研究区的大面积连续范围内均表现出空间分布的相近性。而其他方法的变程较小, 表示SOM含量在短距离内具有空间连续性[32]。就基台效应而言, COK1、COK2具有强烈的空间相关性, OK、CCOK1、CCOK2表现出中等空间相关性, 说明SOM的空间异质性受结构性因素影响的比重更大。图2是对应于表5的SOM半方差函数图。分析图像中绘制曲线通过表示半变异函数平滑变化的平均化数据情况, 可更加直观地反映各插值模型的拟合效果。其中, CCOK1的半方差函数拟合效果相较于其他方法表现微弱甚至难以体现, 但因其变程范围远大于步长距离, 变程内的区域化变量仍存在空间相关状态。所以, 需将SOM半方差模型参数及函数图综合分析, 才能完成使用不同方法对SOM预测的合理预判。

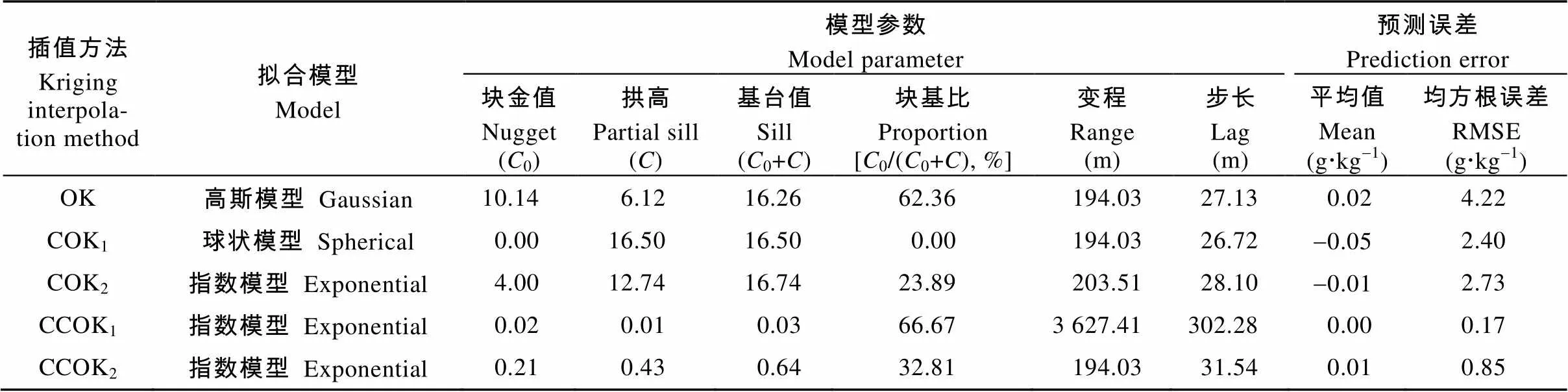
表5 研究区不同克里格插值模型的土壤有机质半方差模型参数

OK为普通克里格; COK1和COK2分别为协同克里格和全局协同克里格; CCOK1和CCOK2为两个融合辅助变量协同相关性的改进OK。OK: ordinary Kriging; COK1and COK2are modeling Cokriging and global Cokriging; CCOK1and CCOK2are two improved OK models with cooperative correlation of auxiliary variables.

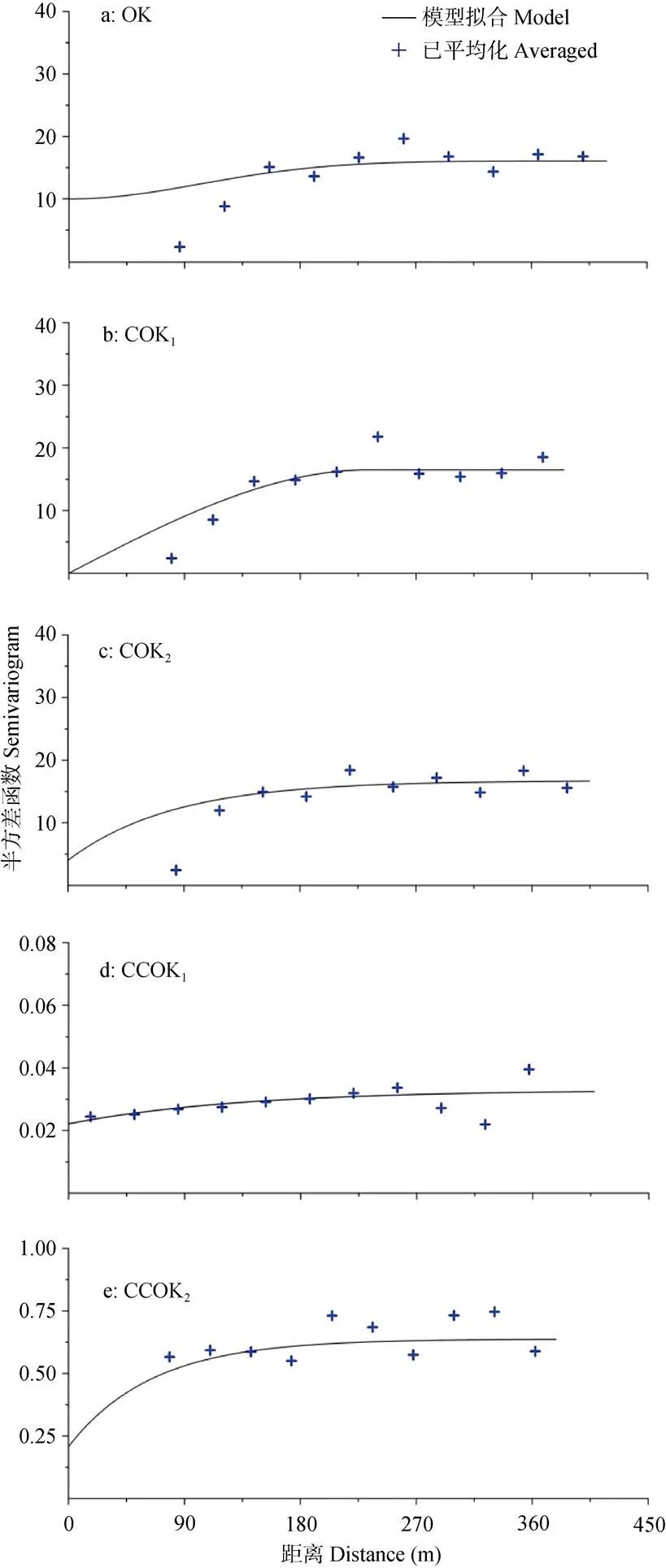
图2 研究区不同克里格插值模型的土壤有机质半方差函数图

OK为普通克里格; COK1和COK2分别为协同克里格和全局协同克里格; CCOK1和CCOK2为两个融合辅助变量协同相关性的改进OK。OK: ordinary Kriging; COK1and COK2are modeling Cokriging and global Cokriging; CCOK1and CCOK2are two improved OK models with cooperative correlation of auxiliary variables.

2.5 不同克里格插值模型对研究区SOM空间分布预测的差异比较

对比图3研究区的SOM空间分布预测图可知, 使用5种模型取得的预测结果分布情况整体相似, SOM含量范围为7.38~29.03 g×kg-1。按照<5 g×kg-1为极低、5~10 g×kg-1为低、10~15 g×kg-1为偏低、15~30 g×kg-1为适宜、>30 g×kg-1为丰富的标准[33]划分, 研究区大部有机质含量适宜, 小面积区域含量低, 无含量极低或丰富地区, 呈现出“西北和东南高, 中部高低错落”的分布趋势, 这与该研究区的土地利用类型分布格局有关。西北部为与小面积林地衔接的柑橘种植带, 受人为干扰少, 凋落物富集, SOM分解速度慢便于长期积累。东南部则为柑橘的集中种植区, 为促进果树生长和发育、提高果树产量及品质, 定期的人为施肥和排水增加了SOM含量[34]。而研究区中部的柑橘园地与零星耕地、其他土地利用类型交叉分布, 并以土壤为媒介发生长期物质交换, 产生相互作用, 导致了有机质含量分布不均且高低差异显著, 因此是柑橘园中调控施肥用量的重点位置。

以OK预测结果为对照, 添加了碱解氮作辅助变量的COK1、COK2模型插值获得的有机质分布更加破碎, 空间镶嵌结构更为复杂[35], 一部分原因是OK模型本身具有平滑效应使得空间预测表现连续, 另一部分原因是COK1、COK2模型通过目标信息及其辅助信息间建立的交叉变异函数促使生成更加详尽的空间信息表达, 且COK2较COK1的辅助变量样点分布更密, 因此能够观察到有机质含量的明显变化, 并体现出局部变异细节。

与建立前3种模型得到的SOM预测图呈点状放射相比, CCOK1、CCOK2模型的插值结果为连续片状放射。这是由于OK、COK1和COK2模型以建模集有机质为惟一或主要数据源, 在数字制图中继续维持SOM的空间结构特征。而CCOK1、CCOK2方法的建模数据源选择为有机质与碱解氮之间的代数量化数据, 虽然经公式转回为对SOM的预测, 但同时使用样点支撑一致的变量参与插值, 使得预测制图能够充分体现出辅助变量对目标变量的协同相关性, 有机质含量高者更高、低者更低, 既突出了差异信息, 也更符合研究区土地利用类型分布的实际情况。

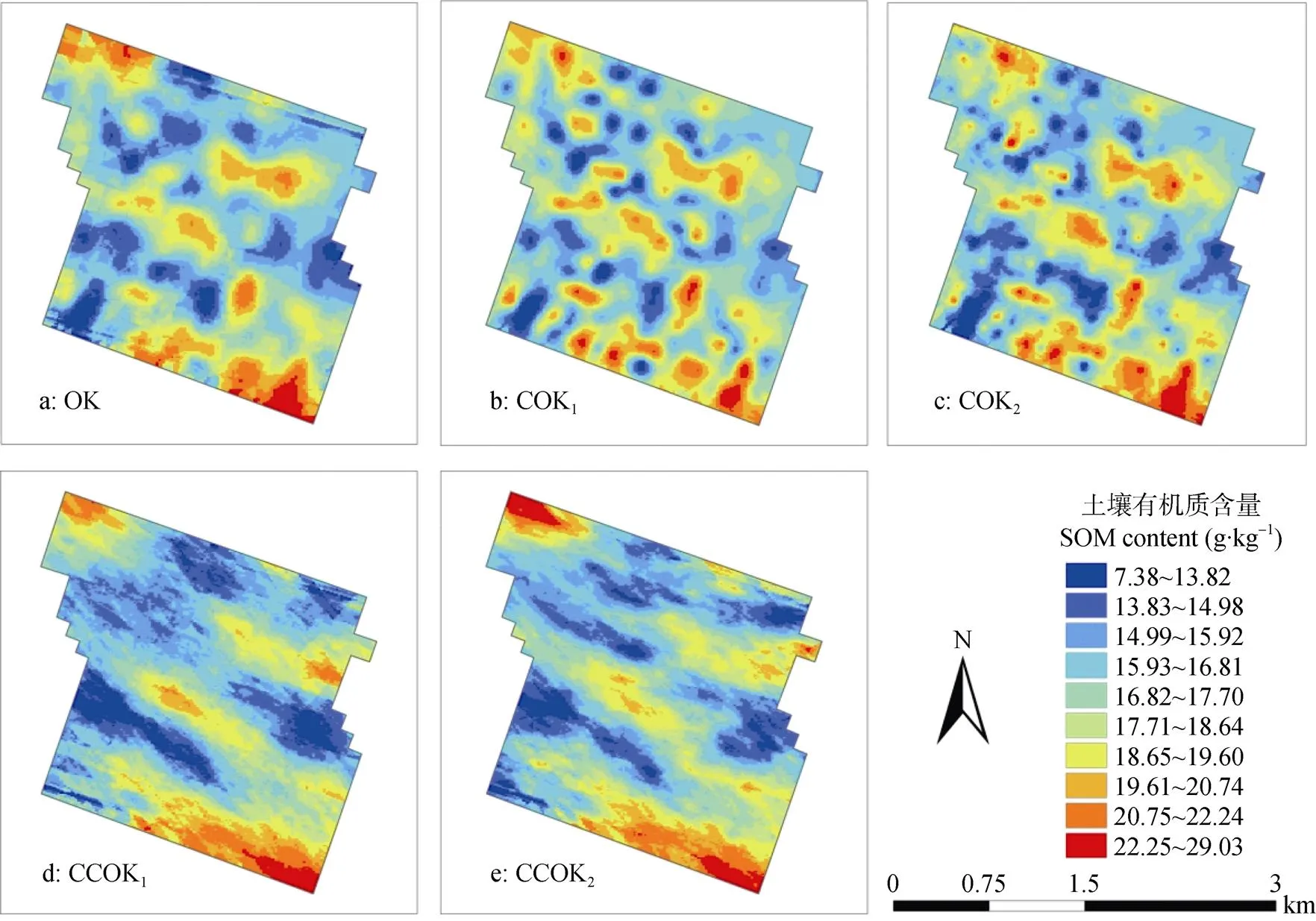
图3 不同克里格插值模型对研究区土壤有机质空间分布预测的异同

OK为普通克里格; COK1和COK2分别为协同克里格和全局协同克里格; CCOK1和CCOK2为两个融合辅助变量协同相关性的改进OK。OK: ordinary Kriging; COK1and COK2are modeling Cokriging and global Cokriging; CCOK1and CCOK2are two improved OK models with cooperative correlation of auxiliary variables.

2.6 不同克里格插值模型对研究区SOM含量预测的精度验证

其中, OK和COK1两者间各精度指标相近, 充分证明当作为目标变量的SOM与作为辅助变量的土壤碱解氮样点支撑完全相同时, COK方差即为OK方差[16], 是否添加辅助变量对预测目标变量无较大意义。COK2则是在已有COK1模型的基础上, 将建模集辅助变量改为全局数据集辅助变量参与插值,通过增大样点数量提升了辅助预测效果。CCOK1和CCOK2的建模原理相同, 都在兼顾目标变量及其辅助变量空间结构相似性的同时, 最大程度地发挥了辅助变量的协同相关作用, 由二者并无较大差异的插值结果也能间接证明CCOK模型对未经标准化处理的建模数据仍然适用。综合、MAE、趋势线与1∶1参考线拟合程度、RMSE、RI这5项指标分析, SOM空间分布预测精度由高到低依次为CCOK1≈CCOK2> COK2>COK1≈OK, CCOK模型在很大程度上提升了SOM含量的拟合效果。本文提出的建立融合辅助变量协同相关性的改进OK模型进行SOM空间分布预测可缩小实测值与预测值间差距, 为研究区柑橘种植提供精准施肥建议。

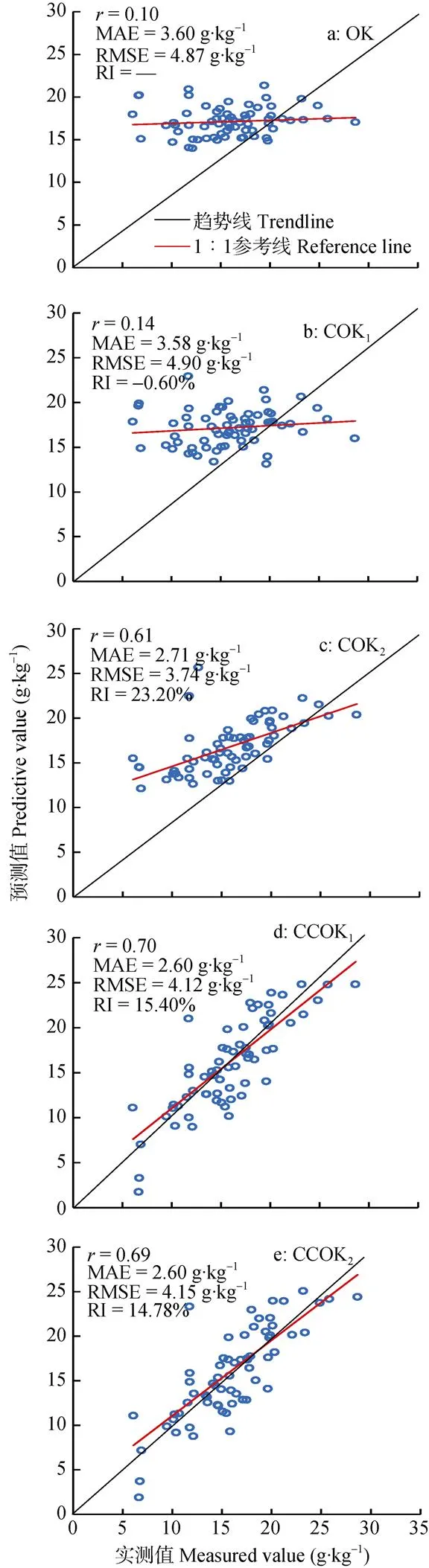
图4 不同克里格插值模型对研究区土壤有机质预测的精度指标对比

OK为普通克里格; COK1和COK2分别为协同克里格和全局协同克里格; CCOK1和CCOK2为两个融合辅助变量协同相关性的改进OK。OK: ordinary Kriging; COK1and COK2are modeling Cokriging and global Cokriging; CCOK1and CCOK2are two improved OK models with cooperative correlation of auxiliary variables.

3 结论

1)本柑橘种植区中, 使用几种克里格插值模型预测得到的SOM含量均为7.38~29.03 g×kg-1, 整体呈现 “西北和东南高, 中部高低错落”的分布趋势。

2)以OK模型作对照, 与辅助变量间建立交叉变异函数的SOM的空间变异性更容易被半方差模型识别, 使得COK1、COK2因模型参数存在强烈空间自相关在SOM空间分布上表现破碎,并能维持单变量空间结构性。然而,通过改变辅助信息样点数量提高SOM预测精度, 既会增加研究成本又未充分考虑每个样点上目标变量与辅助变量间的交互关系, 可能引进更多变异, 因此使用该模型存在一定局限。

3)CCOK1和CCOK2模型则能在目标变量与辅助变量样点支撑一致且样点数目有限的情况下, 最大程度发挥辅助变量的协同相关性, 其优势不仅体现在SOM的空间分布模拟结果最符合该研究区土地利用类型的实际分布情况, 更表现在CCOK1和CCOK2的模型预测精度分别提高了15.40%、14.78%, 且相关系数从0.10显著升到0.70、0.69。

4)此研究已证明,使用融合辅助变量协同相关性的改进OK模型可实现对研究区SOM的精准预测,能够为区域柑橘种植区施肥提供合理建议,而其适用范围及条件将是下一步讨论的重点。

[1] WANG K, ZHANG C R, LI W D. Comparison of geographically weighted regression and regression kriging for estimating the spatial distribution of soil organic matter[J]. GIScience & Remote Sensing, 2012, 49(6): 915–932

[2] WALLACE A. Soil organic matter is essential to solving soil and environmental problems[J]. Communications in Soil Science and Plant Analysis, 2008, 25(1/2): 15–28

[3] 黄昌勇, 徐建明. 土壤学[M]. 第3版. 北京: 中国农业出版社, 2010: 29–30 HUANG C Y, XU J M. Soil Science[M]. 3rd ed. Beijing: China Agriculture Press, 2010: 29–30

[4] 马泉来, 高凤杰, 张志民, 等. 我国东北黑土丘陵区小流域土壤有机质空间分布模拟[J]. 环境科学研究, 2016, 29(3): 382–390 MA Q L, GAO F J, ZHANG Z M, et al. Simulation of spatial distribution of soil organic matter in a mollisol watershed in Northeastern China[J]. Research of Environmental Sciences, 2016, 29(3): 382–390

[5] WANG K, ZHANG C R, LI W D, et al. Mapping soil organic matter with limited sample data using geographically weighted regression[J]. Journal of Spatial Science, 2014, 59(1): 91–106

[6] 鲁剑巍, 陈防, 王富华, 等. 湖北省柑橘园土壤养分分级研究[J]. 植物营养与肥料学报, 2002, 8(4): 390–394LU J W, CHEN F, WANG F H, et al. Study of classification of the soil nutrient status of citrus orchard in Hubei Province[J]. Plant Nutrition and Fertilizer Science, 2002, 8(4): 390–394

[7] 叶荣生. 有机肥对柑橘营养及生长的影响[D]. 重庆: 西南大学, 2013: 16–18YE R S. Effect of organic fertilizer on nutrition and growth of citrus[D]. Chongqing: Southwest University, 2013: 16–18

[8] SCULL P, FRANKLIN J, CHADWICK O A, et al. Predictive soil mapping: A review[J]. Progress in Physical Geography: Earth and Environment, 2003, 27(2): 171–197

[9] LI Y. Can the spatial prediction of soil organic matter contents at various sampling scales be improved by using regression kriging with auxiliary information?[J]. Geoderma, 2010, 159(1/2): 63–75

[10] LI S C, ZHAO Z Q, XIE M M, et alInvestigating spatial non-stationary and scale-dependent relationships between urban surface temperature and environmental factors using geographically weighted regression[J]. Environmental Modelling & Software, 2010, 25(12): 1789–1800

[11] GUO L, ZHAO C, ZHANG H T, et al. Comparisons of spatial and non-spatial models for predicting soil carbon content based on visible and near-infrared spectral technology[J]. Geoderma, 2017, 285: 280–292

[12] XIAO Y, GU X M, YIN S Y, et al. Geostatistical interpolation model selection based on ArcGIS and spatio-temporal variability analysis of groundwater level in piedmont plains, Northwest China[J]. Springerplus, 2016, 5(1): 425

[13] SINGH A, SANTRA P, KUMAR M, et al. Spatial assessment of soil organic carbon and physicochemical properties in a horticultural orchard at arid zone of India using geostatistical approaches[J]. Environmental Monitoring and Assessment, 2016, 188(9): 529

[14] 李增兵, 赵庚星, 赵倩倩, 等. 县域耕地地力评价中土壤养分空间插值方法的比较研究[J]. 中国农学通报, 2012, 28(20): 230–236LI Z B, ZHAO G X, ZHAO Q Q, et al. Comparison of spatial interpolation methods for soil nutrients in cultivated land fertility evaluation[J]. Chinese Agricultural Science Bulletin, 2012, 28(20): 230–236

[15] LIU Y L, GUO L, JIANG Q H, et al. Comparing geospatial techniques to predict SOC stocks[J]. Soil and Tillage Research, 2015, 148: 46–58

[16] 刘爱利, 王培法, 丁园圆. 地统计学概论[M]. 北京: 科学出版社, 2012: 154–155 LIU A L, WANG P F, DING Y Y. Introduction to Geostatistics[M]. Beijing: Science Press, 2012: 154–155

[17] 侯景儒, 黄竞先. 地质统计学的理论与方法[M]. 北京: 地质出版社, 1990: 59–60 HOU J R, HUANG J X. Theory and Methods of Geostatistical[M]. Beijing: Geological Publishing House, 1990: 59–60

[18] 史舟, 李艳. 地统计学在土壤学中的应用[M]. 北京: 中国农业出版社, 2006: 85–86SHI Z, LI Y. Geostatistics and its Application in Soil Science[M]. Beijing: China Agriculture Press, 2006: 85–86

[19] 苏晓燕, 赵永存, 杨浩, 等. 不同采样点数量下土壤有机质含量空间预测方法对比[J]. 地学前缘, 2011, 18(6): 34–40SU X Y, ZHAO Y C, YANG H, et al. A comparison of predictive methods for mapping the spatial distribution of soil organic matter content with different sampling densities[J]. Earth Science Frontiers, 2011, 18(6): 34–40

[20] YANG Q Y, LUO W Q, JIANG Z C, et al. Improve the prediction of soil bulk density by cokriging with predicted soil water content as auxiliary variable[J]. Journal of Soils and Sediments, 2016, 16(1): 77–84

[21] 杨顺华, 张海涛, 陈家赢, 等. 平原丘陵过渡带土壤有机碳空间分布及环境影响[J]. 中国环境科学, 2015, 35(12): 3728–3736YANG S H, ZHANG H T, CHEN J Y, et al. The spatial variability of soil organic carbon in plain-hills transition belt and its environmental impact[J]. China Environmental Science, 2015, 35(12): 3728–3736

[22] 鲍士旦. 土壤农化分析[M]. 北京: 中国农业出版社, 2000: 30–237BAO S D. Soil and Agricultural Chemistry Analysis[M]. Beijing: China Agriculture Press, 2000: 30–237

[23] 司涵, 张展羽, 吕梦醒, 等. 小流域土壤氮磷空间变异特征分析[J]. 农业机械学报, 2014, 45(3): 90–96 SI H, ZHANG Z Y, LU M X, et alSpatial variability of soil nitrogen and phosphorus in small watershed[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(3): 90–96

[24] 张晗, 赵小敏, 欧阳真程, 等. 多尺度下的南方山地丘陵区耕地质量空间自相关分析——以江西省黎川县为例[J]. 中国生态农业学报, 2018, 26(2): 263–273 ZHANG H, ZHAO X M, OUYANG Z C, et al. Multi-scale spatial autocorrelation analysis of cultivated land quality in China’s southern hillside areas: A case study of Lichuan County, Jiangxi Province[J]. Chinese Journal of Eco-Agriculture, 2018, 26(2): 263–273

[25] KUMAR S. Estimating spatial distribution of soil organic carbon for the Midwestern United States using historical database[J]. Chemosphere, 2015, 127: 49–57

[26] 杨其坡, 武伟, 刘洪斌. 基于地形因子和随机森林的丘陵区农田土壤有效铁空间分布预测[J]. 中国生态农业学报, 2018, 26(3): 422–431 YANG Q P, WU W, LIU H B. Prediction of spatial distribution of soil available iron in a typical hilly farmland using terrain attributes and random forest model[J]. Chinese Journal of Eco-Agriculture, 2018, 26(3): 422–431

[27] 孙冬梅, 陈学昌. 黑龙江省土壤有机质与全氮和碱解氮的相关分析[J]. 黑龙江八一农垦大学学报, 1995, 8(2): 57–60SUN D M, CHEN X C. Correlation analysis of soil organic matter, total nitrogen and available nitrogen in Heilongjiang Province[J]. Journal of HAFLRU, 1995, 8(2): 57–60

[28] 罗由林, 李启权, 王昌全, 等. 川中丘陵县域土壤碳氮比空间变异特征及其影响因素[J]. 应用生态学报, 2015, 26(1): 177–185 LUO Y L, LI Q Q, WANG C Q, et al. Spatial variability of soil C/N ratio and its influence factors at a county scale in hilly area of Mid-Sichuan Basin, Southwest China[J]. Chinese Journal of Applied Ecology, 2015, 26(1): 177–185

[29] 许小伟, 樊剑波, 陈晏, 等. 不同有机无机肥配施比例对红壤旱地花生产量、土壤速效养分和生物学性质的影响[J]. 生态学报, 2014, 34(18): 5182–5190XU X W, FAN J B, CHEN Y, et alEffects of combined application of organic and chemical fertilizers on the yield of peanut, soil available nutrient and biological properties in the upland red soil in subtropical China[J]. Acta Ecologica Sinica, 2014, 34(18): 5182–5190

[30] YATES S R, WARRICK A W. Estimating soil water content using Cokriging[J]. Soil Science Society of America Journal, 1987, 51(1): 23–30

[31] 秦鱼生, 涂仕华, 冯文强, 等. 成都平原水旱轮作种植下土壤养分特性空间变异研究[J]. 土壤学报, 2008, 45(2): 355–359 QIN Y S, TU S H, FENG W Q, et al. Spatial variability of soil nutrient characteristics under paddy-upland crop rotation in Chengdu Plain[J]. Acta Pedologica Sinica, 2008, 45(2): 355–359

[32] KUMAR S, LAL R, LIU D S. A geographically weighted regression kriging approach for mapping soil organic carbon stock[J]. Geoderma, 2012, 189/190: 627–634

[33] ERNER Y, COHEN A, MAGEN H. Fertilizing for High Yield Citrus[M]. Basel, Switzerland: International Potash Institute, 1999: 31–35

[34] LAI L, HUANG X J, YANG H, et alCarbon emissions from land-use change and management in China between 1990 and 2010[J]. Science Advances, 2016, 2(11): e1601063

[35] 赵业婷, 常庆瑞, 李志鹏, 等. 基于Cokriging的耕层土壤全氮空间特征及采样数量优化研究[J]. 土壤学报, 2014, 51(2): 415–422ZHAO Y T, CHANG Q R, LI Z P, et al. Study on spatial distribution of total nitrogen in arable soil layer and optimization of number of soil samples for the study based on Cokriging[J]. Acta Pedologica Sinica, 2014, 51(2): 415–422

Prediction of spatial distribution of soil organic matter based on improved OK models: A case study of Honghuatao Town in Yidu City*

DUAN Lijun, GUO Long, ZHANG Haitao**, JU Qinglan

(College of Resources and Environment, Huazhong Agricultural University, Wuhan 430070, China)

Choosing a suitable prediction model to estimate soil organic matter (SOM) content is not only a prerequisite to improve the accuracy of spatial distribution simulation, but also the basis for monitoring dynamic changes in soil carbon pool and for guiding soil fertility input in farming. In order to achieve this, a research was set up to investigate the advantages of combined traditional Ordinary Kriging (OK) interpolation and Co-Kriging (COK) interpolation in constructing a new model that integrates Cooperative Correlation of auxiliary variables with OK model (CCOK). The following three aspects were thus discussed: 1) whether the inclusion of auxiliary variables had an impact on SOM prediction result; 2) what were the differences in SOM prediction results caused by changes in the number of auxiliary information interpolations; and 3) how improved SOM prediction accuracy by cooperative correlation of auxiliary variables. To address these research questions, we collected 329 soil samples from a citrus plantation in Honghuatao Town located in the north Yidu City, Hubei Province. Through physical and chemical analysis, 14 soil properties were extracted. The correlation between SOM and other soil properties were discussed based on Pearson correlation coefficient () and available nitrogen was chosen as model auxiliary variable with the most significant correlation with SOM. With reference of OK (the control), we constructed modeling COK (COK1), global COK (COK2) and two improved OK models (CCOK1and CCOK2). Among the models, COK1was a COK model which used modeling set auxiliary variables to participate in modeling. Based on COK1, COK2changed the modeling set auxiliary variables to global auxiliary variables. CCOK1and CCOK2represented the OK interpolation models of two forms of functions constructed by the target variables and its auxiliary variables. Some of the results obtained were as follows: 1) the range of the nugget/sill proportions of OK, CCOK1and CCOK2were 25%-75%, which belonged to medium spatial autocorrelation. However, the nugget/sill proportions of COK1and COK2were less than 25%, belonging to strong spatial autocorrelation. It then showed that the spatial variability of SOM as cross-variance function with auxiliary variables was more easily recognized by semi-variogram models. 2) The predicted SOM in the study area was within 7.38–29.03 gžkg-1. Compared with OK interpolation, the strong spatial autocorrelation of COK1and COK2meant that the spatial distribution of SOM was even more fragmented. Furthermore, plots of CCOK1and CCOK2predictions were flaky, with digital mapping results of SOM with higher or lower values, which was more consistent with the actual distribution of land use in the study area. 3) The accuracies of COK1and OK were similar, but that of COK2was higher than the above two. Nevertheless, the correlation coefficients () of CCOK1and CCOK2increased from 0.10 to 0.70 and 0.69, with root mean square errors (RMSE) decreasing by 15.40% and 14.78%, respectively. Finally, the overall accuracy of SOM digital soil mapping was CCOK1≈ CCOK2> COK2> COK1≈ OK. This indicated that CCOK model minimized error between measured and predicted values in SOM prediction. Thus, the synergy of combined SOM estimation and auxiliary variables was a better correlation than the addition of only auxiliary variables or changing the amount of auxiliary variables. The improved OK model proposed in this study improved the maximum participation of auxiliary information, thereby providing a reliable reference for SOM prediction.

Soil organic matter; Auxiliary variable; Available nitrogen; Cooperative correlation; Improved OK models; Spatial autocorrelation

, E-mail: hzau_zht@163.com

Apr. 5, 2018;

Jul. 13, 2018

S158.9

A

2096-6237(2019)01-0131-11

10.13930/j.cnki.cjea.180348

段丽君, 郭龙, 张海涛, 琚清兰. 基于改进OK模型的土壤有机质空间分布预测——以宜都市红花套镇为例[J]. 中国生态农业学报(中英文), 2019, 27(1): 131-141

DUAN L J, GUO L, ZHANG H T, JU Q L. Prediction of spatial distribution of soil organic matter based on improved OK models: A case study of Honghuatao Town in Yidu City[J]. Chinese Journal of Eco-Agriculture, 2019, 27(1): 131-141

* 国家自然科学基金项目(41371227)资助

张海涛, 主要研究方向为土壤环境科学。E-mail: hzau_zht@163.com

段丽君, 主要研究方向为土壤环境与生态动态模拟。E-mail: duanlijun@webmail.hzau.edu.cn

2018-04-05

2018-07-13

* This study was supported by the National Natural Science Foundation of China (41371227).