二维拉氏辐射流体力学人为解构造方法*

刘学哲,林 忠,王瑞利,余云龙

(北京应用物理与计算数学研究所,北京 100094)

辐射流体力学在武器物理、惯性约束聚变、磁约束聚变、地质学和天体物理等诸多领域有广泛的应用，描述多物理过程耦合的辐射流体力学方程组具有强耦合、强间断、强非线性等特征，很难得到解析解，利用计算机进行数值求解是重要的研究手段。

数值模拟是否正确求解了方程，模拟结果能否再现真实的物理过程，都需要对数值模拟程序进行验证与确认[1-3]。人为构造解方法[4]是程序验证的重要方法之一，对某些特殊需求(正确性验证、收敛性考察，等)具有不可替代性。在求解双曲型流体力学方程组程序人为解验证方面已有很好的工作[5-14]，但大多基于欧氏方程，对抛物型辐射扩散方程解析解及人为解验证方面也有很多工作[15-16]，而适用于求解辐射与流体耦合方程组及拉氏程序验证的人为解模型尚不多见。

针对拉氏辐射流体力学程序正确性验证的需要，文献[17-18]中构造了一类一维拉氏流体力学和辐射流体力学人为解模型，但一维模型的网格运动仅改变网格点的疏密，不涉及到网格的变形，而网格随流体运动而变形是拉氏计算的特点，因此，构造适应流体大变形的二维拉氏辐射流体力学人为解模型对实际应用程序的正确性验证很有意义。本文中基于二维坐标变换关系式，研究了拉氏辐射流体力学人为解方法，构造了适用于辐射流体力学程序验证的二维人为解模型，并应用于非结构拉氏应用程序LAD2D[19]辐射流体力学计算的正确性考核，取得了很好的效果。

1 二维拉氏辐射流体力学方程组

考虑如下拉氏形式的二维辐射流体力学方程组：

(1)

(2)

(3)

(4)

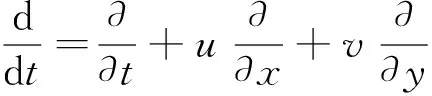
p=pρ,T,e=eρ,T,κ=κρ,T

(5)

和适当的初边值条件，则计算模型封闭。

2 二维拉氏辐射流体力学人为解构造

2.1 二维坐标变换

引入拉氏坐标x0=x0,y0,给定拉氏空间x0,y0,τ到欧氏空间x,y,t的坐标变换关系式：

x=xx0,y0,τ,y=yx0,y0,τ,t=τ

(6)

其微分关系为：

(7)

记Jx0,y0,τ为坐标变换的Jacobi矩阵：

(8)

其行列式记为：

(9)

(10)

为流体速度。

函数ux0,y0,τ、vx0,y0,τ与坐标变换的Jacobi矩阵Jx0,y0,τ应满足Cauchy相容关系：

(11)

下面给出欧氏空间中的空间导数和拉氏随体导数在拉氏空间的表达式。

设物理变量z在欧氏空间关于坐标x,y,t的函数关系为f，在拉氏空间关于坐标x0,y0,τ的函数关系为g，即：

z=fx,y,t=fxx0,y0,τ,yx0,y0,τ,τ≡

gx0,y0,τ=gx0x,y,t,y0x,y,t,t≡fx,y,t

(12)

则有：

(13)

(14)

(15)

而:

即欧氏空间的拉氏随体导数就等于拉氏空间的时间导数：

(16)

2.2 二维拉氏辐射流体力学人为解构造方法

从拉氏计算中使用的二维拉氏辐射流体力学方程(1)～(5)出发，给定位移解函数和温度解函数，利用二维坐标变换关系式，由无源项的质量方程解出密度解函数，再将已知解函数代入动量方程和能量方程，残余项视为方程源项。具体构造过程如下:

(1)给定位移解函数x=xx0,y0,τ，y=yx0,y0,τ和温度解函数T=Tx0,y0,τ。

(2)根据式(9)和(10)，由位移解函数x=xx0,y0,τ,y=yx0,y0,τ,可计算出坐标变换Jacobi行列式J=Jx0,y0,τ和流体速度u=ux0,y0,τ,v=vx0,y0,τ。

(3)解连续性方程求出密度解函数。

利用空间导数关系式(15)和Cauchy相容关系式(11)求出速度散度：

(17)

代入连续性方程(1)，并利用欧氏空间的拉氏随体导数与拉氏空间的时间导数之间的关系式(16)，得：

(18)

式中：ρ0x0,y0=ρx0,y0,0，J0x0,y0=Jx0,y0,0。

(4)根据温度解函数确定动量方程源项和内能方程源项。

由动量方程(2)～(3)导出源项：

(19)

根据时间导数关系式(16)和空间导数关系式(15)，可得：

(20)

(21)

由(18)式可得：

(22)

(23)

其中用到了状态方程关系式(5)：

px0,y0,τ=pρx0,y0,τ,Tx0,y0,τ

由内能方程(4)，导出源项：

(24)

利用时间导数关系式(16)、速度散度表达式(17)和空间导数关系式(15)，得：

(25)

其中用到了状态方程关系式(5)：

ex0,y0,τ=eρx0,y0,τ,Tx0,y0,τ,κx0,y0,τ=κρx0,y0,τ,Tx0,y0,τ

3 二维拉氏辐射流体力学程序验证

3.1 拉氏辐射流体二维人为解模型

为方便计，在不致引起混淆的情况下，时间变量统一用t表示。

由上节的人为解方法可知，选择不同的位移解函数和温度解函数，可以构造出不同的人为解模型。

给定计算区域:

0≤x0,y0≤1； 0≤x,y≤1； 0≤t≤1

和状态方程:

p=0,e=cVT,κ=k0cV=1，κ0=1

选择位移解函数：

xx0,y0,t=x0+x01-x0bsin2πtcosπy0,

yx0,y0,t=y0+y01-y0bsin2πtcosπx0b=0.8

和温度解函数:

T=Tx,y,t=T1+sin2πxcos(2πy)T1=2

初始密度:

ρ0x0,y0=ρ0=1

则可推导出以下。

(1)坐标函数初、边值：

0≤x0≤1， 0≤y0≤1

xlefty0,t=0,xrighty0,t=1，ytopx0,t=1,ybottomx0,t=0 0≤t≤1

且:

xlefty0,t0=x0left=0，xrighty0,t0=x0right=1，ytopx0,t0=y0top=1,ybottomx0,t0=y0bottom=0

式中：xleft、xright、ytop、ybottom分别为计算区域的左、右、上、下边界。

(2)坐标变换Jacobi行列式：

1+(1-2x0)bsin2πtcosπy01+(1-2y0)bsin2πtcosπx0-

πx01-x0bsin2πtsinπy0πy01-y0bsin2πtsinπx0

不难验证，当0≤x0≤1，0≤y0≤1，00;当t=0时，J(x0,y0,t)=1。

(3)速度解函数：

ux0,y0,t=2πx01-x0bcos2πtcosπy0

vx0,y0,t=2πy01-y0bcos2πtcosπx0

(4)密度解函数：

(5)压力解函数：

px0,y0,t=0

(6)比内能解函数：

ex0,y0,t=T

(7)内能方程源项：

cos2πxcos2πyx01-x0cosπy0-sin2πxsin2πyy01-y0cosπx0+

8π2k0sin2πxcos2πyJ

(8)动量方程源项：

(9)边界条件。

流体为固壁边界条件：

ulefty0,t=0，urighty0,t=0，vtopx0,t=0,vbottomx0,t=0

辐射左右边界为第一类边界条件，上下边界为第二类边界条件：

不难看出，构造的人为解满足保正的物理条件，即对任意的:

x0,y0,t∈xleft,xright×ytop,ybottom×R+

都有:

Jx0,y0,t>0，ρx0,y0,t>0，Tx0,y0,t>0，ex0,y0,t>0

3.2 二维拉氏辐射流体力学LAD2D程序正确性验证

将构造的人为解模型应用于二维非结构网格拉氏辐射流体力学应用程序LAD2D[19]的正确性验证。

初始时，计算区域均匀划分为32×32的方形网格，人为解中参数b=0.8，取固定时间步长Δt=7.812 5×10-4，计算到t=1.0时刻。

由构造的人为解位移解函数可知，它为关于时间t的周期函数，这里选取了t=0，0.125，0.25等3个典型时刻，图1给出了不同时刻流体运动网格图。

图1 不同时刻流体运动网格Fig.1 Fluid meshes at different times

图2给出了t=0.125时刻流体网格上的密度、温度、x方向速度、y方向速度的数值解和人为精确解的等值线，红线为数值解，绿线为人为精确解，两者基本一致，验证了程序辐射流体求解的正确性。

图2 t=0.125时刻流体运动网格上密度、温度、x方向速度、y方向速度等值线(红：数值解 绿：精确解)Fig.2 Contours of density, temperature, x and y components of velocity(red: numerical solution; green: exact solution)

通常的扩散方程求解，无论是正交网格还是大变形扭曲网格，求解过程中网格始终保持不变，在二维运动网格上考察扩散问题目前尚未见文献报道。由本文人为解构造可知，通过设定特殊形式的状态方程(p=0)，可以在流体运动网格上求解扩散模型。 图3给出了不同时刻流体运动网格上温度数值解和人为精确解的比较，红线为数值解，绿线为人为精确解，从图中可以看出，从初始时刻开始，网格在不断运动，网格变形程度逐渐增大，而我们构造的温度解函数在欧氏空间来看不随时间变化，数值解较好地保持了精确解的这一性质。

图3 不同时刻流体运动网格上温度等值线(红：数值解 绿：精确解)Fig.3 Contours of temperature on fluid meshes at different time (red: numerical solution; green: exact solution)

进一步考察人为解的数值收敛性，在不同的网格规模下，网格比Δt/Δx2=0.8保持不变，计算到t=1.0时刻，表1给出了温度的误差收敛性分析。数值结果显示温度L2模和最大模误差二阶收敛，验证了计算结果与理论分析的一致性。

表1 温度收敛误差和收敛阶Table 1 Convergence errors and orders for temperature

4 结 论

从拉氏计算中使用的辐射流体力学方程组出发，基于二维坐标变换技术，研究了一类质量方程无源项，动量方程和能量方程包含源项的人为解构造方法，构造了一类适用于辐射流体力学程序验证的二维人为解模型，并应用于非结构拉氏程序LAD2D辐射流体力学计算的正确性考核，为流体运动网格上的辐射扩散计算提供了新的途径。