深度连续渐变式空腔阵列表面发射率研究

王潇楠，李文军，李佳琪，郑永军

（中国计量大学计量测试工程学院，浙江杭州310018）

1 引 言

发射率作为一项非常重要的热物性参数，能够表征材料的辐射能力［1］。在辐射传热学中，材料辐射出度、辐射照度以及功率的计算都与材料的发射率息息相关。发射率的测量研究不仅有利于加热技术中涂料的研制，而且还能为辐射测温和热成像技术提供必不可少的理论数据［2］。有学者提出了空腔效应，由辐射性能一致的漫射表面组成的腔体，其辐射行为可以由腔体开口的表现来描述［3］，所以需要使用类似空腔来提供稳定的发射率分布。而发射率作为表征物体表面热辐射特性的物理量，与物体的温度有很大关系。因此，精确地确定物体的热辐射与其温度之间的关系有助于实现辐射测温技术的发展［4-7］。温度作为一个基本的物理量，其测量方法多种多样，可分为接触式测温法和非接触式测温法。非接触式测温法主要以辐射测温法为主［8-11］。

依据文献中提出的梯度发射率测试与校准，该文首先介绍了一种深度连续渐变式空腔阵列作为发射率的样品，提供了发射率计算方法，然后介绍了红外热像仪与发射率样品组成的实验装置，在实验室环境下进行不同温度下不同空腔深度表面发射率测试实验，最后分析验证了结果，得出温度和空腔深度对表面发射率影响的结论。

2 表面发射率的计算分析

为克服现有发射率样品不足的现状，该文设计了一种深度连续渐变式空腔阵列，如图1所示。该空腔阵列的表面在法向具有稳定的发射率分布，可提供不同发射率的表面单元。

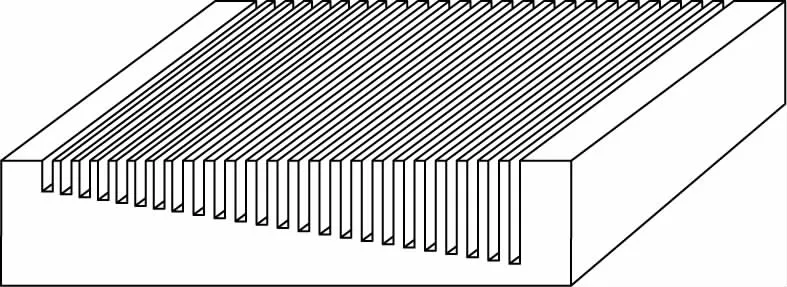
图1 深度连续渐变式空腔阵列示意图Fig.1 Depth continuous gradient cavity array

选取高导热性的金属作为基底，在金属基底的上表面切割多个矩形槽，矩形槽的深度连续渐变。当金属基底材料发射率稳定时，单个矩形空腔表面的发射率主要取决于矩形槽和矩形翅的几何形状。因此，在深度连续渐变式空腔阵列的上表面连续选取不同的区域，可以获得具有稳定且各不相同的发射率的表面单元。

2.1 斯蒂芬-波尔兹曼定律

斯蒂芬-波尔兹曼定律描述了任意温度为T的绝对黑体，单位面积上在整个半球方向所发射的全波长辐射强度E与温度T的关系：

式中，σ为斯蒂芬-波尔兹曼常数；T为物体热力学温度。T为黑体的表面温度，也就是实际物体的辐射温度。但通常的物体都不是理想黑体，而是灰体，此时可用下式来表示实际热辐射强度E与温度T之间的关系：

2.2 单元表面发射率的计算

深度连续渐变式空腔阵列由多个深度连续渐变的矩形空腔组合形成，矩形空腔的结构示意图，如图2所示。

图2 矩形空腔结构示意图Fig.2 Schematic diagram of rectangular cavity

当连续选取n个矩形空腔时，选取的区域形成一个单元，单元表面发射率εe可以用式（3）表示：

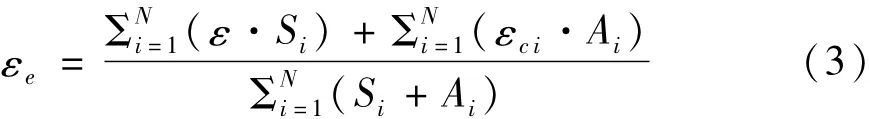
式中，εci为第i个矩形槽的表面发射率；Si为第i个矩形槽槽面的面积；Ai为第i个矩形翅翅面的面积。

引入槽翅宽比k=a/b，则有：

将公式（4）代入公式（3）中，空腔阵列单元表面发射率εe可以简化为以下公式：

2.3 单元表面发射率的分布

随深度渐变，渐变倾斜角度能够对矩形槽的深度造成影响。倾斜角度不同，各个矩形槽的深度也将不同，从而影响矩形槽的发射率分布规律，如图3所示。

图3 深度连续渐变式空腔阵列倾斜角示意图Fig.3 Inclination angle of depth continuous gradient cavity array

当倾斜角度为θ时，利用三角函数关系式可以得到相邻两个矩形槽的深度之间的关系为：

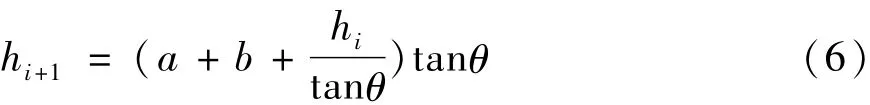
式中，a为矩形槽宽度；b为矩形翅宽度；hi为第i个矩形槽的深度；hi+1为第（i+1）个矩形槽的深度。

3 表面发射率的实验测量

随着新型的辐射测温仪和红外测温仪的普及，通过非接触测量温度的方法得到了越来越广泛的应用。一般来讲，如果建立了辐射测温的模型，能够获得物体真实温度的为前提的发射率。

3.1 实验原理

采用ASTM E1933-99a提供的接触式测量法。该方法的测量原理为使用接触式温度计和红外测温设备对同一测量区域进行温度的测量，然后匹配这两个值来确定这一区域的表面发射率［12］。

3.2 实验装置

在实验室环境下搭建了发射率测量的实验装置，主要由加热器、发射率样品、热电偶和红外热像仪组成，实验装置示意图如图4所示。

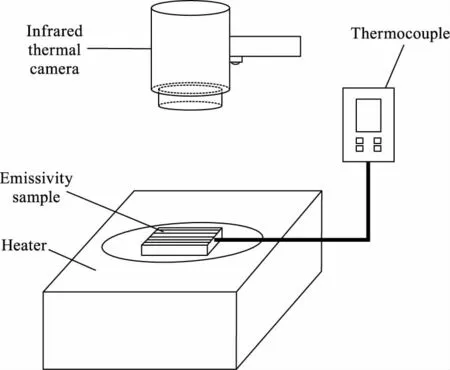
图4 实验装置示意图Fig.4 Schematic diagram of experimental device

实验采用FLIR公司生产的型号为FLIR E60的红外热像仪。它为手持式设计，也可以通过三脚架固定，携带及使用都很方便。技术参数方面，它的红外探测器具有很广的测温区间，能精确测量-20～+650℃范围内的温度值，误差仅为±1℃。这款红外热像仪可以多点测温，它能提供76800个点的温度数据，从而汇成一张分辨率为320×240像素的红外热图像。

3.3 实验步骤

实验装置如图5所示，实验时保持环境温度不变，将被测样品放置在加热器的加热面上进行加热。设定加热器的目标温度，待加热器显示温度达到目标温度后保持10 min，以保证被测样品达到热平衡，再用热电偶测量出被测样品表面的真实温度。然后设置红外热像仪的基础参数，镜头垂直于被测样品表面并保持测量距离在1 m以内，对着被测样品表面拍摄热图像。设定不同的加热目标温度，可以得到被测样品在不同温度点上的发射率。

图5 实验装置Fig.5 Experimental device

在某一个温度点上，具体测量步骤描述如下：（1）首先将红外热像仪发射率设置为1，透射率设置为1，环境温度设置为此时的环境温度。

（2）将红外热像仪镜头垂直于被测样品表面并保持测量距离在1 m以内。

（3）使用红外热像仪的点温、十字线瞄准和等温线功能，测量和补偿由于反射温度所引起的误差。

（4）用表面热电偶测量被测样品的真实温度，并记录。

（5）使用红外热像仪拍摄被测样品表面的热图像。

（6）使用FLIR TOOLS软件处理热图像，调整热像仪发射率，直到热像仪图像指示温度与步骤（4）中温度值相同。记录这时的发射率值，作为被测样品表面在该目标温度下的发射率。

4 表面发射率的实验结果及分析

选取长度60 mm、宽度30 mm、高度10 mm的铝块作为基底材料，使用电火花线切割技术开槽［13］。矩形槽宽度为0.5 mm，矩形翅宽度为0.5 mm，矩形槽初始深度为0.5 mm，倾斜角度为7°。为形成各向同性表面，样品表面涂覆金属涂层铬，涂层发射率为0.3，实物如图6所示。

图6 发射率样品Fig.6 Emissivity sample

4.1 实验结果

在加热温度为 30℃，50℃，70℃，90℃，110℃，130℃和150℃时分别对样品拍摄热图像。样品在加热温度30℃，70℃，130℃时的热图像分别如图7～图9所示。

使用FLIR TOOLS软件对实验所得的热图像进行处理，在热图像表面等段距离连续选取5个单元，每个单元矩形空腔数量均为3槽3翅组合，5个单元分别用单元 B×1、单元 B×2、单元 B×3、单元B×4、单元B×5表示。

图7 样品在加热温度30℃时的热图像Fig.7 The thermal image of the sample at 30℃in heater

图8 样品在加热温度70℃时的热图像Fig.8 The thermal image of the sample at 70℃in heater

图9 样品在加热温度130℃时的热图像Fig.9 The thermal image of the sample at 130℃in heater

由此可得不同温度条件下5个单元表面发射率值见表1。

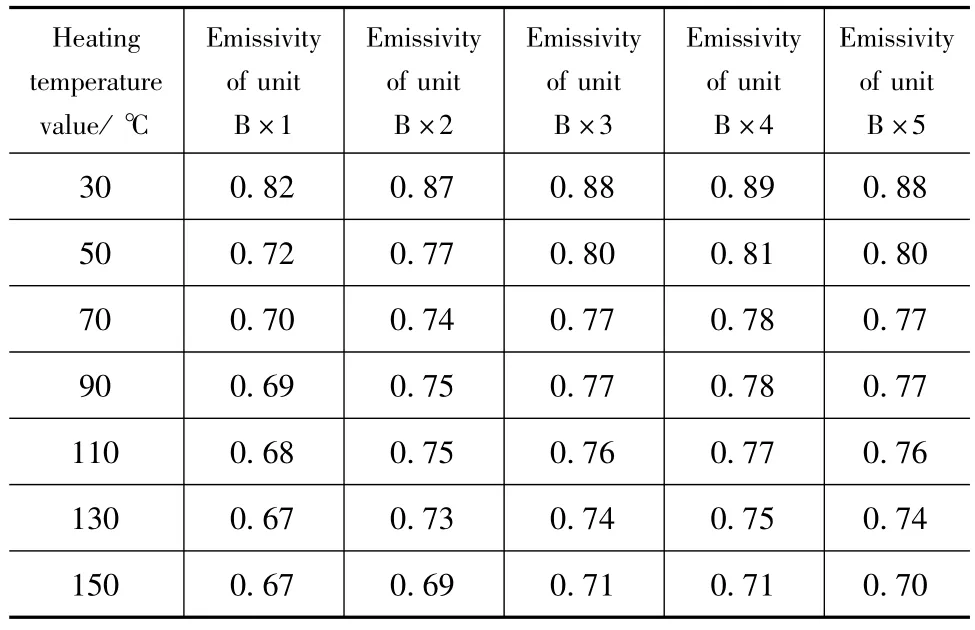
表1 不同加热温度下表面单元发射率Tab.1 Surface emissivity of surface at different heating temperatures

不同加热温度下表面单元发射率变化如图10所示。

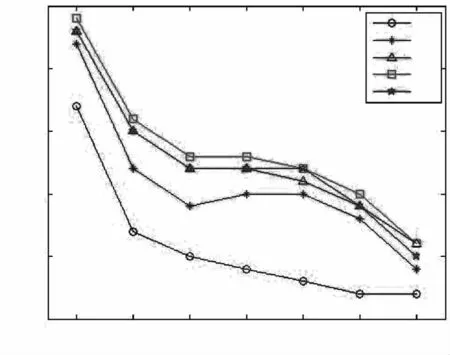
图10 不同加热温度下表面单元发射率变化Fig.10 Change of emissivity of surface at different heating temperatures

4.2 实验分析

从图10中可以看出，在实验加热温度范围内所测样品5个单元的单元表面发射率随加热温度升高而降低，将7种温度下所测单元表面发射率的平均值作为实验测量值。计算得到单元B×1的实验测量值为0.707，理论计算值为0.607；单元B×2的实验测量值为0.757，理论计算值为0.795；单元B×3的实验测量值为0.776，理论计算值为0.861；单元B×4的实验测量值为0.784，理论计算值为0.895；单元B×5的实验测量值为0.774，理论计算值为0.915。将样品单元表面发射率实验测量值与理论计算值按公式（7）得出实验的相对误差δ。

式中，εa为实验测量的平均发射率；εr为理论计算的参考发射率。

计算得到单元B×1的相对误差为16.47%，单元B×2的相对误差为4.78%，单元B×3的相对误差为9.88%，单元B×4的相对误差为12.40%，单元B×5的相对误差为15.41%。

5 结束语

设计制作深度连续渐变式空腔阵列，将不同温度下不同区域表面发射率理论计算值与实验测量值进行比较。随着加热温度的升高和深度的渐变，5个单元表面发射率波动变化趋势基本一致。结果表明，（1）随着加热温度的升高，深度连续渐变式空腔阵列的表面发射率会小幅下降，在加热温度30℃至70℃时下降的较为明显；（2）随着空腔深度的增加，深度连续渐变式空腔阵列的表面发射率会随之增加，其增加的幅度会先增大后缩小；（3）深度连续渐变式空腔阵列表面在法向具有稳定的发射率分布，可提供不同发射率的表面单元。