大型工件单目结构光三维扫描方法

陈思豪，王中任，肖光润，晏 涛

（1.湖北文理学院机械工程学院，湖北襄阳441053；2.武汉科技大学机械自动化学院，湖北武汉430081）

1 引 言

随着测量手段和技术的不断发展，测量要求和测量场景的多样化，物体的三维轮廓测量技术发展迅速，己经广泛应用于测绘测量、产品的逆向工程、模具设计等多个领域［1］。许多具有复杂曲面形貌的大尺寸零部件需要三维实体数字化测量。而视觉测量法由于具有非接触、自动化程度高、速度快、高精度等优点而成为受欢迎的测量技术之一［2］。目前的视觉三维重构多使用双目视觉完成，即利用实际点在两个相机图像上不同位置来确定该物体的三维轮廓［3］。但由于该系统较为复杂，处理速度较慢，很难在工业实际上运用［4］。本文所研究的三维测量系统，则是以单目线结构光来完成，线激光垂直投射于待测表面，图像采集设备和线激光的位置关系相对固定，利用移动平台带动物体运动，实现线激光对被测物体表面的全扫描，对相机拍摄到的线激光在被测物体表面的变形图像进行分析和计算，最终重建被测物体表面的三维轮廓。该方法具有结构简单、处理速度快、精度高等优点，让其在工业实际中有更广泛的应用［5］。

2 系统基本结构

线结构光三维视觉测量系统主要由硬件系统和软件系统组成。硬件系统主要由CCD摄像机、线结构光激光器、图像采集卡、计算机、工作台及其控制器等组成。软件系统按操作顺序主要分为三部分：摄像机的标定、光平面的标定、工件的扫描测量。

系统工作流程如图1所示。首先，计算机通过控制视觉传感器（相机和激光器）来采集结构光效果较好的图像。随后将采集到的图像传入软件系统进行处理，获取结构光线中心的图像坐标。接着将标定获得的模型参数代入传感器数学模型，计算被测物表面点的空间坐标。最后，结合测量模型和输入的运动参数，在设计的数据处理算法下，对测量点坐标进行计算处理即可得到工件真实尺寸。

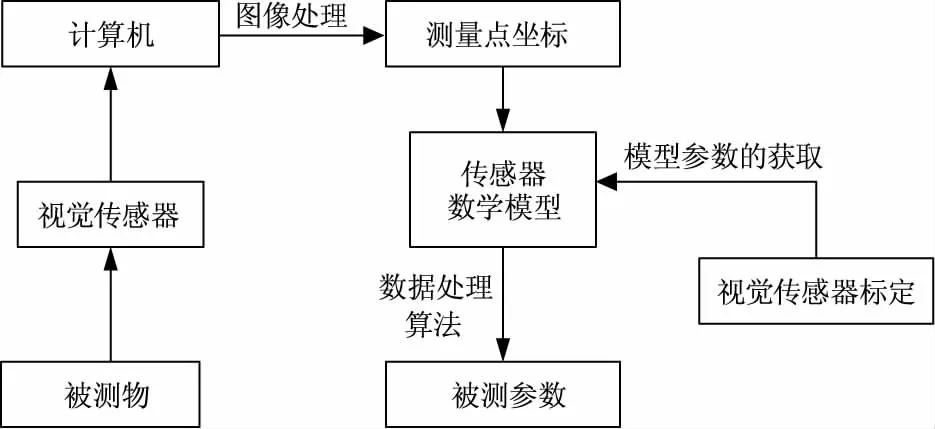
图1 系统工作流程Fig.1 System flow

3 单目线结构光三维测量原理

单目线结构光的测量原理主要是采用了激光三角法的测量原理［6］，其大致的测量过程如图2所示：激光器向被测物体表面投射一个激光光条，由于被测物体表面的形貌特征不同，CCD摄像机拍摄的光条图像中光条中心成像的位置也发生改变。根据激光束光轴与摄像机光轴之间的夹角（30°～60°）以及光条中心在CCD摄像机像平面上的成像位置变化，通过三角几何关系即可获得被测物体表面起伏距离。当然，在实际测量系统中还需有一个稳定的移动平台，保证光平面能够以一恒定的速率扫过整个测量物体，这样才能得到较为准确的物体表面轮廓信息。

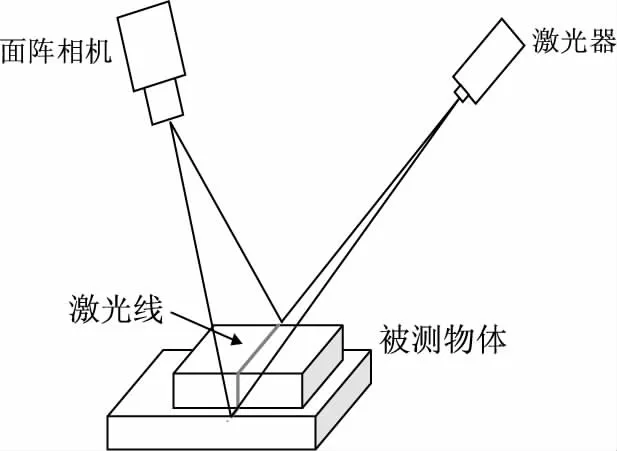
图2 激光三角法测量模型Fig.2 Laser triangulation measurement model

为了得到被测工件准确的三维信息，需建立单目线结构光数学模型［7］。线结构光传感器的激光器在空间上投射出一个光平面，此光平面通过摄像机建立与像平面的透视对应关系，其几何结构关系的数学模型如图3所示。

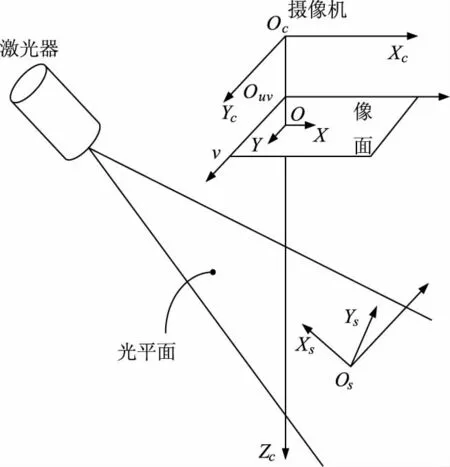
图3 单目线结构光数学模型Fig.3 Optical mathematical model of monocular line structure light

光平面和被测物体相截为一条平面曲线，曲线上的点即为被测的对象。在光平面上以一点Os为原点，建立传感器的测量参考坐标系Os-XsYsZs，其中光平面为Os-XsYs平面。由此可得线结构光传感器的数学模型表达式：

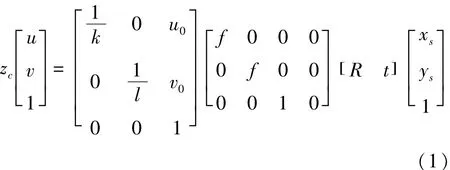
4 实验过程与结果

自主搭建的三维扫描系统采用acA2500-14gm GigE摄像机，分辨率为500万像素，镜头为Computar工业镜头，焦距为8 mm。激光器选用MFL-670-5-65线结构光激光器，波长为650 nm。待测物置于高精密手动平移台上，由剪式升降台调整好合适的的高度，两者都由水平运动平移台所承载，如图4所示。

图4 结构光扫描平台Fig.4 Structured light scanning platform

根据上面的模型，采用检测系统不动，首先由高精密手动平移台沿法向运动完成标定后，再由电控位移台承载待测物体进行匀速运动完成三维扫描。

下面对整个系统进行标定，首先进入摄像机标定模式对相机的位姿进行标定，标定板采用60 mm×60 mm的圆形平面靶标。将靶标面正对摄像机放置，利用精密平移台带动靶标以5 mm的间距移动，一共6次，每个位置都采集一幅图像并获取其位置坐标，如图5所示。

然后经过标定程序运算，得到相机的内部参数：

有效焦距f=8.318749；

畸变系数K1=0.00542；

比例因子Sx=1.004873；

中心坐标Cx=1326.761996；

中心坐标Cy=1142.14376；

象元尺寸dx=0.002200；

象元尺寸dy=0.002200；

接着对线结构光进行标定，进入线结构光标定模式，标定板采用60 mm×60 mm的平行线靶标。与相机标定不同，线结构光标定将靶标面正对激光器放置（即与相机有一个倾角），利用高精密手动平移台带动靶标以5 mm的间距移动，一共6次，每个位置都采集一对激光器开启和关闭的图像。

图5 靶标采集Fig.5 Target acquisition

图6 靶标图像采集Fig.6 Target image acquisition

对所采集到的图片进行预处理，图6是激光开启和关闭状态下分别采集的两幅靶标图像。在处理过程中，为了减少不必要的运算量，提高程序运行的效率，在图像上设定了一定的ROI区域，只在该区域中才对图像进行处理。对开启激光靶标图像进行半二值化处理，即：

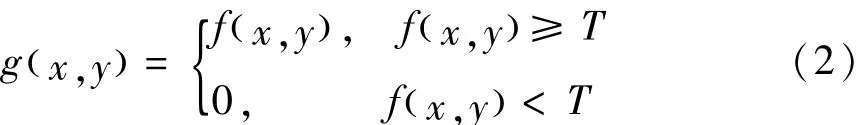
式中：g( x ，y)为处理后图像在点 ( x ，y)处的灰度值；f( x ，y)为原始图像的灰度值，其中T为该算法分割获取的最佳分割阈值。将小于设定阈值的像素点灰度设置为0，大于设定阈值的像素点灰度则保留原有值，从而得到去除背景的光条图像。

对光条图像逐列进行灰度重心提取，获得光条中心像素坐标点集Pli（udi，vdi）。对关闭激光靶标图像进行二值化处理，获得平行线图像。在图像中搜索确定每条平行线的位置区域，对它们逐行进行灰度重心提取，获得每条平行线中心像素坐标点集Pti（udi，vdi）。

最后，为了获取准确特征点的像素坐标，本次实验采用PCA主成分分析方法［8］对由像素点集Pli、Pti组成的图像进行直线拟合，从而获取更准确的特征点坐标。PCA方法是一种非常高效的统计方法，常应用于人脸识别和图像压缩等，采用协方差矩阵理论确定高维空间中的数据模式。在用于二维直线拟合时，该法的运算采用简单的统计和矩阵运算，不必求解方程的偏导，因此，相对于最小二乘法来说，它更简单和稳定可靠。下面介绍一下主成分分析法拟合直线的原理。

假设N个点的二维坐标分别（xi，yi）为，它们的平均中心点坐标为（x，y），由协方差公式：

可以构造协方差矩阵：

求解矩阵C的特征值和特征向量，找到其中最大的特征值对应的特征向量，即为要拟合的直线的法向矢量n→（a，b），将中心点坐标代入直线方程ax+by+c=0，可以确定直线方程的第三个分量c。从而得到特征点的像素坐标，如图7所示。

图7 特征点坐标Fig.7 The coordinates of the feature points

最后根据平移台的移动量和靶标的拓扑关系确定特征点的测量坐标系二维坐标，将其代入两种传感器数学模型，计算出相应的模型参数，完成相机的标定。图 8为平移距离分别在 0.000 mm、10.000 mm和25.000 mm处的光条图像。可见，在平移过程中光条在图像上的位置发生了偏移，在摄像机视场范围内存在13个特征点，标定过程中共移动了6个位置。

图8 三处平移位置的光条图像Fig.8 Lightstripe images at three translation positions

接着根据线结构光标定程序运算，得到线结构光的标定参数：

最后进入工件扫描测量模式，以一大型铸铝件为被测对象。为提高程序运行速度与精度，现在视野中选取一块能包含全部有效轮廓信息的区域，去除了其余无效的区域。利用线结构光原理提取大型铸铝件的三维轮廓信息。

在实验过程中，为了能在最短的时间内获取符合精度要求的三维重构图像，提高工业应用的效率。现使待测物处于不同扫描速率下，通过重构出的三维点云数据及误差的分析，来选取最合适的扫描速度。

现采用0.5～2.0 mm/s的速度对该大型铸铝件进行扫描，所得的结果如表1所示。

从表1可以清晰地看出，当扫描速度小于1.25 mm/s时，三维重构过程中所得点的个数虽然有很大增长，但其平均误差却都趋近于0.08 mm，变化幅度不大。而当扫描速度超过1.4 mm/s时，其所获得的点的个数大大降低，平均误差也快速增大。而在1.25～1.40 mm/s之间，由于后二者误差太过接近0.1 mm，因此最终选用1.25 mm/s的扫描速度，此时得到如图9所示的三维点云图，一共包含约210万个点。

表1 扫描速度与误差Tab.1 Scanning speeds and errors

图9 三维点云图Fig.9 3D point cloud

将三维点云图进行封装处理，得到如图10所示的三维模型图，与原CAD模型进行对比，其平均误差为0.0835 mm，小于0.1 mm，满足了测量所需的精度要求。

图10 三维模型图Fig.10 Three-dimensional model diagram

4 结 语

本文利用自主设计的激光视觉传感系统研究了对大型工件的三维重构，简单有效且重构精度高。采用精密平移台托载平行线靶标对相机和光平面进行标定，并使用PCA主成分分析法完成特征点的直线拟合，得到精确的模型参数。接着，使用水平平移台托载工件运动得到稳定易重构的工件扫描图，完成三维模型的建立。最后通过对扫描速度和重构精度的实验验证，选取了合适的扫描速度。经与被测物尺寸对比，此种方法能够有效准确的对大型工件表面进行三维重构，具有较高的精度及较快的速度，能够满足工业应用的基本要求。