渔网机张力控制技术研究*

王 飞，顾寄南，唐仕喜

(江苏大学 制造业信息化研究中心，江苏 镇江 212013)

0 引 言

渔网机网片由纬线与经线编织而成，纬线与经线的张力控制对于渔网机张力控制很重要。对于经线而言，当卷绕过程中张力过小，网片会时紧时松，并且网片的结的大小、位置以及网目大小也会参差不齐。若卷绕过程中张力过大，会使得经线绕着卷辊产生相对滑动，影响线的表面质量甚至导致网线拉断。

张力控制系统本身具有不确定性，经线缠绕时具有一定的弹性，卷绕半径、卷入速度随时间不断变化，张力设定值变化等都使得系统数学模型发生很大变化[1-3]。同时系统受随机干扰因素的影响，如缠绕过程中设备抖动、电机力矩输出不均性、伺服电机的电信号干扰等。系统还会受到多种非线性因素的影响，如轴辊与轴承之间的静摩擦。由于非线性因素的存在，张力控制系统的数学模型与实际偏差较大。

因张力控制系统受多种因素干扰，导致传统PID控制精度难以达到要求。而模糊理论控制适用于非线性[4]、有时变和滞后特点的控制系统。

本文将采用模糊PID控制方法，对张力控制系统的多变量、非线性、时滞性等进行研究，对渔网机经线张力数学模型以及张力波动的主要影响因素进行分析。

1 张力控制模型

张力控制目的是确保经线卷绕张力恒定。采用传统PID控制方法，设定一组固定P，I，D参数，由于这些参数同时具备动态和静态属性，在收卷过程中，随着半径增加，其惯性也在增加，并且由于切换速度转换技术不同，传统的PID控制系统往往无法达到最佳效果[5]。

在渔网机张力控制系统中，收卷部分半径不断增加，卷径变化是个明显的扰动量。经线与辊轮之间为滚动摩擦，不存在滑动摩擦。主电机辊速度保持不变，其两侧收卷部分与放卷部分张力不相等，本研究对张力收卷控制部分进行分析。收卷部分的调节辊是张力的反馈环节，经线张力发生波动，调节电机输出力矩不变，张力的波动带动摆杆位置发生变化后调节电机反馈力矩发生改变，并将该反馈信号传到PLC中。PLC将反馈力矩与设定值比较并结合卷径的变化得出计算结果控制收卷电机转速，实时动态调整收卷辊转速保证张力的稳定。

张力控制结构如图1所示。

图1 张力控制结构

以收卷辊为研究对象，根据力矩平衡原理，得到经线上的张力、收卷电机转矩、阻力转矩、摩擦力矩之间的关系如下：

(1)

张力通过调节辊反馈到调节电机转矩关系为：

(2)

式中：T—经线张力;R—实时卷绕半径;Mm—收卷电机转矩;Me—摩擦力矩;MB—调节电机的力矩;Mt—阻力转矩;J—线卷的实时转动惯量;w—角速度。

根据方程，卷径R、线卷转动惯量J以及角速度w都是时间的函数，因此该系统是多变量的时变系统。

其中，J由卷轴及网线转动惯量组成：

(3)

式中:JR—卷网线的转动惯量;Jr—卷轴的转动惯量;ρ—网线材料密度;b—线卷宽度;ρ0—卷轴材料密度;R—实时线卷半径;r—实时芯轴半径。

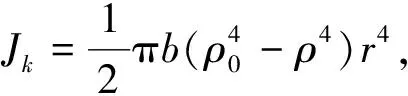
(4)

实际生产过程中，随着收卷的不断进行，收卷半径不断增大，收卷电机根据调节电机转矩不断调整收卷速度v，收卷速度v为非线性变化。角速度w关系为：

(5)

其中：

(6)

假设单位时间内卷侧面积的变化为ds，h为网线厚度，且厚度很小，则：

ds=hv·dt=2πR·dR

(7)

(8)

该系统中摩擦力很小，为了简化模型将其忽略不计，将公式(3～8)代入到(1)中得到：

(9)

通过上式可以看出：在收卷部分在线速度v、收卷电机转矩Mm、阻力矩Mt保持不变的情况下，卷绕张力会随着卷径R的不断变化而产生波动，卷绕半径以及收卷转速成为影响张力控制主要因素，实际工作中还存在其他因素影响。由于系统参数具有不确定性，卷绕半径通过公式计算得到，本身存在一定误差[6]。采用传统PID控制方法较难直接通过张力模型来实现对张力的控制。

将常规PID与模糊推理进行结合，利用模糊逻辑推理实现PID控制器参数的在线整定，可以有效实现对张力的稳定控制[7-8]。

2 模糊PID控制

2.1 张力系统传递函数

本研究以收卷辊部位的伺服电机为执行元件，调节电机的反馈力矩通过转换得到张力并反馈到PLC中，PLC根据计算结果控制收卷伺服电机转速，维持经线张力值不变。在不考虑随机干扰的影响时，系统的传递函数结构如图2所示。

图2 模糊PID控制结构Ga(s)—收卷伺服电机的传递函数，可简化为一个比例环节和一个惯性环节;R—卷绕半径;Gb(s)—摆杆传递函数;Gc(s)—调节电机根据摆杆位置转成反馈力矩大小，可看成比例环节。

在实验条件下，取卷绕半径0.05 m，根据两点法所测系统的传递函数为：

(10)

2.2 隶属度函数

模糊控制器的两个输入为卷绕张力的偏差E与偏差变化率EC，而输出为PID控制器的3个参数：kP、kI、kD的变化量[9]。系统实现自调整PID参数的计算公式为：

kP=kP0+ΔkP

(11)

kI=kI0+ΔkI

(12)

kD=kD0+ΔkD

(13)

式中：kP0，kI0，kD0—P、I、D的初始值；ΔkP，ΔkI，ΔkD—模糊控制器的输出，kP、kI、kD为最终控制输出参数。

偏差E以及偏差变化率EC作为本研究的模糊控制系统的输入语言变量。将其离散化为7个等级，分别为负大、负中、负小、零、正小、正中、正大，简写为{NB,NM,NS,ZO,PS,PM,PB}，论域为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}；ΔkP，ΔkI，ΔkD的论域为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}，模糊子集为{NB,NM,NS,ZO,PS,PM,PB}[10]。

常用隶属度函数主要有：单值型、三角形、高斯型等。单值型的隶属度函数无法解决输入变量里存在的噪声信号问题，而高斯型隶属度函数计算较为复杂。本研究选择三角形隶属度函数，不仅可以减少计算量，也可以克服输入变量中的噪声信号[11]。偏差E、偏差变化率EC和输出变量ΔKp，ΔKi，ΔKd均选择三角形隶属度函数。

以E的隶属度函数为例，如图3所示。

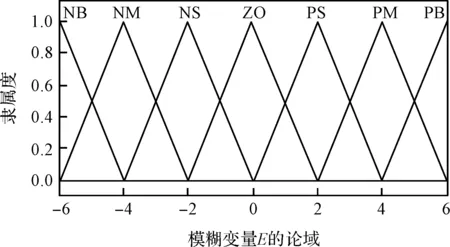
图3 输入变量E的隶属度函数

2.3 模糊PID控制与规则表

根据工程设计知识和工程师操作经验，建立对渔网机控制器的调节规则：

(1)收卷开始阶段，整个设备的震动较大，张力的波动也较大，因此张力的偏差|E|较大，此时应当适当减少ΔkP、ΔkI，同时增大ΔkD，避免出现张力输出的积分饱和与超调现象；

(2)系统趋向稳定运行时，张力波动较小，|E|接近于中等值，此时应适当增加ΔkP、ΔkI，同时ΔkD取中等偏小值，以提高系统的稳定性与响应速度；

(3)系统稳定运行时，张力的波动几乎为零，此时应减小ΔkP，增大ΔkI，以减小静态误差。

输出变量控制规则表如表1所示。

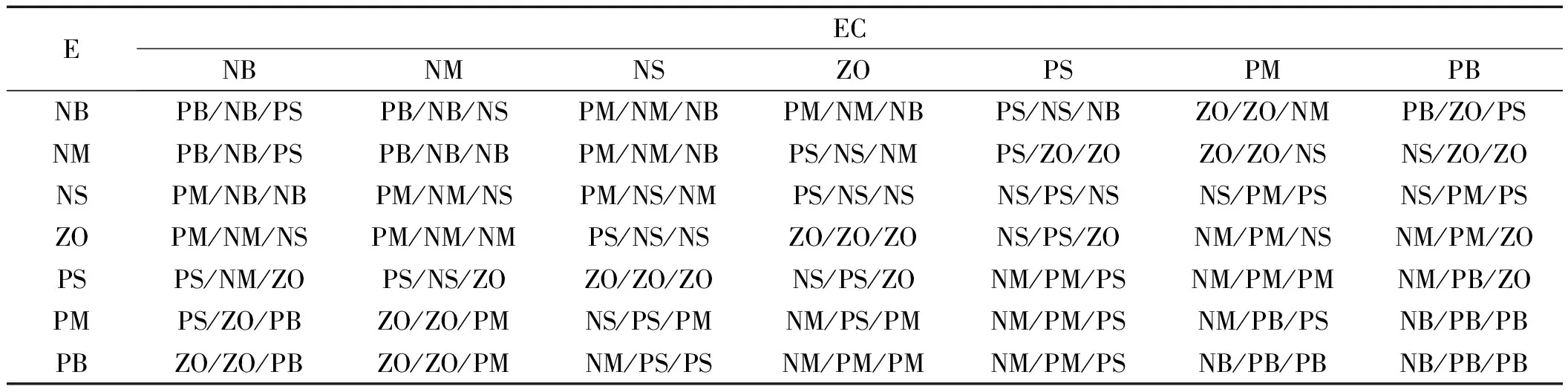
表1 ΔkP,ΔkI,ΔkD模糊规则表

3 仿真分析及实验

3.1 系统仿真模型的建立

本研究利用Matlab软件中Simulink功能模块，以及隶属度函数和模糊规则表，将已经建立好的模糊规则表嵌入到模糊控制器中，执行对象为收卷部分的伺服电机。

系统的输入信号为阶跃信号，将模糊PID的计算结果传到伺服系统，最后观察Scope的输出波形图。利用Matlab/Simulink功能模块分别建立收卷恒张力常规PID控制器的仿真模型，如图4所示。

图4 传统PID仿真模型

模糊自适应PID控制器仿真模型如图5所示。

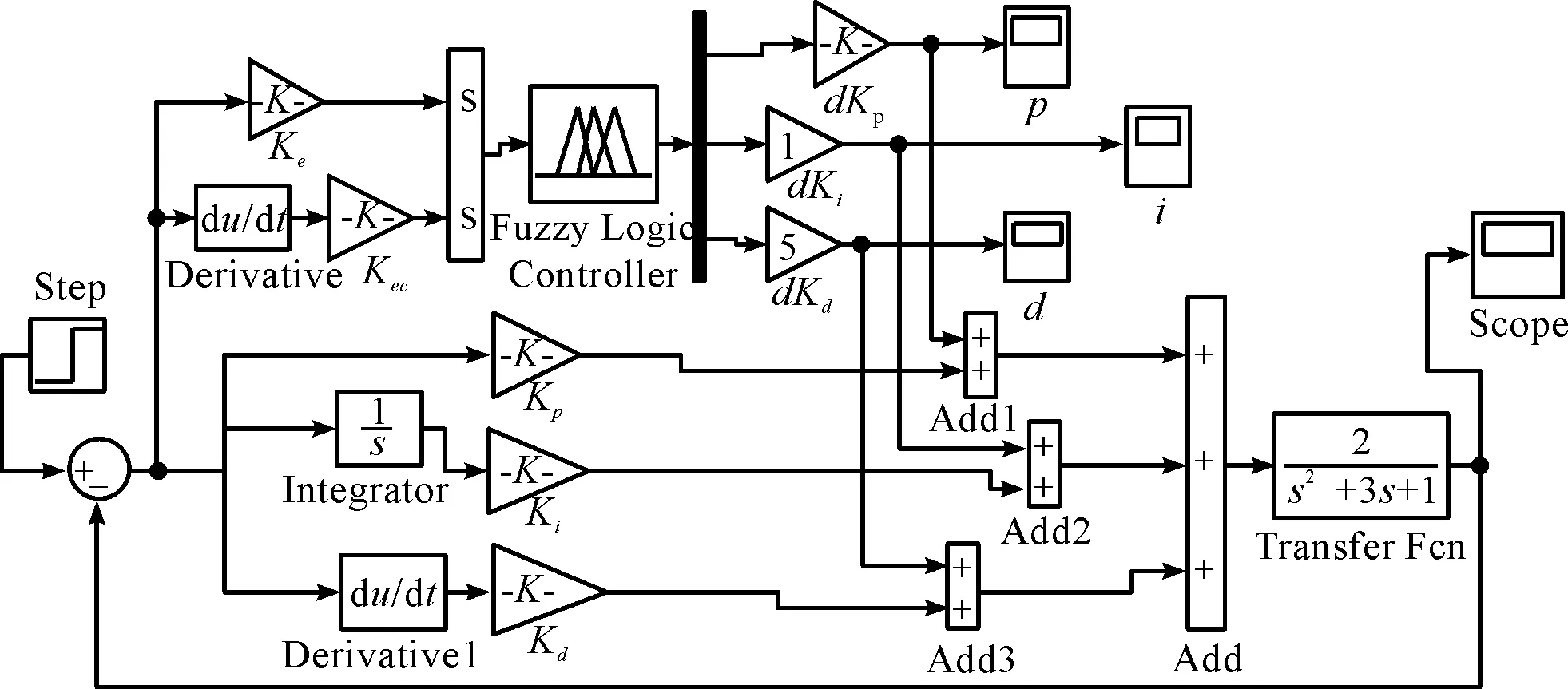
图5 模糊PID仿真模型

3.2 仿真及结果分析

常规PID与模糊PID控制系统的输出响应曲线如图6所示。

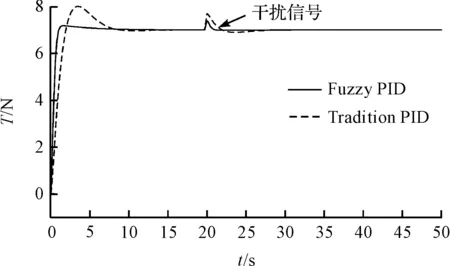
图6 控制系统抗干扰响应曲线

其中，时间为20 s处添加幅值为2的阶跃干扰信号。从图6可以看出：实际张力值围绕设定值上下波动，直至达到平衡状态。

通过实验结果分析可得到两种控制器对张力控制性能，如表2所示。

表2 两种控制算法控制对比

由表2可以看出：采用模糊PID算法，系统响应速度更快、系统超调更小，系统受到随机干扰后恢复速度更快。由于材料、系统参数设置的变化，张力系统控制对象都会产生变化，在系统时间为20 s时将张力由7 N改为9 N，以及将传递函数添加滞后环节2e-0.5/(S2+3S+1)后分别进行仿真，结果如图(7，8)所示。

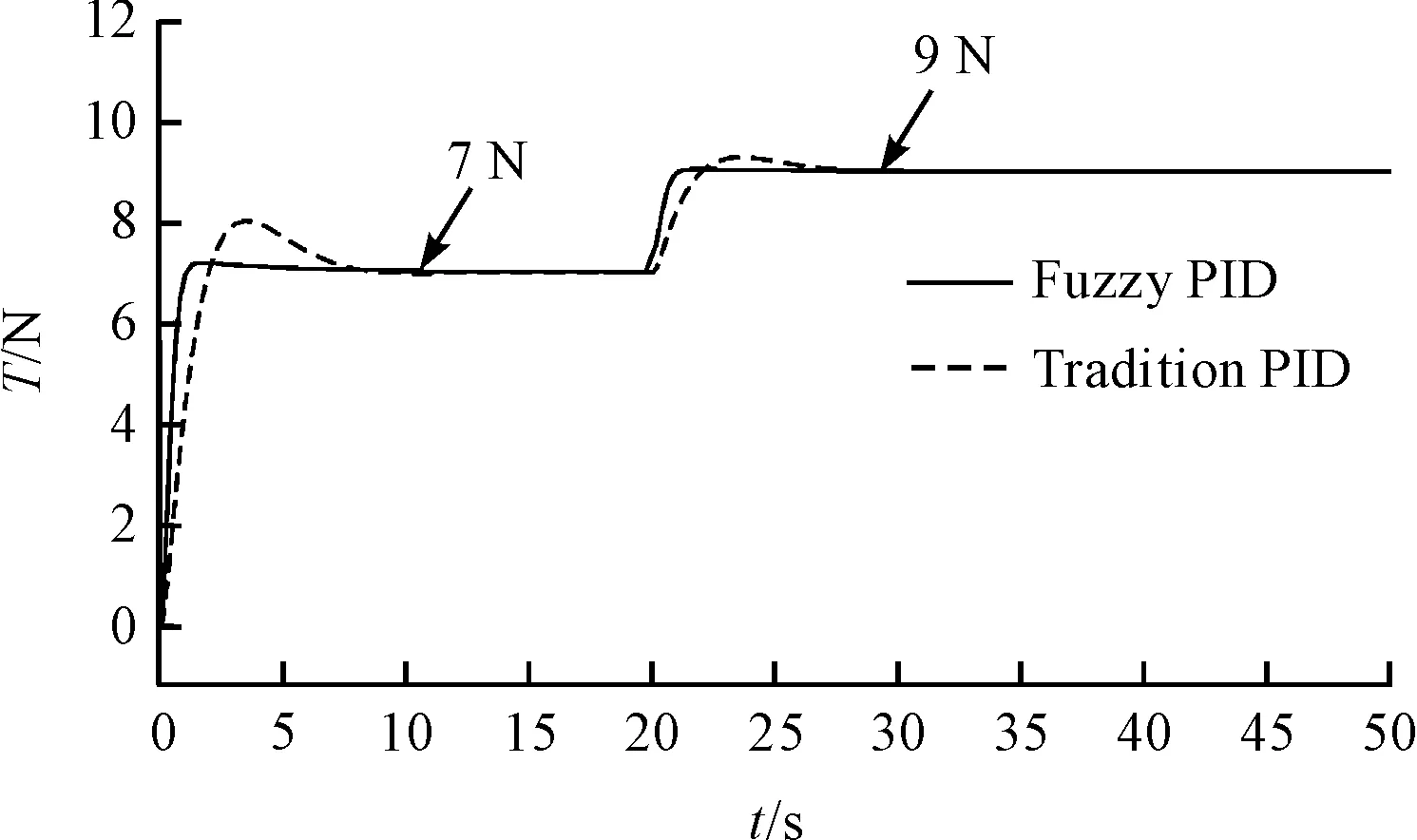
图7 控制系统参数变化响应曲线

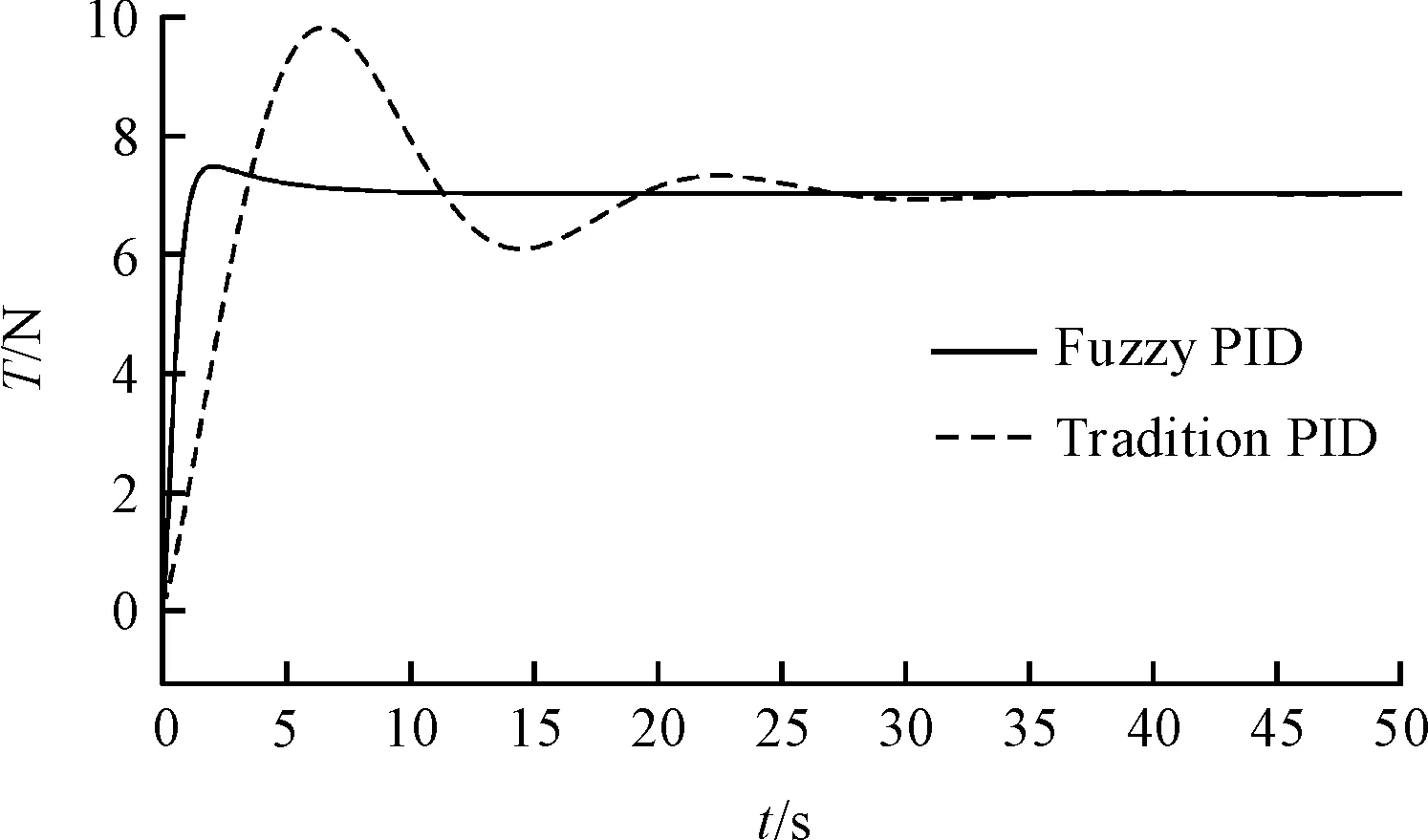
图8 添加滞后环节控制系统响应曲线

从图7可以看出：系统稳定运行过程中张力设定值更改后采用模糊PID算法控制系统恢复稳定时间更短，更平稳。

从图8可以看出：添加延时环节对采用模糊PID控制系统影响较小，而常规PID系统震荡明显，超调较大。

综上可以看出：采用模糊PID的控制系统响应速度快，稳态性较好，具有较强的鲁棒性，在系统参数变化或系统受到干扰情况下，采用模糊PID的恢复速度更快。

3.3 试验测试

本研究采用实验室的收放卷平台进行验证。卷带缠绕设备收卷部分控制结构如图9所示。

图9 收放卷平台结构

收放卷平台运行参数设置如表3所示。

表3 收放卷运行参数

系统稳定后，张力变化情况如图10所示。

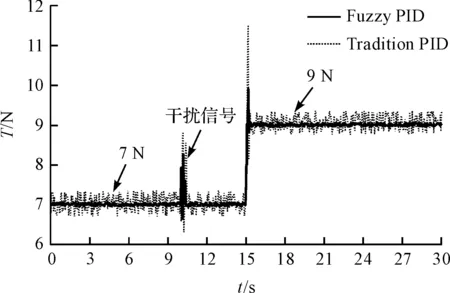
图10 稳态时段张力波动

图10可以看出:常规PID控制波动明显大于模糊PID控制。通过实验结果分析可知：模糊PID张力控制中放卷张力设定为7 N时波动率约为3%，张力设为9 N后张力波动率约为2.8%，受到人为扰动后系统快速恢复稳定。常规PID张力控制中放卷张力设为7 N时波动率约为10.2%，张力设定为9 N后张力波动率约为9.6%，受到扰动后系统快速恢复较慢，且由7 N切换到9 N过程中波动较大，过渡时间较长。由此表明，模糊PID可有效提高张力控制系统响应速度与抗干扰性，在系统参数变化后仍然具有较强的适应性，可有效实现渔网机经线张力的稳定控制。

4 结束语

针对渔网机张力的模糊PID控制，本文在常规PID控制器的基础上引入模糊控制器，克服了传统PID控制器参数不能自适应调整的缺点。从仿真及实验结果可以看出：模糊PID控制效果超调小、稳定快，在受到扰动后可以快速回到稳定状态，且张力波动范围控制在了5%以内，能够实现经线张力的稳定控制。

本研究中涉及到了3根轴的运动，对多轴的同步性考虑不足，今后本研究将通过EtherCAT现场总线控制方式来研究多轴的同步性。