ASME Ⅷ-2分析设计法在形状不规则零部件中的应用

姜红喜，李志刚，杨琼，张东海



ASME Ⅷ-2分析设计法在形状不规则零部件中的应用

姜红喜，李志刚，杨琼，张东海

（四川宏华石油设备有限公司，四川 成都 610036）

简介了ASME Ⅷ-2按分析设计法及其具体实施的等效线性化方法，并以提环强度分析为例，分别使用有限元常规分析及ASME Ⅷ-2按分析设计法进行强度计算，通过两种方法计算结论与现场试验结果的对比，可知：按照ASME Ⅷ-2对应力进行分类后，采用等效线性化方法，计算结果与实际使用情况更吻合；尤其对于形状不规则零部件，应力分类后，计算结果更符合实际工程应用；使用该方法设计计算，有利于在零部件的设计阶段，有效地把控零部件尺寸、评估影响、优化设计。

ASME Ⅷ-2分析设计方法；不规则零部件；应力分类；强度分析

在设计工作中，经常会遇到形状不规则的零部件的强度分析，使用三维有限元分析零部件强度是常用方式，但实际使用中，在材料结构整体不连续位置（如形状突变位置、开孔处等）、点线接触位置、接触面和固定位置周边等，经常会出现局部高应力的情况，此高应力不满足材料的许用应力，甚至有可能超过材料的屈服强度或抗拉强度。

在实际工程应用中，大部分采用塑性材料，出现深度很浅的小范围塑性变形不会导致零部件的失效，出现小范围塑性变形后，会引起应变强化和应力再分布，也就是说，采用常规的许用应力设计方法计算得到的局部不满足设计要求的部分，在实际工程应用中，并不会导致零部件失效。

在设计中，如果为了保证局部区域满足许用应力，采用提高材料性能或零部件尺寸的方式，会造成设计的零部件过于粗笨、空间布置受限、重量增加、生产制造成本增加等不利的后果，在这种情况下，可采用ASME Ⅷ-2中按分析设计的方法对零部件的强度进行校核。

1 ASME Ⅷ-2按分析设计方法

常用的设计方法可分为常规设计方法和分析设计方法，分析设计方法是以弹性应力分析和塑性失效准则为基础的设计方法[1]。ASME Ⅷ-2根据可能遇到的零部件应力情况，基于应力产生的原因、导出应力的方法、应力存在区域的大小及应力沿厚度的分布四项基本点出发，并针对失效模式，为了工程应用使用方便，对零部件各处的应力进行划分[2]，各应力的特征如下[3]：

（1）一次应力

①一次薄膜应力：零部件大部分区域的应力，超过屈服强度会导致零部件结构失效或产生总体变形；

②一次弯曲应力：与截面形心的距离成正比的应力，超过屈服强度会导致零部件局部区域塑性变形；

③局部一次薄膜应力：局部区域的薄膜应力，超过屈服强度会导致零部件局部区域塑性变形。

（2）二次应力

有局部屈服和小量变形发生，但一次施加这种应力不会导致失效，且再次施加应力后该部分的屈服区域不会扩展。

（3）峰值应力

不引起任何的显著变形，但可能导致疲劳裂纹或者脆性断裂。

ASME Ⅷ-2按分析设计方法对应力分类后，针对不同的应力类型采用不同的失效评判准则，如图1所示。

以下部分以顶驱提环为例，进行说明。

应力类型一次应力二次应力，薄膜应力加弯曲应力峰值应力 总体薄膜局部薄膜弯曲 说明沿实心截面的平均一次应力不包括不连续和应力集中；仅由机械载荷引起沿任意实心截面的平均应力考虑不连续但不包括应力集中；仅由机械载荷引起与离实心截面形心的距离成正比的一次应力分量。不包括不连续和应力集中；仅由机械载荷引起为满足结构连续所需的自平衡应力发生在结构的不连续处。可以由机械载荷或热膨胀差引起。不包括局部应力集中1、因应力集中（缺口）而加到一次或二次应力上去的增量；2、能引起疲劳但不引起容器形状变化的某些热应力 符号PmPLPbQF

（引自ASME Ⅷ-2图5.1）[2]

2 有限元强度分析

顶部驱动钻井在海洋和陆地多种钻机上得到广泛应用。目前国际上一些大的油气公司要求专业化服务公司的大型钻机必须配备顶驱，否则招标时可能不予考虑[4]。提环作为顶驱的重要部件，是提升系统中的主要受力构件，承载着顶驱、钻杆、钻头等井下钻具的全部重力，其力学性能直接关系到钻井工作的安全性[5]。提环形状很不规则，截面变化较大，具有几何非线性和较大的局部应力集中[6]，实际设计工作中多采用有限元分析其强度。

顶驱提环与大钩接触面为线接触，接触位置应力较大，受力后接触位置发生局部的塑性变形，变为面接触。

使用有限元分析的静强度进行校核。

2.1 材料及力学性能

提环选用材料的力学性能为屈服强度815 MPa、最小抗拉强度960 MPa。

2.2 模型处理及结果分析

提环与大钩接触面均为圆弧面，为了保证顺利安装，提环与大钩圆弧直径取值不同，提环与大钩之间线接触。

使用API 8C表6中规定的大钩最大半径1MAX＝114.3 mm[7]去接触顶驱提环，使用很小的平面模拟实际线接触情况，钩载（最大钩载4500 kN）作用在提环与大钩接触面位置。在提环销轴及销轴侧面加强圈位置施加固定约束，如图2所示。结果分析如图3所示。

图2 提环固定及加载方式

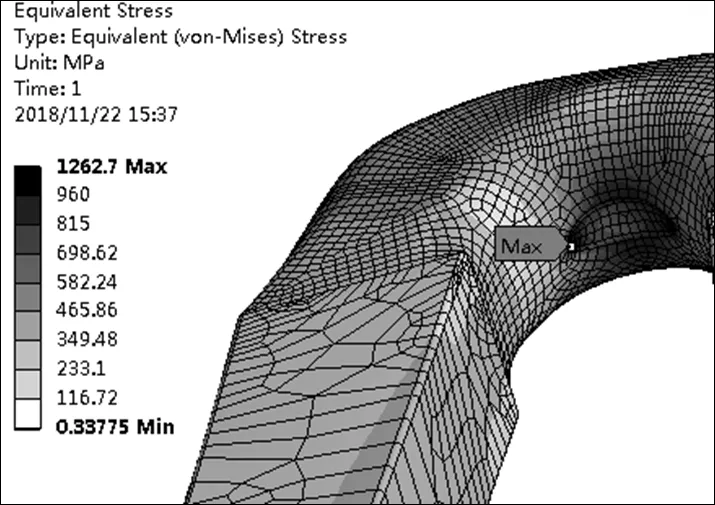
图3 静力有限元分析结果

3 许用应力法强度分析

根据API 8C，提环安全系数为2.25[7]，其许用应力＝815/2.25＝362 MPa。

从图3可看出，其最大应力为1262.7 MPa，远大于许用设计应力。但从中也可看出，最大应力主要位于接触位置边缘和接触位置，在实际工作过程中，其接触位置少量的屈服有利于应力再分配，不会造成整个提环的失效。

API 8C规范5.4节中规定，在接触区域允许有局部屈服[7]，故应用许用应力法分析，不足以判定该提环设计强度不满足要求。

4 ASME Ⅷ-2按分析设计方法强度分析

由于以上分析过程中遇到的问题，有必要对提环的应力进行分类，分类后应用ASME Ⅷ-2 按分析设计方法进行校核。

4.1 许用应力

按照ASME Ⅷ-2按分析设计方法，各类应力的许用应力如下：

＝362 MPa（按API 8C 选取）

S＝max（1.5,S）＝815 MPa

S＝max（3, 2S）＝1630 MPa

4.2 等效线性化方法

应力等效线性化概念源于ASME规范，Hollinger和Hechmer两人提出了基于应力线性化的三维应力准则[8-9]。等效线性化方法要求在结构危险截面上可能发生危险的几个部位设定一些应力线，应力线应贯穿壁厚，垂直于零件内、外两个表面或中面；然后根据合力和合力矩等效原理把沿应力线分布的应力分解成薄膜应力和弯曲应力，剩余的非线性部分则为峰值应力和二次应力，到目前为止，著名的有限元 分析程序如ANSYS、MARG、NASTRAN等都提供了应力等效线性化的后处理功能。但是，对于复杂结构，等效线性化方法存在选择应力分类线或面不唯一的困难，以及在结构不连续部位应力线性化等难点[1]。顶驱提环结构并不复杂，可以使用该方法进行应力分析。

4.3 线性化路径选取

在图3中受力较大位置选取线性化路径两条，如图4所示。

4.4 应力分类

对这两条线性化路径上的应力进行分类，得出各种类型的应力大小，如图5～图7所示。

4.5 结果分析

通过以上结果，按照ASME Ⅷ-2 按分析设计方法对其强度进行校核。

图4 线性化路径选取

图5 一次薄膜应力

图6 一次薄膜应力＋弯曲应力

图7 一次薄膜应力＋弯曲应力＋二次应力

最大钩载线性化路径1校核结果为：

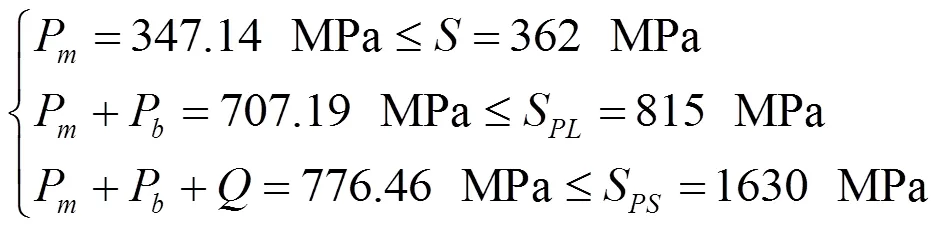
最大钩载线性化路径2校核结果为：

可知，提环绝大部分区域的应力值满足设计许用应力；小部分区域的应力值超过设计许用应力，但没有超过屈服强度，该现象主要发生在力的集中作用面上，由于作用面上产生过高的弯曲应力、局部接触膜应力引起，但并没有超过屈服强度，不会对零件的形状和受力状态产生影响；局部区域应力超过了屈服强度，由二次应力引起，发生在力作用面的边沿位置，主要是由于力施加的不连续性造成，该处有局部屈服和小变形发生，之后该部位会进行应力再分配，再次施加应力后该部分的屈服区域不会扩展，不会造成零件的失效。故该提环在最大钩载作用下，满足设计强度要求。

5 试验结果

提环按照设计图纸生产制造后，进行相关载荷试验检测，检测委托四川宏华石油设备有限公司技术检测中心进行，检测时环境温度为3℃，检测设备为IMP测量系统，检测点如图8所示，测试点①位于提环内侧、②位于固定销轴上侧截面变化位置。

1.销轴2.加载装置3.大钩4.提环5.固定装置

分别对提环施加最大工作载荷、1.5倍最大工作载荷、2倍最大工作载荷，测量各载荷下的应力值，结果如表1所示。

表1 各测量点应力值

可知：该提环载荷试验时，最大应力值为412.2 MPa，按照AIP 2C通过试验设计确认部分规定，峰值应力区的应变仪至少应为1.1的强度裕度[10]，该数值虽然超过设计许用应力362 MPa，但是测试点①为峰值应力区，仍有1.98的强度裕度，故认为满足强度要求。测试点位于前述分析中线性化路线2中2号点位置附近（图4（b）），由于该测试点没有位于力作用面的边沿位置，而是处于边沿位置附近，故二次应力的作用较小，可以参照应力分析中一次薄膜应力和弯曲应力的结果（图6（b）），其中点2附件的应力值大约为382～450 MPa，与试验结果相符。

继续加载到1.5倍最大设计载荷，可知，提环的最大应力值为620.8 MPa，仍然在屈服强度的范围之内，并没有发生屈服；继续加载2倍最大工作载荷后，提环的最大应力值为826.7 MPa，大于最小屈服强度，发生局部屈服，但远小于最小抗拉强度960 MPa，不会有裂纹产生，且加载到2倍最大工作载荷卸载后，提环无肉眼可见的变形，探伤也未发现裂纹。强度和变形均满足要求。

使用常规分析方法，在加载到4500 kN时，最大应力为1262.7 MPa，超过最小抗拉强度960 MPa，会有裂纹产生，而实际试验过程中，在加载到9000 kN后，提环强度仍满足要求，无裂纹产生。使用应力分类方法后，试验结果与应力分类计算结果基本吻合。

6 结论

通过以上有限元分析中应力不分类与分类的计算结果对比，可以看出，单纯采用许用应力设计方法、应力不分类的情况下，计算强度不满足设计要求，ASME Ⅷ-2按分析设计方法对应力进行分类后，计算强度满足设计要求；通过载荷试验验证，其强度满足设计要求，可见应力分类后结果更合理，更适用于工程应用。

故对于提环等形状不规则的零部件，使用ASME Ⅷ-2按分析设计方法对应力进行分类后，进行强度校核，可以在设计阶段有效地把控零部件尺寸，确认有限元分析中超过许用应力部分对于零件失效的影响，从而优化设计；避免设计的零部件过于粗笨、重量增加、生产制造成本增加等不利后果。

[1]周羽，包士毅，董建令，等. 压力容器分析设计方法进展[J]. 清华大学学报（自然科学版），2006，46（6）：886-892.

[2]ASME BPVC.VIII.2-2015，ASME Ⅷ-2 ASME Boiler & Pressure Vessel Code – Rules For Construction Of Pressure Vessels [S]. 2015.

[3]丁伯民. ASME Ⅷ压力容器规范分析[M]. 北京：化学工业出版社，2014：282-284.

[4]李传华，杨启伟. 顶驱钻机技术进展及建议[J]. 河南石油，2005，19（5）：49-51.

[5]蒋波，赵毅红，王军领，等. 基于ANSYS的提环有限元分析及优化[J]. 扬州大学学报（自然科学版），2011，14（4）：60-63.

[6]冯庆东，张林海，侯宇，等. XSL675型旋扣水龙头提环有限元分析[J]. 石油矿场机械，2016，45（1）：46-50.

[7]API 8C-2012，Drilling And Production Hoisting Equipment[S]. 2012.

[8]Hollinger G L，Hechmer J L. Three-dimensional stress criteria-A weak link in vessel design and analysis [J]. ASME Pressure Vessel and Piping，1986（109）：9-14.

[9]Hollinger G L，Hechmer J L. Summary of example problems from PV RC project on three dimensional stress criteria [J]. ASME Pressure Vessel and Piping，1996（338）：19-24.

[10]API 2C-2012，Offshore Pedestal-mounted Crane[S]. 2012.

ASME Ⅷ-2 Application in Irregular Shape Parts and Components

JIANG Hongxi，LI Zhigang，YANG Qiong，ZHANG Donghai

( Sichuan Honghua Petroleum Equipment Co., Ltd., Chengdu 610036, China )

Introduce the stress classification analysis in ASME Ⅷ-2 alternative rules and its application – equivalent linearization method. Using the strength analysis of bail as example，considered the strength with the routine element analysis and stress classification analysis in ASME Ⅷ-2 alternative rules, then compared the two different analysis results with the results of factory experiment, found that after classifying stress as ASME Ⅷ-2 alternative rules, using the equivalent linearization method, the stress calculation result is more in line with actual usage, especially for the irregular shape parts and components, the analysis results is more suitable for engineering application; Using the stress classification analysis and the equivalent linearization method is good for designing the irregular shape parts and components, we can control the size of parts and components effectively, assess impact and optimize design.

ASME Ⅷ-2 alternative rules；irregular shape parts and components；stress classification；strength analysis

TH123+.3

A

10.3969/j.issn.1006-0316.2018.12.010

1006－0316 (2018) 12－0033－06

2018－05－25

姜红喜（1984－），女，甘肃平凉人，硕士，工程师，主要从事石油机械设备设计研发工作。