基于模糊自整定粒子群算法的多圆盘过滤机槽体液位控制系统

汤 伟 佟永亮 王 帅 袁志敏 宋 涛

(1.陕西科技大学电气与信息工程学院，陕西西安，710021; 2.陕西农产品加工技术研究院，陕西西安，710021; 3.安德里茨(中国)有限公司，广东佛山，528000)

纸机抄造过程中排出的白水中含有大量的纤维、填料等物质，将其直接排放不仅会造成浪费，还会污染环境。对于白水的处理一般采用多圆盘过滤机进行回收。在白水回收过程中，多圆盘过滤机槽体液位直接影响白水回收效率。当前对于过滤机槽体液位控制在稳定进浆流量的基础上，通过调节过滤机中心主轴转速来实现液位控制，但槽体液位控制系统存在非线性、时滞的特点，同时由于液位存在波动，使得液位检测值存在波动，增加了过滤机液位控制的难度，寻求合理的多圆盘过滤机槽体液位控制算法成为解决槽体液位控制的重要方法。

当前对于多圆盘过滤机液位控制多采用传统的比例积分微分(Proportional Integral and Derivatice， PID)控制。PID控制具有结构简单、不依赖对象模型、且具有令人满意的控制性能和良好的鲁棒性[1]，但PID控制器的控制效果依赖于PID参数，故PID参数整定显得尤为重要。目前其主要的整定方法有两类：①传统参数整定方法，如ZN法、单纯形法、幅值裕度法等；②智能化整定方法，如基于遗传算法[2]、蚁群算法[3]、粒子群算法[4]等智能PID优化方法。粒子群优化(Particle Swarm Optimization， PSO)算法作为一种高效、简单的并行搜索算法，具有程序易实现、参数调整少、鲁棒性好等优点，但将其应用于PID参数整定时，算法后期易出现早熟问题，计算精度低、收敛速度慢。因此，本课题提出了一种模糊自整定粒子群优化(Fuzzy Self-Tuning Particle Swarm Optimization， FST-PSO)算法来整定多圆盘过滤机槽体液位控制回路的PID参数，MATLAB/Simulink仿真结果与实际应用过程表明，经FST-PSO算法优化后的PID控制提高了槽体液位控制的精度，降低了液位的波动，提高了白水回收效率。

1 槽体液位控制系统

1.1 多圆盘过滤机白水回收工艺

原白水与垫层浆被泵送至多圆盘过滤机的进料箱内，混合后白水溢流至过滤机槽体。在主轴电机的作用下，中心主轴带动过滤圆盘旋转，在水腿产生的真空抽吸力的作用下，槽体内白水流入滤盘内部、纤维附着在过滤圆盘表面形成滤饼，随滤盘旋转，滤盘表面滤饼厚度增加，过滤阻力变大，白水中纤维通过量逐渐减少，所以通过过滤圆盘后的滤液中固形物含量逐渐降低，便形成了固形物含量不同的3种滤液：浊滤液、清滤液、超清滤液(清滤液和超清滤液均来自于真空过滤区)。随着过滤的进行，滤盘表面沉积的滤饼在剥浆水流作用下被剥除，继而进入下一个过滤周期[5- 7]。多圆盘过滤机滤盘盘面分区图如图1所示。

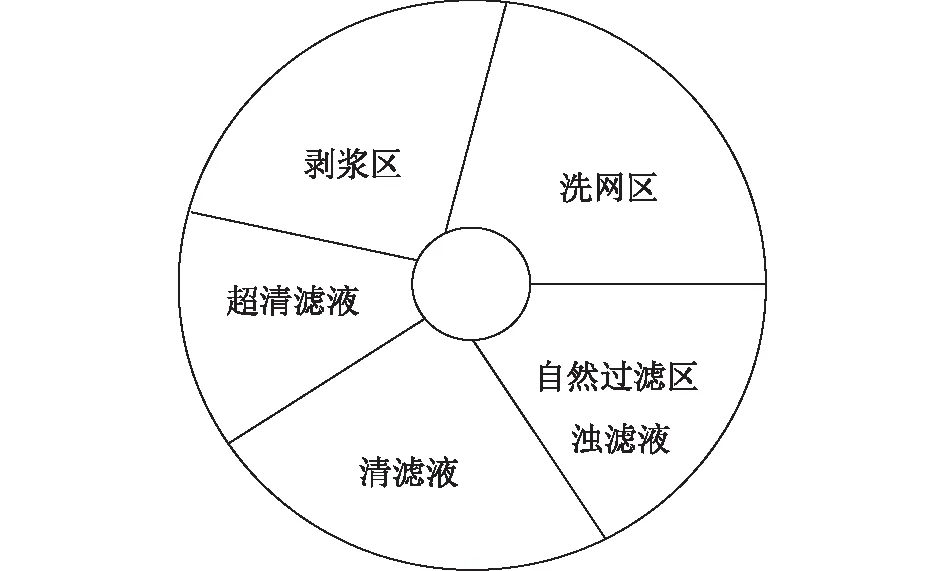
图1 多圆盘过滤机滤盘盘面分区图

1.2 槽体液位对白水回收效率影响

白水处理过程中，槽体液位直接影响白水回收效率。当液位低于滤盘中心主轴时，滤盘便不会形成真空，过滤机不能正常工作；当液位高于中心主轴时，随着液位的增加，其白水处理能力增强，但是液位过高时，也会降低白水回收效率。液位过高时，滤饼出液面后就被剥浆水流剥下，减少了出液面后的真空过滤区运行时间在整个过滤周期内的比例，相应地会减少超清滤液的形成，降低白水回收效率；同时，在同等浓度下，液位高度增加时，滤盘表面沉积的纤维量增加，滤饼厚度增加，但是脱水时间短，此时滤盘表面的纤维含水量大，不易形成浆层，便不易被剥浆水流剥下，纤维附着在滤盘表面，影响滤网的再生能力，降低白水回收效率[8]。当液位高于接浆斗时，会造成混合后白水直接通过回收浆料通道流走，过滤机不能正常工作。综合回收效率和处理能力，当前多圆盘过滤机槽体内液位设定为高于中心主轴100～200 mm[9]。

1.3 槽体液位控制回路

在流量控制回路的作用下，槽体内混合后白水的流入量稳定在一定范围内，进而通过液位控制回路实现槽体液位的控制，其控制回路如图2所示。液位传感器检测到液位的实际值，通过实际值与设定值运算获得偏差，偏差传输至控制器调节主轴电机的频率，通过主轴转速的不同来调节滤液流出量进而调节液位。当主轴电机频率增大时，主轴转速增加，单位时间内滤液的流出量增加，液位降低；同理，主轴电机频率减小，主轴转速减小，单位时间内滤液的流出量降低，液位升高。

图2 多圆盘过滤机槽体液位控制回路图

2 粒子群算法及其改进

2.1 标准粒子群算法

PSO算法是Kennedy和Eberhart根据鸟类捕食行为发明的一种全局优化算法[10]。算法在d维空间中存在m个粒子，则粒子i(i=1，2…m)第t次迭代后，当前位置为xi(t)=[xi1，xi2，…xid]，当前速度为vi(t)=[vi1，vi2，…vid]。设pbesti(t)=[pi1，pi2，…pmd]为粒子i所经历的最好位置，gbest(t)为群体所经历的最好位置。粒子根据自身当前的速度和位置进行迭代，则第(t+1)次的迭代公式见公式(1)和公式(2)。

vi(t+1)=wvi(t)+c1r1(pbesti(t)-xi(t))+c2r2(gbest(t)-xi(t))

(1)

xi(t+1)=xi(t)+vi(t+1)

(2)

式中，ω为惯性权重，ω的取值范围为(0.4，1)[11]；r1、r2是在[0，1]之间均匀分布的随机数；c1为认知因子，c2为社会因子，c1和c2被统称为学习因子，c1、c2的取值范围为(0.5，2.5)[12]。为了迭代过程中避免粒子冲出搜索空间，一般限定粒子位置的取值范围为[xmin，xmax]，以此对粒子的移动范围进行限制，达到对算法更好的控制。

2.2 模糊自整定粒子群算法

标准PSO算法中，惯性权重ω决定了粒子对当前速度继承的多少，较大的ω具有较强的全局搜索能力，反之，较小的ω有较强的局部探索能力[13]；c1、c2分别表征了粒子个体的最优位置的重要性和全局最优位置的重要性，在运算过程动态的调整c1、c2的大小可以产生良好的计算结果[14]。基于此，本课题提出一种依据粒子的迭代系数、粒子相似度、粒子适应度误差3个参数，利用模糊控制动态调整粒子群算法的惯性权重ω、学习因子c1、c2的方法，平衡PSO算法的全局搜索能力和局部探索能力，从而有效地解决粒子群早熟和收敛速度慢问题。

2.2.1 模糊控制器输入变量的定义

(1)迭代系数

粒子的迭代系数是群体中个体当前迭代次数与最大迭代次数的比值，以此来衡量迭代进程。在算法初期，λ趋近于0，随迭代的进行，λ逐渐趋近于1，即λ∈(0，1)，其计算见公式(3)。

(3)

式中，t表示当前的迭代次数，maxiter表示最大迭代次数。

(2)粒子相似度

粒子的相似度是所有粒子与全局最优粒子的空间距离的平均值开平方的倒数。当粒子与最优粒子的相距很远时，那么粒子与全局最优粒子距离的平均值就会变大，粒子的相似度就会很小，γ趋近于0；同理，空间距离小时，其相似度相应的就会增强，γ趋近于1，即γ∈(0，1)，其计算见公式(4)。

(4)

式中，m为种群中粒子总数，d表示所求问题的维数，xij(t-1)表示上一迭代时第i个粒子的第j维的位置，gbestj(t-1)表示截止上一次迭代的全局最优粒子的第j维。

(3)适应度误差

粒子的适应度误差是全局最优粒子的适应度值与所有粒子适应度值比值的平均值与1之间的误差。当粒子的收敛效果不好时，全局最优粒子适应度值与粒子的适应度值之比较小，相应的误差会大，ε趋近于1；当趋近于全局最优时，全局最优粒子适应度值与粒子适应度值之比变大，趋近于1，则误差ε趋近于0。即ε∈(0，1)，其计算如公式(5)所示。

(5)

式中，f_gbest为粒子的全局最优粒子的适应度值，fit(i)为第i个粒子的适应度值。

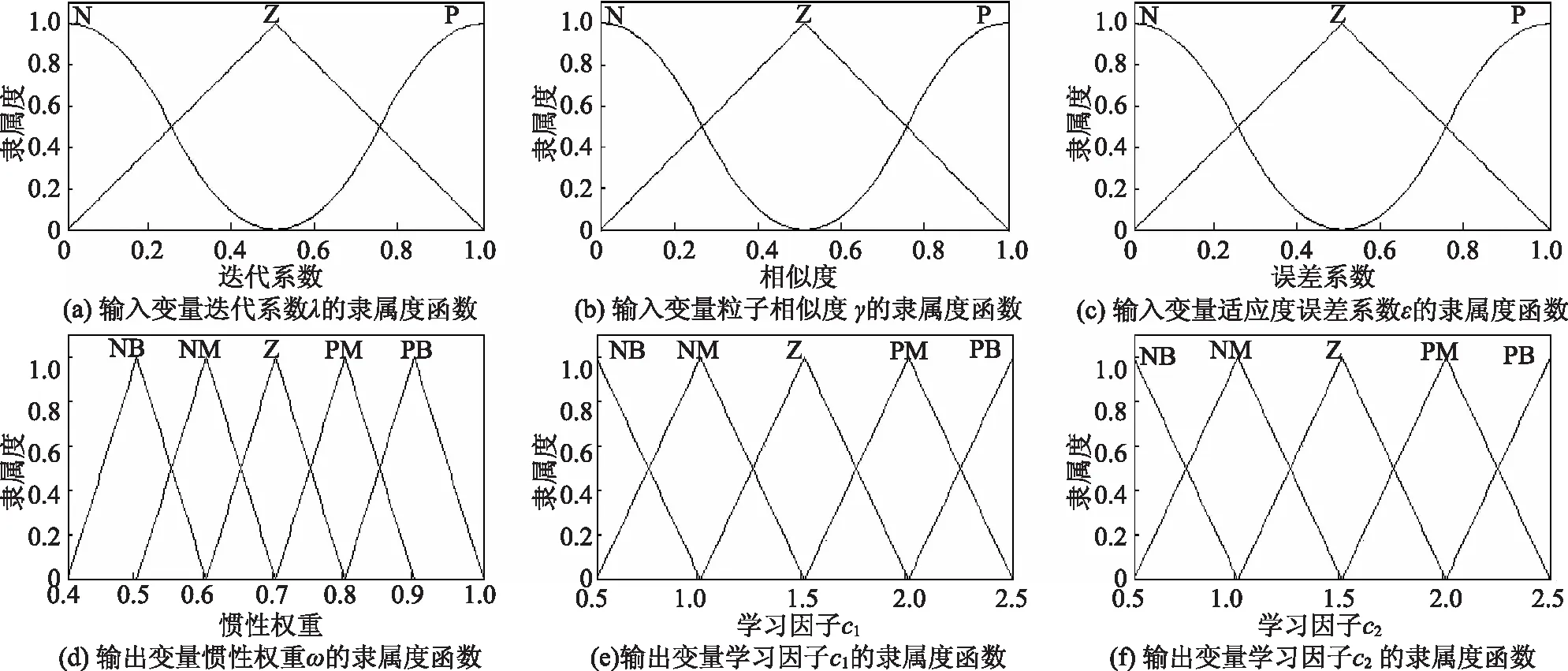
图3 模糊控制器输入变量、输出变量隶属度函数

2.2.2 模糊控制器设计

该模糊控制器的输入为迭代系数λ、粒子相似度γ、粒子适应度误差系数ε，输出惯性权重系数ω，学习因子c1、c2。由以上分析知，λ、γ、ε的设定论域为[0，1]，分为“负(N)”、“零(Z)”和“正(P)”；惯性权重系数ω的设定论域为[0.4，1]，分为“负大(NB)”、“负中(NM)”、 “零(Z)”、“正中(PM)”和“正大(PB)”；学习因子c1、c2的设定论域为[0.5，2.5]，分为“负大(NB)”、“负中(NM)”、 “零(Z)”、“正中(PM)”和“正大(PB)”。输入变量和输出变量的隶属函数如图3所示。模糊控制器的模糊推理选择Mamdani推理法[15]，解模糊选择centroid重心法。

应用模糊控制来动态调整粒子群的参数是为了能够平衡粒子群运算初期的全局搜索能力和后期的局部探索能力，避免粒子产生早熟，提高收敛速度。同理，当相似度高、适应度误差小时，粒子距离近，应当增加粒子的全局搜索能力，避免进入局部最优；反之，当相似度低、适应度误差高时，应增强粒子的局部探索能力[16]。根据以上原则，制定模糊推理规则如表1所示。

FST-PSO算法的流程框图如图4所示。

3 FST-PSO算法优化PID控制器参数

3.1 槽体液位控制系统

槽体液位控制结构框图如图5所示。其中r(t)为液位设定值，y(t)为液位的实际检测值，e(t)为液位的设定值与检测值之差，kp、ki、kd分别为时间、积分、微分常数，u(t)为控制器输出值。

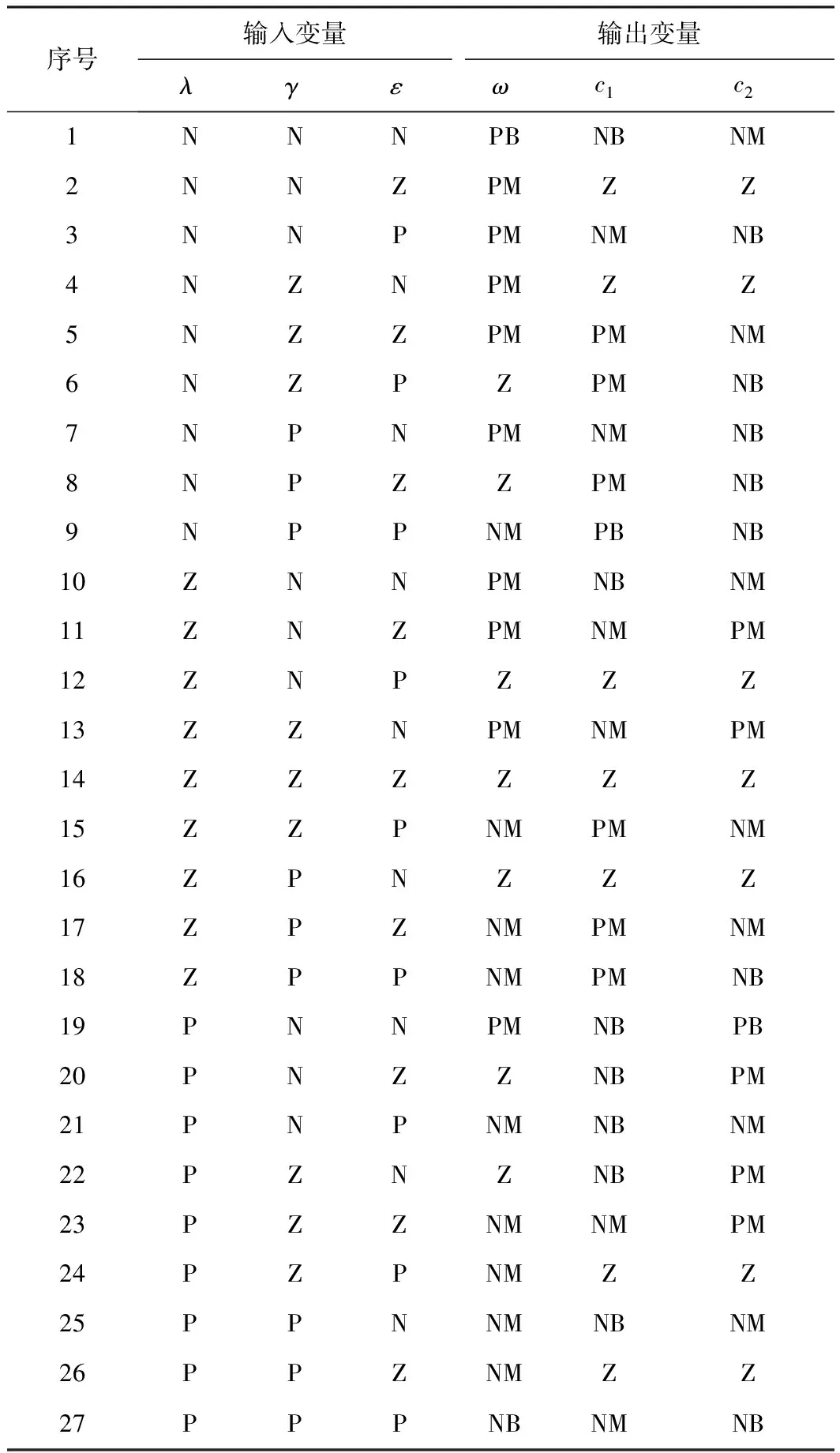
表1 FST-PSO模糊逻辑规则表

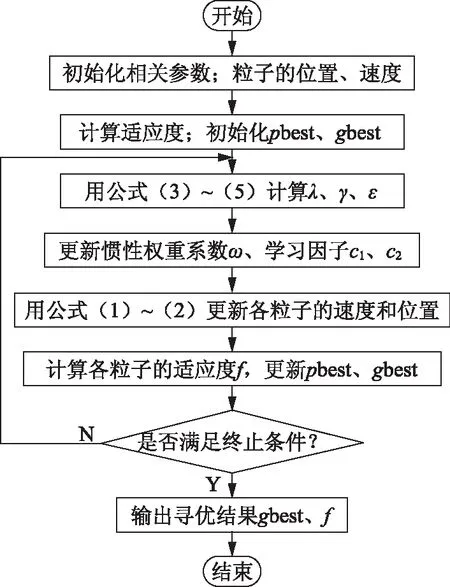
图4 FST-PSO算法流程框图

图5 基于FST-PSO算法的PID控制系统框图

(6)

3.2 基于FST-PSO算法的PID控制器参数优化

PID在槽体液位控制过程中，并不能表现出良好的控制性能，并不是PID不适用于该过程，只是PID参数不能够满足要求。针对上述问题，利用FST-PSO算法的寻优能力，在参数限定的范围内找出一组使控制性能指标最优的PID参数，其控制器原理如图5所示。PID控制器的传递函数形式表达见公式(7)。

(7)

选取适应度函数f(x)的关键在于使优化后控制系统的偏差信号e(t)趋于零，并且具有较快的响应速度和较小的超调量，因此常采用能体现综合性能的指标。绝对偏差积分(IAE)、时间偏差平方积分(ITSE)、积分平方偏差(ISE)、时间绝对偏差积分(ITAE)为常用的综合性能评价指标。结合实际和各指标差异，本课题选取ITAE为适应度函数(目标函数)，其表达式见公式(8)。

(8)

根据FST-PSO算法流程，应用PID参数优化问题时，首先描述粒子特征的维数d=3；然后初始化粒子的速度和位置，粒子位置的初始化按照ZN-PID的方法进行初始值区间的初步确定；最大限制速度为位置范围之差的一半，而后根据算法流程进行PID参数优化。

4 系统仿真及应用

4.1 实验仿真分析

基于MATLAB/Simulink平台，运用ZN经验法(ZN-PID)、标准PSO算法(STD-PSO-PID)及本课题所提FST-PSO算法整定PID参数(FST-PSO-PID)对多圆盘过滤机槽体液位控制回路进行PID参数调节，被控过程传递函数如图6所示。

图6为标准PSO、FST-PSO优化对象Gp(s)的优化过程曲线。由图6可知，FST-PSO算法与标准PSO算法相比有效地避免了早熟现象，提高了收敛速度和精度。

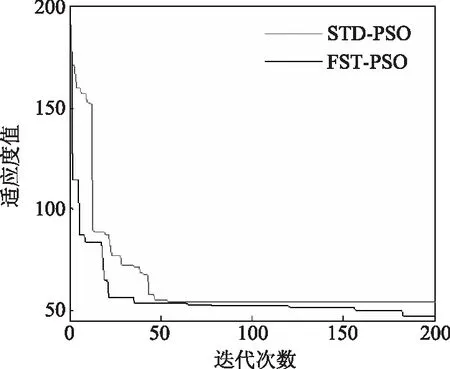
图6 PID控制器参数优化过程曲线

经以上3种方法整定优化后得到PID控制器参数如表2，控制效果见图7。图7(a)为标称对象Gp(s)在不同算法整定优化下的单位阶跃响应和负载扰动响应曲线；图7(b)为对象Gp(s)的时间常数T增大30%时的单位阶跃响应曲线和负载扰动响应曲线；图7(c)为对象Gp(s)的纯滞后时间常数τ增大30%时的单位阶跃响应曲线和负载扰动响应曲线；图7(d)为对象Gp(s)的时间常数T、纯滞后时间常数τ同时增大30%时的单位阶跃响应曲线和负载扰动响应曲线。

图7 不同被控对象的动态响应曲线

在以上各图中，负载扰动在t=100 s时加入，扰动大小为20%的单位阶跃信号。

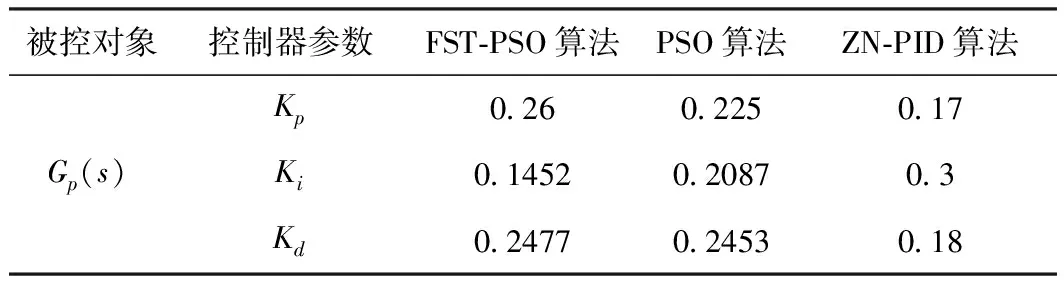
表2 PID控制器的整定优化参数

由图7的动态响应曲线可以看出，相比于ZN经验法整定的PID，经过FST-PSO算法优化的PID参数在被控对象处于标称情况下时，超调量小，调节时间短，响应速度快；当参数发生摄动时，其优化的PID参数相比于ZN-PID在调节时间、响应速度以及鲁棒性方面依旧存在较大的优势。相比于标准PSO算法优化的PID参数，经过FST-PSO算法优化的PID参数在被控对象的响应速度和鲁棒性上两者差距不大，但是无论被控对象处于标称情况还是受到摄动时，经过FST-PSO算法优化的PID参数的超调均小于经标准PSO算法整定的PID参数。综合控制器的响应速度、调节时间、鲁棒性能、超调量等性能，相比于ZN经验法整定的PID、标准PSO算法优化的PID参数，经过FST-PSO算法优化的PID参数表现出良好的控制性能。

4.2 实际应用

本课题所述控制算法已应用于保定满城某造纸厂多圆盘过滤机槽体液位控制回路中。该厂多圆盘过滤机液位最高限为2 m，经过量程标定将液位高度转化为0～100%。该厂将液位的设定值设置在高于中心主轴顶点160 mm，经标定后为88%。应用常规PID控制，液位总是出现大超调、响应时间长、控制精度低等问题，液位的实际检测值为84%～94%，控制精度为6.82%。液位在1680～1880 mm之间波动，高于中心主轴80～280 mm之间，不满足工艺要求在主轴上方100～200 mm的范围内，影响多圆盘过滤机白水回收效率。针对这一问题，应用FST-PSO算法进行多圆盘过滤机槽体液位控制。结合OPC技术，读取PLC中的信号送入MATLAB工作空间，经过MATLAB中的基于FST-PSO算法的PID控制器参数整定，然后将结果通过OPC协议送回到PLC，通过AI模块输出主轴电机变频器频率，通过调节中心主轴转速调节槽体液位，实现槽体液位控制。经过现场调试，在工况稳定后，得到某一时间段的浓度监控画面如图8所示，在保证设定值88%不变的情况下，液位的实际检测值为86%～90%，控制精度为2.27%。液位在1720～1800 mm之间波动，高于中心主轴120～200 mm之间，满足工艺需求，提高了液位控制精度和白水回收效果。证明该算法具有一定实际价值。

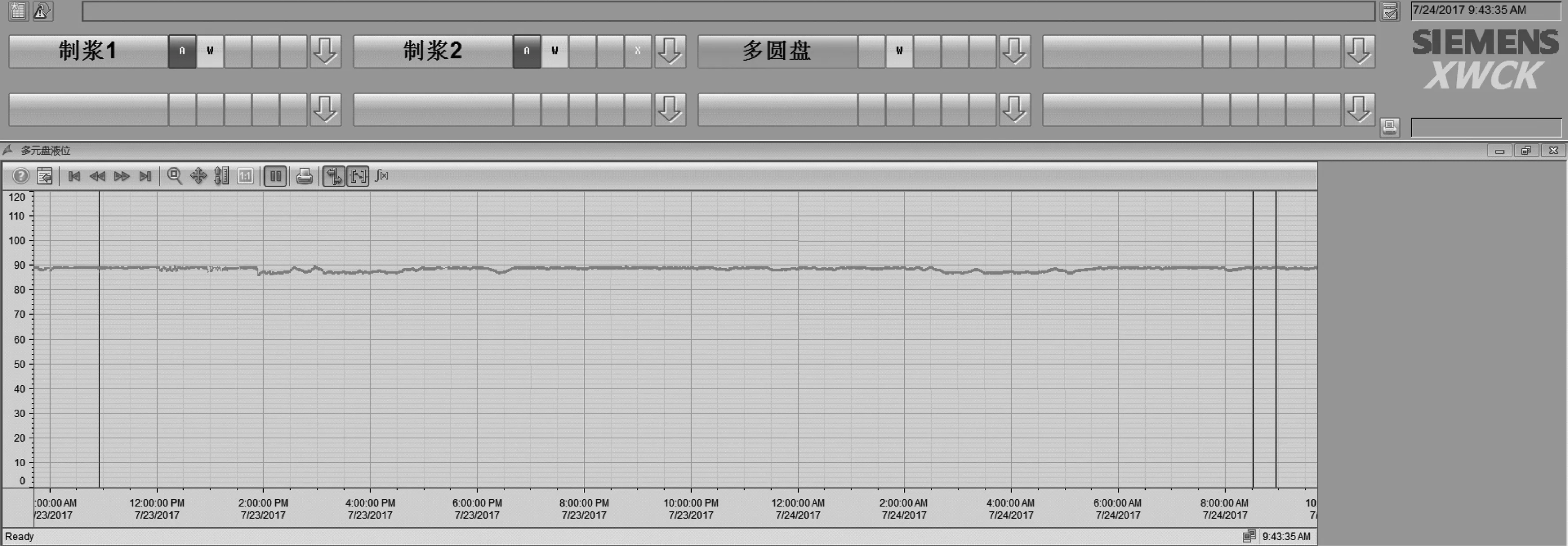
图8 多圆盘过滤机槽体液位控制系统实时运行曲线

5 结 语

本课题将模糊自整定(FST)与PSO算法相结合提出了一种FST-PSO算法，并将该算法用于多圆盘过滤机槽体液位控制回路PID控制器参数优化。仿真实验结果表明，本课题提出的FST-PSO算法有效地避免了标准PSO算法陷入早熟问题，提高了算法的收敛精度，证实了算法的有效性。相较于常规PID控制、STD-PSO算法控制，FST-PSO算法具有超调量小、响应速度快、鲁棒性强的优点。在实际应用中，槽体液位控制精度高、偏差较小，实现了算法收敛与工程需求的结合。