基于CFD低浓盘磨机浆料流动的数值模拟研究

石 宇 卢晓江 杨建伟

(天津科技大学机械工程学院，天津，300222)

盘磨机是最主要的磨/打浆设备，耗电量约占制浆造纸企业能耗的30%[1]。深入研究盘磨机节能技术对制浆造纸行业节能降耗、减少污染具有重要的意义。

磨浆是在封闭的空间内进行，浆料的流动、剪切挤压是一个十分复杂的过程。一方面是因为难以实验观察，另一方面是实验成本较高。计算流体动力学(Computational Fluid Dynamics，CFD)模拟不但可以降低实验周期和成本，而且可以突破实验条件的限制，获得磨浆区域浆料流动信息，如磨片压力、剪切力、扭矩、速度场、压力场等通过实验很难获得或者无法获得的数据。同时，网格生成、湍流模型等各个方面的不断完善，使CFD数值模拟表现出越来越多的优越性[2]。

2007年，芬兰学者Huhtanen J P[3]采用CFD和统计学的混合模拟方法对圆柱形磨浆机的磨浆过程进行了模拟。结果表明，该方法可以用于磨浆机效能和磨浆强度的研究，通过分析可以建立磨片参数、磨浆机操作参数和浆料质量参数之间的联系，在保证磨浆质量前提下为降低能耗提供了可能。2009年，波兰学者Kondora G等人[4- 6]采用FLUENT软件对简单齿纹盘磨机的磨浆过程进行了CFD建模研究。假定浆料为单相牛顿和非牛顿流体，讨论了浆料浓度变化对流体黏度变化的影响。2014年，王佳辉等人[7]对盘磨机进行了计算机模拟磨浆过程，分析了齿槽内的浆料流动状况。2016年，韩鲁冰等人[8]采用局部和宏观相结合的方式分析了盘磨机磨浆过程的趋势。2017年，刘欢等人[9]综述了盘磨机纸浆流动的最新进展。

在模拟磨浆过程方面，以往的磨齿研究模型大多都简化为部分齿，以局部分析为主，只能分析槽与槽之间的浆料流动状况，具有一定的片面性。而把整个磨浆区作为模拟对象，能够分析整个磨浆区的流动状况和压力分布状况，为整体设计优化齿纹提供依据，这些是无法在部分磨齿分析中得到的。基于此，本课题将整体模型作为分析对象，对磨浆区的整体压力分布，动、定磨盘的槽内纸浆流动状况和应力分布状况等进行分析，从而为磨片的设计优化提供思路。

1 基本假设与盘磨机结构建模

CFD的理论基础包括质量守恒、动量守恒和能量守恒三大定律，由它们可以分别导出质量守恒方程、动量守恒方程和能量守恒方程。CFD就是建立在纳维-斯托克斯方程(N-S)的基础上利用计算机进行求解。本课题计算机模拟的研究对象是低浓盘磨浆。

1.1 基本假设

假设浆料连续、定量地进入磨区，并且布满整个磨区，磨盘间不存在接触作用，间隙一致。磨盘转速和压力恒定，整个磨区内黏度一致。假定盘磨机内浆料为单相均匀牛顿流体，浆料的密度、黏度根据实测确定，由于转盘高速旋转，浆料受到剪切力作用，在磨室内部处于湍流状态，所以选择湍流方程k-ε模型进行求解，k-ε模型假定湍流为各向同性的均匀湍流。

1.2 模型建立和网格划分

利用SolidWorks软件建立盘磨机模型。动磨盘的磨片直径为300 mm，动磨盘的齿宽和槽宽均为4 mm，齿高为5 mm，齿倾角为10°，动磨盘中间加入拨料器，在动磨盘的边缘采用3个凸出坝促进浆料离开浆料室。定磨盘的磨片直径为300 mm，中间开口直径为80 mm，作为浆料的入料处，磨齿的参数和动磨盘的相同。浆料出口直径为68 mm。动磨盘、定磨盘和磨区的三维模型如图1所示。

采用ABAQUS软件对磨浆全流场计算模型进行网格划分，由于模型比较复杂，网格划分采用三角形划分和自由网格划分的方法，流体和实体模型的网格尺寸为5 mm。浆料的网格数量为12138个，定磨盘的网格为99268个，动磨盘的网格为73068个。划分后的网格图如图2所示。

图2 网格划分图

1.3 边界条件的设定

边界条件设定包括压力设定、黏度和密度的设定。计算机模拟涉及到的参数有:浆料的属性(包括密度和黏度)，工艺参数(包括磨浆间隙、磨片转速、磨片参数、进料压力、出口压力)，磨片的属性等。磨片的材料采用不锈钢，其属性为：密度7850 kg/m3、杨氏模量2.1×1011Pa、泊松比0.3。浆料密度为1050 kg/m3(浓度为5%)、黏度为4.5 Pa·s，浆料进口压力为0.3 MPa，出口压力为0 MPa。

本课题流体采用湍流计算的方式，分析时间为0.2 s，最小分析步采用0.001 s。入口采用压力入口，压力值为0.3 MPa，进口端湍流的动能K值为1×10-5，湍流动能耗散率ε为10%，出口压力值为0 MPa。耦合接触面为不滑动，实体部分采用显示动力学分析，分析时间为0.2 s，定磨盘采用全固定的方式，动磨盘加载速度1000 r/min。综合以上数据得出相关参数如表1所示。

图1 动磨盘、定磨盘和磨区的三维图

湍流模型k-ε流体密度/kg·m-31050流体黏度/Pa·s4.5边界入口压力/MPa0.3边界出口压力/MPa0转子转速/r·min-11000

2 模拟结果与分析

2.1 磨浆过程压力分析

图3所示为磨浆过程压力图。其磨浆机间隙为0.5 mm(其他不同磨浆间隙情况类似)，模拟时间为0.2 s。从图3可以看出，模拟时间为0时，入口端压力最大，出口端压力最小；在入口端到出口端的方向上，压力逐渐减小；且离入口端较近和离出口端较远的地方压力比较大，因为离出口较远，压力得不到释放；随着时间的推进，模拟时间为0.2 s时，压力比较大的区域逐渐变化，最后的结果显示最大压力分布在磨浆区的磨片上，在磨片径向大概1/3处(靠近入口端)，压力最大，比入口端和出口端都大，这会导致浆料在通过此区域时流通不畅。

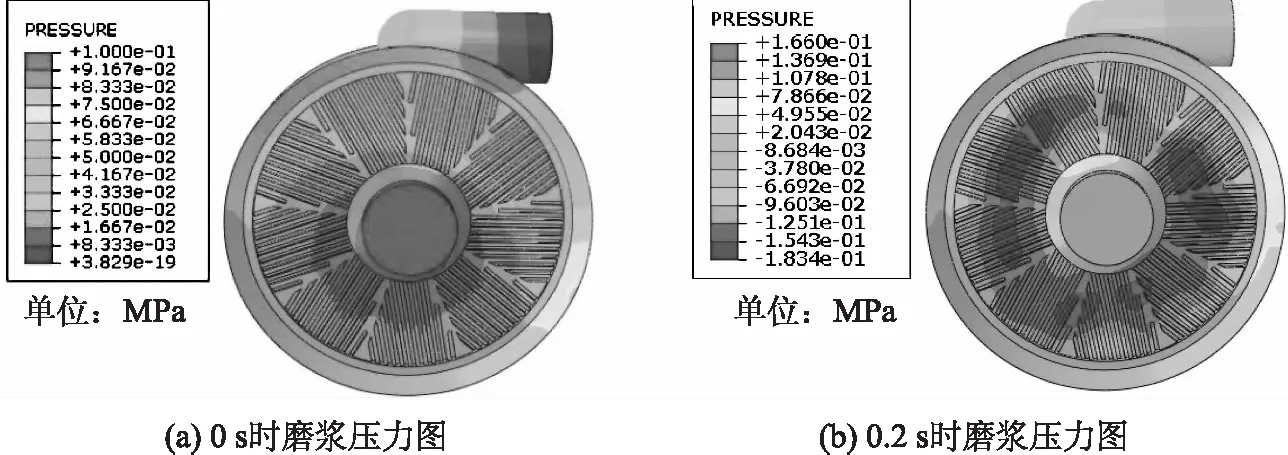
图3 磨浆过程压力图

2.2 磨浆过程速度分析

为了分析浆料在磨齿之间的流动情况，研究模拟了动磨盘和定磨盘速度矢量图。

图4为浆料在定磨盘内部流动图。从图4可以看出，在入口端到出口端的方向上，浆料主要沿着齿槽流动，且流动的速度较大。在入口端到背离出口端的方向上，在刚进入齿槽时，还沿着齿槽流动，但越径向向外，方向越发生变化，速度逐渐减小，且有不沿齿槽流动或横向流动的趋势。这主要是由于此处压力较大，浆料不容易流动，其中部分速度矢量甚至有反方向流动的趋势，可能引发反喷。

图4 浆料在定磨盘内部流动图

图5为浆料在动磨盘内部流动图。从图5可以看出，在入口端到出口端的方向上，浆料沿着齿槽流动，流动的速度较大且速度逐渐加大。在入口端到背离出口端的方向上，浆料大部分还沿着齿槽流动，流动的速度逐渐减小。动磨盘上的浆料总体随着齿槽流动，只有小部分在背离出口端附近出现了浆料速度小或者横流的现象，但没有出现定磨盘浆料不流动的情况，这是由于动磨盘在转动的情况下，离心力推动的作用。

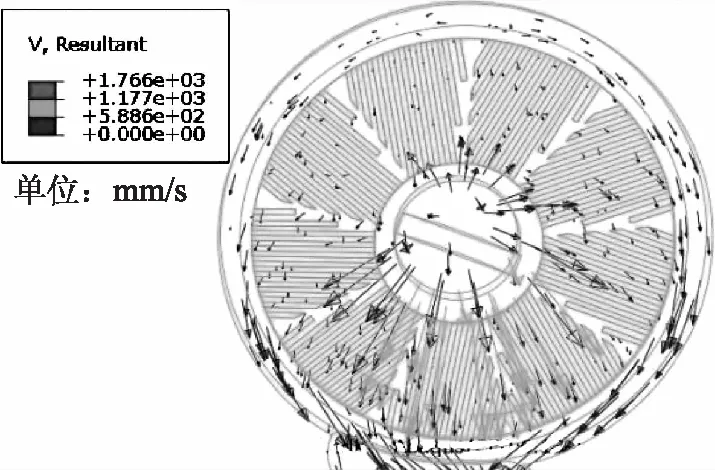
图5 浆料在动磨盘内部流动图

2.3 磨浆过程应力分析

图6为动磨盘磨片应力图。从图6可以看出，入口端压力最大，出口端压力最小。压力最大为3 MPa，主要分布在刚进入磨区的磨齿上(磨片的内孔端)。动磨盘中央压力也比较大，主要是浆料的进料口正对着动磨盘中央所导致的，且随着时间的推进压力逐渐扩大到磨齿上。

图6 动磨盘磨片应力图

图7为定磨盘磨片应力图。从图7可以看出，入口端压力最大，出口端压力最小。压力最大为0.5 MPa，主要分布在磨齿的入口处和齿面上。随着时间的推进，压力逐渐扩散到整个磨齿上，然而并不是所有的磨齿区域压力均相同，同时存在一小扇形区域的磨片压力比较小，并且这片区域靠近浆料出口端。

从定磨盘和动磨盘的应力分布图分析结果来看，动磨盘的压力比定盘的压力大。定磨盘有一片扇形区域压力比较小，而动磨盘在整个盘区压力大致相等。

2.4 不同磨片间隙下压力和速度分布情况

为了分析不同间隙下的平均压力，进出口速度分布情况，本课题分别建立了0.1、0.3、0.5、1.0、2.0 mm磨片间隙时的磨浆模型，来分析浆料流动状况。表2为磨盘变量随磨片间隙的变化。从表2可以看出，入口速度随磨片间隙的减小而减小，这是由于磨片间隙的减小导致磨浆室内部能容纳的浆料减小，浆料室内部的压力变大，阻碍浆料的进入，因此单位时间内进入磨浆室的浆料减少。

从表2可以看出，出口速度随着磨片间隙的减少而减小，这和浆料进入量的减少有关。由于浆料的进出质量相等，多少浆料进入就会有多少浆料出来，进入浆料的减少导致出口浆料的减少，实验表现为单位出口速度的减小。

从表2还可以看出，定盘压力随磨片间隙的减小而增加。由于磨片间隙的减小，磨浆的速度放缓，导致大量的浆料无法顺利的通过磨浆室，从而使磨浆室的压力增加，致使定磨盘的压力增加，实际运行中磨盘间隙的减少会加快磨盘的损耗。

从表2可以看出，动盘的情况基本和定盘相同。因为转子转动的作用使动磨盘的压力大于定磨盘的压力，符合实际生产中动磨盘磨损大于定磨盘的现象。

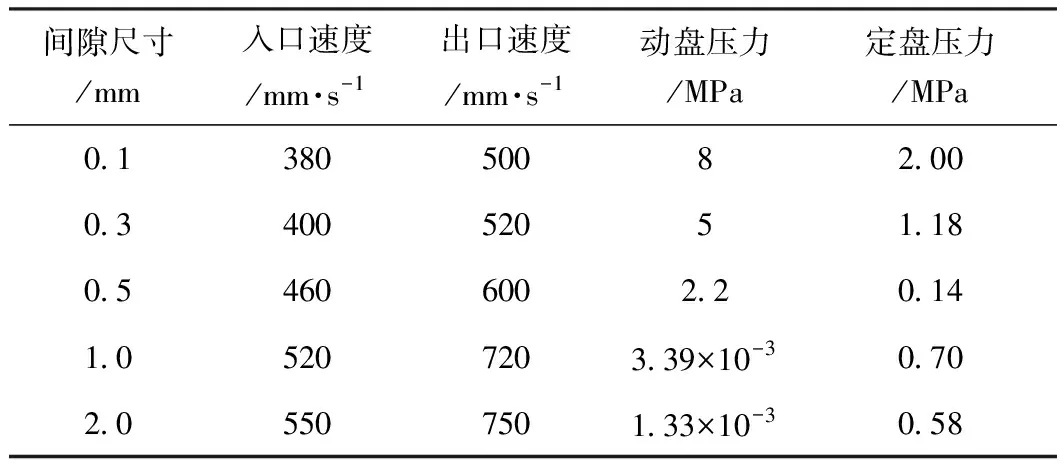
表2 磨盘变量随磨片间隙变化

3 结 论

本课题通过计算流体动力学(CFD)建立低浓盘磨机三维模型，分析了磨盘槽内纸浆流动和应力分布状况。

3.1 磨浆初期，磨浆区入口压力最大，出口压力最小，但经过一段时间后，在磨齿径向靠近入口1/3处磨浆压力达到最大。

3.2 在远离浆料出口的地方，定磨盘上的浆料速度较小，甚至有不流动的状况，而动磨盘由于离心力的作用，浆料均沿着齿槽流动。

3.3 动磨盘的压力要大于定磨盘的压力；同时随磨片间隙的减小，磨盘压力会增大，出、入口速度会减小。