基于距离优化的模糊综合评判法对自行火炮作战能力的评估

姚天乐，陶凤和，齐子元，张 俊

(1.陆军工程大学石家庄校区 火炮工程系, 河北 石家庄 050003；2.解放军第31700部队，辽宁 辽阳 111000)

武器系统作战能力评估问题被认为是军事能力量化研究的起点。在这方面，国内外相关领域已经有了一些研究先例，但复杂武器系统效能评估技术仍处于发展阶段。陈明等[1]提出了采用层次分析法与模糊综合评判相结合的方法对自行火炮作战效能进行综合分析；景耀杰等[2]建立了火炮装备效能静态综合模型；陈力、张建宇等[3-4]研究了自行火炮系统效能仿真动态评估方法和模型；陈士涛等[5]研究了维修保障系统效能的综合评估方法和技术；刘伟等[6]研究了战时装备维修保障效能评估方法及分项保障效能评估指标体系。但在面对武器系统的诸多指标以及复杂因素影响时，如何采取有效的方法更加精准的对武器系统作战效能或作战能力进行评估成为必须要解决的问题。自行火炮武器系统作战能力评估是一个经典的武器系统能力评估问题，如何精确地评估自行火炮的作战能力是领域内诸多学者不断探索的问题。

笔者提出基于距离优化的模糊综合评判法对自行火炮的作战能力进行评估。引入基于评估数据距离进行优化的专家系统，采用客观方法修正主观误差的方式，最大程度的利用专家集体的经验与智慧，使得评估结果更加精确合理。

1 自行火炮作战能力分析

自行火炮作战能力的主要指标包括：火力打击能力、机动能力、防御能力和指挥与控制能力。指标的具体内涵表述如下：

1)火力打击能力：包括武器和弹药。自行火炮的主要武器是大口径榴弹炮、机枪和烟雾榴弹发射器。弹药是指各武器的子弹，例如，榴弹等。

2)机动能力：包括一般运动能力和过障碍能力。前者描述了自行火炮的速度，行驶范围等。后者则是描述自行火炮能够穿越崎岖的地形以及垂直的障碍物的能力，如低墙、壕沟、涉水等。

3)防御能力：包括避免发现和被敌人击中的能力，对敌方影响的抵抗能力，以及在完成任务时保护乘员的能力。

4)通信与指挥能力：包括命令与控制、通信、导航以及监视和侦察。

综上所述，可以构建自行火炮作战能力评估指标体系，如图1所示。

评估的层次结构共分为3层，其中F表示层数，U表示指标代号。

2 基于距离优化的模糊综合评判方法

在模糊综合评判涉及专家的主观判断时，均引入专家优化模型，快速优化专家权重，实现评估过程的负反馈。

2.1 基于距离优化的专家权重确定

基于团体共识的距离优化方法基本描述为评估专家首先根据多个评估标准独立地对相同的评估问题做出自己的判断，即替代方案，然后将不同专家的这些判断合并成一个群体共识，以支持最终决定。此方法最早由Lean Yu 和Kin Keung Lai 提出[7]，主要用于支持非常规的多人应急决策问题。基于团体共识的距离优化方法所确定的评估标准的权重是基于数据本身确定的，可以极大地减少决策偏差，增加应急决策的客观性。因此，在自行火炮作战能力的评估过程中引入专家系统，并将本方法与模糊综合评判相结合，就可以更加有效地提高评估结果的可靠性。

2.1.1 基于距离的权重优化模型

通常，在指标体系庞大、复杂时，各个指标权重的确定运用主观方法可以充分利用专家们的集体智慧，评估出来的结果应该更为合理。但是，存在某些专家评估失误过大的情况，如果简单对专家们的评估结果进行合并，会使得评估结果不合理。为了形象描述，如图2所示，在某次具体评估过程中x轴与y轴分别表示评估边界，e*表示最佳评估结果，且e*是未知的。则更为合理的专家的评估结果应当聚集在e*附近，具有较大的相似性，即专家系统应当有评估共识。因此，应当利用这一特征来授予专家权重，使得评估结果与集体差异太大的专家拥有更小的权重，从而减小甚至剔除错误评估结果的影响。

利用评估结果分布这一特征，建立专家系统的优化模型如下。

假设有m个专家(Assessment Expert，AE)产生n个不同的决策结果(权重)，其中某个专家给出n个指标的决策结果为

Ek=(ek1,ek2,…,ekn)

(1)

为了聚合不同的评估结果，令E=H(E1,E2,…,Em)为m个专家的聚合结果，其中，H(·)为聚合函数。通常，取H(·)为线性函数对各评估结果进行聚合。则有

(2)

定义任意两名专家之间的决策结果Ek与Ej间距离的二次方为

(3)

式中：k，j分别表示第k和第j个专家，k= 1,2，…，m，j= 1,2，…，m；i表示专家的第i个评估结果，有i= 1,2，…，n。

通常，来自不同专家的评估结果在很大程度上是不完全一致的。为了使专家们的含权评估结果具有更大的相似性，专家们的评估结果应当相互作用。这是产生一个合理评估结果的基本原则。基于这一原则，采用基于距离的最小二乘聚合方法来合并由不同专家产生的评估结果，这种方法的基本思路是使得一个专家的评估结果到另一个专家的评估结果的平方距离的总和最小化，从而使它们达到最大的一致性。

利用上述的平方距离，可以构建优化模型来优化各个专家的权重，使得专家系统中所有专家的评估结果之间的平方距离之和最小化。优化模型构建如下：

(4)

2.1.2 优化模型的求解

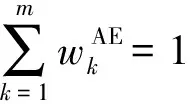
(5)

对wkAE进行微分运算，并简化合并各项可得

wjAE-λ=0

(6)

为了便于计算，将上述各式以矩阵的形式进行表示。令

(7)

可以得到:

(8)

此外，令

WAE=[w1AE,w2AE,…,wmAE]T

(9)

I=[1,1,…,1]T

(10)

则优化模型中目标函数和约束条件可分别表示为

S=(WAE)TBWAE

(11)

ITWAE=1

(12)

式(7)可以表示为

BWAE-λI=0

(13)

在式(11)中，由于S是一个距离的平方，应当大于0，因此矩阵B应该是正定且可逆的。联立式(12)、(13)可解得

(14)

由于B矩阵中的元素都是严格为正，因此B是一个非奇异的M矩阵[8]。由M矩阵的性质可知B-1是非负的，则方程式中的非负约束wkAE≥0成立，再次验证了上文所述。本方法使用了快速优化技术来整合不同的评估结果，使不同评估结果的聚合变得简单。

2.2 模糊综合评判

在进行模糊综合评判的过程中，需要进行因素评价以及权重集的建立，均涉及到专家的主观作用。因此，当评估专家产生作用时就引入专家系统，并根据评估结果进行优化过程，从而达到降低主观因素偏差的作用。

2.2.1 选取评估对象的因素集与评语集

2.2.1.1 建立能力指标体系因素集

对自行火炮能力进行模糊评判,需要确定能力评判因素,其总和即为评判因素的论域,记作

U={u1,u2,…,ui,…,un}

(15)

根据图1建立的评估框架，对自行火炮能力的模糊综合评判为三级模型,可建立自行火炮能力指标因素集。

2.2.1.2 建立能力优劣程度评价集

将所有的评价结果分成若干个等级，所有的等级构成的集合就是评语集。评语等级构成的评语等级论域一般记为

V={v1,v2,…,vm}

(16)

建立自行火炮作战能力优劣程度的评价集。将评价集划分为4个等级，并对各个等级加以量化为V={v1，v2，v3，v4}={优，良，中，差}={100，50，25，12}。指标集中所有的指标都会对应着评价集中的某个评价结果。

2.2.2 单因素评价

对于上述建立的评价集的各个等级均为模糊性能等级，而单因素的评价通常用打分的方法进行。对每个因素ui,打分确定该事物对评语性能等级vj(j=1,2,…,m)隶属程度rij,rij也就是表示ui具有评语rij的程度,它是从U到V的一个模糊映射,即

f∶U→F(V)

ui|→(ri1,ri2,…,rim)∈F(V),i=1,2,…,n

(17)

此时，打分须有专家系统的参与。由f可以导出一个模糊关系R，则由专家系统产生的R可以表示为R={R1,R2,…,Rn}。其中，Ri可表示为

(18)

2.2.3 建立指标权重集

由于各个因素的重要程度是不一样的，为了反映各因素的重要程度，对各个因素U赋予相应的权值wi。由各权重系数组成的集合称为因素的权重集W：

W=(w1,w2,…,wn)

(19)

权重集由几位专家采用AHP来确定，专家确定各个指标的权重后，进行优化过程来确定专家的权重，最后专家的权重与专家所给出的权重进行线性组合得出各个指标的最终权重。

2.2.4 进行模糊综合评判

从单因素评判矩阵R可以看出：R的第i行反映了第i个因素影响评判对象隶属于各个评语集的程度;R的第j列则反映了所有因素影响评判对象隶属于第j个评语集元素的程度。当权重集W与评判矩阵R已知，则可以进行模糊变换来进行综合评判如下：

(a1,a2,…,am)

(20)

式中：“∘”表示某种合成运算；A为模糊综合评判集；aj(j=1,2,…,m)为综合考虑所有因素的影响时，评判对象对评语集第j个元素的隶属度。

由于在自行火炮能力评估的过程中，所有的指标都会对最终的能力产生影响，因此合成运算“∘”取乘积求和性，即

(21)

2.2.5 确定能力优劣程度

对照评语集，给出各个等级所对应的分数，最后对自行火炮关于各个等级的隶属程度与各个等级的分数进行线性加权，则可以得到最终的自行火炮作战能力评分，即作为自行火炮最终的能力值。根据自行火炮的能力值可以判断自行火炮的能力优劣等级。

3 自行火炮作战能力评估

为了验证上述提出的方法，将对德国PZH2000、中国PLZ05和韩国K9 这3种型号自行火炮的作战能力进行评估作为数值示例，用于说明和验证方法的有效性。

3.1 计算指标权重

引入的专家系统由5位专家组成(AE1～AE5)，均采用AHP的方法评估上述指标在自行火炮的能力评估中的权重，最后利用距离优化的方法可求得各个指标的最终权重。各专家对各个指标评估出的权重及指标最终权重如表1所示。

表1 指标权重评估表

3.2 自行火炮作战能力评估

由5位专家根据简氏年刊中的数据分别对3个国家的自行火炮相关数据进行模糊综合评判。评判结束后，根据评判结果再次对专家系统进行优化处理，得到专家的新的最优权重。最后将专家权重与评判结果进行线性加权获得最终结果。

专家AE1～AE5对3个国家的自行火炮的指标评判隶属度向量进行评估计算。由于图1建立了较为完整的自行火炮能力评估框架，指标较多，全部在文中表示篇幅过大,因此，以表2所示的由专家AE1评估的由底层指标隶属度向量计算出的一级能力指标的隶属度向量为例。隶属度向量在表格中按照优、良、中、差的顺序排列。

表2 AE1对各自行火炮一级能力指标评估结果

WAE=(0.199 6,0.198 1,0.201 6,0.200 2,0.200 5)

将上述专家的评判结果与专家权重进行线性求和，可得到3个国家自行火炮的一级能力指标的隶属度向量，如表3所示。

表3 各自行火炮一级能力指标综合评估结果

由自行火炮的一级能力指标的隶属度向量与表1中的指标权重进行合成运算，将表中数据代入 可以得到自行火炮作战能力隶属度向量，如表4所示。

表4 各自行火炮作战能力评估结果

由表4可求得德国PZH2000的作战能力评分为：

UPZH=0.408 0×100+0.474 6×50+0.076 7×25+

0.040 7×12=66.935 9

中国PLZ05的作战能力评分为：

UPLZ=0.361 3×100+0.471 7×50+0.114 6×25+

0.052 3×12=63.207 6

韩国K9的作战能力评分为：

UK9=0.343 8×100+0.458 2×50+0.105 4×25+

0.092 6×12=61.036 2

3种型号自行火炮的作战能力排列为：

德国PZH2000 > 中国PLZ05 > 韩国K9。

由上述结果可知，基于距离优化的模糊综合评判法在评估过程中多次采用了优化模型，使得评估数据本身存在的偏差利用专家权重得到减小，进而又使得数据偏差减小，形成了负反馈，最终得出与普遍认识较为接近的结果，验证了方法的有效性。

4 结束语

武器系统能力评估问题是一个战略问题，对军事能力规划和发展具有重大影响。 笔者通过引入专家系统来改善模糊综合评判法，并基于数据自身的距离来优化各个专家的权重，使得主观经验得到了更好的发挥。同时，通过对3个国家自行火炮系统的作战能力进行评估，验证了本方法降低主观偏差的有效性，为武器系统评估提供了一种新思路。