基于拉格朗日插值的分数延时滤波器研究

黄 伟，周其超，陶存炳

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225101)

0 引 言

数字相控阵雷达空间分辨率高，抗干扰能力强，具有十分广阔的军事用途，相控阵天线通过控制信号在阵元内的传输时间实现信号延时，从而保证不同方向的信号同相叠加，获得预期的波束指向和方向增益[1]。传统的相控阵雷达利用模拟的方法产生信号波形，利用延迟线、移相器实现信号的延时移相。这种方法有诸多弊端，采用该体制的雷达系统体积大，使用和维护不便，信号产生不灵活，在数字域处理信号延时、移相，可以灵活地形成多样式雷达信号波形[2]。数字阵列雷达采用数字技术实现信号发射及接收，分数延时滤波器能够对信号作非整数倍的时间延时，在数字域利用分数延时滤波器可以实现信号精准延时，提高雷达波束指向精度[3]。

1 分数延时滤波器原理

分数延时滤波器能方便改变频率响应的特点，在语音音调同步合成、数字通信、时延估计、视频信号以及相控阵雷达信号处理等领域有着广泛的应用[4]。分数延时滤波器实现方法主要有窗函数法、拉格朗日插值法和基于多项式的分数延时滤波器设计方法。基于拉格朗日插值的分数延时算法易于实现，系数计算简单，少量的加法和乘法运算就能实现滤波器系数更新，在低频段具有良好的幅度和频率响应。

假设x(t)为连续时间信号，在满足奈奎斯特采样定理的条件下采样得到数字离散信号x[n]，通过理想数模转换器还原为连续信号，还原后的连续信号经延时处理后得到精准延时τ，最后送入模数转换器，以T为周期连续采样，得到离散数字信号y[n]，x[n]与y[n]的关系可以用如下的方式表示：

y[n]=x[n]*sinc(n-D)

(1)

可以发现，系统响应可以等效为离散的冲击响应，令：

hi[n]=sinc(n-D)

(2)

则有：

y[n]=x[n]*hi[n]

(3)

hi[n]可以视为无限长度的非因果滤波器[5]，下式为hi[n]在频域的表达式：

Hi(ejω)=e-jωD

(4)

式中：延时量D由两部分构成，整数部分Z和小数部分p，代入hi[n]频域表达式，则有：

Hi(ejω)=e-jωD=e-jω(Z+p)

(5)

由上述推导可以得到，理想分数倍延时滤波器的幅度特性以及频率特性为：

|Hi(ejω)|=1

(6)

arg{Hi(ejω)}=θi(ω)=-Dω=-(Z+p)ω

(7)

相位信息可以用群延时特性来表征，表达式如下：

(8)

同样，在一些情况下，相位信息也可以用相位延迟来表达：

(9)

设计分数延时滤波器，使其不断逼近理想分数延时滤波器相位延时滤波特性，求解滤波器系数，通过这样的方式设计分数延时滤波器，对信号进行分数延时滤波。

2 拉格朗日插值法设计的分数延时滤波器

在本文分数延时滤波器的设计过程中，选用有限冲激响应(FIR)数字滤波器来逼近理想分数延时滤波器，有限冲激响应数字滤波器的单位冲击响应的长度有限，可以在固定的系统条件下实现，实际设计的分数延时滤波器频率响应函数为H(ejω)，使其无限逼近于理想分数延时滤波器的频率响应函数Hi(ejω)，两者之间的误差函数可以表示为：

E(ejω)=Hi(ejω)-H(ejω)

(10)

对频域误差函数E(ejω)在某一频率点N阶求导使其导数为0，误差函数在该频点的频率逼近效果最佳，这样就可以保证在一定频率范围内保持最大平坦。对前述差函数在某一频点ω=ω0进行N阶求导，公式如下：

(11)

典型地，设ω0=0，在ω0=0处求N次导数，得到N+1组线性方程，以脉冲响应的形式表示如下：

(12)

表达为矩阵形式为：

Vh=v

(13)

其中：

(14)

(15)

通过给定1组数值，采用多项式插值的方法可以求解得到上式系数，上述求解过程相当于求解经典拉格朗日插值公式[6]，在z域分析，则有：

H(z)=z-D，D=0,1,…，N

(16)

对于固定的整数倍时延，误差逼近于零，求解得到的滤波器系数h(n)为：

(17)

3 分数延时滤波器仿真分析

针对基于Lagrange插值法设计的分数延时滤波器进行了3组仿真，延时参数设为0～0.5采样周期，间隔0.1采样周期，滤波器阶数设为7阶、15阶和19阶，截止频率设为0.7π。

从图1～图3可以看出，基于Lagrange插值法设计的分数延时滤波器在低频具有平滑的幅度响应和相位延迟，但是在滤波器阶数较低时，幅度响应和相位延迟不能满足截止频率为0.7π的要求，当滤波器阶数达到15阶，相位响应和幅度响应有明显改善，特别是频率高于0.4π的部分。随着滤波器阶数的增加，滤波器性能持续提高。

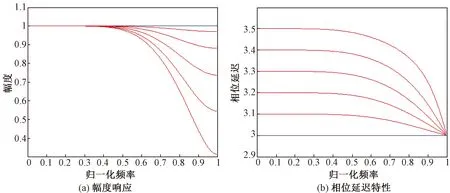
图1 Lagrange插值法7阶分数延时滤波器幅度响应和相位延迟特性

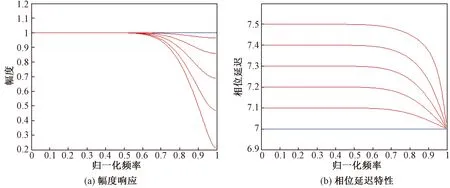
图2 Lagrange插值法15阶分数延时滤波器幅度响应和相位延迟特性

图3 Lagrange插值法19阶分数延时滤波器幅度响应和相位延迟特性

为了分析基于拉格朗日插值法设计的分数延时滤波器延时效果，本文进行了如下仿真对比，采样频率设计为8倍信号频率，分数延时滤波器阶数为15阶。分别对2列正弦信号进行采样，其中一列信号在采样前相对于另一列信号有0.5倍采样间隔延时，采样得到的离散信号经分数延时滤波器延时处理后对比2列信号之间的时间间隔。这样设计的目的是为了更直观地观测延时效果。

图4和图5分别为分数延时前后2列信号的对比图，不难看出，经过分数延时滤波器延时处理之后，2列信号几乎重合，说明分数延时滤波器精准地校正了2列信号之间的延时误差。

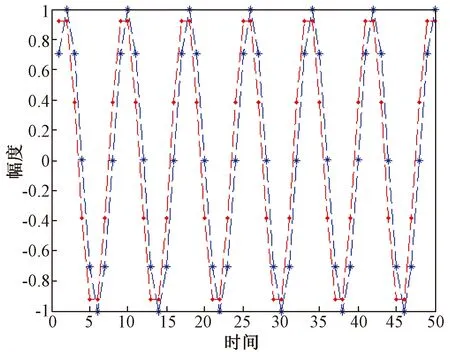
图4 分数延时滤波之前2列信号对比图

图5 分数延时滤波之后2列信号对比图

4 结束语

分数延时滤波器采用不断逼近理想滤波器相位延时滤波特性的方法，求解滤波器系数。基于拉格朗日插值法的分数延时滤波器设计过程中，对频域误差函数N阶求导，使其为0，以此得到滤波器系数。本文在分析分数延时滤波器的基本实现原理的基础上，仿真分析了基于拉格朗日插值法设计的分数延时滤波器的相频和幅频特性，结果表明滤波器在低频具有非常好的幅度响应和相位延迟响应，并且随着滤波器阶数的增加，滤波器性能持续改善。最后应用滤波器对离散信号进行延时处理，处理后的信号得到了精准的分数倍延时，验证了基于拉格朗日插值法设计的分数延时滤波器延时滤波的有效性和可行性。