一种改进的PMSM滑模变结构位置辨识策略研究

张海刚，胡添添，王步来，万 衡，徐 兵，张东民

(上海应用技术大学，上海201418)

0 引言

永磁同步电机(以下简称PMSM)因其具有结构简单、高功率密度和高效节能等优点，被广泛应用于工业生产及日常生活中，特别在新能源汽车领域更是占据了主导地位。

PMSM矢量控制系统中需要精确的转子位置信息，在传统方法中，转子位置信息来源于机械传感器，而在一些场合中无法使用机械传感器。故各国学者普遍开始研究无速度传感器，各种无速度算法亦被应用于实际控制中［1－4］。

PMSM控制是一种典型的非线性系统，为进一步加快PMSM调速系统的响应速度，提高系统稳定性和鲁棒性，模糊控制方法在电机控制领域得到了越来越多的关注，成为目前的一个研究热点［5－6］。模糊控制实际上是一种非线性控制，与常规PI控制器不同，模糊控制对控制对象的参数变化或非线性具有较好的适应能力。但是在电机控制系统速度突变或外加负载扰动的情况下，模糊控制难以有效消除静态误差，降低控制系统快速性，使得控制系统引起较大的超调，甚至引起系统较大的振动，系统性能下降［7］。这主要是由于在系统偏差较大时，模糊PI控制器中积分环节的积累使得控制量超过执行机构可能允许的最大动作范围的极限控制量，难以达到理想的控制精度。

为解决上述问题，本文在位置辨识环节设计了改进的滑模观测器，并在速度环上设计了一种积分分离型模糊PI控制器。即在传统滑模观测器基础上构造一种双曲正切函数替代开关函数，在模糊PI控制器上引入一个积分分离环节，从而加快系统响应速度，减小系统静态误差和削弱控制系统的抖振，最后搭建仿真和实验平台，验证了该改进的控制方法的速度响应快、超调小、鲁棒性强、抗干扰能力好等优点。

1 PMSM数学模型

由电机理论可得隐极式PMSM在α－β坐标系下的电压方程:

式中:

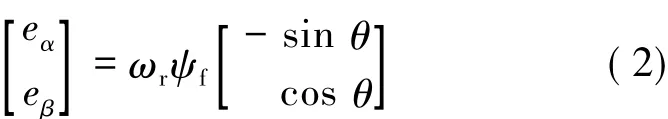
由此可推出PMSM在α－β坐标系下的电流模型:

式中:uα，uβ以及 iα，iβ分别为定子电压和定子电流在α，β轴上的分量;Rs，L分别为定子电阻以及定子电感;eα，eβ分别为反电动势在 α，β轴上的分量;θ为转子角位置;p是微分算子。

2 滑模观测器的改进与优化

2．1 滑模观测器的设计

从式(2)可知，反电动势中包含了PMSM的转速及转子位置信息，因此，只要测得电机的反电动势，就可以通过数学计算得到电机的转子信息。根据滑模变结构控制理论定义切换面如下:

在滑模变结构控制中，一般运用如下切换控制函数:

式中:k表示滑模增益，k值的选取要保证系统的稳定性，如何选取k值将在下节具体阐述。切换函数定义如下:

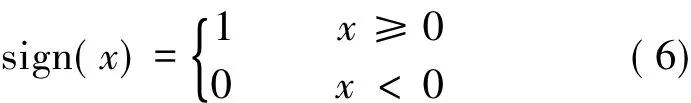
从式(3)～式(6)可得构造的观测器方程:

将式(7)与式(3)相减，即可得到电流误差估计方程:

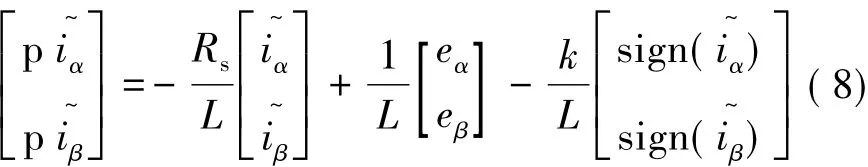
2．2 滑模观测器的优化

由于采用的是开关函数，传统的滑模变结构控制存在抖振过大的问题，为解决此问题，本文采用双正切函数替代开关函数。

定义双正切函数如下:

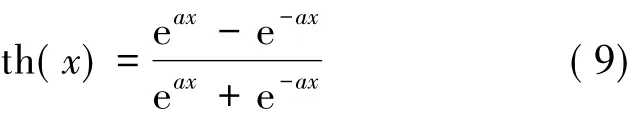
则反电动势方程:

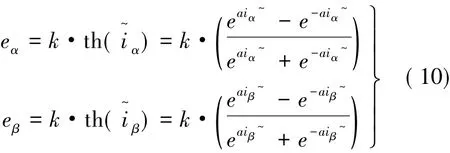
与传统的开关函数相比较，双正切型函数可以利用常数a来调整斜率，使得双正切函数在－1～1之间连续变化。这样便可以通过调整斜率来改善观测器的性能。

如图1所示，当a值越小，函数的斜率越小，控制效果就越平滑;当a=10时，双曲正切函数的斜率接近开关函数。

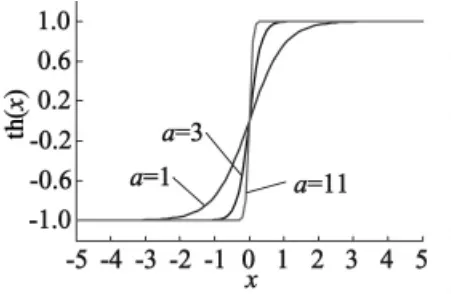
图1 不同a值下的双曲正切函数

3 模糊PI控制器的改进与优化

3．1 模糊PI控制器的设计

模糊控制是一种基于规则的控制，它直接采用语言控制规则，推理和决策过程与人类行为相似。在系统设计中不需要建立被控对象的精确数学模型，使得控制器的设计更为简单，应用更为方便。

模糊控制的基本框图如图2所示。

图2 模糊控制框图

模糊控制算法的核心为模糊控制器，控制规律由计算机的程序实现，系统将微机采样得到的被控量采样值与系统给定值相减得到的误差作为模糊控制器的一个输入量，后将误差信号进行量化，经过模糊推理最后得到模糊控制量，电机控制系统的模糊PI控制器一般采用速度误差即速度误差导数作为控制器的输入量，模糊PI控制器的系统框图如图3所示。

图3 模糊PI控制系统框图

由图3可知，模糊PI控制器为二维模糊控制器，其中偏差e是给定值n*与反馈值n的偏差值，即e=n*－n。将偏差e和偏差e的变化率作为控制器的输入，控制器输出u经过PI运算后构成模糊PI控制器，控制的输出为q轴电流

3．2 模糊PI控制器的优化

在电机控制系统中，模糊PI控制性能相比较常规PI控制有明显的提高．但当速度突变或系统外加负载扰动时，模糊控制难以有效消除静态误差，降低控制系统快速性，使得控制系统性能下降，由此本文提出一种积分分离型模糊PI控制器。即在模糊PI基础上引入一个积分分离环节，由于积分环节既能消除静态误差，亦降低了系统的响应速度，所以当被控量与设定值偏差较大时，取消积分环节;当被控量接近给定值时，引入积分控制，以便消除静态误差，提高控制精度。新型模糊PI的控制系统框图如4所示。

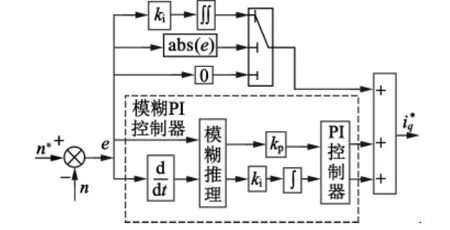
图4 积分分离型模糊PI控制器系统框图

由图4可知，速度偏差e是速度给定值n*与滑模观测器估算的反馈值n的差值，即e=n*－n。偏差e和偏差e的变化率作为模糊推理输入，同时在模糊PI基础上引入一个比例环节，偏差e和偏差e的变化率经模糊推理输出的参数作为PI控制器的输入，然后与加入的积分分离一起构成新型模糊PI控制器，控制的输出为q轴电流。

通过MATLAB中模糊工具箱，对模糊控制器进行设计，其中图5为系统输入偏差e以及偏差变化率隶属函数。其模糊推理规则如表1所示。

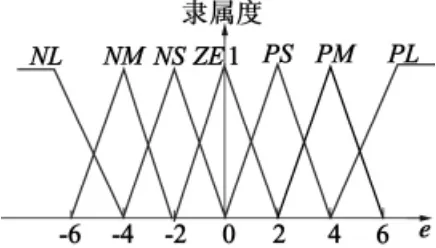
图5 系统输入偏差e以及de/dt的隶属函数

表1 模糊控制规则表

4 系统仿真与分析

4．1 PMSM的矢量控制系统

在Simulink下搭建PMSM矢量控制仿真模型，如图6所示。

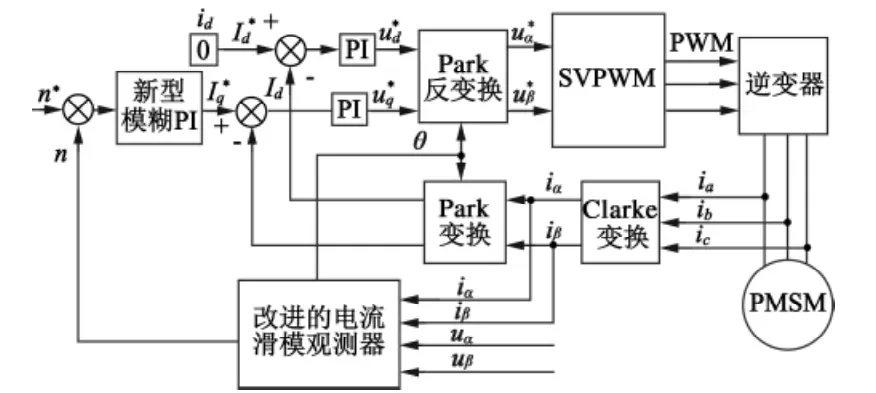
图6 PMSM矢量控制总体框图

在矢量控制中，本文研究了两种改进策略，一是在观测器部分采用一种改进的滑模观测器，即在观测器中用双曲正切函数代替开关函数;二是在控制策略方面对模糊PI控制的改进，即在模糊PI控制策略的基础上再引入一个积分分离环节。

4．2 仿真实验分析

基于MATLAB/Simulink仿真平台搭建了PMSM无传感器矢量控制仿真模型，电机参数如表2所示。

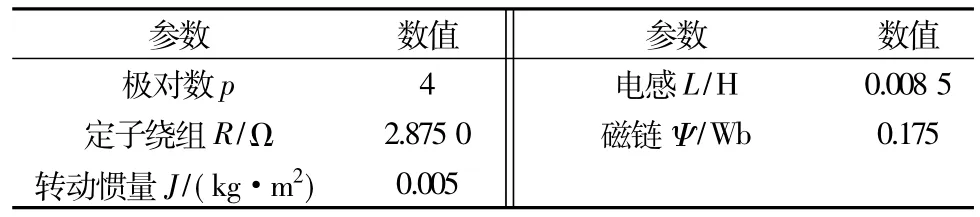
表2 电机参数

下面，通过负载突变的对比实验来说明改进策略的先进性。

4．2．1 负载转矩突变分析

在PMSM稳态运行条件下，在0．1s给电机施加8 N·m的负载，图7、图8分别为常规模糊PI控制系统与积分分离型模糊PI控制系统的仿真波形。

通过图7与图8对比分析可知，在转矩突变情况下，常规模糊PI控制系统在0．104 s时稳定，即过渡时间约为0．004 s;估计转速大概稳定在485～495 r/min之间，在有负载情况下，电机转速有所下降;转速误差在－4～6 r/min之间;α轴和β轴电流误差在±0．04 A之间。

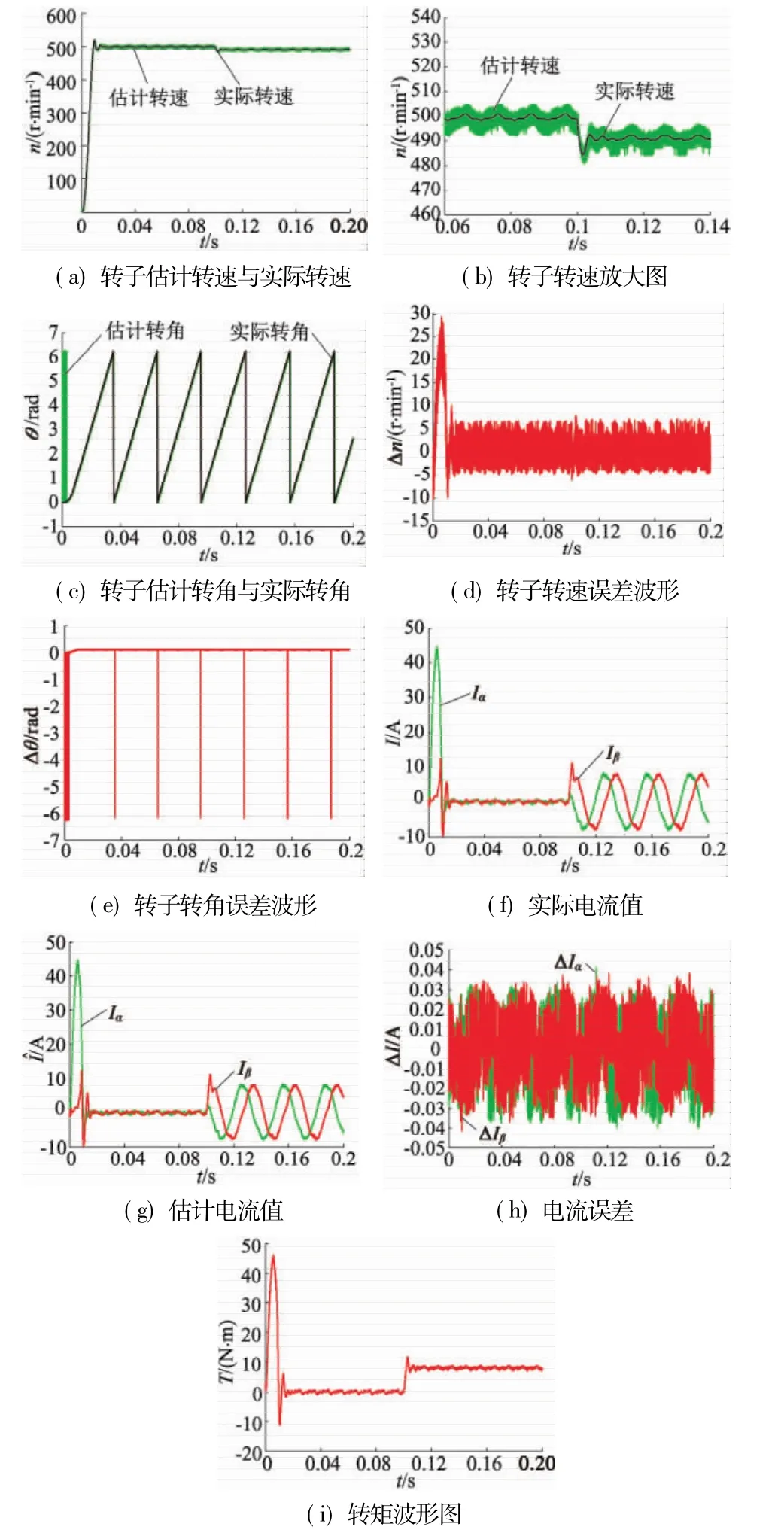
图7 转矩突变时常规PI控制器仿真波形

积分分离型模糊PI控制系统在0．106 s时稳定，即过渡时间约为0．006 s;转速估计值大致稳定在490～496 r/min之间;转速误差在0～5 r/min之间;α轴和β轴电流误差在±0．03 A之间。两图的转矩波形都较理想，但积分分离型PI控制系统的电流波形更平滑，与常规模糊PI控制策略相比，在突加负载情况下，积分分离型模糊PI控制策略的机械特性更硬、响应速度更快、稳定性能更高。

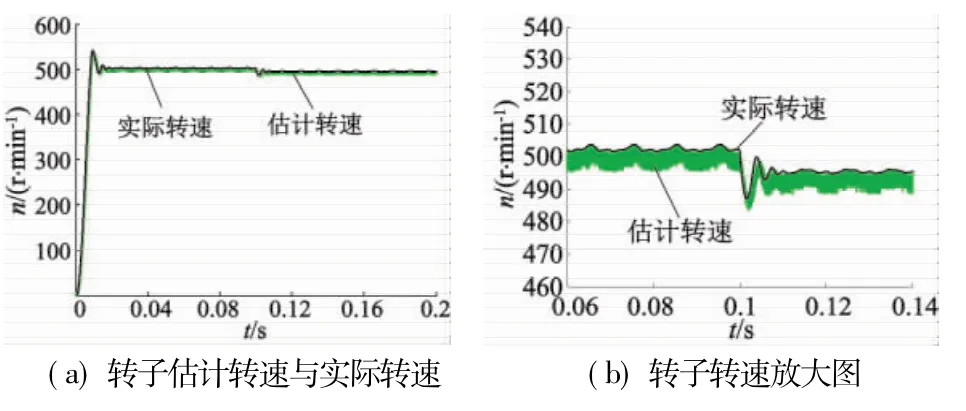
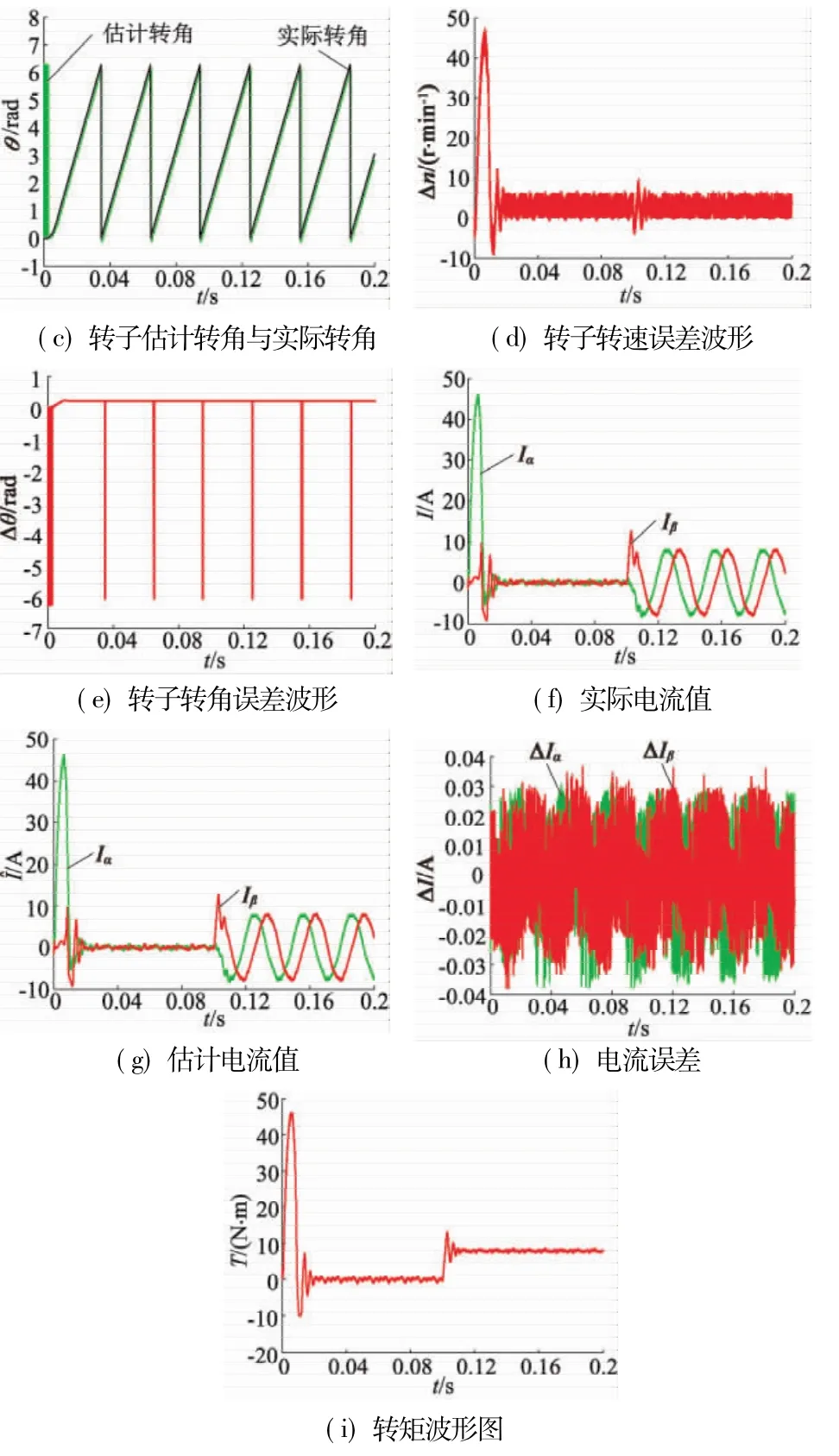
图8 转矩突变时新型PI控制器仿真波形

5 硬件实验分析

为更好地说明改进的PI控制器的优越性，本文基于TI公司的控制器搭建了实验平台，包括TMS320F2812控制芯片以及高压驱动板构成，图9为整个硬件实验平台的实物图。

图9 硬件实验平台

本实验使用的PMSM额定功率大小为1．1kW，同步转速1500 r/min，电机额定电压380 V。下面以上述硬件平台为基础条件，通过示波器测量电机在500 r/min下的定子电流波形。

图10是优化和改进后的定子电流波形图，经过优化和改进后的定子电流波形毛刺较小，波形更接近于正弦波。实验波形验证了本文的设计方案是合理的，实验结果也比较理想。

图10 积分分离型PI控制系统定子侧电流

6 结 语

本文在PMSM矢量控制系统的基础上，提出两组改进策略，一是在位置辨识环节设计改进的滑模观测器;二是在速度环上设计了一种积分分离型模糊PI控制器。仿真与实验证明，经过优化后，电机控制系统的响应速度以及跟踪效果都得到了提升，特别在负载情况下，电机在减小转速误差方面效果更加显著。