压缩感知图像的块子带自适应稀疏表示规则化重构

熊承义，龚忠毅，高志荣，张梦杰

(1中南民族大学 电子信息工程学院 智能无线通信湖北省重点实验室， 武汉 430074；2中南民族大学 计算机科学学院， 武汉 430074)

近年来，压缩感知(CS)理论[1-3]作为一种新的信号采样理论受到了国内外学者广泛的关注，其在信息论、图像处理、无线通信等领域具有广泛的应用前景[4-6].不同于香农采样理论，CS理论指出，如果信号x∈RN在某个变换域Φ能被稀疏表示，则通过少量的随机观测值y∈RN可准确重构原始信号x.换言之，虽然在M=N时,应由观测值y重构原始信号x是一个病态的欠定问题，无法确定唯一解，但是在信号满足稀疏性且观测矩阵满足有限等距原则[2](RIP)时，由降维观测值y可高概率地准确重构原始信号x.压缩感知信号重构的数学模型可表示为：

(1)

其中：Φ为稀疏变换矩阵；H为测量矩阵；‖·‖p表示取p范数.

对于自然图像，如果直接对整幅图像进行压缩感知观测，由于其观测矩阵的维度会很大，因此带来对观测矩阵的存储规模太大以及计算复杂.为了有效降低重构算法的复杂度，Gan在文献[7]中提出了基于图像分块的压缩感知(BCS)，有效减小了观测矩阵的维度和重构的计算复杂度.基于BCS的压缩感知图像重构模型的数学表示为：

(2)

其中xi表示图像中第i个图像块.

BCS算法先将原始图像x分成很多个彼此不重叠的小块图像，再对每一个小块图像进行独立观测，观测矩阵的维度不再随着原图像x维度的增加而增加，降低了对观测矩阵存储代价及计算复杂度.然而，块独立的分块压缩感知重构通常会出现较严重的方块效应.针对该问题，文献[8]通过采用具有平滑作用的维纳滤波，提出了基于分块采样与平滑Landweber投影的压缩感知重构方法.通过采用迭代的变换域滤波处理，实现了在图像即使采用较小分块压缩感知时也能得到较好重构效果.

为了更好提升信号压缩感知重构的准确性，得到更高质量的重构信号，探求更好的采样信号，稀疏表示是其中关键；而对于图像信号的压缩感知重构，如何充分利用图像信号具有的局部相似和非局部相似，更好地提升对图像的稀疏表示能力，进一步有效提升图像重构质量，是近年该研究领域的重要方向，比如基于全变差(TV)的方法[9]、基于多假设(MH)的方法[10]、基于非局部相似(NLS)的方法[11,12]等.然而，以往方法大多简单地直接利用图像信号经过某种变换后的稀疏性来约束重构，导致图像中存在的微小而重要的细节信息丢失.即尽管在一般情形下，较小的稀疏表示系数比起大的稀疏表示系数的损失对于图像质量的影响更小，但如果图像信号中存在重要而非显著目标，保留该目标在图像稀疏变换域对应的较小系数对于保留相应细节信息十分重要.

自然图像信号一般具有非平稳的特性，图像中的不同图像块会表现不同的分布特性.实际上，具有非平稳特性的自然图像信号在变换到稀疏域时，不同图像块的变换域系数也呈现服从不同分布模型[13]的先验.基于以上考虑，本文提出了一种基于分块图像子带自适应稀疏表示规则化的压缩感知图像重构方法.具体来说，首先利用非局部相似块组估计每个分块图像变换域各子带系数的均值和标准差，再将图像块各子带系数进行去均值并关于标准差归一化，最后将去均值归一化处理的子带系数的li范数表示用于规则化压缩感知重构.

1 块子带自适应稀疏表示规则化的压缩感知重构

自然图像信号一般具有非平稳的特性，不同图像块的变换域各子带系数通常服从不同的统计分布特性.为更好保留非显著而重要目标的纹理细节信息，区别对待不同图像子块的小的变换系数十分必要，故提出利用图像分块的稀疏系数进行自适应去均值归一化后规则化压缩感知重构的思想.具体重构模型如下：

(3)

其中：xk=R(x)为提取的第k图像块；R(·)为图像块提取算子；Φk是利用主成分分析(PCA)学习的自适应字典[13]；μk和σk分别是第k图像块变换域子带的均值和标准差，其值通过对提取xk的一组非局部相似块组的变换域系数进行统计估计.

式(3)的求解采用分裂布雷格曼迭代(SBI)算法[14]实现.通过引入辅助变量u等价表示x，则式(3)改写为：

(4)

利用SBI算法求解，(4)式可分解为如下两个子问题：

(5a)

(5b)

其中：t表示迭代次数；μ为规则化参数；b为SBI迭代过程中的迭代参数，在每次迭代中进行更新，具体为：

b(t+1)=b(t)-(u(t+1)-x(t+1)).

(5c)

1.1 u子问题求解

对于u子问题，实质是求解一个二次函数最小问题，其解可通过求函数的导数为零得到，即：

u=(HTH+μI)-1(HTy+μx(t)+μb(t)),

(6)

其中I为单位矩阵.为避免计算中的矩阵求逆运算，降低计算的复杂度，式(6)的计算可采用梯度下降法迭代式(7)实现：

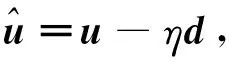
(7)

式中d是式(6)的梯度，η是梯度下降步长.因此，式(7)也可进一步重写为：

(8)

式(8)中的HTH和HTy只需要计算一次，因此极大降低了计算复杂度.

1.2 x子问题

在求解x子问题时，u已经由上一步计算得到.为了简化表示，令r=u-b，则式(5b)等价于：

(9)

利用大数定理可证明：

(10)

其中c1为常数.于是，若令αk=Φkxk,βk=Φkrk，则有：

(11)

于是，式(9)等价于：

(12)

其中c=μ·c1，式(12)可利用软阈值收缩法实现如下：

sgn(βk-μk),

(13)

在系数进行软阈值处理后，恢复的图像块可进一步由式(14)通过求逆变换得到：

(14)

最后，根据恢复得到的所有图像块xk，将它们放回图像的原始位置，然后通过求加权平均，还原整幅图像x，即：

(15)

其中：RT(·)为R(·)的转置算子；B×B为分块图像xk的维数.

2 实验结果与分析

为验证本文算法的有效性，利用压缩感知中常用的测试图像(Vessel, Leaves, Lena, Boats和Cameraman，除Vessel大小为256×256外，其余4幅图像的大小为96×96)进行实验.为降低计算复杂度，本文方法也采用了基于分块的压缩感知框架，分块大小为×.与当前主流的同类压缩感知重构算法进行了对比，包括全变差(TV)算法[9]、多假设(MH)算法[10]、协同稀疏表示(RCoS)算法[11]、组稀疏表示(GSR)算法[12].实验平台为Matlab2008b，硬件条件为Intel双核处理器、频率为3.40 GHz、内存为4.00 Gb，操作系统为Windows 7(64 bit).每个算法包含大量参数设置与自适应调整过程，在测试过程中所使用的算法参数均为原作者在相应论文中给出的最佳参数设置.

在实验中采用峰值信噪比(PSNR)和主观视觉效果来评价算法的重构性能.PSNR越高，重构效果越好.本文算法(PBASR)的参数设置如下：规则化参数λ=0.09，μ=0.0025；非局部相似组中块的大小为6×6，组中相似块数目为60，搜索相似块的窗口大小为20×20；由于梯度下降步长η设置不当会导致收敛过慢或不收敛的现象，因此η的大小通常与梯度有关，具体设置方法与GSR算法相同.

实验中设定采样率分别为0.1，0.2，0.3，不同采样率下各种算法的PSNR性能比较结果如表1所示.由表1可见：PBASR算法对所有测试图像均能得到更好的重构效果.在不同采样率下，本文算法在5幅不同的测试图像的平均PSNR相比TV算法、MH算法、RCoS算法、GSR算法分别提高3.56，3.73，1.80，0.69 dB，其中基于图像相似块组稀疏性的RCoS算法和GSR算法重构效果最好.

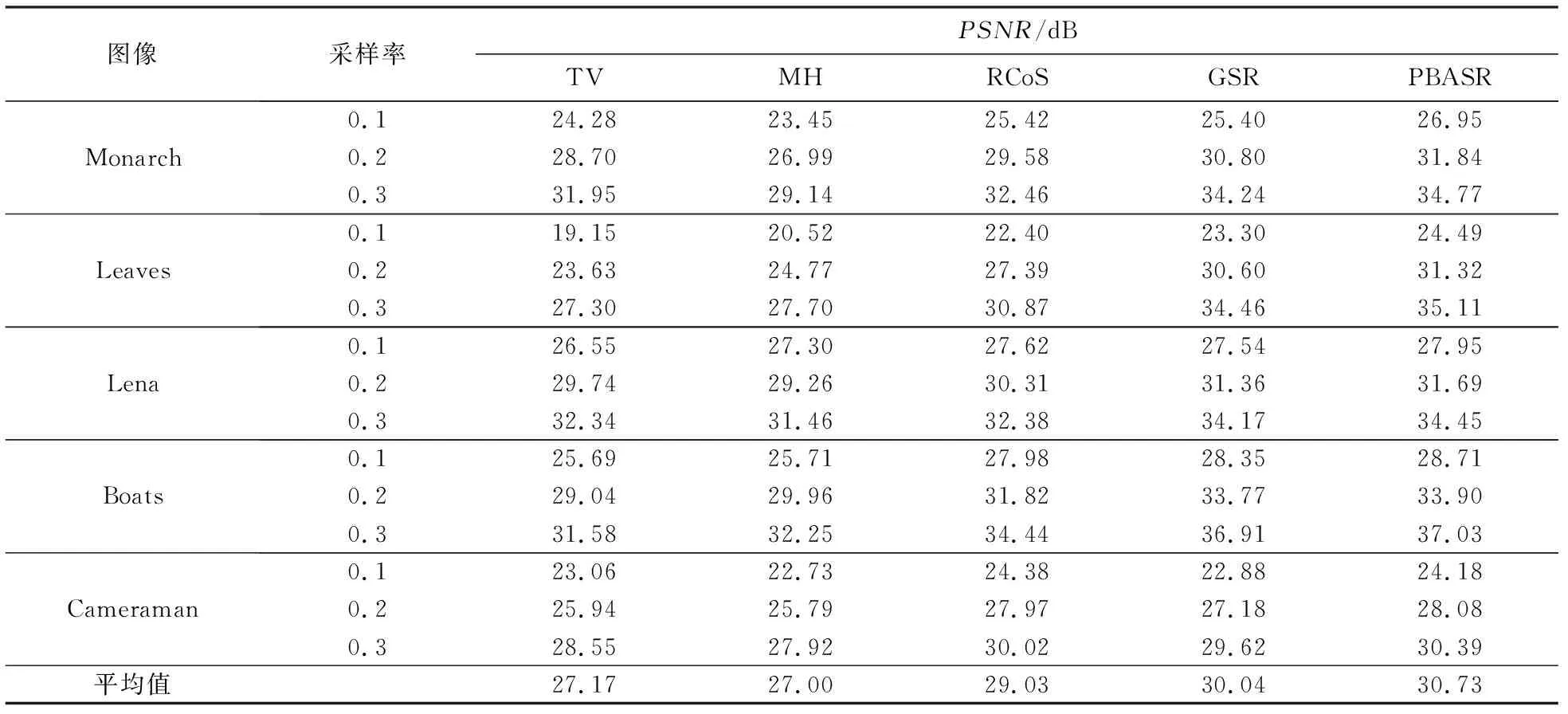
表1 不同采样率下几种重构算法PSNR性能比较Tab.1 PSNR performance comparison of several reconstruction algorithms under different sampling rates

为比较各种重构算法的主观视觉质量，给出了在采样率为0.1时不同算法的重构图像，结果见图1和图2.

图1 测试图像Monarch在0.1采样率下不同算法的重构图像Fig.1 Reconstructed image of Monarch with different algorithms at 0.1 sampling rate

由图中可见，本文算法对图像纹理细节具有更好的重构效果.由于TV算法仅利用图像平滑性先验知识，重构图像过于平滑，低采样率下，有明显的油画效果.利用相似块组稀疏表示先验的压缩感知重构算法重构效果较好，RCoS算法和GSR算法是其中的典型代表，GSR算法在同类算法中性能表现最好.比较结果可见：本文方法通过对图像块的变换域系数进行归一化处理后，稀疏表示规则化重构，保留了图像弱小高频纹理细节信息，明显改善了重构图像视觉质量.

3 结语

由于自然图像信号一般具有非平稳的特性，不同图像块的不同子带的统计分布特性具有较大差异，因此直接利用整幅图像统一分布模型下的稀疏表示约束CS重构，图像中的微小而重要的细节信息容易丢失，重构质量难以令人满意.本文利用分块图像的变换域系数在归一化后具有较好一致性统计分布特性的先验，提出了基于自适应块归一化稀疏表示的CS图像重构方法.基于图像块的自适应去均值归一化更加合理地表达了稀疏系数的重要性，在图像恢复中更好地保留了图像弱小目标及图像边缘和纹理细节信息，获得了更好的图像重构效果.

图2 测试图像Cameraman在0.1采样率的重构图像Fig.2 Reconstructed image of Cameraman with different algorithms at 0.1 sampling rate