混合到达模式下市郊列车开行方案优化研究

杜 鹏，杨雍彬

(北京交通大学a.交通运输学院；b.城市交通复杂系统理论与技术教育部重点实验室，北京100044)

0 引 言

市郊铁路连接都市圈核心区与外围城镇组团，具有快速、大运量的优势，非常适合长距离通勤出行.以东京都市圈市郊铁路为代表的采用多种停站模式并公布时刻表的列车开行方式，在满足多种出行需求的基础上重点照顾了通勤出行，具有较高的运输效率，也有力地支撑了东京都市圈的运作.由于种种原因，目前市郊铁路在我国轨道交通系统中的定位较为模糊，一些市郊铁路线路按照地铁方式建设并投入运营.既造成了建设成本的浪费，也没有发挥市郊铁路的长距离通勤优势[1].在这种情况下，以列车开行方案为切入点，分析市郊铁路乘客候车行为和乘车选择，进而提出包括停站模式和开行频率在内的市郊列车开行方案优化方法，从而为市郊铁路运营组织和定位提供有益的借鉴，就成为当前一个具有较强实际意义的研究问题.

市郊运输服务一般被认为属于公共交通的范畴.对于采用间隔式而不是车次式的公交服务(例如城市中心区的地铁)来说，通常认为当发车间隔较小时，乘客的到达规律服从均匀分布，乘客的平均候车时间等于发车间隔的1/2.但是学者们也发现，这些假设与实际情况并不完全吻合，尤其是当发车间隔较大时.O’Flaherty[2]，Seddon[3]早期发现公交乘客候车时间与发车间隔是近似的线性关系而非0.5倍；Luethi[4]明确提出乘客到站是均匀到达和非均匀到达双重行为的混合分布，并使用均匀—Johnson SB分布描述；随着车站AFC数据的采用，Zhao[5]统计伦敦铁路网进出站数据，发现在发车间隔介于7～30 min时，乘客到站分为两种类型：接近时刻表到站和随机到站并候车的乘客，且随机到站乘客的比例随发车间隔而变化；Jesper[6]分析丹麦哥本哈根地区地铁、市郊铁路和区域铁路的近200万条AFC数据，提出乘客到站概率符合与发车间隔相关的均匀-β分布，并将符合条件的发车间隔扩大至2～60 min，对比验证其具有较高的精确度.考虑到市郊铁路发车频率往往低于地铁，因此在提供时刻表的前提下，乘客到达规律不能沿用地铁所采用的均匀分布；同时，时刻表的采用也为开行多种停站方案的列车、减少乘客出行时间提供了便利.在列车停站优化问题上，国内外学者[7-9]依据车站等级和不同等级列车开行比例，提出了基于高铁车站服务频率的停站优化方法.其对开行成本的分析可以为市郊铁路提供参考，但市郊客流的特点显然有别于高铁.

本文采用市郊铁路开行多种停站列车并公布时刻表的运营模式，引入具有较高拟合度的均匀-β混合分布描述乘客在不同列车服务频率时的候车行为及乘车选择，刻画乘客到达规律.建立多停站模式下关联于服务频率的Qij乘客动态候车成本，定义市郊列车广义开行成本构成，建模并求解最优开行方案.

1 市郊乘客的到达模式分析

1.1 乘客混合候车行为

根据Jesper[6]混合候车理论，对于发车间隔在2～60 min且公布时刻表的公共交通，固定候车周期h(发车间隔，min)内乘客在不同时刻到站的概率密度函数R(r)是均匀函数与β函数的复合函数，如式(1)所示.市郊铁路发车频率低于地铁且停站多样，采用非固定席位、公交化运营时为保证较高的客运服务水平，需提供列车时刻表.此时混合候车理论适用于市郊乘客.

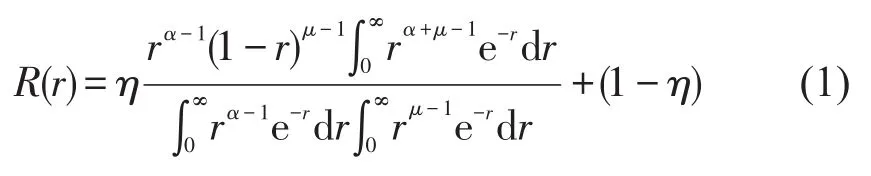
式中：r∈[0 , 1]，表示候车时间占候车周期h的比例(候车时间比)；α，μ和η是与服务频率相关的β分布统计参数.

参考并补充Jesper[6]统计结果对R(r)积分，得到客流Qij的平均候车时间如表1所示.

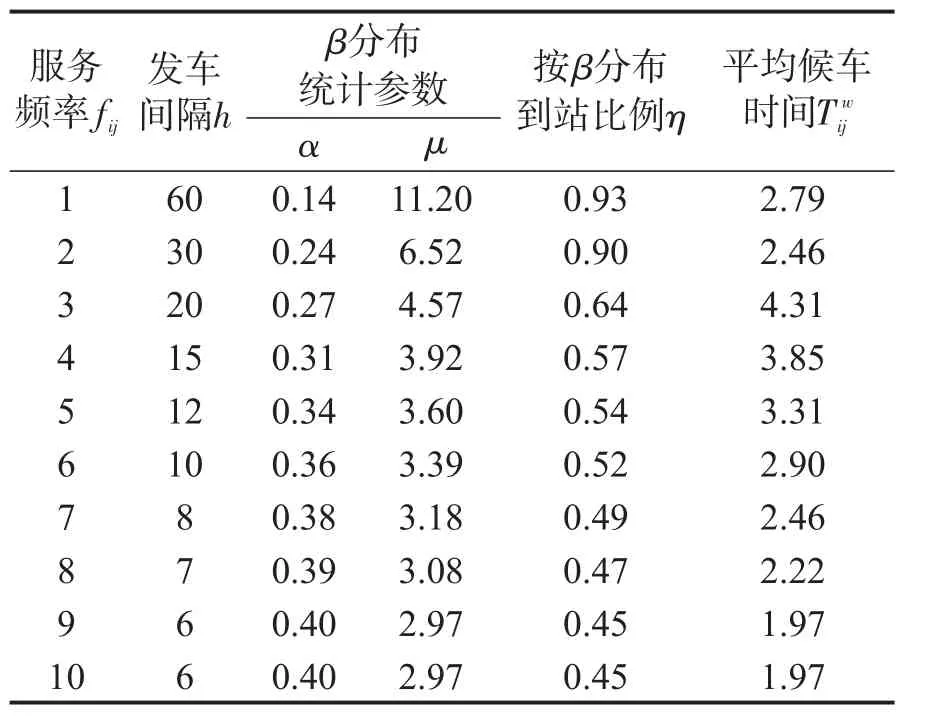
表1 不同服务频率下混合候车分布参数值Table 1 Distribution parameters of mixed waiting modes at different service frequencies

1.2 乘客乘车选择

传统铁路考虑不同等级列车阻抗，并通过票额策略引导和分配客流，使全程上座率最大；城轨系统则考虑线路成网条件下，通勤客流出行阻抗最低时的路径分布概率[10].市郊铁路区别于两者，既存在不同停站等级列车的阻抗差异，又无法通过票额分配策略引导客流.分析多停站模式下两类市郊乘客对差异化列车的乘车选择概率并分配客流，是制定满足客流需求开行方案的前提.根据两类乘客对时刻表的敏感度，分析市郊乘客乘车选择方法.

(1)不看时刻表的乘客注重乘车便捷性.该类乘客均匀到站并乘坐最近可达车次，不会在站内额外等候大站快车，列车选乘概率相同.

(2)看时刻表到站的乘客，对通勤时间敏感，会根据车次信息选择路径(车次)综合出行成本最低的方案.通常在交通分配中要考虑路径拥挤度对乘客的影响.与道路交通不同，在市郊列车容量内，乘客拥挤不影响通勤时长，因此不考虑拥挤对该部分客流的阻抗作用.多种停站模式时，第s列车对该类乘客的吸引概率可用Logit模型表示，如式(2)所示.

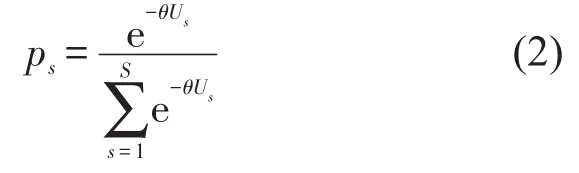
式中：θ为非负校正参数，表示乘客受列车在途时间影响改变乘车选择的意愿，通勤乘客出行时段范围较小，为节省部分在途时间而调整出行时段的可能性较低，本文取为各车次的广义出行费用，与乘车时间有关，如式(3)所示.

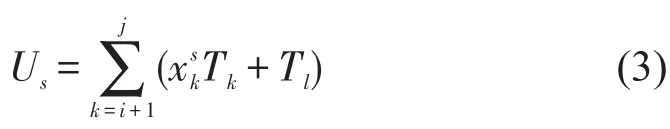
式中：Tl为区间l运行时间；为s列车在k站停时.此时乘客的选择行为即客流Qij分配方法，如图1所示.

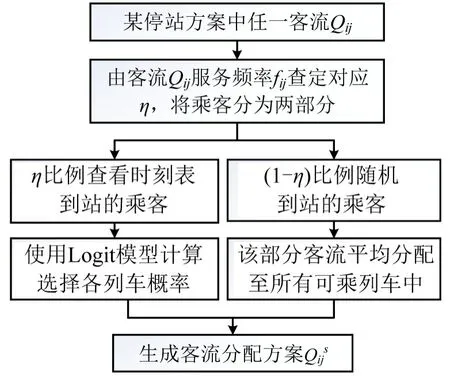
图1 客流分配流程Fig.1 Passenger flow distribution process

2 模型构建

2.1 模型假设

模型所列开行成本为相对值，固定运营成本和区间运行成本因不影响开行方案制定而不计；同时因客流方向性不均、列车可能不成对运行，本文仅针对单向客流优化开行方案.为方便建模，设定假设如下：

(1)高峰期乘客同线换乘成本较高，乘客只选择与出行相匹配的车次；

(2)列车定员和始发终到站相同.

2.2 目标函数

(1)乘客时间成本最低.

乘客时间受开行方案影响的包括在站候车和在途停站两部分.

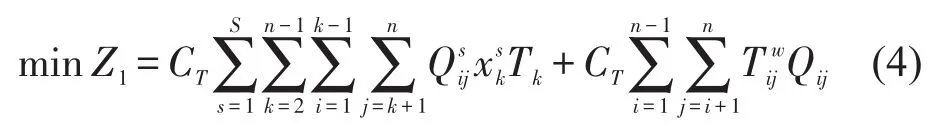
式中：CT为乘客单位时间价值(元/min)；为周期时段乘s车从i站到j站的客流量(人/h)；为决策变量，表示第s列车在k站是否停车，停车取1，不停取0；为Qij乘客的平均候车时间，如表1所示.

(2)企业运营成本最低.

企业运营成本与列车停站总次数有关，包括进出站列车每次起停电能和制动损耗等成本CE和车站接发列车单次运营费用CY.

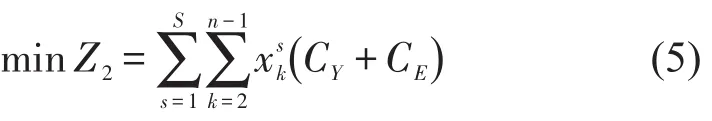
(3)企业附加成本最低.

相对于开行基本停站列车，停站方案Sp增加后，系统设备调整、运营作业协调和系统运营风险的提高等也会使企业附加成本增加CN.企业附加成本Z3为Sp的线性函数，如式(6)所示.

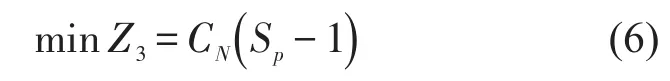
2.3 约束条件

(1)运输能力约束.

周期时段开行列数S由最大断面客流和列车设计满载率ρmax决定，如式(7)所示，D为列车定员.停站方案数量约束如式(8)所示.

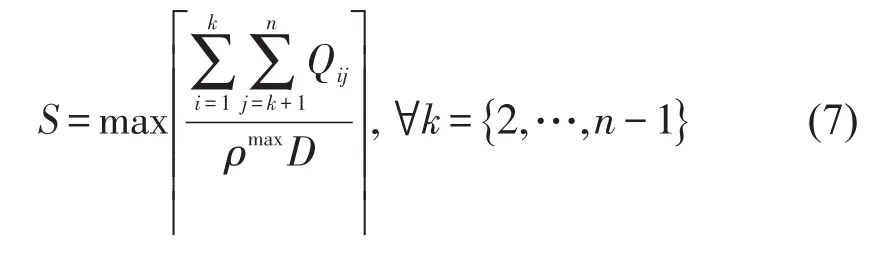
(2)客流约束.

若开行方案设计合理，则任意k区间不超载.且为保证列车运力均衡，各列车区间上座率应不低于ρmin，如式(9)和式(10)所示.

(3)服务频率约束.

为避免周期内低出行OD乘客因服务频率fij较低而候车过久，应设置周期内最低服务频率，如式(11)所示.

3 算法求解

3.1 多目标函数转化

式(4)～式(6)中各目标函数已将乘客时间与企业运营等成本去量纲化，转化为费用.本节通过线性加权的方式将各目标函数与效用函数建立关系，使多目标规划问题转化为传统的单目标规划问题并求和运算，如式(12)所示.

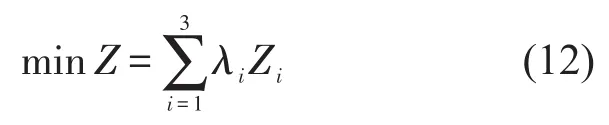
此时可根据运营公司补贴情况和当地收入水平确定各目标权重值λi，各权重和为1.

3.2 算法设计

本文非线性整数规划模型可使用遗传算法和Matlab语言编程求解，算法步骤如下：

Step 1编 码.

根据停站变量特点采用二进制方式对染色体编码.每个染色体为S行n列的0-1矩阵，列车停站记为1，不停记为0.且染色体第1、n列基因位点均取1，其他位点取随机值.

Step 2生成初始种群.

重复Step1过程popsize=150次，构成初始种群.

Step 3客流分配.

对于每个临时的停站解，按照论文1.2节方法分配客流，生成该停站方案的

Step 4适应度计算.

基于当前各解(个体)的客流分配结果，计算各方案广义开行成本，并结合约束条件评价个体适应度.引入违约惩罚系数106加入原目标g(x)=Z中，并使用映射将原问题转化为求适应度最大.适应度越大解的质量越高、开行成本越低.Zmax为原目标函数中每代最大值.

Step 5终止判定.

若迭代次数达到预设最大值300，输出当前种群中最优个体编码及目标值，编码矩阵即为最优停站方案.否则转Step6继续生成子代.

Step 6生成子代.

(1)选择.适应度最高的个体直接进入下一代，其余个体按“轮盘赌”方式抽样进入下一代.

(2)交叉.染色体两两配对，以交叉概率pc=0.7交换随机交叉点后染色体部分.

(3)变异.对每一个基因座按变异概率pm=0.1将0-1值互换.

当前代次数加1，转Step3.

4 算例分析

以某市郊铁路早高峰小时进城方向远期预测客流为例，验证本文模型算法的优化效果.该线路共11座车站，按地区收入取CT为0.5元/min；列车进站起停成本CE为100元/列；车站服务成本CY为350元/次；CRH6S市郊动车组定员1 322人.

4.1 高峰小时开行方案

高峰时期乘客对运输能力需求较高，取列车最大满载率ρmax=1，并要求ρmin=0.5；根据公共交通服务水平要求，为避免客流转移，取为4.综合考虑企业附加成本CN为3 000元/h，各目标权重值视为相同.该时段方向OD客流如表2所示.

各站客流乘降总量对比如图2所示.该市郊线路在研究时段方向以输送进城客流为主，乘客在沿途各站乘车后集中到达市区车站，客流方向性明显、站间不均衡性较大.

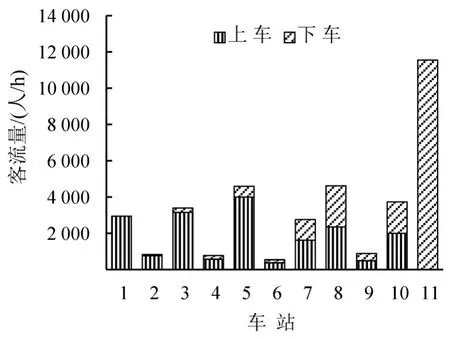
图2 各站乘降客流量对比Fig.2 Comparison of passenger traffic at each station

由算法编程得到最优开行方案如表3所示.

早高峰小时进城方向共开行10列车，包括以下3种停站类型的列车：

(1)站站停列车.

该类列车旅行时间最长.开行4列站站停列车，可服务所有出行OD的乘客，满足客流最低列车服务频率要求.

(2)跨站停快车.

该类列车在部分小站越行.开行4列跨站停快车，节省4、6、9低客流站停站运营成本，并节省在车乘客的旅行时间.

(3)大站停特快车.

该类列车只停少数大站.开行2列大站停特快车，可进一步降低停站费用、节省强OD客流的时间成本.

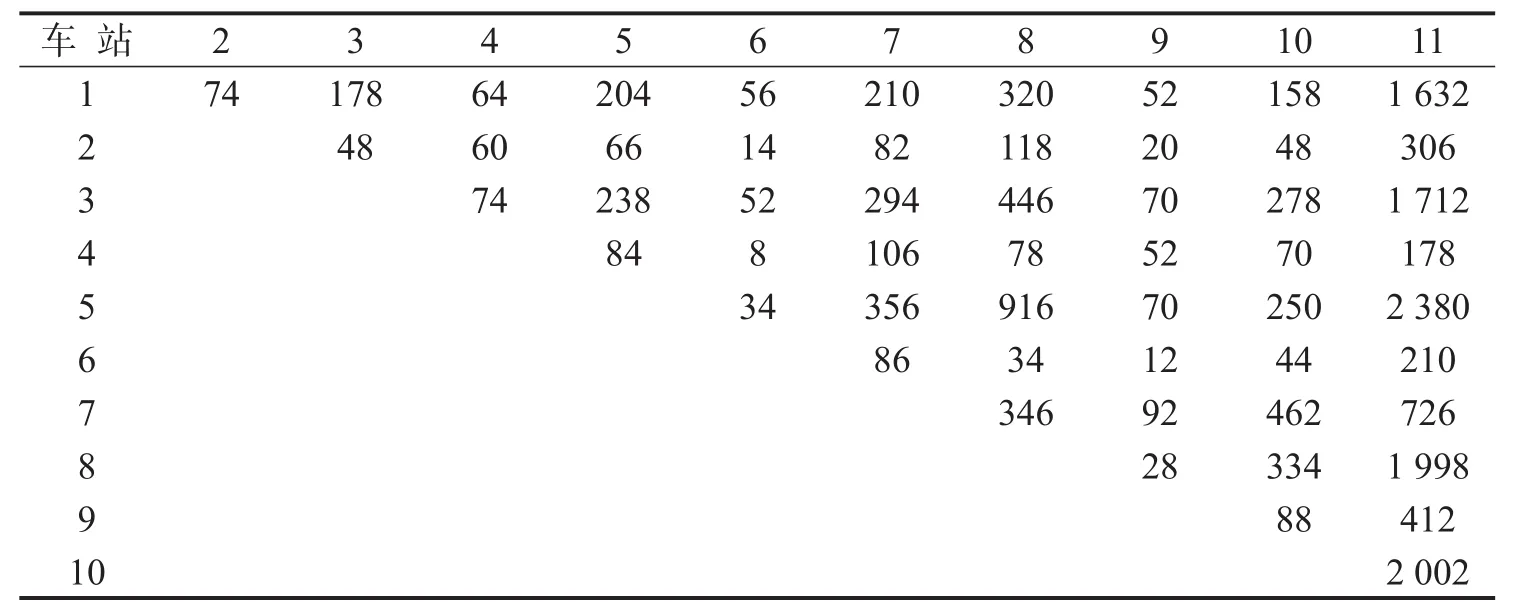
表2 高峰小时OD客流Table 2 Peak hour OD passenger flow

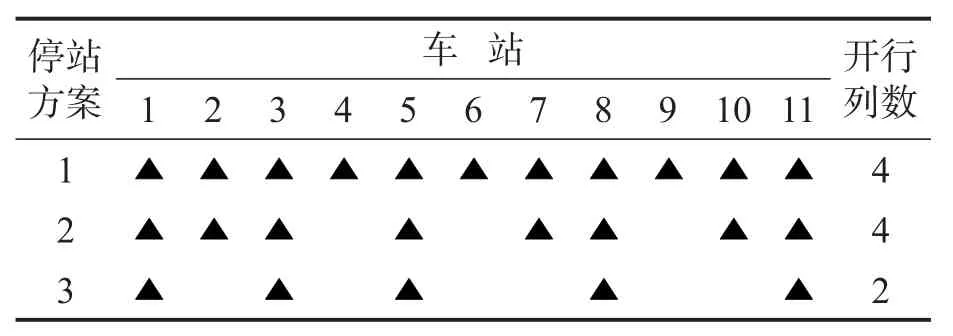
表3 高峰小时开行方案Table 3 Peak hour operation plan

4.2 与均匀到达模式对比分析

常规均匀到达模式认为乘客随机到达车站、选乘各列车概率相同，其候车时间为0.5倍发车间隔.为分析乘客到达模式对开行方案结果的影响，本节在原模型基础上，求解基于传统均匀到达模式下的最优开行方案，如表4所示.所得方案只开行两种停站模式的列车，且停站总数较少.

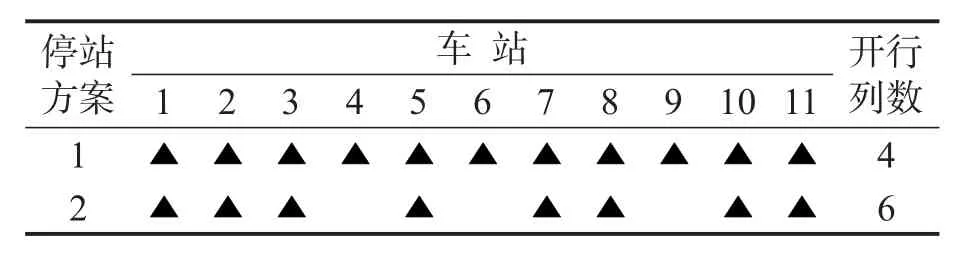
表4 按均匀到达模式所得开行方案Table 4 The opening plan based on uniform arrival mode

对比两开行方案各项成本，如图3所示.基于传统的均匀到达模式得到的开行方案因高估了乘客候车时间成本，对列车不停站通过更加谨慎，因此没有将中途停站时间成本进一步降低；列车频繁停站又产生了较高的企业运营成本，使得该方案总成本高于混合候车模式.这表明使用乘客混合到达模式制定市郊列车开行方案，通过准确描述市郊乘客的候车行为和乘车选择，定义成本构成，决策停站结果，具有更好的开行效益.

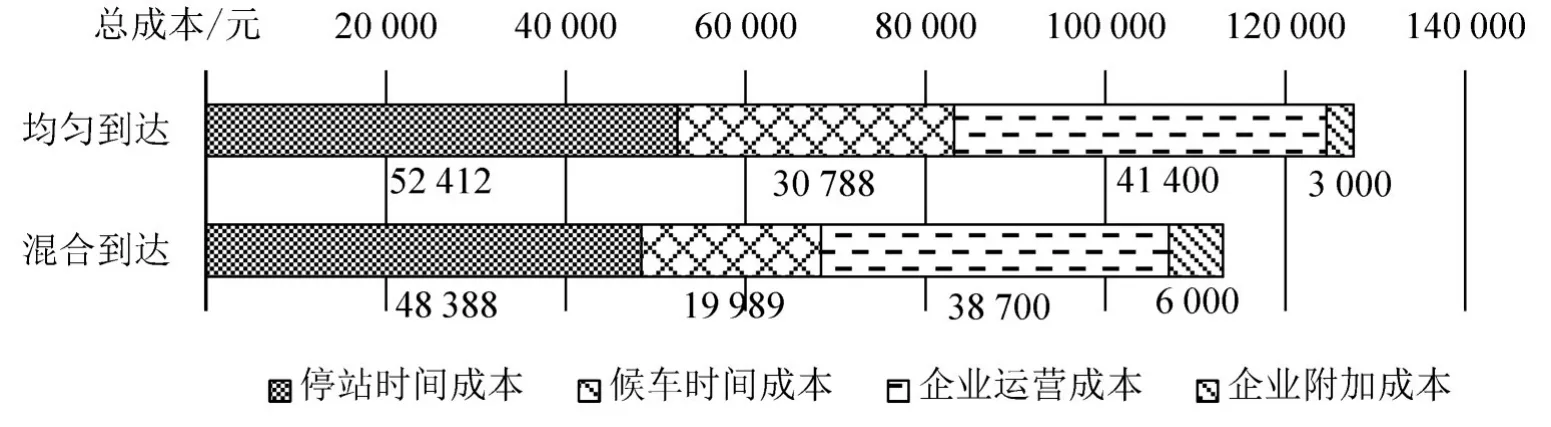
图3 考虑不同到达模式的开行方案成本对比Fig.3 Comparison of costs of operation plans considering different arrival modes

4.3 企业附加成本灵敏度分析

企业附加成本包含的项目构成较多，统计口径多样.为进一步说明不同成本对本文开行方案的影响，将CN调整至原值的0、1/3、2/3、1、2、3倍，则停站方案种类和开行总成本随企业附加成本的变化趋势如图4所示.

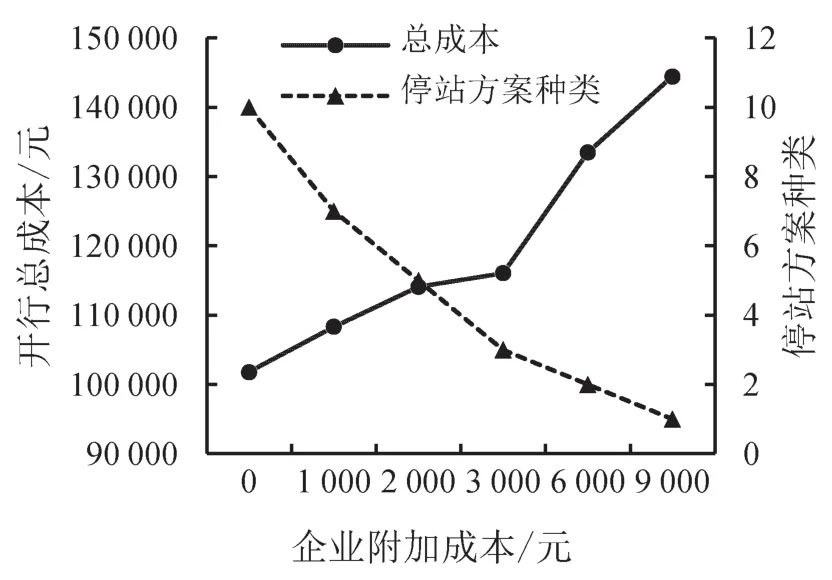
图4 企业附加成本对开行方案影响Fig.4 The impact of enterprise additional costs on the operation plan

可以看出：

(1)企业附加成本为0时，为降低开行成本而任意变更列车停站不受约束，单列车停站最优解即为全局最优解.此方案停站复杂但成本最低，在高峰小时的市郊铁路难以实施.

(2)随着企业附加成本增加，停站方案调整阈值提高，低收益停站方案被舍弃，总成本较之前提高.当达到9 000时，任何停站调整都不具备成本优势，此时只开行一种列车.此方案适用于因设备、技术原因只开行站站停列车的地铁公司.

因此，降低企业附加成本，对于降低乘客通勤成本、优化开行方案具有重要的意义.

5 结论

本文基于公布时刻表后乘客的混合到达模式，分析了多停站、公交化运营模式下乘客的乘车选择与停站方案之间的动态影响，建立了广义费用最低的停站模型，并设计遗传算法求解.通过算例分析，并与乘客均匀到达模式所得开行方案进行对比，结果表明：乘客混合到达模式对市郊铁路客流具有良好的适用性，基于该模式分配客流并设计开行方案对于节省乘客旅行时间、降低开行成本具有较好的效益.本文研究为市郊铁路列车开行方案的制定优化提供了有益的参考.