基于集成模型的多维活动—出行决策研究

付学梅，隽志才

(1.山东大学管理学院，济南250100；2.上海交通大学安泰经济与管理学院，上海200030)

0 引 言

出行需求是个体为了参与在时间和空间范围内呈离散分布的各类活动所产生的引致需求，在此基础上，活动—出行行为分析模型受到广泛关注，这种方式致力于理解并再现个体出行者的活动—出行决策过程.该决策过程涉及多个行为决策维度，远至长期内的居住地和通勤距离决策，中期的交通出行工具拥有决策；近至短期的日通勤出行方式等.为了更加全面系统的理解活动—出行决策过程及机理，为交通需求管理政策制定、实施和评价提供切实可行的依据，有必要对多维的活动—出行决策进行集成分析.

由于多维活动—出行行为分析的复杂性，国内外的大部分研究仅对一维的决策行为进行单独分析，其中出行方式结构作为衡量城市交通系统运行效率重要指标，其研究最为普遍，这种方式将其他决策维度视为外生既定变量，对各决策间的结构作用关系不予考虑.Strathman等[1]建立巢式Logit模型分析出行链结构和出行方式间的因果关系，发现出行链结构的确定优先于出行方式.Yang等[2]建立交叉巢式Logit分析居住地位置、出行方式和出行方式的联合决策；结果显示，当外部条件发生变化时，决策者倾向于首先改变出发时间，然后出行方式，最后是居住地位置.尽管这种方式从建模和估计的角度来说比较方便容易，然而它们简单地将多维活动—出行决策的制定看作一个序列过程，忽略了各决策行为的制定可能存在某种程度的同时性关系.Islam等[3]详细分析了出行链结构和出行方式之间的关系，发现对于工作日的工作出行链，出行链结构和出行方式同时被确定，这对将出行方式选择独立于其他活动—出行决策的分析方法提出了质疑.现有研究已经证实各活动—出行决策并非相互独立，而是存在着非常复杂的影响和相关关系，需要将它们作为一个“决策束”[4]，建立联合模型进行集成分析.

本文对离散—连续的活动—出行行为的5个决策维度进行联合建模分析，包括连续的通勤出行距离、离散的通勤出行方式和出发时间(无序变量)，以及离散的小汽车拥有量和日非工作活动量(有序变量)，将各决策维度间复杂的相互作用关系考虑进模型.在该模型中，所研究的5个决策维度之间不仅存在直接可见的结构影响，还被假定受到共性不可见因素的同时影响.

1 样本数据及模型变量

本文以绍兴市2013年居民出行调查数据为依托，研究个体出行者5方面的活动—出行决策；同时，决策者个人及其家庭的社会经济属性，包括性别、年龄、收入水平、教育程度、小孩、家庭人口数及交通工具数等，作为模型的外生解释变量，这种做法主要是由于：①问卷调查内容的限制，②学者们在对这5类决策进行单独研究时，已证实这些属性变量对出行者的决策有显著影响，因此，本文进一步探讨在联合模型中，决策者的社会经济属性变量对各决策维度的影响及各决策维度间的相互作用.

所选样本共包括4 602位通勤者，详细记录了每个个体的社会经济属性及其活动—出行安排.模型所涉及的变量定义如表1所示，本样本与《绍兴统计年鉴-2014》的对比结果显示，样本的性别、年龄等社会经济属性变量分布与绍兴市的整体分布间具有很大的一致性，证明了样本的代表性.

表1 模型变量定义Table 1 Definition of variables

2 多维活动—出行决策的集成模型

针对不同类型变量所采用的基础模型不同，以下将对该集成模型进行介绍.为简略起见，表示个体出行者的符号n在模型中没有给出.

用G表示无序型离散变量的数目，g为每个无序型离散变量的标识，Kg表示第g个无序型离散变量的选择肢数，kg表示第g个无序型离散变量的第kg个选择肢，第g个无序型离散变量的第kg个选择肢的效用函数为

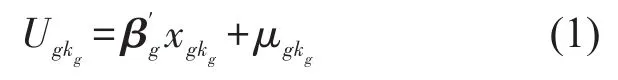
第g个无序型离散变量所有选择肢得到的误差列向量为μg=(μg1,μg2,…,μgKg)，其方差—协方差矩阵为Ωg.假定对于第g个无序型离散变量，个体出行者的选择第mg个选择肢，根据随机效用最大化理论，效用差,一定小于0，第g个无序型离散变量对应的效用差向量，并且对于每一个无序型离散变量，都需要指定一个选择肢为基准，最终只能估计（Kg-1）个选择肢，估计的选择肢总数为

用O表示有序型离散变量的数目，o为每个无序型离散变量的标识，Jo表示第o个有序型离散变量的最大值，jo=0,1,…,Jo.假定对于第o个有序型离散变量，个体出行者的选择为io，则第o个有序型离散变量的有序响应模型表达式为

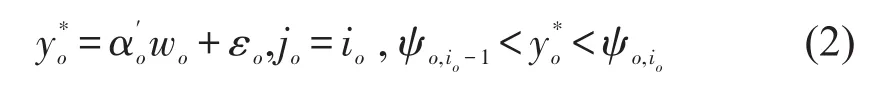
式中：wo为对应于第o个有序型离散变量的解释变量；αo为待估参数；误差项εo服从标准正态分布；ψ表示相对应的阈值.

将O个有序型离散变量排成(O×1)维的列向量y*，则，其中，是随机误差列向量ε=(ε1,ε2,…,εO)的协方差矩阵，对应的，将阈值下限及上限分别排成(O×1)维的列向量ψlow和ψup.

用C表示连续型变量的数目，c为每个连续型变量的标识，此处将其变换为对应值的自然对数.则第c个连续型变量的模型表达式为

式(3)将因变量yc表示为解释变量lc的线性回归方程，将C个连续型变量排成(C×1)维的列向量y，则y～N(c,Σy)，其中，Σy为误差项ξ=(ξ1,ξ2,…,ξC)的协方差矩阵.

在此仅对模型的构建过程进行简要介绍，可参考Paleti等[5]查看更加详细的模型.用θ表示所有待估参数的集合，则似然函数为

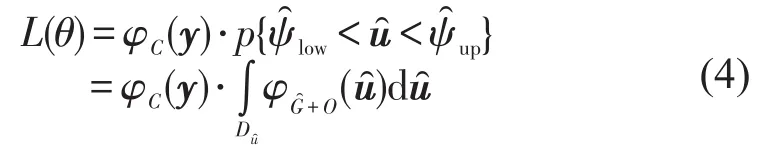
式中：̑是无序型离散变量随机效用差和有序型离散变量构成的向量，即；同样的，阈值表示为，这里-∞G̑表示的负无穷列向量表示的零列向量，这两列阈值对应的是无序型离散变量的随机效用差，阈值ψlow和ψup对应的是有序型离散变量；φC和分别是连续型变量y及离散型变量̑的概率密度函数，积分域.

可见，该似然函数包含1个G̑+O维的积分，当离散型变量或者无序型离散变量的选择肢数量较多时，要得到积分值十分困难.因此，采用Bhat[6]提出的MACML将上述似然函数进行分解，如式(5)所示.

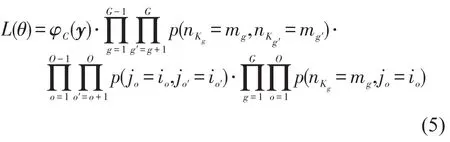
通过将原似然函数对应于离散型变量的部分分解为成对的概率值的乘积，最终的似然函数仅涉及一维及二维变量的积分.

3 模型标定及结果分析

参数标定由GAUSS软件完成，该部分给出了对5类连续—离散的活动—出行决策变量的标定结果，如表2～表4所示，表中列出在90%的置信水平下，解释变量对目标决策变量存在显著影响时，对应的参数值和T值.标定结果显示，个体的社会经济属性对他们的活动—出行决策有很重要的影响.以通勤出行方式选择为例，随着收入的增加，个体出行者选择公交车的概率降低，高收入群体更愿意选择小汽车作为通勤方式，由于他们愿意并能够负担使用私家车的高费用，以此来享受私家车带来的方便、快捷及私人空间等.简略起见，在此不对所有标定结果进行详细解释，而着重说明模型中各决策变量间的结构作用关系.

(1)作为连续型变量，通勤出行距离通常被认为是长期的决策，即一旦家庭居住地址及工作单位地址选定，通勤出行距离就被确定，在短时期内是不会发生改变的，因此模型认为该决策对其他中短期的活动—出行决策变量有影响.

(2)第1个有序型的离散变量，小汽车拥有量为中期决策，它受到连续通勤出行距离的影响，如表3所示，通勤出行距离越长，出行者家庭小汽车的拥有量越大.

(3)第2个有序型的离散变量——日非工作活动量为短期决策，受到其他多方面活动—出行决策的影响，同样如表3所示.当出行者选择公交车作为通勤方式，他们的非工作活动数量会减少；当通勤者在早高峰之前出发时，他们非工作活动的数量会增加，而若选择在早高峰时段出发，相应的非工作活动数量则会减少，主要可能是由于道路交通量的影响，早高峰时段过于拥挤，出行者根本无法进行其他活动；随着家庭小汽车拥有量的增加，通勤者非工作活动量相应增加，小汽车为出行者带来了便利和灵活；最后，通勤出行距离对非工作活动量有负面的影响.

(4)第1个无序型的离散变量——通勤出行方式，受到长期的通勤出行距离及中期的小汽车拥有量的正面影响，即当通勤者家庭拥有更多的小汽车或者通勤出行距离很长时，相对于电动车，他们选择小汽车和公交车的概率更高.一方面可能是因为电动车不适合长距离的出行，另一方面由于电动车和小汽车同属于私人交通工具，它们之间存在竞争关系，小汽车拥有量多的家庭会选择少购买或者不购买电动车.

(5)第2个无序型的离散变量——通勤出发时间，同属于短期决策，受到多方面决策行为的影响，如表2所示.随着家庭小汽车拥有量的增加，通勤者更愿意在早高峰时段及早高峰之后出发，主要是由于小汽车所带来的灵活和快捷，通勤者可以自由掌控路线和时间；相对于在早高峰之前，通勤出行距离的增加导致出行者在早高峰时段及早高峰之后出发的概率降低；当出行者选择公交车作为通勤方式时，他们在高峰之后出发的可能性更低.

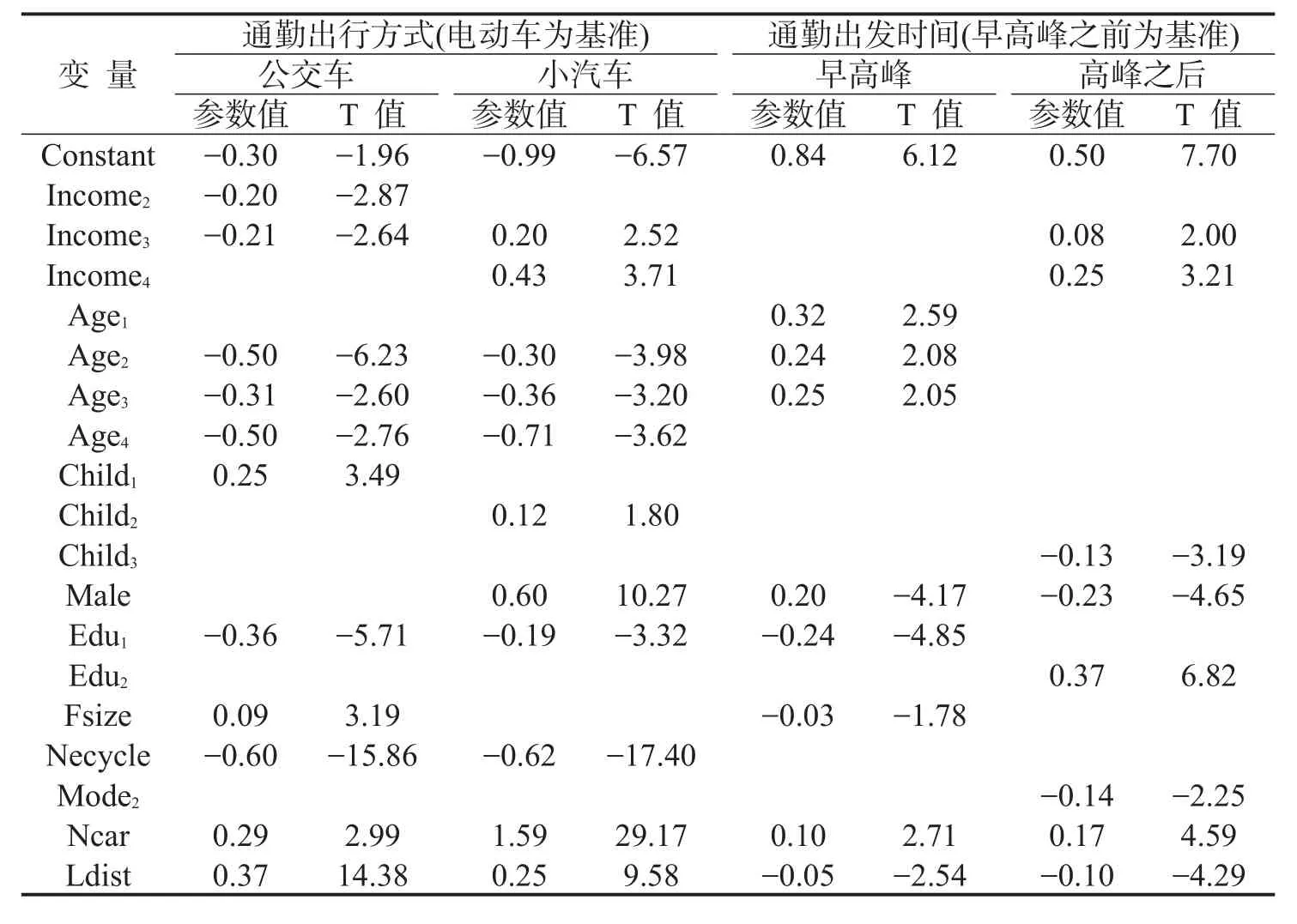
表2 模型标定结果(无序型离散变量)Table 2 Model results of nominal variables

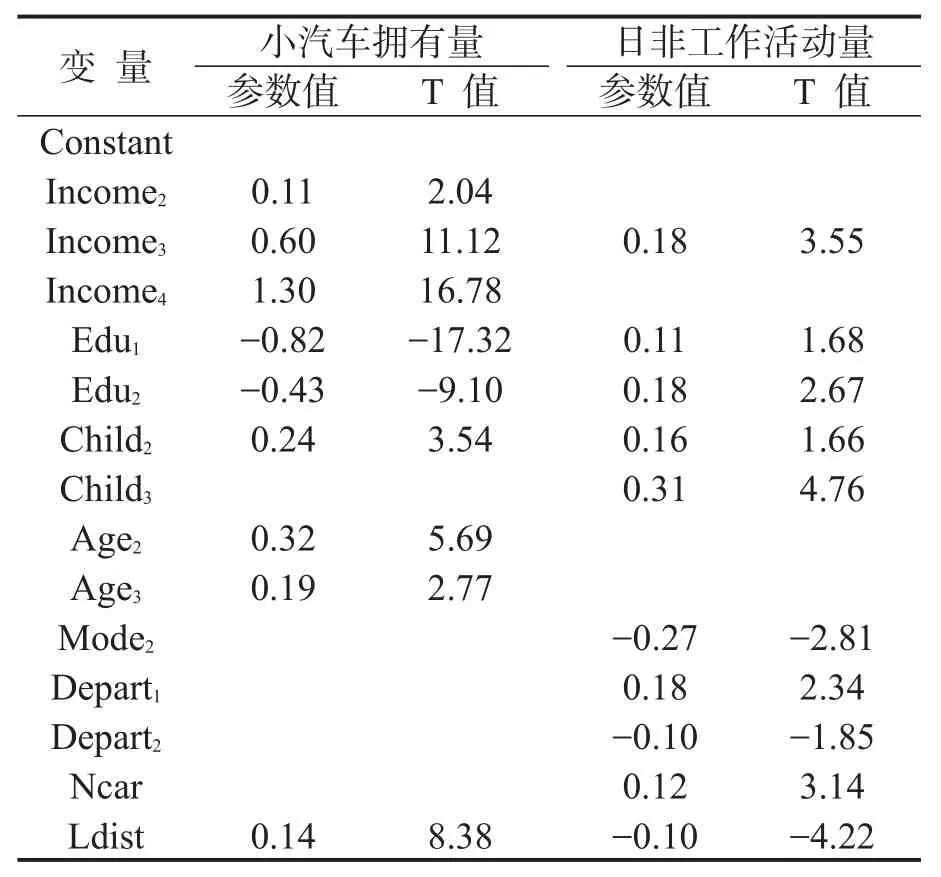
表3 模型标定结果(有序型离散变量)Table 3 Model results of ordinal variables

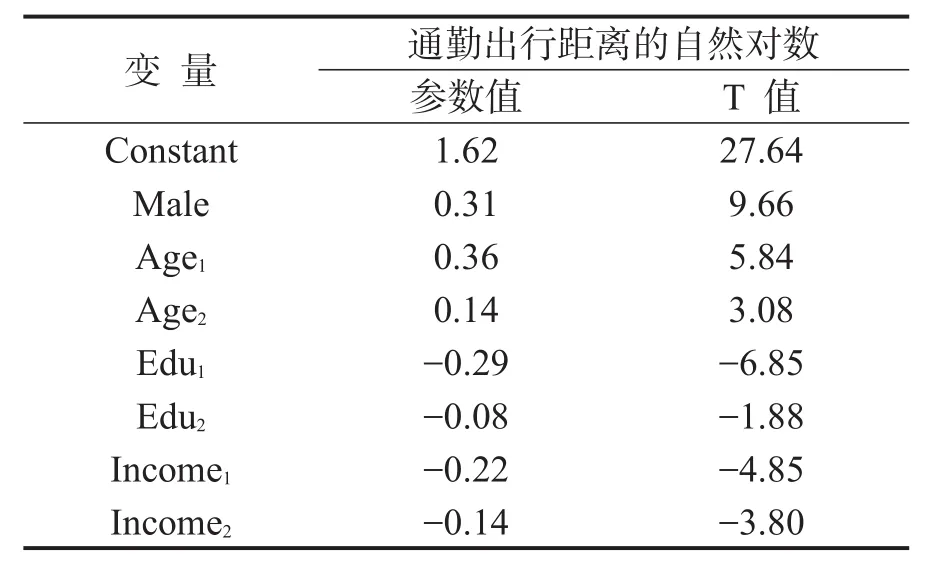
表4 模型标定结果(连续型变量)Table 4 Model results of continuous variables

除了以上所分析的多维离散—连续决策变量间的直接结构作用关系，本模型还通过非对角的协方差矩阵考虑影响这些决策变量的不可见因素间的相关关系，如表5所示.

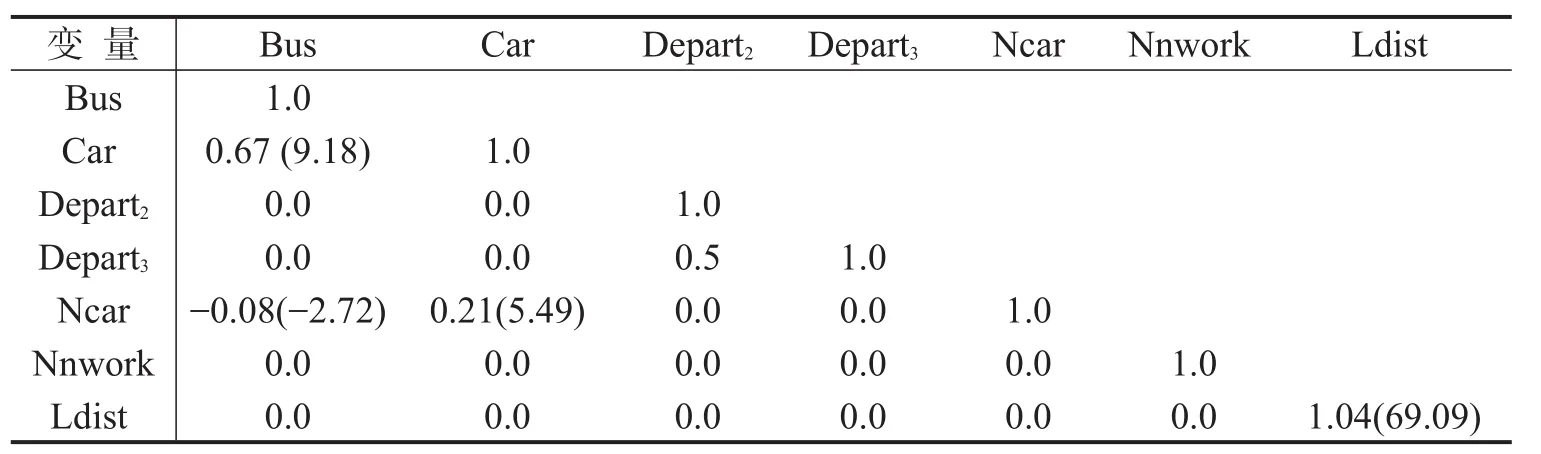
表5 各决策变量的协方差矩阵Table 5 Covariance matrix for activity-travel decisions

(1)通勤出行方式效用差间的协方差0.67表示存在共性的不可见因素同时影响公交车和小汽车的选择，可能是由于相对于电动车而言，这两种方式同属于机动化的交通工具，速度更快，出行者自身对速度的要求会同时正面影响他们对公交车和小汽车通勤出行的偏好；负的协方差-0.08表示促使出行者家庭拥有更多小汽车的不可见因素会导致该出行者更不愿意选择公交车作为通勤方式；相反地，影响小汽车拥有量的不可见因素与影响小汽车通勤的不可见因素间存在正相关关系，这表示影响出行者拥有更多小汽车的不可见因素，会促使该出行者更多地选择小汽车作为通勤方式.

(2)最终模型的log-likelihood值为-19 742.58，而不考虑各决策变量的不可见影响因素间的相关关系(即协方差矩阵为对角矩阵)的模型的loglikelihood值为-19 777.74，它们之间的似然比为70.32，在95%的置信水平下，自由度为3的卡方分布对应值为7.81，明显小于70.32，证实相对于传统的不考虑协方差矩阵的离散—连续模型，本文模型具有显著的统计优越性.

4 结 论

本文对离散—连续的5个活动—出行决策维度进行联合建模分析，一方面，模型的标定结果发现外生解释变量即个体通勤者的社会经济属性，比如年龄、性别、收入等，对所研究的5个决策维度均有很重要的影响；另一方面，这5个决策维度间的直接可见的结构作用关系，以及影响它们的不可见因素间的相关关系都证实所研究的活动—出行决策维度之间存在着密不可分的关系.

本文的研究证实了各活动—出行决策维度之间的相互影响关系，在进行行为建模的过程中，有必要考虑这种作用关系，若忽略了不同决策间的关系，会导致最终的行为模型产生偏差，这对行为研究人员及相关决策制定者都很重要的指导意义.正所谓“牵一发而动全身”，当采用政策措施或手段对某一交通需求(比如通勤距离)进行管理时，必须同时考虑该措施或手段对其他交通出行需求所产生的直接或间接的影响，确保实现系统整体最优和“幸福”最大化，而非单纯追求某一方面的改善.