前后多车影响的跟驰模型及稳定性分析
彭 勇,刘世洁,DENNIS Z Yu
(1.重庆交通大学交通运输学院,重庆400074;2.克拉克森大学商学院,波茨坦NY 13699,美国)
0 引言
车辆跟驰模型对于研究交通流特性、解决道路拥堵方面具有重要意义.随着跟驰模型的提出和发展[1-2],越来越多的学者从不同研究角度建立跟驰模型来展现交通流中诸如交通失稳、时走时停、相变等非线性特性,为解决道路交通问题提供思路和方法.袁娜等[3]提出了一种多前车速度差的跟驰模型,在线性稳定性分析中发现调节多前车信息,交通流稳定区域得到了明显扩大.杨达[4]建立了一种考虑后车的车辆跟驰模型,并在模型的基础上分析考虑后车的车辆跟驰行为特点.葛红霞等[5]引入了反馈控制信息,建立了考虑当前车与前后方车辆之间的速度差的跟驰模型,并通过线性分析得到了小扰动不致堵的条件.孙棣华等[6]考虑非相邻前车的速度差来提高道路交通流的稳定性.Yu S.等[7]提出一种前车速度差跟驰模型,通过数值模拟证实了前车的速度差异对后车的运动效果显著.以上学者在提高道路交通流稳定性方面做出了许多智慧贡献,有考虑跟驰车辆多前车影响,也有考虑跟驰车辆后车影响的跟驰模型,但是根据跟驰理论的传递特性,以及实际道路行驶经验,驾驶员会通过视野观察前后车辆的行驶状态调整自己的驾驶动作,保证跟驰车辆的甚至跟驰系统的稳定性.基于此,本文建立了一种考虑驾驶员视野内的前后多车影响的跟驰模型,对其稳定条件进行了推导和验证,并通过和经典FVD模型的对比说明了改进模型对于稳定道路交通流的优越性.
1 模型建立
1.1 跟驰模型描述
FVD(Full Velocity Difference)跟驰模型,即全速度差跟驰模型,是文献[2]提出的一种同时考虑正负速度差信息对跟驰车辆的影响,表达式为

式中:a是驾驶员反应灵敏度系数;λ是相对速度的影响因子;vn(t)是跟驰车辆n在时刻t的速度;Δvn=vn+1-vn是跟驰车辆n同前n+1车在时刻t的速度差;V(∙)是最优速度函数,即根据车头间距优化出驾驶员期望的速度.
OVD(Optimal Velocity Difference)跟驰模型,即非邻近速度差模型,是文献[6]提出的一种采用非邻近车辆的优化速度差来优化交通流的跟驰模型,表达式为
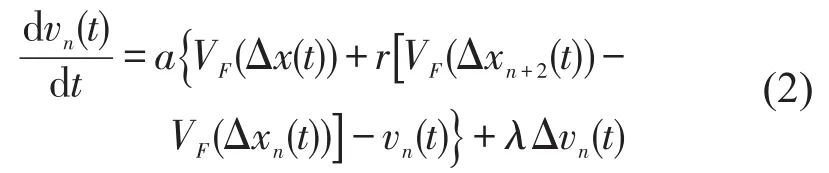
式中:r是跟驰驾驶员对非邻近车辆的关注程度,并且0≤r<0.5,当r=0时,退化为FVD 模型 ;VF(Δxn+2(t))-VF(Δxn(t))表示非邻近车辆速度差.
前车速度差跟驰模型,是文献[7]提出来的一种改进的跟驰模型,即通过考虑前导车的速度突变对道路交通流进行优化,表达式为
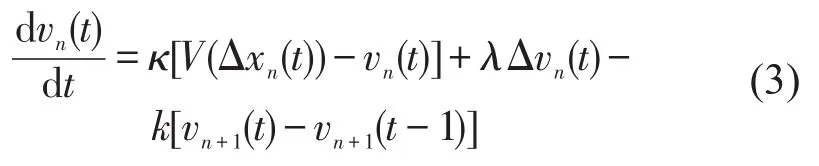
式中:κ、λ和k是敏感度系数;vn+1(t)-vn+1(t-1)是前导车的速度变化.
虽然OVD和前车速度差模型都在一定程度上对FVD模型进行改进和创新,能够较好地模拟真实交通环境中的车辆跟驰行为.但是它们无一例外地都接受了跟驰车辆只受位于它行驶方向前方的车辆影响的事实,即前导车的行驶状态影响跟驰车辆的行驶.可是在实际道路行驶中,有经验的驾驶员往往会通过视野去观察判断位于跟驰车辆前后多辆车的状态,而不是仅参考前车行驶状态.因此本文结合以上跟驰模型建立了考虑驾驶员前后多车影响的改进的跟驰模型.
1.2 考虑驾驶员前后多车影响的跟驰模型
设定车辆跟驰行驶的场景如图1所示,假定驾驶员在行驶过程中,会根据视野内的双前车及后车的状态采取加、减速的跟驰行为,来保证车辆的最优行驶状态.因为随着与跟驰车距离的变大,前方第3辆前导车对跟驰车的影响就已经很小了[8],因此本文研究仅考虑双前车和后车对跟驰行为的影响.设在某一时刻t,位于单车道上的4辆车跟驰行驶,沿车辆行驶方向的车辆编号从前到后分别是n+2、n+1、n、n-1,t时刻各车辆的位置分别为xn+2(t)、xn+1(t)、xn(t)、xn-1(t),行驶速度分别为vn+2(t)、vn+1(t)、vn(t)和vn-1(t).
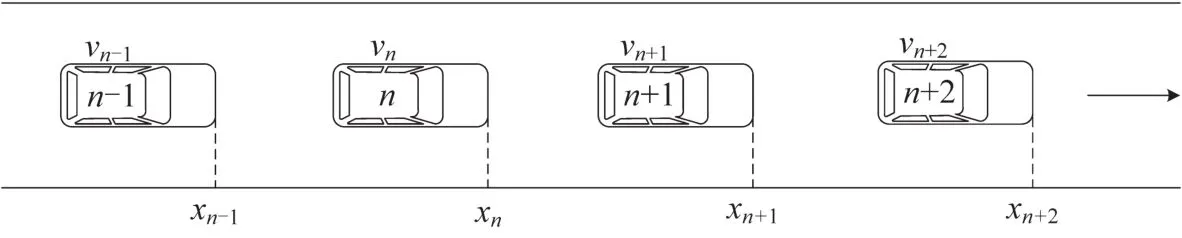
图1 跟驰场景图Fig.1 Scene graph of car-following
综合运用FVD、OVD和前车速度差模型建立的思想后,提出了新的考虑跟驰车辆双前车和后车跟驰状态对跟驰行为影响的跟驰模型为
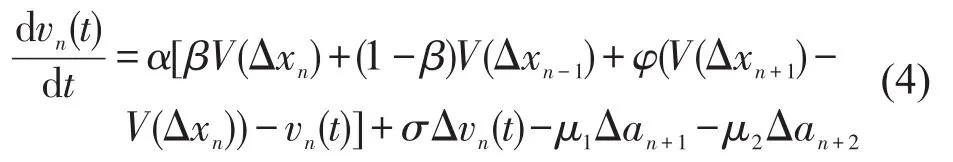
式中:α、β、φ、σ、μ1、μ2分别为灵敏度系数;V(Δxn-1)为后视野后车的最优车速;V(Δxn+1)-V(Δxn)为前视野双前车的最优速度差;Δan+1和Δan+2分别为第n+1和第n+2车在时刻t的加速度变化.当β=1,φ、μ1、μ2=0时,改进跟驰模型回归为FVD模型.
模型中采用Bando[1]提出的最优速度函数,即
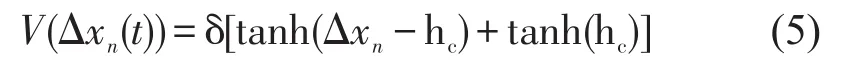
式中:δ为常数项系数,取δ=1;hc为安全距离,取hc=5.
2 稳定性分析
系统稳定性是指系统在受到瞬时扰动后,当干扰消除后能够自行恢复到原来状态的能力.在利用稳定理论分析改进模型前,首先定义道路上车辆的初始稳定状态为:所有车辆均以车头间距h0和速度V(h0)保持稳定的匀速运动.此时关于第n辆车的位置就可以表示为
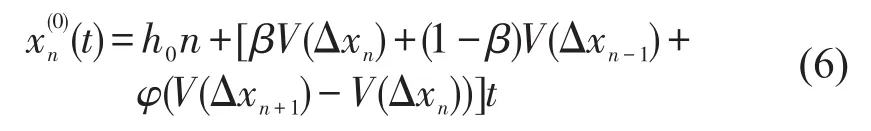
如果此时给整个系统施加一个小扰动yn(t)=eikn+θt,关于第n辆车的位置就会变化为
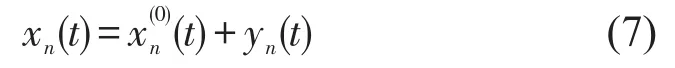
将式(6)代入式(7)中,得到
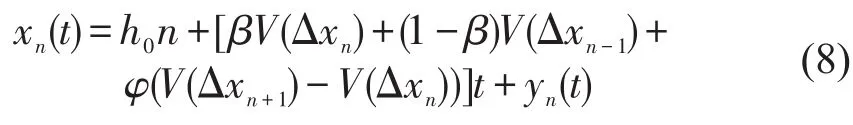
再将式(7)代入式(8)中,就得到了关于扰动yn(t)的改进模型表达式,即
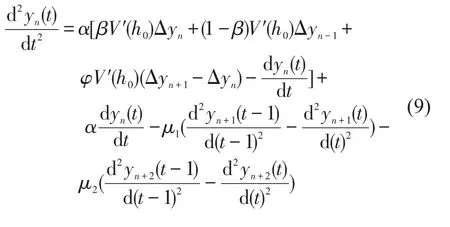
式中:V′(h0)为V(x)在x=h0处的导数.
将yn(t)=eikn+θt代入式(9)中,整理后得到关于θ的二元一次方程为
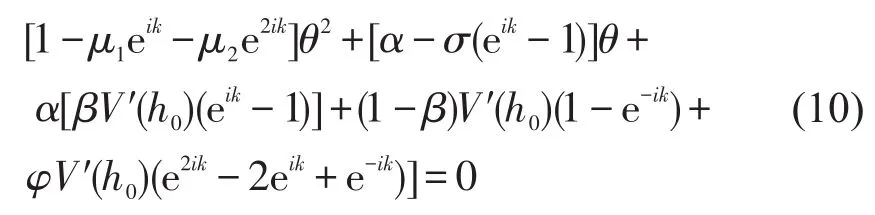
将θ展开为,代入式(10)中,得到
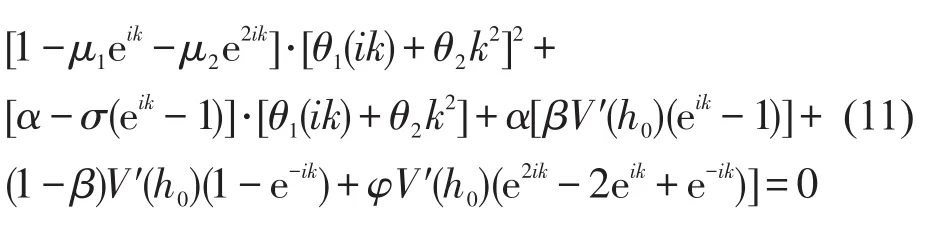
对式(11)进行整理并得到关于k的全部项为
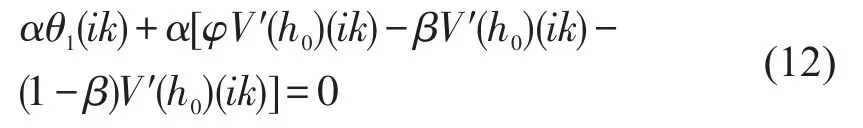
整理化简式(12)后,得到关于θ1的表达式为
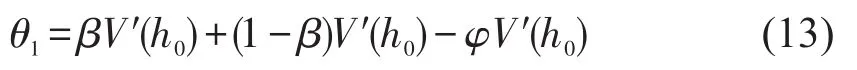
再对式(11)进行整理得到关于k2的全部项为
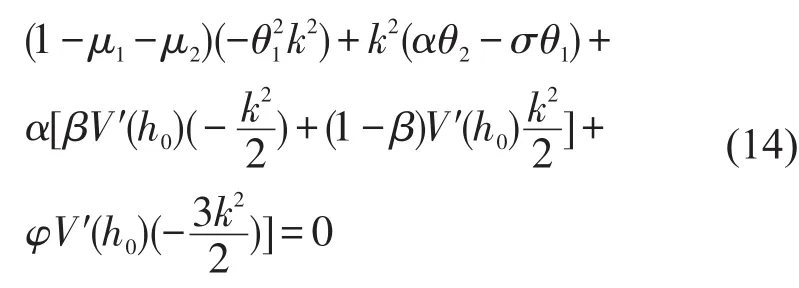
整理化简式(14)后,得到关于θ2的表达式为
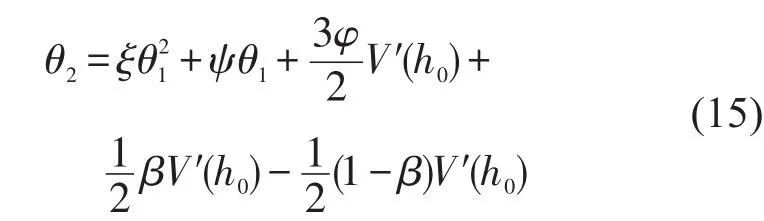
将式(13)代入式(15)中,化简得到
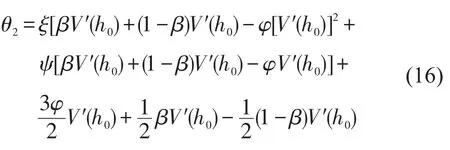
根据稳定性原理,当θ2>0时,交通系统处于稳定状态,可以抵抗干扰;反之系统将变得不稳定,任何小的干扰都可以扰乱交通系统的运行,即系统的稳定状态为
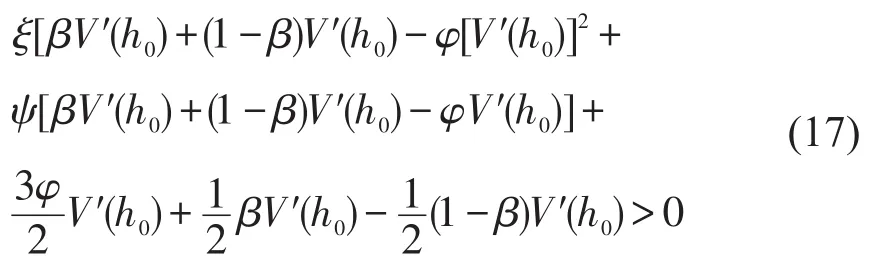
所以模型中的稳定条件为
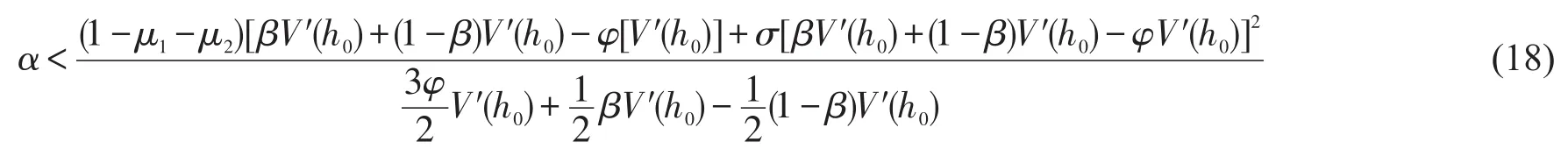
当μ1=μ2=0.5,φ=0时
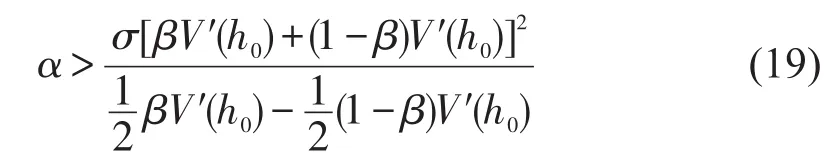
由此得到的稳定性条件式(19)满足文献[4]提出的考虑后车跟驰模型的稳定性通式,从而也验证了文本提出的跟驰交通模型的准确性.
当β=1时,得到σ不同取值下的中位稳定线,如图2所示.由图2可以看出,中位稳定线呈现对称分布,且随着σ的不断增大,中位稳定线下方的不稳定区域越来越小,上方的稳定性区域也就越来越大.同时灵敏度α的增大也随着σ增大,对于相同的跟驰间距,加速度越大越有利提高系统的稳定性,能够反映出车辆的加速性能对抑制交通拥堵的有利作用,是符合实际的.说明考虑前后车辆跟驰状态对整个跟驰系统来说是有意义的,能在一定程度上维持道路交通系统的稳定.
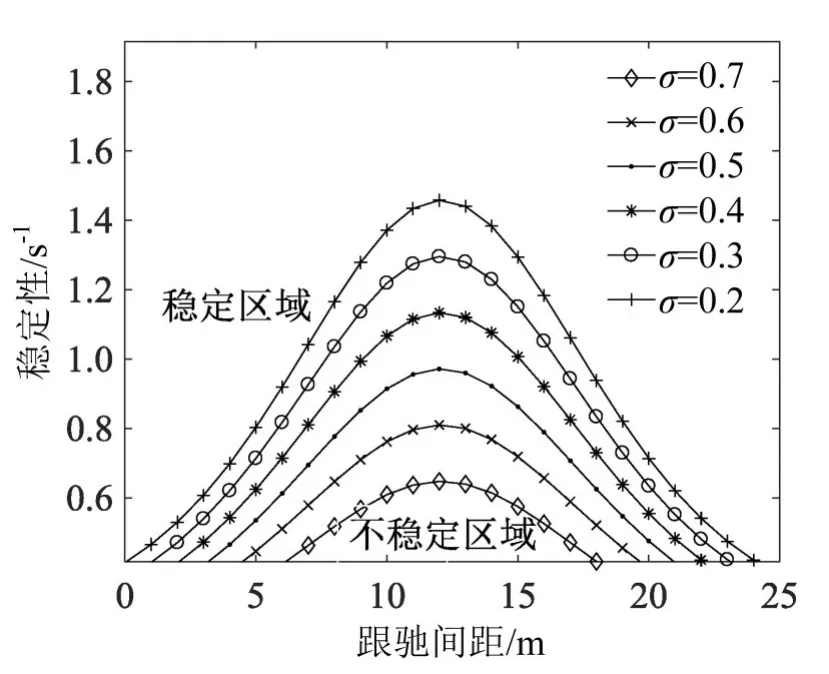
图2 不同灵敏度σ的中位稳定线图Fig.2 Medium stable line with different sensitivity
根据FVD稳定性条件:α=2V′(h0)-2ε,分别在σ=0.5和ε=0.2处得到改进模型同FVD模型的稳定性对比图,如图3所示.不难看出,改进模型较FVD模型具有更大的稳定性区间,但是在x轴两端的位置,改进模型的稳定性弱于FVD模型,这是因为FVD模型只考虑了前车跟驰状态对跟驰行为的影响,因此无论跟驰距离如何变化,跟驰系统的稳定性受车头间距的影响都是一定的.而改进模型由于考虑前后多辆车的跟驰状态,会过多地改变自身车辆的跟驰状态,影响系统的稳定性.因此,改进模型在跟驰间距处于7~18 m时,采用改进跟驰模型要比经典FVD模型更具有稳定性.
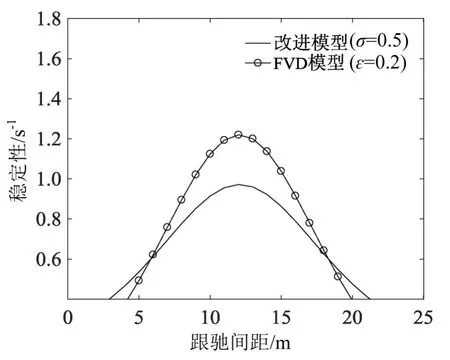
图3 中位稳定线对比图Fig.3 Comparison diagram of median stability line
3 数值仿真
通过对道路交通中的交通波现象进行模拟,观察波动的产生和消散,能够从现实角度来验证以上理论推导结论.为了更直观地探讨本文提出模型的稳定性,本文假设交通流均为同质均衡状态,即道路上的车辆全部遵循一种跟驰行驶方式,且无换道、信号灯等其他交通因素的干扰,研究在这种平衡状态下采用两种不同跟驰策略的交通流系统的稳定性.
3.1 扰动在两种模型中的传播分析
设置的模拟场景为:在一段长度L=5 000m的道路上,在道路前端L1=200m处放置N=100辆车,在初始状态,所有车辆等距离、等速度跟驰前车行驶,跟驰距离为L1/N,跟驰速度为5 m/s,采取周期边界.在仿真时间的第1 s对头车施加一个小的扰动,扰动大小为其初始跟驰间距和初始速度的1/2.
图4(a)和图4(b)分别为α=0.520;β=0.246;φ=0.013;σ=0.040;μ1=0.259;μ2=0.032时改进模型中扰动在仿真时间第200 s和第5 000 s时的传播情况.系统的平均速度稳定在0.054 m/s左右,但是由于头车的扰动打破了整个交通系统的平衡,使得系统中产生交通波动并随行驶时间向后传播,传播方向同车队行驶方向相反.且随着行驶时间的增加,扰动产生的速度波动峰值0.063 m/s变化到0.055 m/s,扰动整体有减小并消散的趋势.因为改进模型考虑了前后多车跟驰状态并提供给驾驶员做参考,使其可以更全面的对跟驰行为进行调整,以适应整个跟驰系统,能够及时调整跟驰行为应对车流中的小扰动,从而也有利于及时消散跟驰系统中的扰动,避免形成局部拥堵影响道路交通.
图4(c)和图4(d)为两种模型在仿真时间分别为T=200s和T=5 000 s时的扰动传播的对比图,FVD模型的参数选择为a=0.132,λ=0.036.可以明显看到改进模型中交通流平均速度稳定在0.05 m/s左右,而FVD模型中的跟驰系统则受扰动影响较大,系统中车辆速度一直在0~2 m/s震荡,出现了时走时停的停滞现象,且随着仿真时间的增加,扰动并没有出现消散的迹象,说明FVD模型中系统受车辆随机扰动的影响严重,因此改进模型较FVD模型在消散扰动方面具有一定优越性.
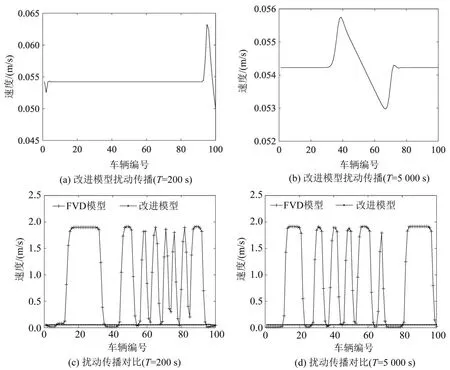
图4 扰动传播过程中系统平均速度Fig.4 Average velocity in disturbance propagation process
图5(a)和图5(b)分别为改进模型中扰动在仿真时间第200 s和第5 000 s时的跟驰距离变化情况.整个跟驰系统的跟驰间距稳定在2 m左右,由于初始小扰动产生的冲击波在三维面上有明显的起伏波动(图5(a)),后冲击波慢慢消散(图5(b)),三维面又重新渐渐恢复平整,说明改进模型模拟的交通流具有稳定性,拥有自行消散系统中冲击波的能力.反观FVD模型在扰动下的跟驰间距,如图5(c)和图5(d)所示,扰动在系统中产生的交通波并没有随时间消散,反而愈演愈烈,到了T=5 000s时已经形成了严重的交通拥堵,使得系统中的车辆不得不时走时停.因此,应用改进模型的交通系统比应用FVD模型的交通系统更具有稳定性.
图6(a)和图6(b)分别为改进模型中扰动在仿真时间第200 s和第5 000 s时的道路上所有跟驰车辆的轨迹运行图.从局部产生拥堵(图6(a)),到轨迹面又基本保持平整(图6(b)),同样说明改进模型的稳定性.而FVD模型中的交通系统在扰动的作用下,车辆轨迹图出现了多处褶皱带(图6(c)),说明系统中的车辆在运动过程中出现了多次速度为零的长时间停车现象,并向行驶方向的反方向传递,最后随着时间演化为大的拥堵节点(图6(d)).因此也就说明了FVD模型下的跟驰系统较改进模型相比缺乏自身稳定性,对系统中出现的小干扰的消散能力不足.
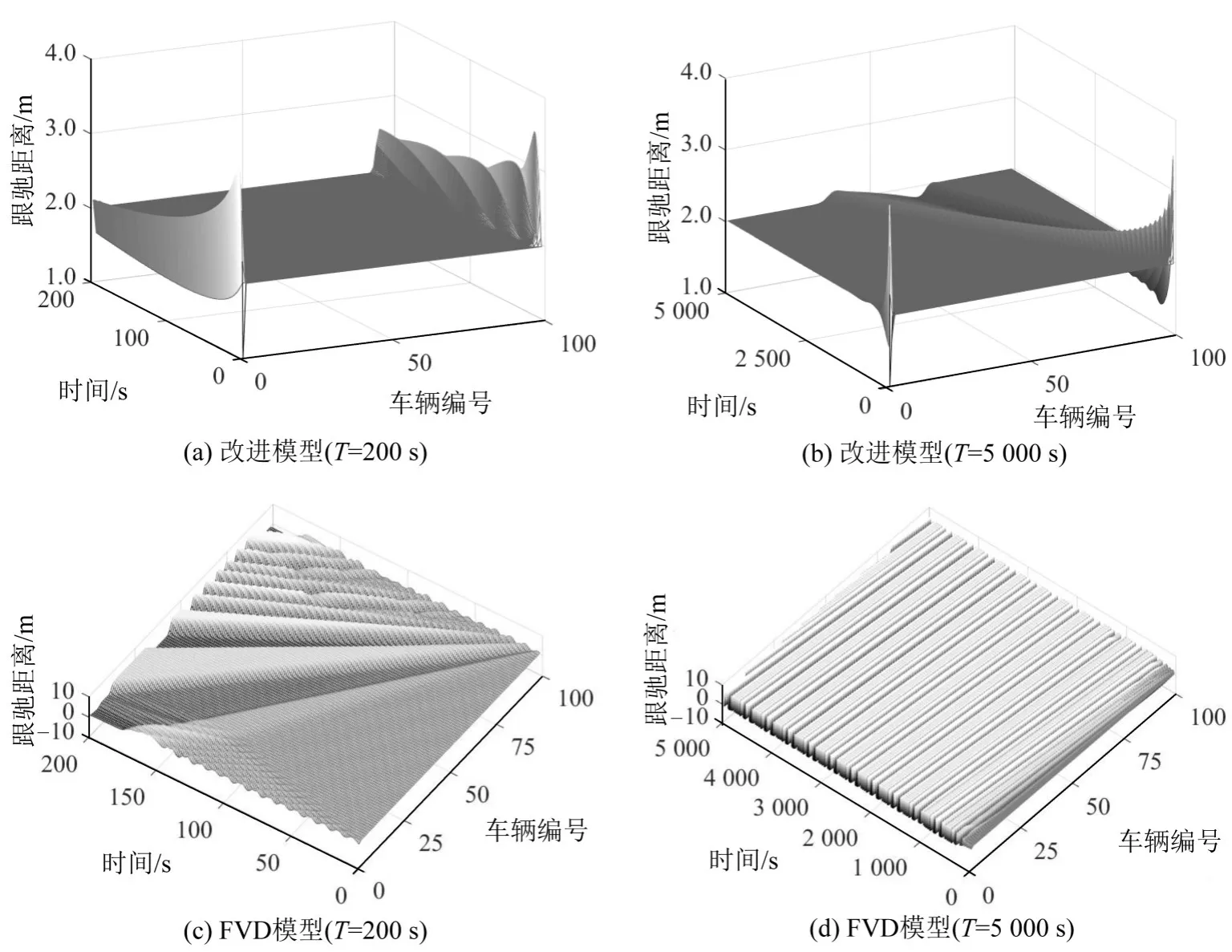
图5 扰动传播过程中系统跟驰间距Fig.5 Headway in disturbance propagation process
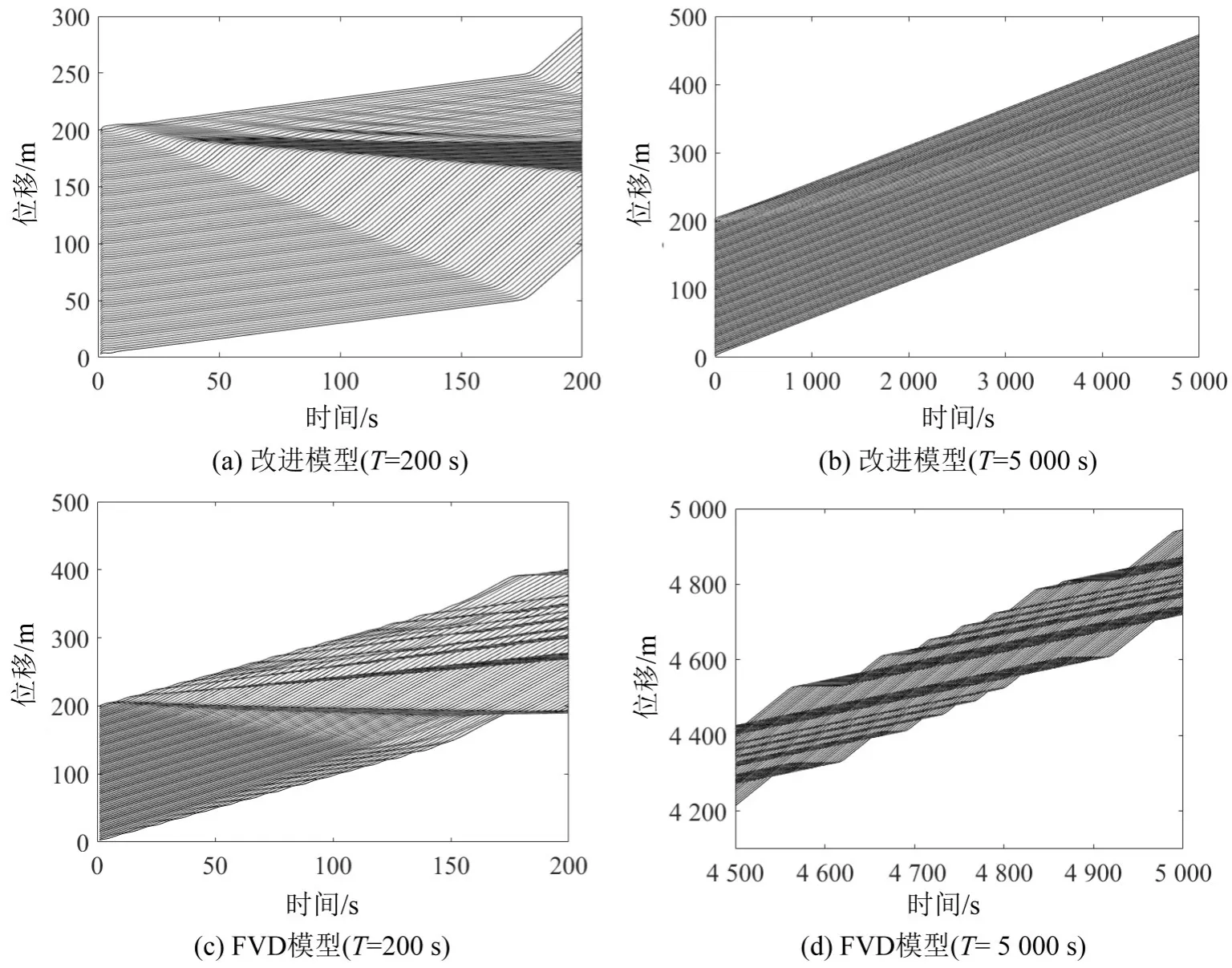
图6 扰动传播过程中的跟驰位移Fig.6 Position in disturbance propagation process
3.2 灵敏度仿真验证
为了验证第2节稳定性条件理论推导的敏感度分析结果,调整灵敏度σ的取值,并分别在仿真时间为T=50s和T=1 000s时固定观察扰动在不同灵敏度σ值下的传播情况,为了更直观地观察稳定性效果,灵敏度σ的取值同第2节保持一致,分别为σ=0.2,0.3,0.4,0.5,0.6,0.7,如图7所示.不难看出,灵敏度σ的取值越大,扰动在跟驰系统中的传播越稳定,这同3.2节中得到的理论分析结果是一致的.同时随着仿真时间的增加,只有灵敏度σ=0.2的系统中存在扰动,其他敏感度取值下的系统扰动已经完全消散,跟驰系统中的速度不再波动,而是保持稳定的一致.
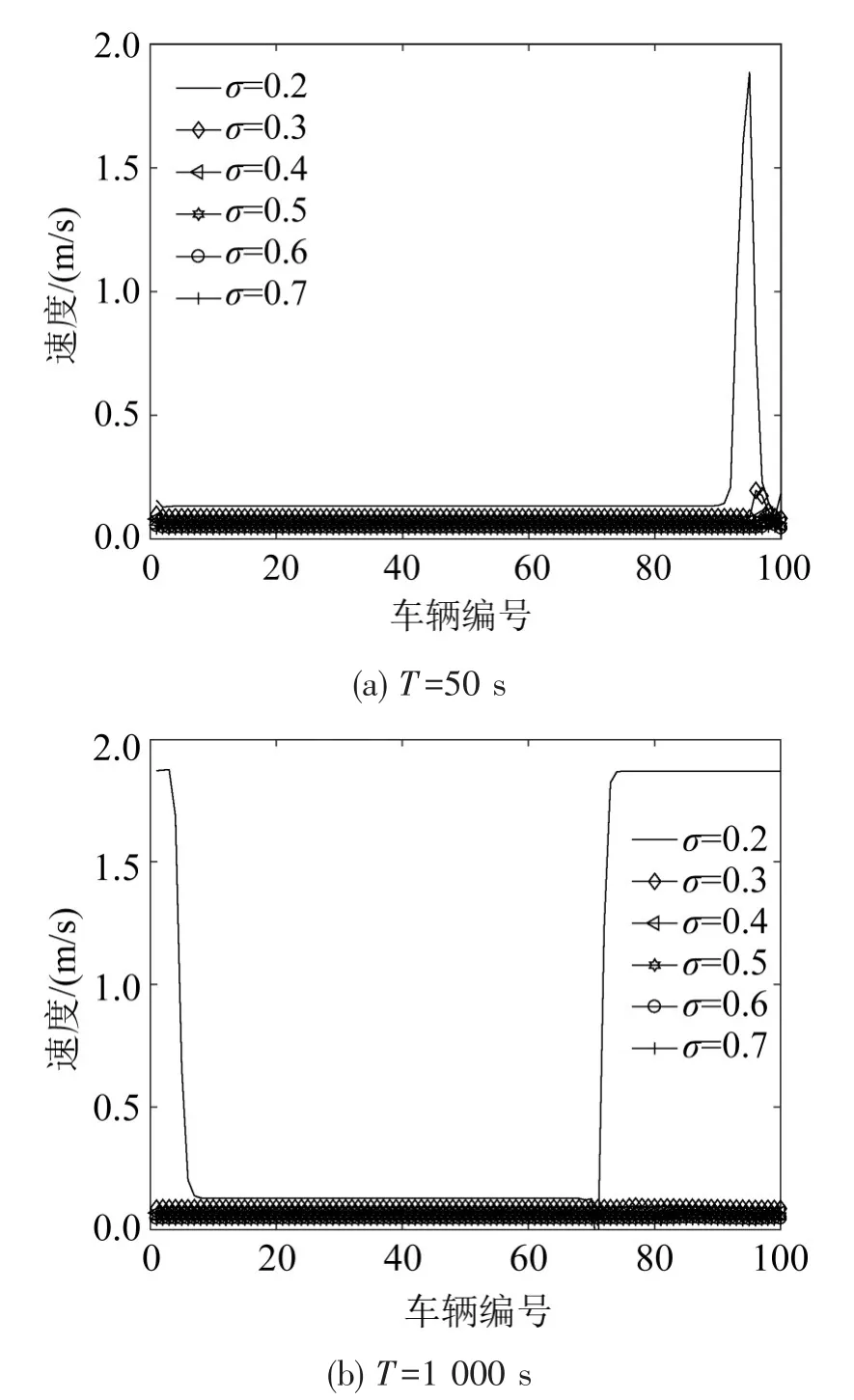
图7 不同灵敏度σ下的扰动传播速度图Fig.7 Average velocity in disturbance propagation process with different sensitivities
4 结论
本文在参考现有跟驰模型的基础上,建立了一种考虑跟驰驾驶员双前车及后车跟驰状态影响的改进跟驰模型.并从理论分析、数值仿真、对比分析等角度,对本文提出的改进模型进行分析.主要有以下结论:
(1)根据稳定性理论分析、推导了改进模型的稳定性条件,并对其进行了灵敏度验证,验证结果显示,灵敏度α越大越有利于提高系统的稳定性.
(2)模拟扰动在交通系统中传播的仿真结果显示,无论从系统跟驰速度、跟驰间距还是跟驰轨迹都能说明,改进模型都具有消散干扰抑制拥堵的作用.
(3)对比观察了经典FVD模型下的跟驰系统对抗干扰能力,对比结果显示,应用改进模型进行道路交通仿真会获得更佳的稳定性.

