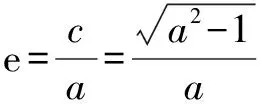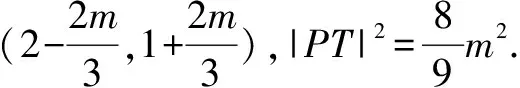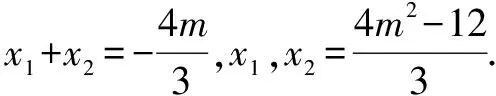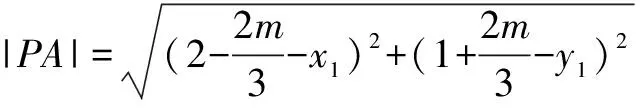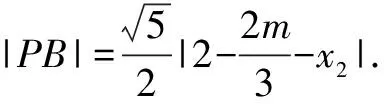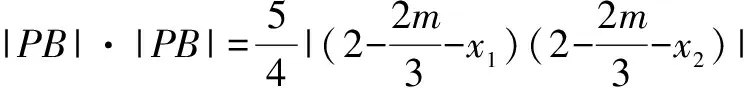圆锥曲线高考题型分析
崔 文 侯宇虹
(1.山东省文登第一中学 264400;2.山东省威海市南海高级中学 264400)
圆锥曲线是高考必考考点,备考时兼顾基础与应用,循序渐进,提升解题能力.
一、考查圆锥曲线的定义与性质
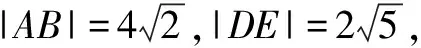
A.2 B.4 C.6 D.8
分析 设抛物线方程为y2=2px(p>0),圆的半径为r,然后计算得出p的值.
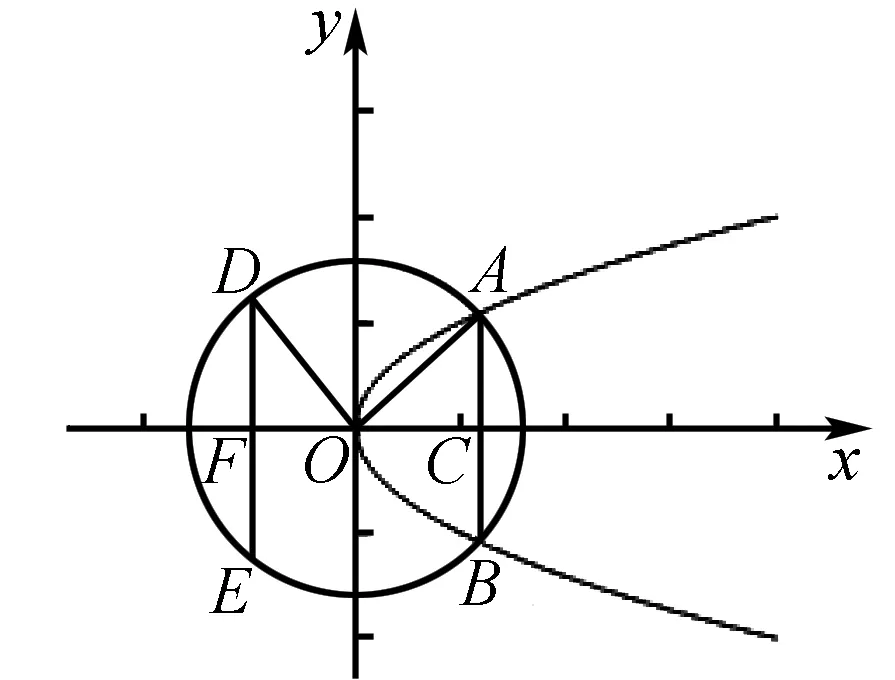
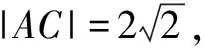
评注 把抽象的问题具体化是解决此类的问题的最佳方法.
A.m>n且e1e2>1 B.m>n且e1e2<1
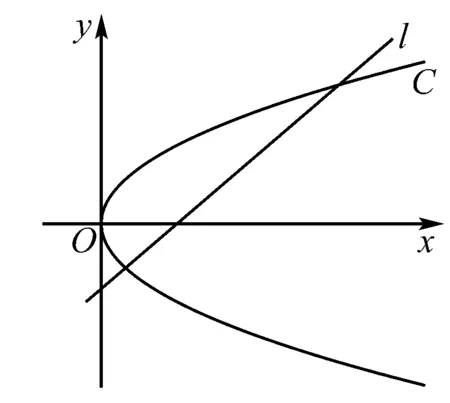
C.m 分析 根据焦点重合,可知C1、C2焦距相等,得出m与n之间的关系;然后分别写出e1与e2,分析e1e2与1的大小关系. 评注 圆锥曲线的性质侧重考查基本量a、b、c的关系,椭圆中有a2=b2+c2,双曲线中有c2=a2+b2,不要记错.基本量考查渗透在每个题目当中. 评注 离心率是高考的一个热点题型,多与其它知识点结合考查,备考时要格外关注.新课标Ⅰ卷理第5题,新课标Ⅲ卷理第11题、文第12题,浙江卷理第7题,山东卷理第13题、文第14题,都是考查离心率. 例5 已知抛物线C:y2=2x的焦点为F,平行于x轴的两条直线l1,l2分别交C于A,B两点,交C的准线于P,Q两点. (1)若F在线段AB上,R是PQ的中点,证明:AR∥FQ; (2)若△PQF的面积是△ABF的面积的两倍,求AB中点的轨迹方程. 分析 (1)证明AR与FQ的斜率相等即可;(2)首先表示出△PQF和△ABF的面积,得出一个关系式,在此基础上进行后续研究. 记过A,B两点的直线为l,则l的方程为2x-(a+b)y+ab=0. (1)由于F在线段AB上,故1+ab=0. 记AR的斜率为k1,FQ的斜率为k2,则 所以AR∥FQ. (2)设l与x轴的交点为D(x1,0), 设满足条件的AB的中点为E(x,y). 当AB与x轴垂直时,E与D重合. 所以,所求轨迹方程为y2=x-1. 评注 本题的难点在于正确的表示出△PQF和△ABF的面积,得出D点的横坐标为1.本例属于直接法求轨迹方程.新课标Ⅰ卷理第20题(Ⅰ)为定义法求轨迹方程. (1)求椭圆C的方程; (2)设P的椭圆C上一点,直线PA与y轴交于点M,直线PB与x轴交于点N,求证:|AN|·|BM|为定值. (2)由(1)知,A(2,0),B(0,1), 当x0=0时,y0=-1,|BM|=2,|AN|=2, 所以|AN|·|BM|=4. 综上,|AN|·|BM|为定值. 评注 定值(定点、定直线)问题是高考的常见题型,大多涉及直线和圆锥曲线的位置关系,对运算能力要求较高.新课标Ⅰ卷文第20题(Ⅰ),北京卷文第19题,江苏卷第22题(Ⅱ)(ⅰ),四川卷文第20题(Ⅱ),山东卷文第21题(Ⅱ)(ⅰ),均属于定值(定点、定直线)问题. (1)当t=4,|AM|=|AN|时,求△AMN的面积; (2)当2|AM|=|AN|时,求k的取值范围. 分析 (1)由|AM|=|AN|,可求出k=1,求出面积即可;(2)分别表示出|AM|和|AN|的长度,然后根据2|AM|=|AN|,得出关系式. 因为|AM|=|AN|,k>0, 4k2-k+4=0无实根,所以k=1. 因为2|AM|=|AN|, 例8 如图,在平面直角坐标系xOy中,已知直线l:x-y-2=0,抛物线C:y2=2px(p>0). (1)若直线l过抛物线C的焦点,求抛物线C的方程; (2)已知抛物线C上存在关于直线l对称的相异两点P和Q, ①求证:线段PQ的中点坐标为(2-p,-p); ②求p的取值范围. 分析 (1)由直线l过抛物线C的焦点,可知焦点坐标,得出抛物线的方程;(2)①因为点P和Q关于直线l对称,可设其方程为y=-x+b.联立y2=8x与y=-x+b,得出中点坐标,同时中点也在直线l上,得PQ的中点坐标为(2-p,-p).②由p+2b>0可得. 所以抛物线C的方程为y2=8x. (2)设P(x1,y1),Q(x2,y2),线段PQ的中点M(x0,y0). 因为点P和Q关于直线l对称,所以直线l垂直平分线段PQ,于是直线PQ的斜率为-1,则可设其方程为y=-x+b. 因为P和Q是抛物线C上的相异两点,所以y1≠y2,从而Δ=(2p)2-4(-2pb)>0,化简得p+2b>0. 因为M(x0,y0)在直线l上,所以x0=2-p. 因此,线段PQ的中点坐标为(2-p,-p). ②因为M(2-p,-p)在直线y=-x+b上, 所以-p=-(2-p)+b,即b=2-2p. 评注 对称问题关键是利用斜率乘积等于-1设出对称点所在直线的方程,然后求解.解答时必须注意判别式Δ>0. (1)求直线y=kx+1被椭圆截得的线段长(用a、k表示); (2)若任意以点A(0,1)为圆心的圆与椭圆至多有3个公共点,求椭圆离心率的取值范围. 分析 (1)利用弦长公式可得;(2)假设圆与椭圆的公共点有4个,由对称性可设y轴左侧的椭圆上有两个不同的点P,Q,满足|AP|=|AQ|,得出a的取值范围.正难则反解决问题. (2)假设圆与椭圆的公共点有4个,由对称性可设y轴左侧的椭圆上有两个不同的点P,Q,满足|AP|=|AQ|. 记直线AP,AQ的斜率分别为k1,k2,且k1,k2>0,k1≠k2. 由于k1≠k2,k1,k2>0得 评注 本题采用正难则反的思想.原来探讨“圆与椭圆至多有3个公共点”,而我们知道圆与椭圆最多有4个公共点,所以先研究4个公共点时a的取值范围,然后求补集即可.新课标Ⅰ卷文第20题(Ⅱ)也是存在性问题. 八、证明类比得到的结论 (1)求椭圆E的方程及点T的坐标; (2)设O是坐标原点,直线l′平行于OT,与椭圆E交于不同的两点A、B,且与直线l交于点P.证明:存在常数λ,使得∣PT∣2=λ∣PA∣· ∣PB∣,并求λ的值. 方程①的判别式为Δ=24(b2-3),由Δ=0,得b2=3. 此时方程①的解为x=2. 点T坐标为(2,1). 设点A,B的坐标分别为A(x1,y1),B(x2,y2). 评注 本例是类比圆中的切割线定理得出的一个结论.四川卷文科第20题是类比圆中的相交弦定理得出的一个结论.此两题成为2016年高考圆锥曲线解答题的一个亮点. 圆锥曲线因其具有丰富的性质,而备受高考命题专家青睐.圆锥曲线问题也是对数形结合能力、运算能力、逻辑分析能力的综合考查,理清命题规律,方可运筹帷幄.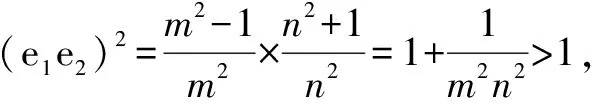
二、考查离心率
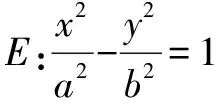
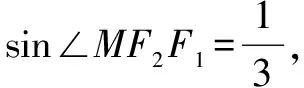
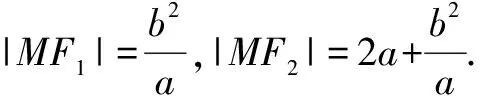
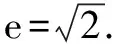
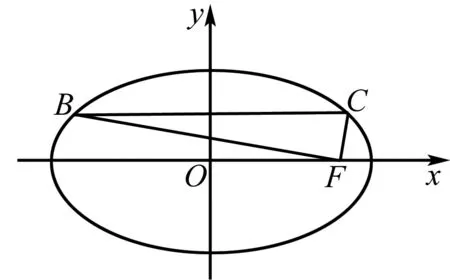
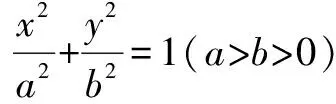
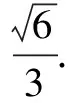
三、考查轨迹方程
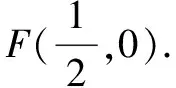
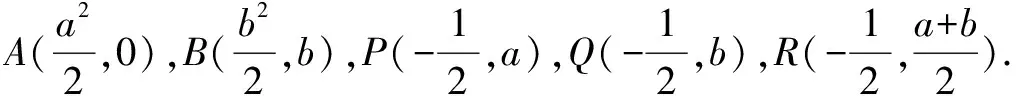
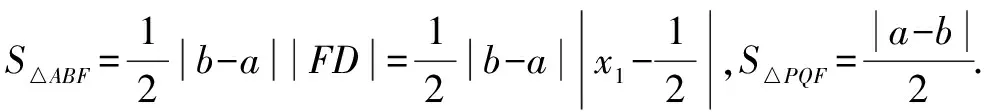
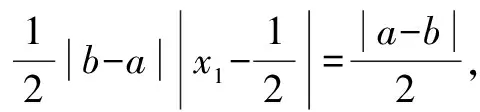
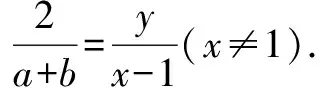
四、定值(定点、定直线)问题
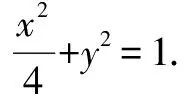
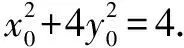
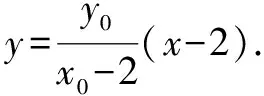
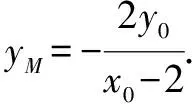
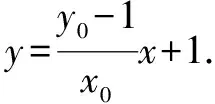
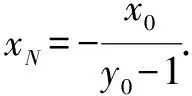
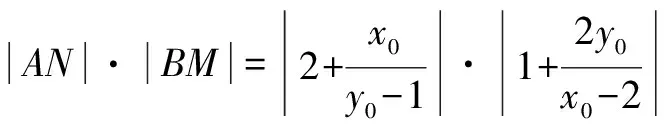
五、参数取值范围问题
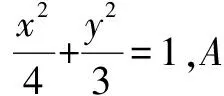
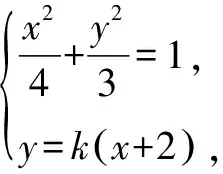
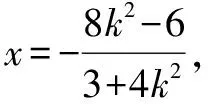
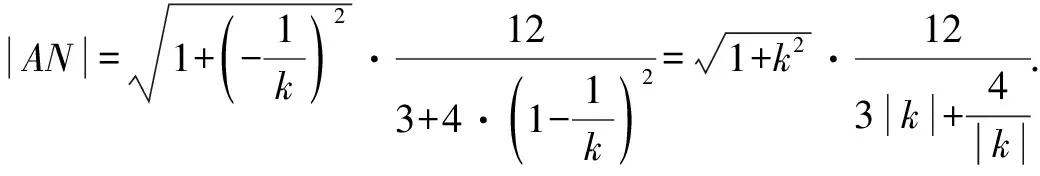
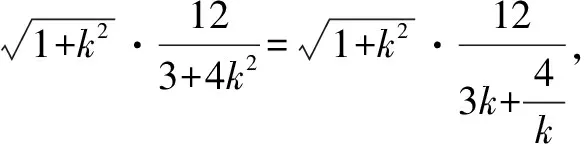
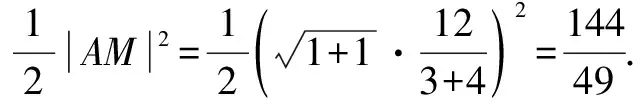
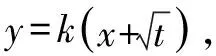
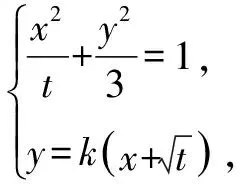
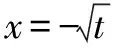
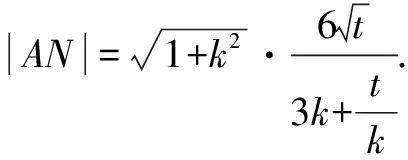
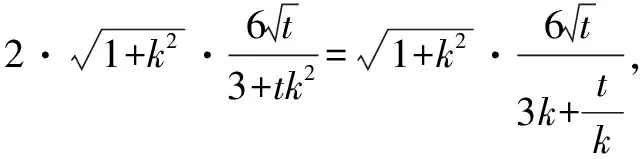
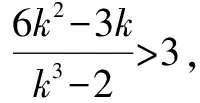
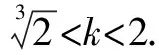
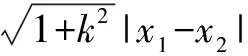
六、对称问题
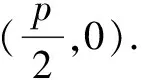
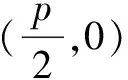
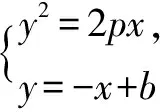
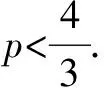
七、存在性问题