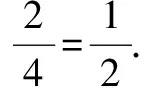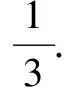例说如何利用列举基本事件求解古典概率

刘玉成 陈国林

(1.安徽省利辛高级中学236700；2.江西省东华理工大学 330000)

在求解古典概率试题中，列举基本事件的方法是最为常见也是最为好用的一种方法，下面就一起来赏析以下试题，然后进行归纳.

例题1 (2016山东滨州二模)一个盒子里装有标号为1,2,3,4,5,6,7,8,9的9张标签，随机地选取7张标签，则取出的7张标签的标号的平均数是5的概率为( ).

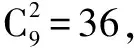
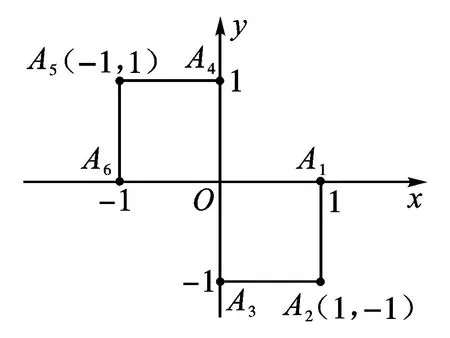
例题2 (2013年江西卷)小波以游戏方式决定是去打球、唱歌还是去下棋．游戏规则为：以O为起点，再从A1，A2，A3，A4，A5，A6(如图)这6个点中任取两点分别为终点得到两个向量，记这两个向量的数量积为X，若X>0就去打球，若X=0就去唱歌，若X<0就去下棋．

(1)写出数量积X的所有可能取值；

(2)分别求小波去下棋的概率和不去唱歌的概率．

解析 (1)X的所有可能取值为-2，-1，0，1.

故所有可能的情况共有15种．

例题3 (黑龙江哈尔滨第六中学2015届高三下学期第四次模拟文7)某种饮料每箱装6听，如果其中有2听不合格，问质检人员从中随机抽出2听，检测出不合格产品的概率为( ).

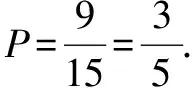
例题4 (2014年湖北卷)随机掷两枚质地均匀的骰子，它们向上的点数之和不超过5的概率记为p1，点数之和大于5的概率记为p2，点数之和为偶数的概率记为p3，则( ).

A．p1

C．p1

例题5 (云南省2015届高三第一次复习统测数学文11)在2,0,1,5这组数据中，随机取出三个不同的数，则数字2是取出的三个不同数的中位数的概率为( ).

例题6 (2014年浙江卷)在3张奖券中有一、二等奖各1张，另1张无奖．甲、乙两人各抽取1张，两人都中奖的概率是____．

归纳总结：有关古典概率的考题都具有创新性，立意新颖的特点．在求解古典概率中如果所求事件对应的基本事件规律性不强，不易求解，一般情况下都可以通过列举基本事件，再求概率．列举的关键是要有规律性方可列举，从而确保不重不漏．如果在问题求解过程中基本事件较多，应注意对立事件概率公式的应用．