垦利油田高黏原油掺稀黏度变化规律
曲兆光 刘春雨 万宇飞 王文光 唐宁依 黄岩
中海石油(中国)有限公司天津分公司
据统计,渤海高黏原油储量达27.3×108m3,占渤海油气资源总储量的68%。目前,渤海稠油动用储量极低,随着渤海常规原油的不断开发,稠油作为一种特殊资源,将在渤海油田的上产增产方面发挥更加重要作用。比如,目前正在大力开发的垦利9-5/9-6油田、旅大5-2北油田、垦利9-1油田、旅大21-2油田、金县1-1油田和绥中36-1油田等所产原油均为稠油,其中不乏黏度极高的特稠油和超稠油。
在海上油田前期研究阶段,面对众多的工程方案和输送方案,需要对各种原油进行掺混输送,若每个方案均开展试验,将造成不必要的浪费,更重要的是实验的进度将跟不上工程方案研究的进度,影响项目的推进。因此,为了更好地开展研究,需要对不同油品掺混后的黏温特性进行预测,以指导工程方案的制定。
针对油品混合后黏度的预测,国内外学者通过实验数据回归或半理论推导提出过很多经验、半经验公式或计算图表,但是目前还没有一个普适模型,每个模型都有一定的工作范围。而高黏油品的掺混,特别是黏度比相差很大的高黏油掺混则更为复杂[1]。当前,常见的做法是对各油田油品分别评估现存模型的适用性,或对现存模型进行修正以符合各油田油品的掺混预测[2]。
1 混合原油黏度预测模型
H.C.库尔纳柯夫于1900年提出,在室温以上温度下,液态烃产品与其他非极性组分混合物的黏度与组分黏度之间的关系呈非线性变化,其混合油黏度可以通过组分油黏度的不同函数的线性加和来表达,如式(1)。
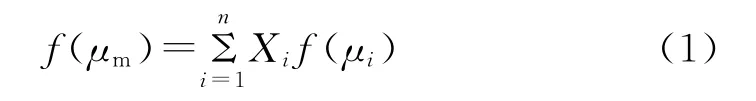
式中:μm为混合油黏度,mPa·s;μi为组分油i的黏度,m Pa·s;Xi为组分油i的质量分数,ΣXi=1;f(μm)、f(μi)为混合油、组分油黏度的函数。
由于各地油品性质、组分、密度等不同,难以找到一种普适的油品掺混黏度预测模型[3],于是一些学者在大量实验或半理论的基础上,对现存的一些模型进行修正,如利用两种组分原油各占一半的混合原油黏度为基础进行修正而得到一些新的模型。根据黏度的函数形式不同,大体上可分为以下4类模型。
1.1 基于理想溶液的烃类混合物黏度预测模型
这类模型主要是基于纯烃混合物理想溶液和热力学性质的混合规律得到,虽然仅适用于烃类物质掺混的黏度预测,但为后续各类计算模型的出现提供参考。
1.1.1 Binham模型
1932年,Binham提出黏度的倒数具有加和性,并经过实验验证,如式(2)。可以看出,该模型预测精度会随着组分油品的黏度比增大而显著降低,特别不适合两种组分油黏度相差大的油品混合后黏度的预测[4]。1992年,李闯文通过13组实验结果对该模型进行预测,发现结果并不理想,在此基础上提出一种改进模型,如式(3)。
Binham:

Binham修正:

式中:μm为混合油黏度,m Pa·s;μi为组分油i的黏度,mPa·s;Xi为组分油i的质量分数,ΣXi=1,i=1~n;Bjk、Cjk为考虑组分油间相互关系的常数。
1.1.2 Arrhenius模型
1887年,Arrhenius首次提出烃类混合物的黏度预测计算式,如式(4)。在该模型的基础上,大量学者基于实验结果的分析和处理,提出相应的修正模型和演化模型[5],其中典型的修正模型主要有3种:式(5)是在Arrhenius模型的基础上考虑了组分油之间的相互作用而引入常数C12值,该改进模型又称为Grunberg-Nisson模型;式(6)~式(7)的修正是在Grunberg-Nisson模型的基础上通过实验拟合后引进系数B12,对组分油间相互作用的进一步修正[6],分别称之为Arrhenius修正1、Arrhenius修正2模型。
Arrhenius:
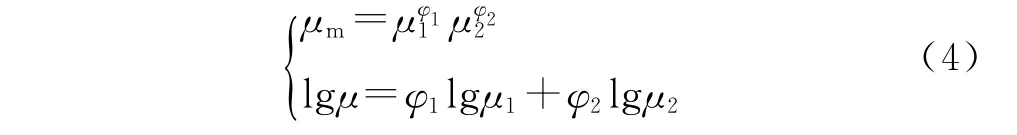
Grunberg-Nissoon:

Arrhenius修正1:
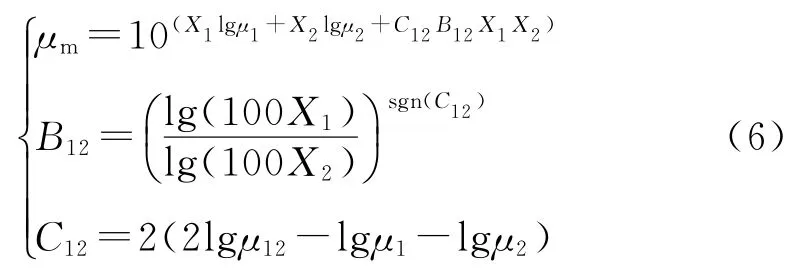
Arrhenius修正2:

式中:μm为混合油黏度,m Pa·s;μ1、μ2为组分油黏度,m Pa·s;φ1、φ2为组分油体积分数;X1、X2为组分油质量分数;B12、C12为考虑组分油间相互关系的常数。
1.1.3 Kendal-Monroe模型
以上两种模型均不适合组分油黏度相差较大的情况,于是Kendal和Monroe对黏度相差较大的溶液进行实验和分析,提出一种立方根加和性模型[7],如式(8)。据API报道[8],有学者曾利用1300组混合油测试结果对该模型进行评价,结果显示平均误差仅为5.7%,预测效果明显。
Kendal-Monroe:
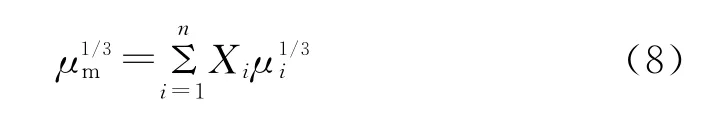
式中:μm为混合油黏度,mPa·s;μi为组分油i黏度,m Pa·s;Xi为组分油i质量分数,ΣXi=1,i=1~n。
1.2 双对数模型
双对数模型是在稠油掺稀降黏实验数据的基础上,发现在“质量分数-黏度双对数”坐标轴上组分油与混合油点之间呈线性分布[9],如式(9)。该模型不适用于黏度指数相差较大和非牛顿混合油。为此,李闯文等利用新疆稠油进行实验,引入相关参量,提高了双对数模型的计算精度并克服不适用于非牛顿流体的特性,即双对数修正1模型[10],又叫李闯文模型,如式(10)。刘天佑等利用黏度差异较大的组分油进行实验,引入表征组分油物性和掺混条件的参量而对双对数模型修正,提出另外一种双对数修正2模型,又叫刘天佑模型[11],如式(11)。辽河油田和新疆油田部分区块掺稀稠油黏度预测符合双对数模型[12-14]。
双对数:

双对数修正1:

双对数修正2:

式中:μm为混合油黏度,m Pa·s;μi为组分油i黏度,mPa·s;Xi为组分油i质量分数,ΣXi=1,i=1~n;Bjk、Cjk为考虑组分油间相互关系的常数。
1.3 Cragoe模型
1933年,Cragoe基于大量油品掺混测试实验结果,提出表征油品流动能力的流函数L,并与油品黏度相关联[15],从而创造性地提出一种新的油品掺混黏度计算模型,如式(12)。据报道,该模型适用范围较广泛,可用于黏度比大于1000的情况[16]。
Cragoe:
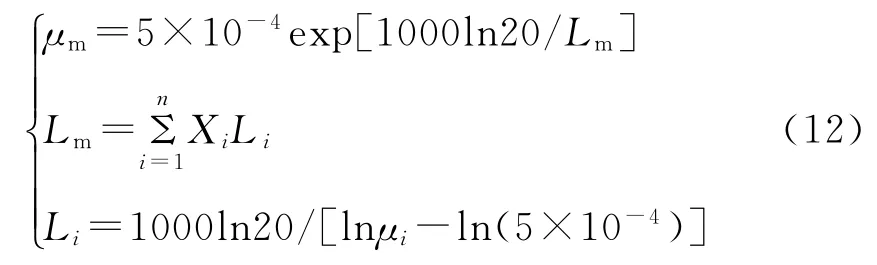
Cragoe修正:
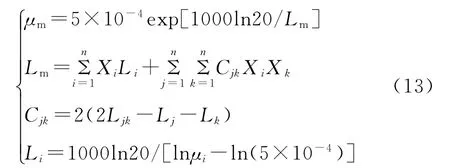
式中:μm为混合油黏度,mPa·s;μi为组分油i黏度,m Pa·s;Xi为组分油i质量分数,ΣXi=1,i=1~n;Lm、Li分别为混合油和组分油i流函数;Cjk为考虑组分油间相互关系的常数。
自该模型提出后,在许多油品的掺混中得到很好的预测效果,但也有一些油品预测精度不容乐观,于是许多学者提出较多的修正模型,其中效果较好的包括中国石油大学类比油品掺混凝点变化规律,得到Cragoe修正模型,如式(13)。据报道,该模型对1577个黏度点进行分析,发现牛顿流体黏度的计算偏差仅为7.2%,非牛顿流体黏度预测偏差为19.1%,预测精度满足工程应用要求[17]。万宇飞等[18]利用新疆风城特稠油和柴油实验结果反算出C值用于其他掺混比和温度点的黏度预测,并取得理想结果。
1.4 Lederer模型与Shu模型
Lederer模型是基于Arrhenius模型演化而来,如式(14)。有学者利用黏度相差较大的油品掺混对该模型进行验证,发现该模型特别适合于黏度比大的场合,甚至黏度比在103~108范围内仍具备较高的预测精度[19-20]。还有文献表明,该模型适用于多相流动场合[21-23],但该模型的经验常数α是通过一定的黏度数据拟合而来,所以应用起来较为局限。印度学者Shu研究发现α(α=0~1)与组分油密度、黏度三者之间的关系式,从而使改进后的Lederer模型(又叫Shu模型,如式(15))在应用范围和预测精度上均有较大的提高[24-25]。
Lederer:

Shu:

式中:μm为混合油黏度,mPa·s;μA、μB为组分油黏度,mPa·s;XA、XB为组分油质量分数;α为经验常数;δA、δB、△δ分别为组分油 A、B的密度和密度差,kg/m3。
2 模型计算与比较
垦利油田群位于渤海南部海域,经多年开发,周边已建立多座平台和相应的海底管线。新油田在开发研究过程中需对周边各种依托可能性进行研究,即该稠油与周边各油田油品掺混后外输至FPSO或陆上终端储存。这就需要对各种方案开展实验,研究掺混不同油品的黏温特性。若一一开始实验,会严重影响油田的开发进程,造成不必要的人力和财力浪费。其可行的方法是研究该油田原油掺混黏度相关规律,通过计算预测掺混后黏度数据,用于依托海管的计算。
2.1 基础数据
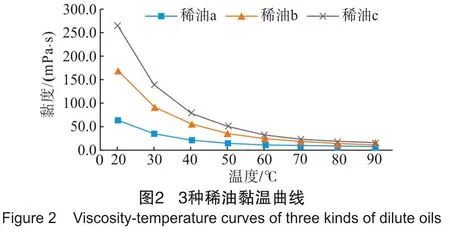
垦利油田群中某待开发油田A所产原油黏度较高,50℃下黏度为2700 mPa·s,拟采用依托周边油田开发。选取周边可能被依托开发的3个不同黏度梯队的稀油油田原油(称为稀油a、稀油b和稀油c)作为组分油。按照各油田产油量配比,分别与垦利油田A原油掺混,利用HAAKE MARS高温高压流变仪及配套温控器对混合原油进行测量,各组分油黏温特性如图1~图2所示。

2.2 不同模型预测结果与偏差
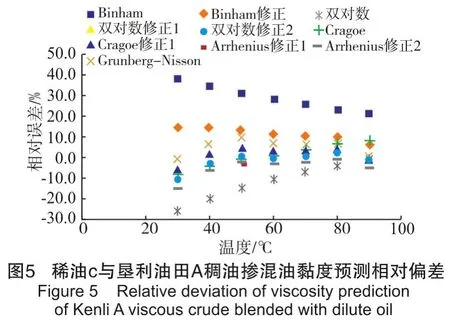
分别利用上文提到的各模型对目标油品掺混后的黏度进行预测,并将预测结果与实测值相比较,评估各模型的预测效果,结果如图3~图5所示。值得注意的是,由于部分模型预测偏差较大,甚至超过100%,图3~图5中仅显示预测偏差相对较小的模型结果。其中,定义相对偏差RD=100%×(实测值-预测值)/实测值,平均相对偏差
从图3~图5可以看出:①各模型预测效果随温度升高而提高,绝大多数模型在低温时,预测相对偏差超过20%,不能满足工程计算的需要;②各模型对于不同油品掺混后黏度预测表现出不同的效果,需要对多组油品的掺混黏度进行评价;③各模型中修正模型的预测精度一般高于原始模型,说明修正模型中引入的系数在一定程度上能够反映不同地区的油品特征;④对于稀油a与垦利油田A稠油掺混后黏度预测来说,Arrhenius修正2、Cragoe修正和双对数修正1模型预测效果较好;对于稀油b与垦利油田A稠油掺混后黏度预测来说,双对数修正1、双对数修正2、Cragoe、Cragoe修正、Arrhenius修正1、Arrhenius修正2和Grunberg-Nisson模型预测精度较高;对于稀油c与垦利油田A稠油掺混后黏度预测来说,双对数修正2、Cragoe修正、Arrhenius修正1和Arrhenius修正2模型预测能力能够满足工程实际需要。


将各模型对3种稀油分别与垦利油田A稠油掺混后黏度预测结果的相对偏差取平均值,得到各模型预测的平均相对偏差(见表1)。从表1可看出,Cragoe修正模型和Arrhenius修正2模型在3种油品的掺混下均表现出较高的预测精度,从工程的角度来说,均可以满足实际需要。但评价一个模型时,希望模型具有较好的预测稳定性,即平均相对偏差对不同油品预测精度变化幅度较小,从Cragoe修正模型和Arrhenius修正2模型来看,Arrhenius修正2模型平均相对偏差范围为4.72%~6.21%,小于Cragoe修正模型的3.43%~8.75%,即Arrhenius修正2模型预测稳定性较强。综上所述,推荐Arrhenius修正2模型作为垦利油田A稠油与周边稀油掺混后黏度预测的模型。
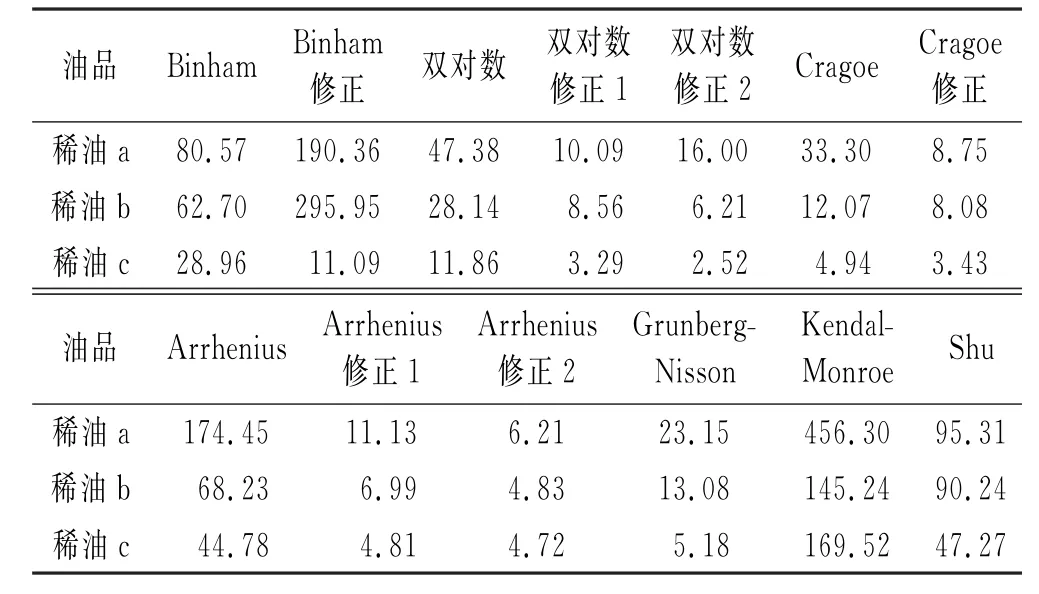
表1 各稀油与垦利油田A稠油掺混油黏度预测平均相对偏差Table 1 Average relative deviation of viscosity prediction of Kenli viscous crude-solvent mixtures %
3 结论
在海上油田依托式开发研究过程中,需要对周边各种油品掺混外输方案进行研究,从研究效率和经济性角度来说,寻找一种适合于本油田的黏度预测模型较一一开展掺混实验更加可取。首先调研了国内外油品掺混黏度预测模型,然后以渤海垦利油田群中新开发稠油油田原油为基础,掺混周围可能的3种稀油进行预测,并将预测结果与实验值进行比较分析,认为:
(1)常见典型的混合油黏度预测模型中,相关常数(如Cragoe中C值,Lederer中α值)表征原油性质,对于不同地区或组分相差较大的原油应有所区别。
(2)各修正模型主要考虑了组分油之间的相互关系,使得其预测精度较原始模型高,在本研究中得到一定程度的验证。
(3)各模型对垦利油田A稠油与3种稀油掺混后的黏度预测效果普遍随温度的降低而恶化,在较高温度下预测精度相对较高。
(4)Cragoe修正模型和Arrhenius修正2模型对目标油品的掺混均有较高的预测精度,能满足工程实际的需要。
(5)综合考虑预测精度和预测稳定性,推荐Arrhenius修正2模型作为垦利油田A稠油与周边稀油掺混后黏度的预测模型。

